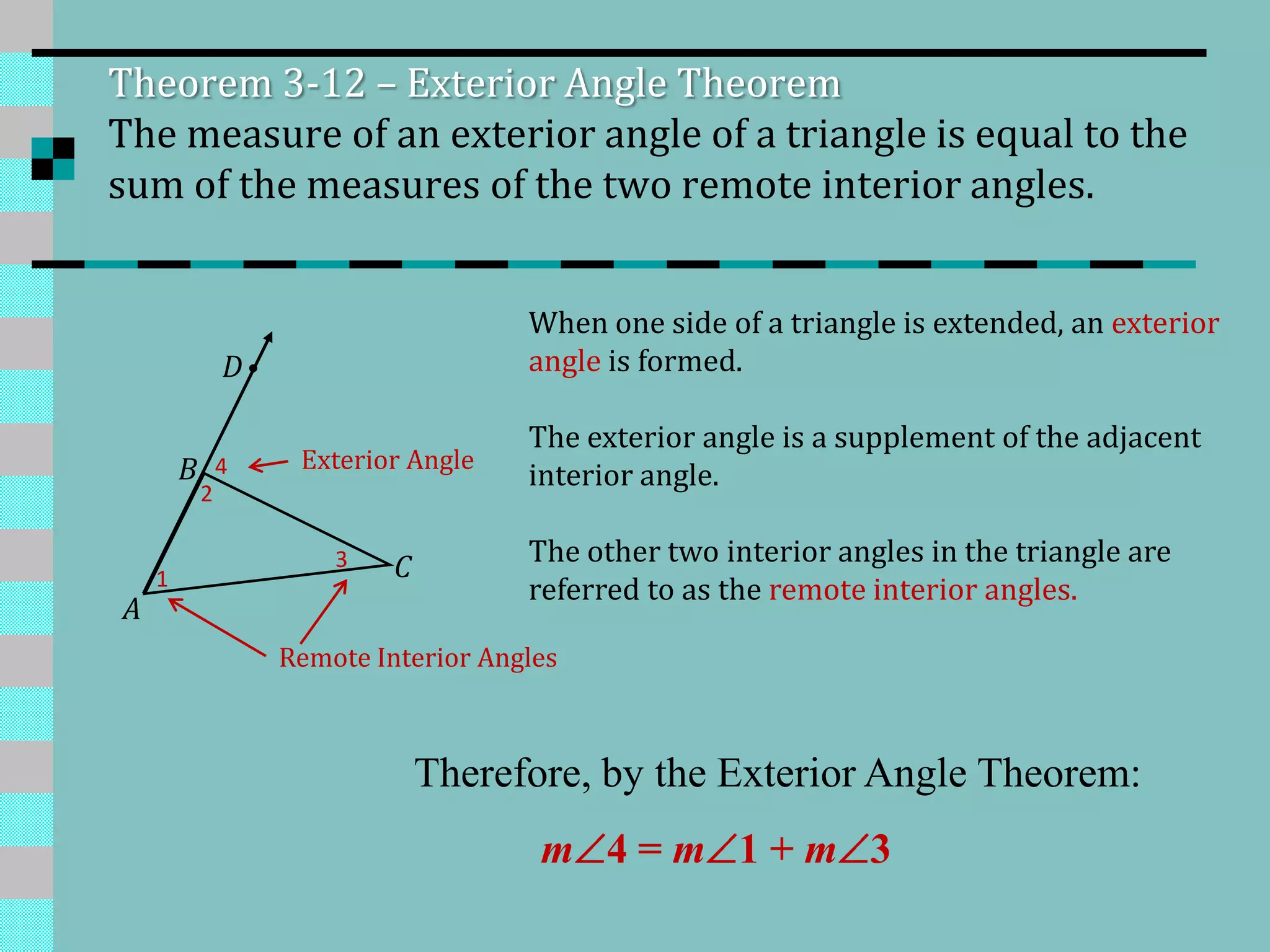
This document discusses triangles and their properties. It defines different types of triangles based on their sides and angles. The three main points are: 1) The sum of the measures of the angles of any triangle is 180 degrees. 2) There are several corollaries that follow from the fact that triangle angles sum to 180 degrees, such as if two angles are congruent the third must also be congruent. 3) The Exterior Angle Theorem states that the measure of an exterior angle of a triangle equals the sum of the remote interior angles.

1. Applying Parallel Lines to
Polygons
Section 3-4
Angles of a Triangle
Review of Major Points

2. Triangle definition: the figure formed by
three segments joining three noncollinear
points.
A
B
C
Triangle ABC ( ABC)
Vertices of ABC: points A, B, C
Sides of ABC:
Angles of ABC: A, B, C
, ,AB BC CA

3. Classifying Triangles
By the number of
congruent sides it has.
Scalene triangle:
No sides
Isosceles triangle:
At least two sides
Equilateral triangle:
All sides
By their angles.
Acute triangle:
Three acute angles
Obtuse triangle:
One obtuse angle
Right triangle:
One right angle
Equiangular triangle:
All angles

4. Theorem 3-11
The sum of the measures of the angles of a triangle is 180.
Corollaries from the theorem: A statement that can be proved easily by applying a
theorem is called a corollary.
• Corollary 1
• If two angles of one triangle are congruent to two angles of another triangle, then the
third angles are congruent.
• Corollary 2
• Each angle of an equiangular triangle has measure 60.
• Corollary 3
• In a triangle, there can be at most one right angle or obtuse angle.
• Corollary 4
• The acute angles of a right triangle are complementary.

5. A
B
C1
2
3
4
D
Theorem 3-12 – Exterior Angle Theorem
The measure of an exterior angle of a triangle is equal to the
sum of the measures of the two remote interior angles.
When one side of a triangle is extended, an exterior
angle is formed.
The exterior angle is a supplement of the adjacent
interior angle.
The other two interior angles in the triangle are
referred to as the remote interior angles.
Exterior Angle
Remote Interior Angles
Therefore, by the Exterior Angle Theorem:
m 4 = m 1 + m 3