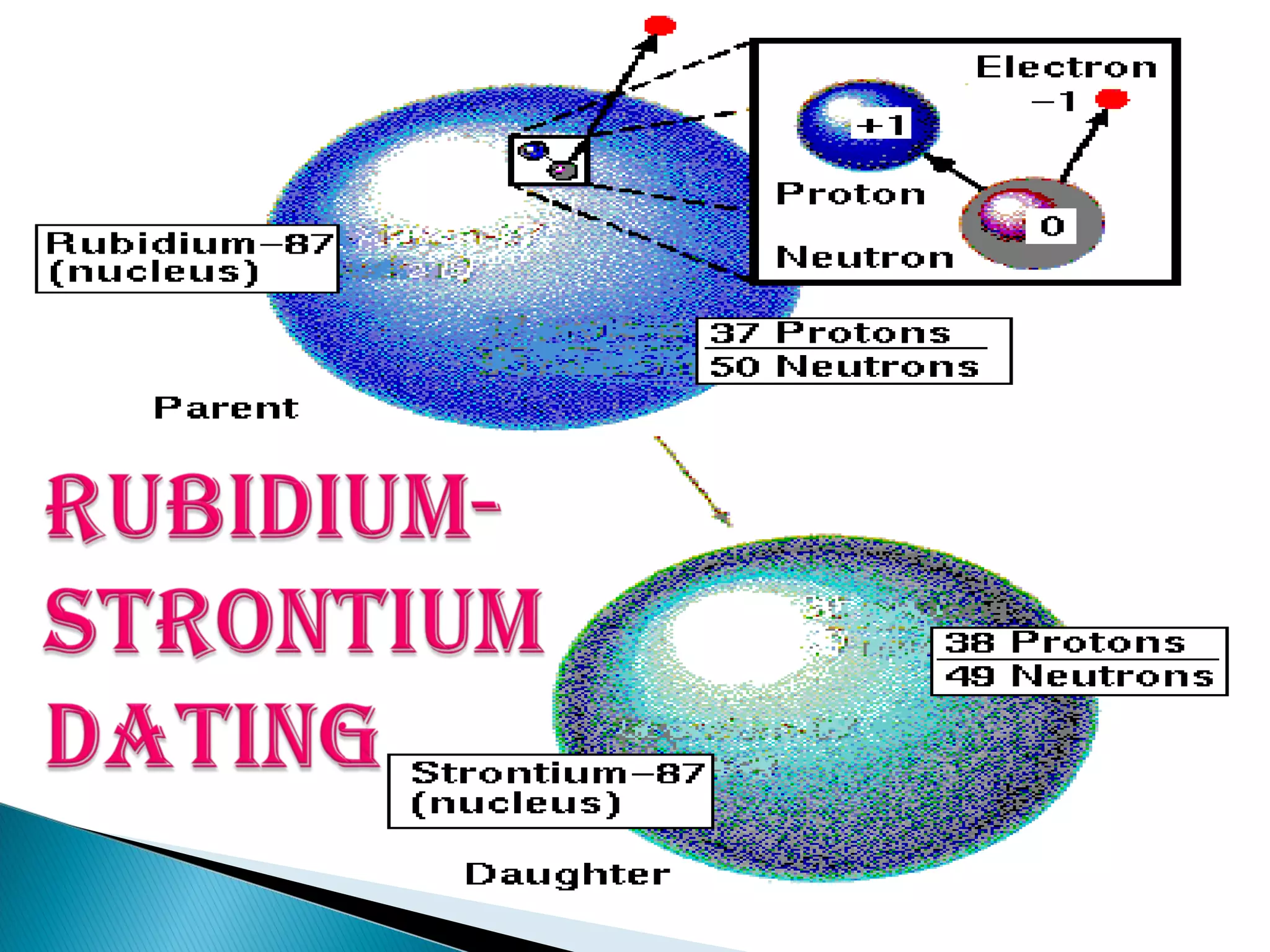
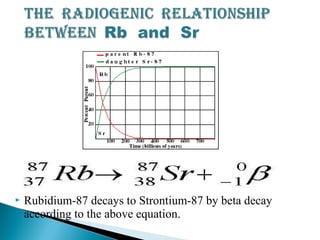
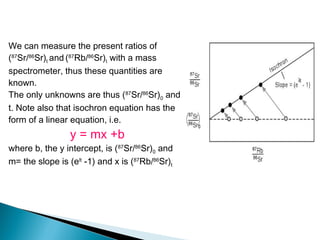
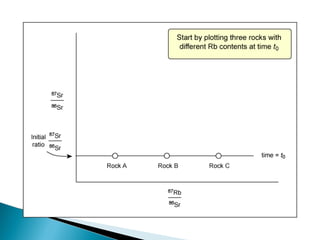
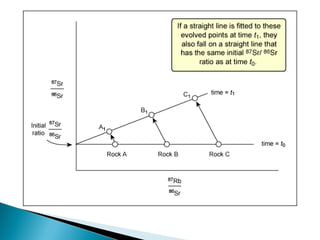
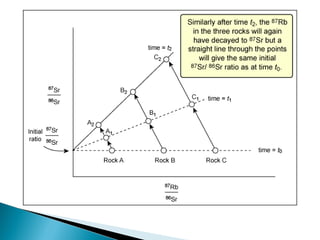
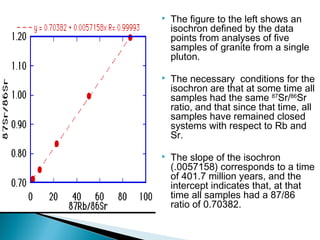
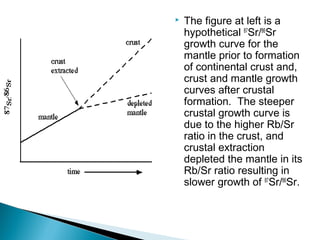
The Rb-Sr dating method uses the radioactive decay of rubidium-87 to strontium-87 to date rocks and minerals. It works by measuring the ratio of rubidium to strontium, and the ratio of radiogenic strontium-87 to strontium-86, in samples. By plotting these ratios on a graph called an isochron, scientists can determine the age of the sample from the slope of the line. The method relies on the samples forming a closed system and not being altered after formation. It is useful for determining the age of igneous and metamorphic rocks.

2. 1. Introduction
2.History
3.Chemical properties
4.Nuclear properties
5.Importance of Rb-Sr dating
6.Methodology for dating
7.Source of Rb-Sr
8.Isochron equation
9.Sources of error/ limitations
10.Uses
11.Reference

3.  The rubidium-strontium dating method is a
radiometric dating technique used by scientists to
determine the age of rocks and minerals from the
quantities they contain of specific isotopes of
rubidium (87Rb) and strontium ( 87Sr, 86Sr).

4.  Development of this process was aided by
German chemist Fritz Strassmann, who later went
on to discover nuclear fission with German
chemist Otto Hahn and Swedish physicist
Lise Meitner.

5. Rubidium Strontium
 Alkali element (group I)  Alkaline earth element
 +1 valency (group II A)
 Ionic radii 1.48 angstrom  +2 valency
which is close to “K” so it  Ionic radii 1.13 angstrom
substitute for K e.g. in K- which is close to Ca, so
feldspar and mica. Sr can replace it in Ca
 More incompatible containing minerals like in
 Its concentration is high plagioclase and CPX.
in crust then in mental.  Less incompatible than
Rb
 Its concentration in crust
is less than Rb.

7. Rb is a highly incompatible element. Sr is fairly
incompatible.
This means that as partial melting occurs, Rb is
going to partition to the melt in greater proportion
than Sr will.
From this partitioning, the mantle will become
depleted in Rb relative to Sr and is called
depleted mantle.
Concurrently, the crust will become enriched in Rb
relative to Sr.

8. Atomic mass no. Rubidium Strontium
abundance(%) abundance(%)
84 ------------------ 0.56 (stable)
85 72.12 (stable) -----------------
86 ------------------- 9.87 (most stable)
87 27.83 (unstable) 7.00 (stable)
88 ------------------- 82.57 (stable)

9.  The element rubidium consists of two isotopes
having atomic mass numbers of 85 (72.16%) and
87 (27.84%).
 Rb decays to 87Sr by a weak b- emission. The
decay constant is :- l = 1.42 x 10-11 /yr.

10.  Rubidium-87 decays to Strontium-87 by beta decay
according to the above equation.

11.  The amount of 87Sr found in a sample at any time
is determined by:-
1. the decay constant of 87Rb,
2. the initial amount of 87Sr in the sample,
3. the time since the initial time and the ratio of Rb
to Sr in the system.
4. This can be seen in the equation below.
Where lambda is the decay constant and t is the age of the
system.

12.  The utility of the rubidium-strontium isotope
system results from the fact that :-
• 87Rb (one of two naturally occurring isotopes of
rubidium) decays to 87Sr with a half-life of 48.8 billion
years.
• Rb is a highly incompatible element that, during
fractional crystallization of the mantle, stays in the
magmatic melt rather than becoming part of mantle
minerals.
• The radiogenic daughter, 87Sr, is produced in this decay
process and was produced in the original primordial
nucleosynthesis of the universe.

13.  Different minerals gives different ratios of
radiogenic strontium-87 to naturally occurring
strontium-86 (87Sr/86Sr) through time; and their
age can be calculated by:-
1. measuring the 87Sr/86Sr in a mass spectrometer,
2. knowing the amount of 87Sr present when the
rock or mineral formed,
3. and calculating the amount of 87Rb from a
measurement of the Rb present
4. and knowledge of the 85Rb/87Rb weight ratio.

14.  Ifthese minerals crystallized from the
same silicic melt, each mineral had the
same initial 87Sr/86Sr as the parent melt.
However, because Rb substitutes for K in
minerals and these minerals have different
K/Ca ratios, the minerals will have had
different Rb/Sr ratios.

15.  During fractional crystallization, Sr tends to become
concentrated in plagioclase, leaving Rb in the liquid
phase.
 Hence, the Rb/Sr ratio in residual magma may increase
over time, resulting in rocks with increasing Rb/Sr ratios
with increasing differentiation.
 Typically, Rb/Sr increases in the order:- plagioclase,
hornblende, K-feldspar, biotite, muscovite.
 Therefore, given sufficient time for significant
production (ingrowth) of radiogenic 87Sr, measured
87
Sr/86Sr values will be different in the minerals,
increasing in the same order.

16.  Consider the case of an igneous rock such as a granite
that contains several major Sr-bearing minerals
including plagioclase feldspar, K-feldspar, hornblende,
biotite, and muscovite.
 Each of these minerals has a different initial
rubidium/strontium ratio dependent on their potassium
content, the concentration of Rb and K in the melt and
the temperature at which the minerals formed.
 Rubidium substitutes for potassium within the lattice of
minerals at a rate proportional to its concentration within
the melt.

17.  The ideal scenario according to Bowen's reaction series
would see a granite melt begin crystallizing a cumulate
assemblage of plagioclase and hornblende (i.e.; tonalite
or diorite), which is low in K (and hence Rb) but high in
Sr (as this substitutes for Ca), which proportionally
enriches the melt in K and Rb.
 This then causes orthoclase and biotite, both K rich
minerals into which Rb can substitute, to precipitate.
 The resulting Rb-Sr ratios and Rb and Sr abundances of
both the whole rocks and their component minerals will
be markedly different.
 This, thus, allows a different rate of radiogenic Sr to
evolve in the separate rocks and their component
minerals as time progresses.

18.  The age of a sample is determined by analyzing
several minerals within the sample.
 The 87Sr/86Sr ratio for each sample is plotted against
its 87Rb/86Sr ratio on a graph called an isochron .
 If these form a straight line then the samples are
consistent, and the age probably reliable.
 The slope of the line dictates the age of the sample.

19.  87Rb decays to 87Sr* by b decay. The neutron emits
an electron to become a proton.
 For this decay reaction, l = 1.42 x 10-11 /yr, t = 4.8
1/2
x 1010 yr
 At present, 27.85% of natural Rb is 87Rb.
 If we use this system to plug into equation, D* =
Nelt-N = N(elt-1)
then, 87Sr* = 87Rb (elt-1) (1.)
but, 87Srt = 87Sr0 + 87Sr*

20. Plugging this into equation (1)
87
Srt = 87Sr0 + 87Rb (elt-1) (2)
We still don't know 87Sr0 , the amount of 87Sr daughter
element initially present.
To account for this, we first note that there is an
isotope of Sr, 86Sr, that is:
(1) non-radiogenic (not produced by another
radioactive decay process),
(2) non-radioactive (does not decay to anything else).
Thus, 86Sr is a stable isotope, and the amount of 86Sr
does not change through time
If we divide equation (2) through by the amount
of 86Sr, then we get:-

21.  ( 87Sr/86Sr) t = ( 87Sr/86Sr ) 0+( 87Rb/ 86Sr) t(elt -1)
 Since, it is a lot easier to measure the ratio of
isotopes in a sample of rock or a mineral, rather
than their absolute abundances. Therefore we
divide the above equation by Sr86
 The above equation is known as “ISOCHRON
EQUATION”.

22. We can measure the present ratios of
(87Sr/86Sr)t and (87Rb/86Sr)t with a mass
spectrometer, thus these quantities are
known.
The only unknowns are thus (87Sr/86Sr)0 and
t. Note also that isochron equation has the
form of a linear equation, i.e.
y = mx +b
where b, the y intercept, is (87Sr/86Sr)0 and
m= the slope is (elt -1) and x is (87Rb/86Sr)t

23. First note that the time t=0 is the time when initial value
of 87Sr/86Sr was the same in every mineral in the rock
(such as at the time of crystallization of an igneous rock)
because at magmatic temperature, there will be no
fractionation. So y remains constant and there will be
change in x-axis.
In nature, however, each mineral in the rock is likely to
have a different amount of87Rb. So that each mineral will
also have a different 87Rb/86Sr ratio at the time of
crystallization. It decreases with passage of time
whereas (87Sr/86Sr) increases with time Thus, once the
rock has cooled to the point where diffusion of elements
does not occur, the 87Rb in each mineral will decay
to87Sr, and each mineral will have a different 87Rb
and 87Sr after passage of time.

25. After a passage of time, a new rock is formed and
it will inherit (87Sr/86Sr). Whatever initial (87Sr/86Sr)
was there, that was inherited by arbitrary.
(87Sr/86Sr) will keep on increasing because of the
continuous decay of Rb-87.
Sr will contain both original and inherited along
with radiogenic.

28. 1. After each period of time, the 87Rb in each rock
decays to 87Sr producing a new line.
2. This line is still linear but is steeper than the
previous line.
3. We can use this to tell us two important things
1. The age of the rock
2. The initial 87Sr/86Sr isotope ratio

29.  It tells the source from which this particular rock is
obtained.
 Cut-off limit is 0.706.
 Rock is crustal if >0.706
 Rock is mantle if <0.706

30.  If samples are clustered then we can’t get the
value of isochron.
 There should be large variation between Rb
isotope.
 There should be large spread in Rb/Sr ratio i.e
high and low value.
 If initial ratio is not uniform then also we don’t get
isochron. So, composition of daughter must be
homogenous when a new rock is formed.

31.  Rb and Sr are mobile elements. Any rock which is
slightly altered, these elements will leach out.
 In this case, we get younger age i.e wrong age
than actual age.
 Since basaltic rock has more alteration as
compare to granitic rock so they are not preferred.
 So mostly mantle derived rocks would not
generate a good Rb-Sr isochron.

32.  The figure to the left shows an
isochron defined by the data
points from analyses of five
samples of granite from a single
pluton.
 The necessary conditions for the
isochron are that at some time all
samples had the same 87Sr/86Sr
ratio, and that since that time, all
samples have remained closed
systems with respect to Rb and
Sr.
 The slope of the isochron
(.0057158) corresponds to a time
of 401.7 million years, and the
intercept indicates that, at that
time all samples had a 87/86
ratio of 0.70382.

33.  The figure at left is a
hypothetical 87Sr/86Sr
growth curve for the
mantle prior to formation
of continental crust and,
crust and mantle growth
curves after crustal
formation. The steeper
crustal growth curve is
due to the higher Rb/Sr
ratio in the crust, and
crustal extraction
depleted the mantle in its
Rb/Sr ratio resulting in
slower growth of 87Sr/86Sr.

34.  Rb-Sr dating relies on correctly measuring the Rb-Sr
ratio of a mineral or whole rock sample, plus deriving an
accurate 87Sr/86Sr ratio for the mineral or whole rock
sample.
 Several preconditions must be satisfied before a Rb-Sr
date can be considered as representing the time of
emplacement or formation of a rock.
 The system must have remained closed to Rb and Sr
diffusion from the time at which the rock formed or fell
below the closure temperature i.e the temperature at
which a system has cooled so that there is no longer any
significant diffusion of the daughter isotopes out of the
system and into the external environment (generally
considered to be 650 °C);
 The minerals which are taken from a rock to construct an
isochron must have formed in chemical equilibrium with
one another or in the case of sediments, be deposited at
the same time;

35.  The rock must not have undergone any metasomatism
(i.e. the chemical alteration of
a rock by hydrothermal and other fluids) which could
have disturbed the Rb-Sr system either thermally or
chemically
 One of the major drawbacks of utilizing Rb and Sr to
derive a radiometric date is their relative mobility,
especially in hydrothermal fluids. Rb and Sr are relatively
mobile alkaline elements and as such are relatively
easily moved around by the hot hydrothermal fluids
present during metamorphism.
 Conversely, these fluids may metasomatically alter a
rock, introducing new Rb and Sr into the rock. Rb-Sr can
then be used on the altered mineralogy to date the time
of this alteration, but not the date at which the rock
formed.

36. Uses of
Rb-Sr Dating
Strontium
Isotope
geochronology Isotope
geochemistry
stratigraphy

37. Geochronology
 If the initial amount of Sr is known or can be
extrapolated, the age can be determined by
measurement of the Rb and Sr concentrations and
the 87Sr/86Sr ratio. The dates indicate the true age of
the minerals only if the rocks have not been
subsequently altered.
 The important concept in isotopic tracing is that Sr
derived from any mineral through weathering
reactions will have the same 87Sr/86Sr as the mineral.

38.  Initial 87Sr/86Sr ratios are a useful tool in archaeology,
forensics and paleontology because the 87Sr/86Sr of a
skeleton, sea shell or indeed a clay artifact is directly
comparable to the source rocks upon which it was
formed or upon which the organism lived. Thus, by
measuring the current-day 87Sr/86Sr ratio, the
geological fingerprint of an object or skeleton can be
measured, allowing migration patterns to be
determined.

39.  Strontium isotope stratigraphy relies on recognized
variations in the 87Sr/86Sr ratio of seawater over time. The
application of Sr isotope stratigraphy is generally limited to
carbonate samples for which the Sr seawater curve is well
defined. This is well known for the Cenozoic time-scale
but, due to poorer preservation of carbonate sequences in
the Mesozoic and earlier, it is not completely understood
for older sequences.
 In older sequences diagenetic alteration combined with
greater uncertainties in estimating absolute ages due to
lack of overlap between other geochronometers (for
example U-Th leads to greater uncertainties in the exact
shape of the Sr isotope seawater curve.

40.  Jacobsen S.B., Wills J., Yin Q., 2000. Seawater isotope records, crustal
evolution, tectonics and atmospheric evolution. Proceedings, Seventh Annual
V.M. Goldschmidt Conference, 2000. PDF abstract
 USGS (2004) Resources on Isotopes:Strontium,
http://wwwrcamnl.wr.usgs.gov/isoig/period/sr_iig.html.
 Attendorn, H. -G.; Bowen, Robert (1988). "Rubidium-Strontium Dating". Isotopes
in the Earth Sciences. Springer. pp. 162–165. http://books.google.de/books?
id=k90iAnFereYC&pg=PA162.
 Walther, John Victor (1988 2009). "Rubidium-Strontium Systematics". Essentials
of geochemistry. Jones & Bartlett Learning. pp. 383–385.
http://books.google.de/books?id=cYWNAZbPhMYC&pg=PA383
 ISOTOPE GEOLOGY by ‘CLAUDE.J.ALLEGRE’.. The Cambridge Publication
UNITED KINGDOM.

41. THANK