Download to read offline
Uploaded byCindy Smith
Benchmarking
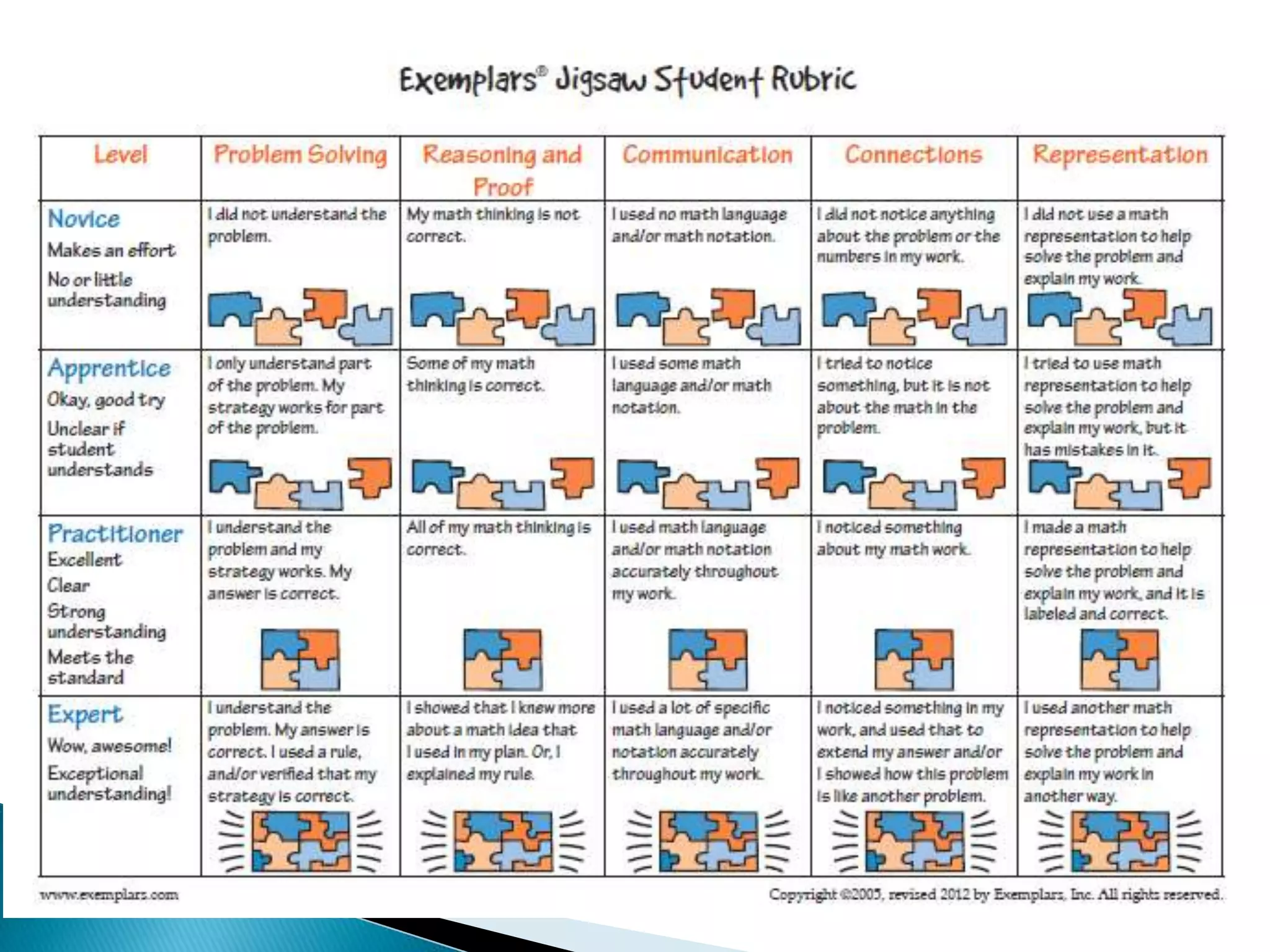
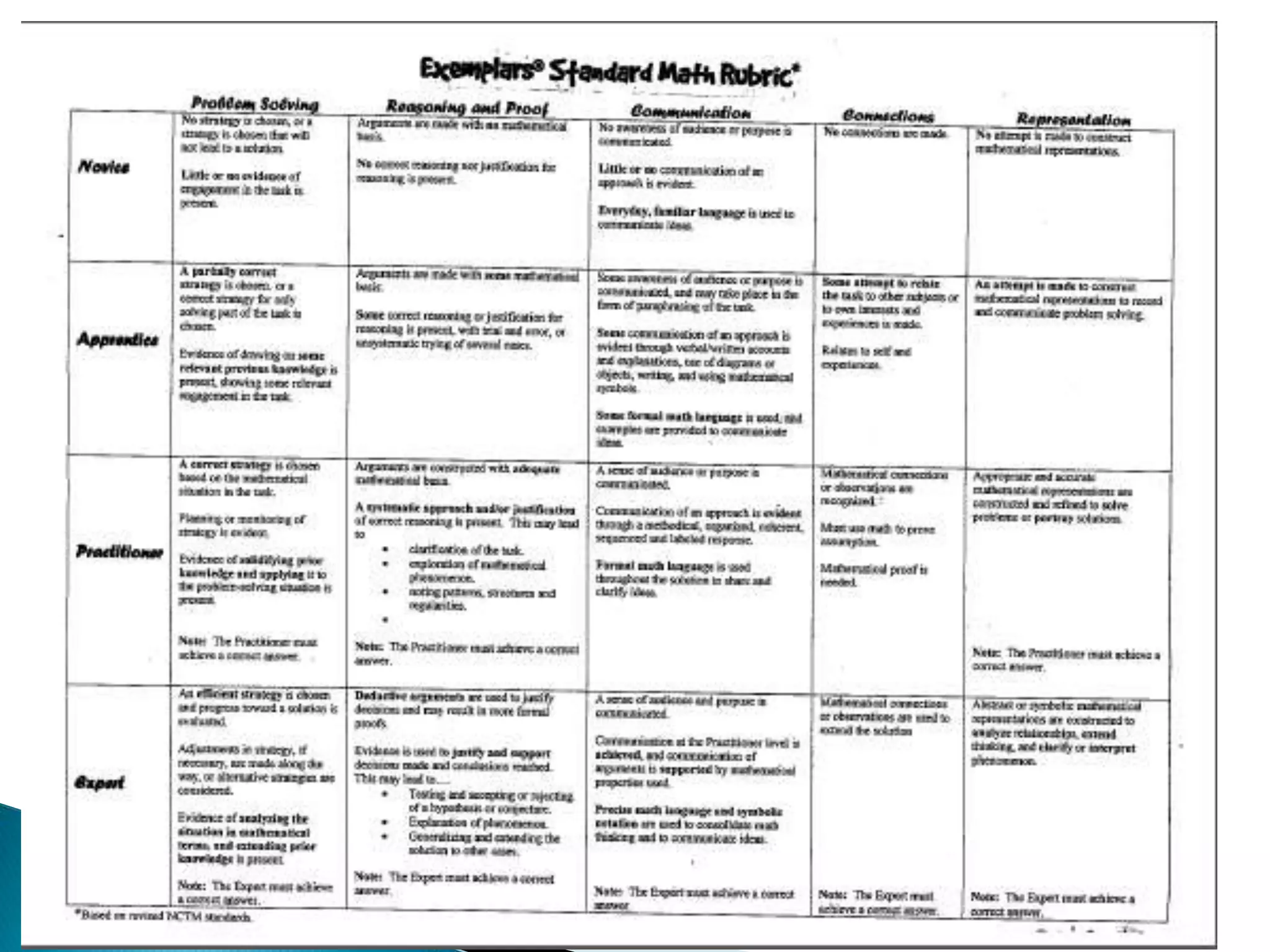
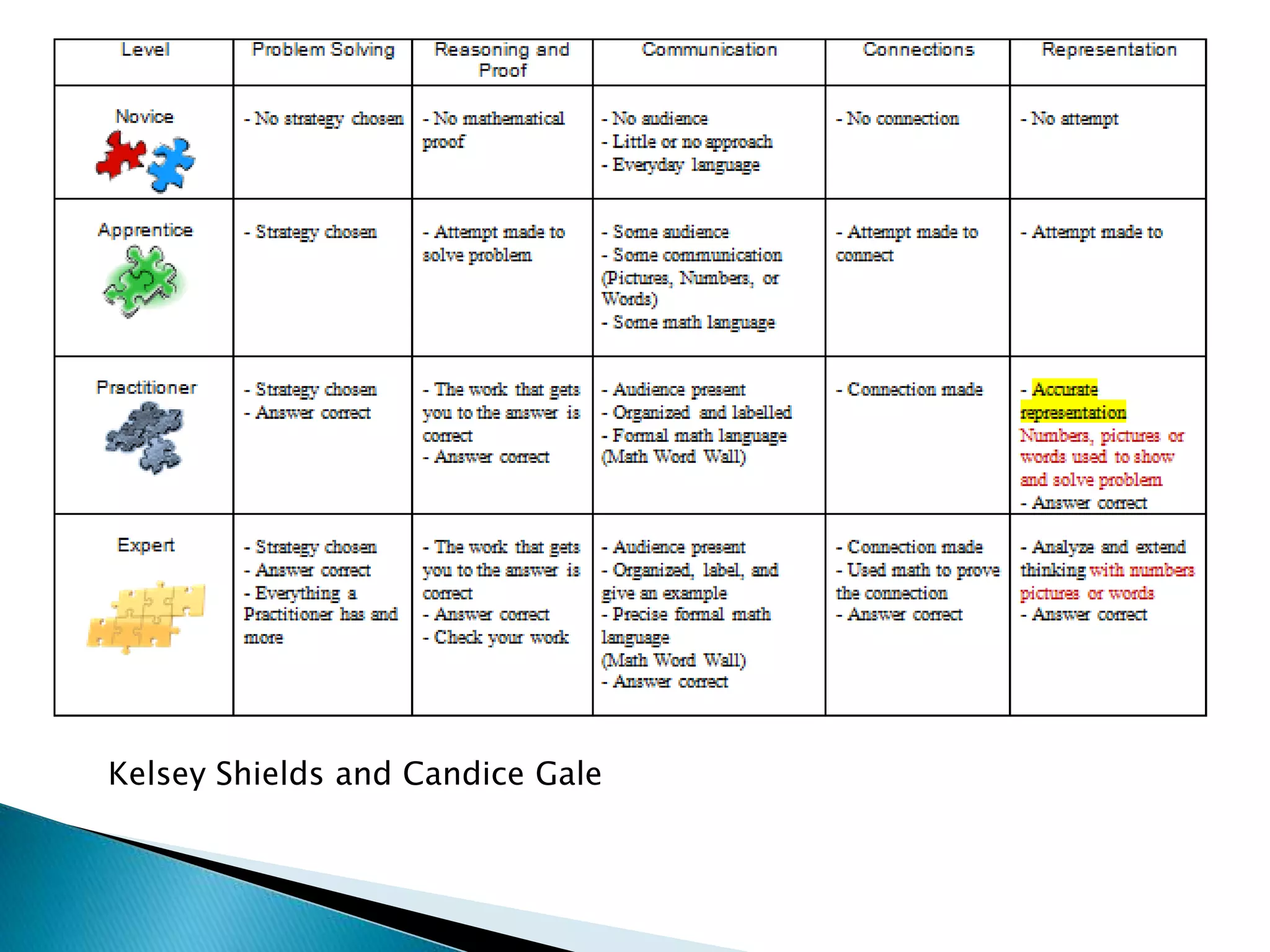
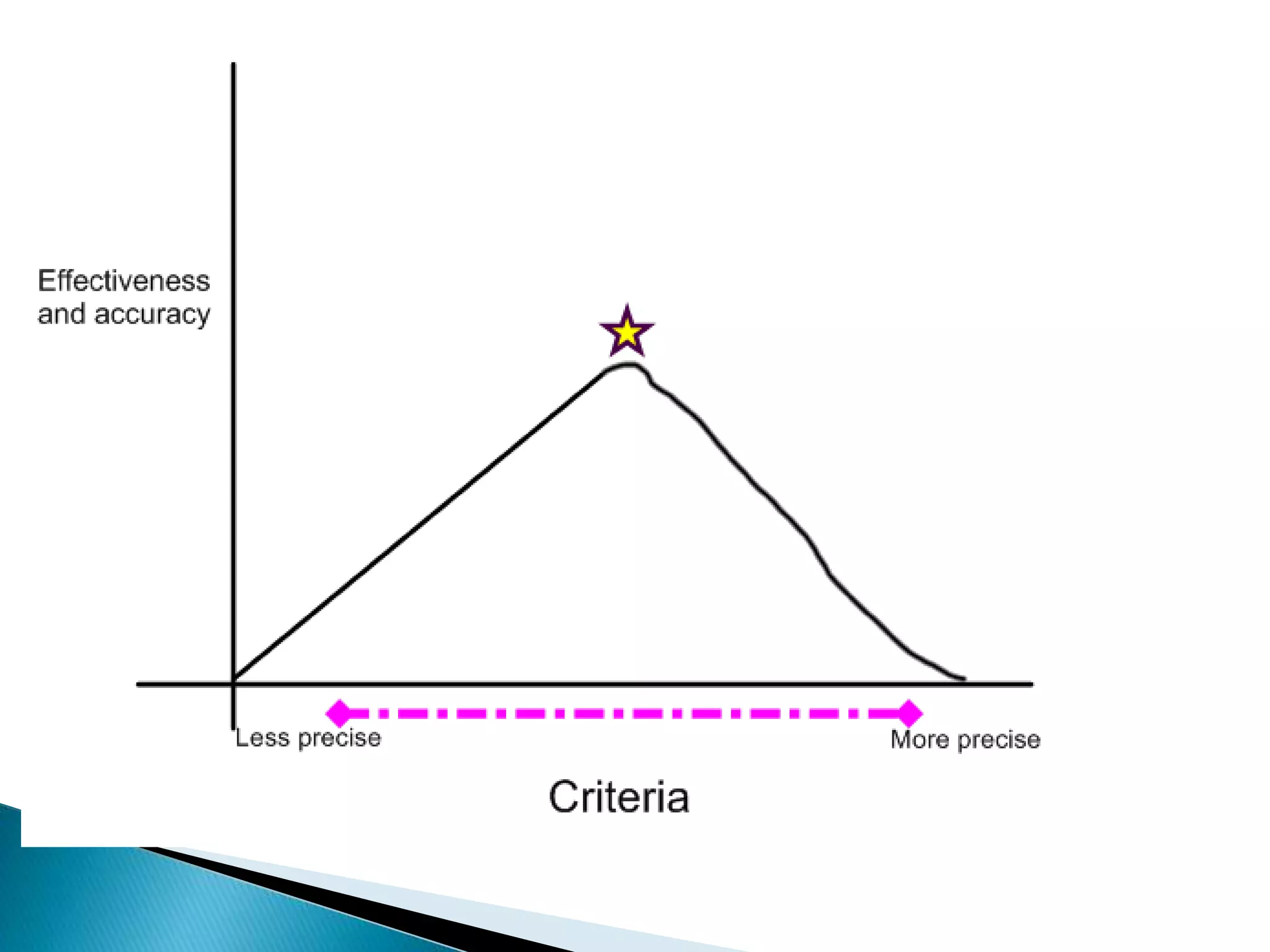
This document discusses the importance of mathematical communication and making connections. It notes that communication allows students to organize their thinking, clarify their understanding to others, and develop new relationships between ideas. When students communicate their mathematical reasoning and thinking, it helps them learn to be clear and persuasive. The document also emphasizes having students recognize and apply mathematics concepts in multiple contexts, as well as using precise language and representations to effectively communicate mathematical arguments.
More Related Content
Benchmarking
- 1.
- 2. Why dowe benchmark? What are the benefits? Challenges? Other points/concerns?
- 6. “One ofthe best and most practical ways to improve accuracy is the collaborative scoring of student work. This is also a superb professional learning experience”
- 7. Kelsey Shields andCandice Gale
- 8. Recognize anduse connections among mathematical ideas Understand how mathematical ideas interconnect and build on one another to produce a coherent whole Recognize and apply mathematics in contexts outside of mathematics NCTM 8
- 9. knowledge isconstructed as the learner strives to organize his or her experiences in terms of pre-existing mental structures or schemes 9
- 10. Math toreal life Math to self Math to Math June 19, 2014 10
- 11. Communication workstogether with reflection to produce new relationships and connections. Students who reflect on what they do and communicate with others about it are in the best position to build useful connections in mathematics. (Hiebert et al., 1997, p. 6) 11
- 12. Organize andconsolidate their mathematical thinking through communication Communicate their mathematical thinking coherently and clearly to peers, teachers, and others Analyze and evaluate the mathematical thinking and strategies of others; Use the language of mathematics to express mathematical ideas precisely. 12
- 13. Through communication,ideas become objects of reflection, refinement, discussion, and amendment. The communication process also helps build meaning and permanence for ideas and makes them public (NCTM, 2000). When students are challenged to think and reason about mathematics and to communicate the results of their thinking to others orally or in writing, they learn to be clear and convincing. Listening to others’ thoughts and explanation about their reasoning gives students the opportunity to develop their own understandings. -Huang June 19, 2014 13
- 14. Tell Me! Describe Explain Justify Debate Convince Proove 14
- 15. "...It becomes evidentto the students and teacher that mathematical communication is not about “answering the question using words, numbers, pictures, and symbols.” Instead, they realize that these forms of communication are selected and applied in order to create a precise mathematical argument, where labelled diagrams and/or numeric expressions and equations are viewed as being more precise, concise and persuasive forms than descriptive narratives. These discussion processes provoke students to use higher-order thinking skills, such as analysis, evaluation and synthesis, in order to improve their conceptual understanding, use of mathematical strategies and mathematical communication."
- 18. We lookfor connections throughout the paper Some problems lend themselves to showcasing different processes and student abilities We decide on what a correct answer looks like We fit the rubric to the problem. Its tricky! We “tighten up” the rubric…but be careful!
- 20. Math toself and real life ◦ “This reminds me of when my Mom made cupcakes for my birthday”, or “Newspapers talk about statistics for sports and money” Math to other subject: “This is like the graphs we did in science” or “we talked about statistics in health class” Math to Math: “ This is a linear relation”. “I could use an equation”. Or “I can make a rule”
- 21. Extending thesolution or problem posing are a type of connection When a student chooses a strategy, creates a representation, discusses the situation in mathematical terms, illustrates, or makes decisions about algorithms, they are really connecting mathematical ideas.
- 22. Introduce writingearly, doesn’t have to be an exemplar Emphasize vocabulary (communication) Discuss strategies, which are efficient Emphasize representations Have students highlight connections they have recognized Emphasize good solid explanations that the reader can follow (logic, reasoning and proof)
- 26.
Editor's Notes
- #3 These are the questions we will be addressing. We will come back to these, because this may be a big conversation! Benchmarking is about changing practice. Overwhelming research about the benefits of teaching math not as piecmeal, rote learning of algorithms and facts, but as connected, applied concepts, through discovery, constructing meaning, connecting schema and dialogue and debate. No doubt about it, it is richer, more meaningful, more lasting learning. This is why we are pushing to change practice in our math instruction. See curriculum and Glanfeild book re: Mathematical Processes Our problem of course is the data. This is what we are trying to address. RE: collaborative grading: good pd opportunity but now trying to get more accurate data
- #4 Use articles here. Very quick.
- #5 We need to be having students self-reflect all the time. Susan Muir’s idea: Laminate and cut in strips. Have students self reflect and peer assess. Save work from the past for “anchor papers” . We saved some this year. Anchor vs exemplar
- #6 The rubric is not cut and dried. What is an error? What is correct and accurate representation? Ex: the commas in large numbers as printed in the problem: Big deal or not? Zeros before decimals? What is “audience”? The areas of the rubric overlap! A representation is a form of communication! We all see things differently, and this leads to discrepancies in how we mark. Pose question: Someone draws a graph, correct, forgets to label axes. How do you consider this error? Pair talk One person my give good scores for representation, but call lack of labels on a graph a “communication” issue, others will see it as a representation issue. Is the lack of labels considered under both headings? Someone has a list of multiplication facts: 5X3=15, 5X4=20, 5X5=10, 5X6=30. This list of multiplication is an extension of the addition pattern in the problem, the problem has the correct answer. Can this student be an expert? A lot of our beliefs and values are reflected in how we interpret the rubric! This is a subjective process, it is wholistic. Like teaching, it is emotional and personal. How can we get our assessment results to be meaningful? We need to step back and look from a distance: A lot of “Novice” says something. A lot of “expert” says something. The borderline between Apprentice and Practionioner is fuzzy. The lines between processes are fuzzy: I can’t see your connections unless you communicate them to me. We are looking at trends. What data is important to us? In what ways is it important?
- #8 Kelsey Shields and Candice Gale
- #9 Give Handout on “connections”
- #10 The ONLY way we can learn something is to tie it to something we already know. We always teach math by using connections!! Its in every lesson! Try to think of a time you don’t connect! What we are asking students to do is recognize those connections that they are making. Math to real life is a lower level connection, though still valid and important. Sometimes though they are quite contrived. Can we blame kids for contriving in math???We do it to them all the time! We are looking for math to math connections as rich connections.
- #12 Without communicating, kids can neither make nor demonstrate mathematical connections. Again, the rubric is fuzzy!
- #13 Handout from Ontario Math. Good ideas. Gallery walk Communicating is both oral and written. We need to coach kids to have quality dialogue. When we are in math class we think and speak like mathematicians. We will construct logical arguments. We will explain clearly and provide proof. We will use appropriate dialogue! By practicing “talking the talk” maybe we can improve the written portion of the dialogue. Writing in math is very personal, forces students to construct and clarify meaning, provide argument and proof, and recognize symbols, diagrams, equations and other representation as an efficient form of communication. I know its hard to find time, but we need to discuss. Not just with benchmarking problems, but using other rich problems (problem solver), open ended tasks (make your own!!) and even textbook practice. How do we engage reluctant speakers? Redirect, provide warning, plan for dialogue.
- #15 Talking probes!
- #17 RTI outline says no diagrams, does not apply to math. Diagrams and visuals are good. Interact with word wall Effect size of vocabulary programs .67 (significant). Real learning in math does not happen through rote memorization (though that is still a part of what we need to do!!). Real learning happens through discussion and debate, consolidating ideas.
- #19 Types of discrepancies in conversations: What answers are acceptable? What vocabulary are we looking for? How much? Everyday language is math language for K-3. Example of graders trapped in criteria b/c they specified words What representations are appropriate? Inappropriate? Tally marks? Bar graphs? What strategies are acceptable? If an algebraic strategy is used rather than an arithmetic one, do we consider that a stronger solution? In gr 8 2013 we started out saying no to this, but later in the marking it became evident that people were considering an algebraic equation to be a more sophisticated solution. Connections can be anywhere throughout the problem. What if they do it right, then add something, another diagram or whatever, that is wrong? We can’t pretend we didn’t see something if it is a genuine misconception. What is a mistake? A computation or conceptual error vs a “slip of the pencil” error. Yes its subjective but is objective more accurate in terms of grading student ability Is more better??
- #20 Reeves talks about the “perils of specificity” when it comes to rubrics. He states clearly that rubrics are subjective, and that we need to have appropriate modesty about our grading practices. The point here is: Our own grading practices are pretty subjective too, no matter what. There is vast inconsistency in grades among teacher!
- #22 What is a valid extension? I could write a rule that I could use to figure out how much it would cost to shingle any number of houses. We have had people give almost no credit for good connections because the template prompted students to make a connection, and the student wrote “I can’t”. Yet there are great connections throughout the paper
- #24 The one with visualizing first is a very non threatening way to enter in to a problem. Prompting for connections: In the past, markers have assumed that is the only place to look for connections. Things that have worked well: Use a word wall, refer to it, have students circle or list appropriate math language (honestly they are teaching the teachers here! Helping out the assessors!) Have a check list: Go back through your work. What connections can you make: Math to self, to world, other subjects, math to math? Checklist: Go back through your problem. What mathematical connections have you made? What representations have you chosen? Is it accurate? Check your work! Can’t get to practitioner with the wrong answer! Teach problem solving all the time Have discussions Work on one part at a time.. Just visualize! Just connect. Just represent, etc. Give the answer if you need to in order to get students past the anxiety
- #25 Where do you see connections? Math to self and math to life connections are valid for K-3. In this problem, one student argued that you couldn’t put cows in pens with sheep, that wasn’t’ good for them. Another student drew feeders in all the pens and labelled the hay and water. Someone drew different fencing for the sheep. Connections?
- #26 Establish criteria together, like we do Use anchors Have students make friendly suggestions to one another (peer assess). Practice “sandwich” feedback. Have students model to each other. Model with a teacher. Analyze one process at a time. Have students continually think in terms of assessment Video???