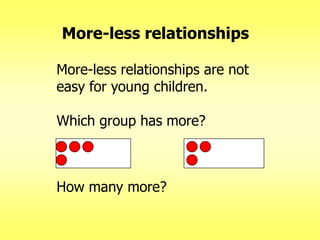
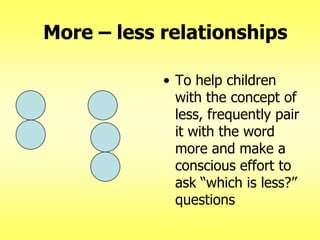
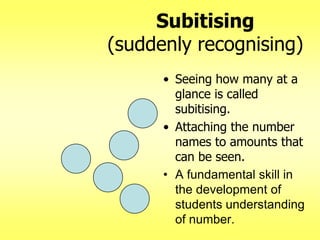
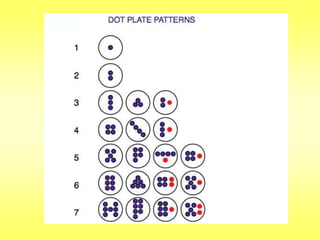
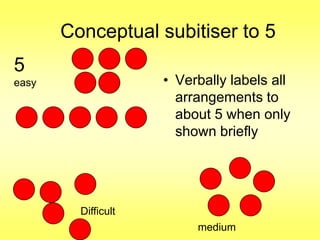
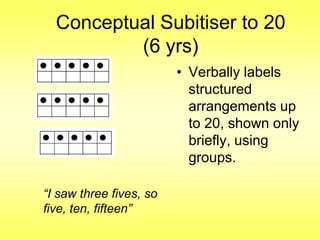
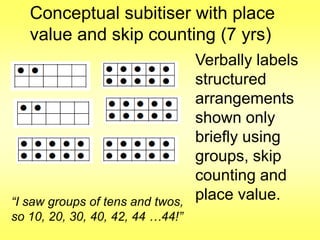
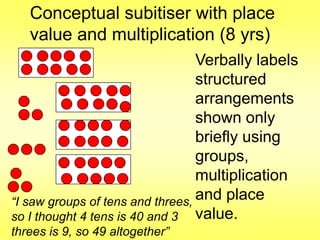
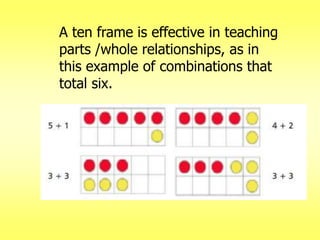
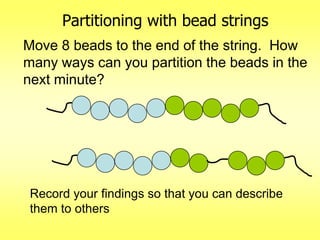
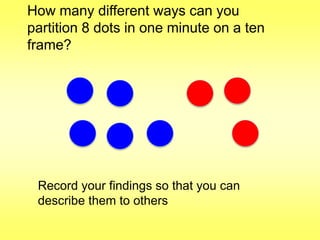
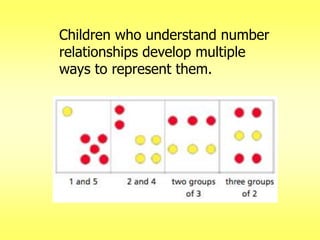
The document addresses common misconceptions about mathematics education for young children, asserting that all children are capable of engaging with mathematics, which should not be viewed as an isolated subject. It emphasizes the importance of intentional teaching practices that foster inquiry, model problem-solving, and support children's mathematical development through interactive learning experiences. Furthermore, it highlights key mathematical concepts, such as understanding more-less relationships and counting principles, essential for early number sense.

1. Debunking misconceptions
about mathematics in the
early years

2. Overview
1. Common misconceptions
2. Critical mathematical ideas underpinning
number sense
3. The role of the early childhood educator

3. Common misconceptions
Young children are not ready for mathematics
education.
Mathematics is for some bright kids with
mathematics genes.
Simple numbers and shapes are enough.
Language and literacy are more important than
mathematics.
Teachers should provide an enriched physical
environment, step back, and let the children play.

4. Common misconceptions
Mathematics should not be taught as stand-alone
subject matter.
Assessment in mathematics is irrelevant when it
comes to young children.
Children learn mathematics only by interacting
with concrete objects.
Computers are inappropriate for the teaching and
learning of mathematics.
Retrieved from
http://www.earlychildhoodaustralia.org.au/australian_journal_of_early_childhood/ajec_index_abstracts/early_childhood
_teachers_misconceptions_about_mathematics_education_for_young_children_in_the_united_states.html

5. Intentional teaching and the Early Years
Learning Framework
About ‗intentional teaching‘
•Intentional teaching is one of the 8 key pedagogical
practices described in the Early Years Learning
Framework (EYLF).
•The EYLF defines intentional teaching as ‗educators
being deliberate purposeful and thoughtful in their decisions
and actions‘.
Intentional teaching is thoughtful, informed and
deliberate.

6. Intentional teaching and the Early
Years Learning Framework
Intentional educators:
•create a learning environment that is rich in materials
and interactions
•create opportunities for inquiry
•model thinking and problem solving, and challenge
children's existing ideas about how things work.

7. Intentional teaching and the Early Years
Learning Framework
Intentional educators:
•know the content—concepts, vocabulary, skills and
processes—and the teaching strategies that support
important early learning in mathematics
•carefully observe children so that they can thoughtfully
plan for children‘s next-stage learning and emerging
abilities
•take advantage of spontaneous, unexpected teaching and
learning opportunities.

8. Numeracy or Mathematics?
―Numeracy is the
capacity, confiden
ce and disposition
to use
mathematics I
daily life‖
EYLF, 2009 p.38

9. Five proficiencies
1. Conceptual understanding
2. Procedural fluency
3. Strategic competence- idea of choosing
what is going to be an appropriate
method to solve problems.
4. Adaptive reasoning - reason to other
contexts
5. Productive disposition- most important

10. Disposition of children
Encourage young children to see
themselves as mathematicians by
stimulating their interest and ability in
problem solving and investigation
through
relevant, challenging, sustained and
supported activities (AAMT and ECA
2006)

11. Low mathematical skills in the earliest years
are associated with a slower growth rate –
children without adequate experiences in
mathematics start behind and lose ground
every year thereafter.
(Clements and Sarama, 2009, p. 263)
Interventions must start in pre K and
Kindergarten (Gersten et al 2005). Without
such interventions, children in special need
are often relegated to a path of failure
(Baroody, 1999)

12. Critical concepts
underpinning number sense

13. More – less
Counting
Subitising
Part part whole

14. More-less relationships
More-less relationships are not
easy for young children.
Which group has more?
How many more?

15. More-less relationships
Four-year-olds may
be able to judge
which of two
collections has more,
but determining how
many more (or less)
is challenging, even
when they count.

16. More-less relationships
• Young children must arrive at the
important insight that a quantity (the
less) must be contained inside the
other (the more) instead of viewing
both quantities as mutually exclusive.
The concept requires them to think of
the difference between the two
quantities as a third quantity, which is
the notion of parts-whole.

17. More – less relationships
• To help children
with the concept of
less, frequently pair
it with the word
more and make a
conscious effort to
ask ―which is less?‖
questions

18. Make sets of more/less/same
For all three concepts, more, less and
the same children should construct
sets involving counters as well as
make comparisons or choices between
two sets.

19. Diffy Towers
• Organise students into pairs and provide each
pair with a die and a supply of Unifix blocks. The
first student rolls a die, takes a corresponding
numberof Unifix blocks from a central pile and
builds a tower with them. The second student rolls
the die and repeats the process. They then
compare the two towers to see who has the most
blocks and determine the differencebetween the
two towers. The player with the larger number of
blocks keeps the difference and all other blocks
are returned to the central pile.
• The activity continues until one student
accumulates a total of ten blocks

20. Stages in comparison
1. There are more blue than red and there are less
red than blue
2. There are seven more blue than red and seven
less red
3. Ten is seven more than three and three is seven
less than ten

21. One and two
more, one and two
less
The two more and two less
relationship involve more than just the
ability to count on two or count back
two. Children should know for
example that 7 is 1 more than 6 and
also 2 less than 9.

22. When Harry was at the circus, he saw 8 clowns
come out in a little car. Then 2 more clowns came
out on bicycles. How many clowns did Harry see
altogether?
Ask different students to explain how they got
their answer of ten. Some will count on from 8.
Some may need to count 8 and 2 and then
count all. Others will say they knew that 2 more
than 8 is 10.
The last response gives you an opportunity to
talk about the 2 more than idea.

23. Early counting
The meaning attached to
counting is the key conceptual
idea on which all other number
concepts are developed

24. Principles of Counting
• Each object to be counted must be touched or „included‟
exactly once as the numbers are said.
• The numbers must be said once and always in the
conventional order.
• The objects can be touched in any order and the starting
point and order in which the objects are counted doesn‟t
affect how many there are.
• The arrangement of the objects doesn‟t affect how many
there are.
• The last number said tells „how many‟ in the whole
collection, it does not describe the last object touched.

25. Principles of Counting
• Which of the principles of counting
does Charlotte understand?

26. Principles of Counting
• Each object to be counted must be touched or „included‟
exactly once as the numbers are said.
• The numbers must be said once and always in the
conventional order.
• The objects can be touched in any order and the starting
point and order in which the objects are counted doesn‟t
affect how many there are.
• The arrangement of the objects doesn‟t affect how many
there are.
• The last number said tells „how many‟ in the whole
collection, it does not describe the last object touched.

27. To develop their understanding
of counting, engage children in
any game or activity that
involves counts or comparisons.

28. Trusting Counting
There are many children who know the
number string well enough to respond
correctly to „how many‟ questions without
really understanding that this is telling
them the quantity of the set.
1, 2, 3, 4, 5, 6, 7,…
2, 4, 6, 8, 10, …

29. Intentional opportunities for
counting
• Model counting experiences in meaningful
contexts, for example, counting girls, boys as
they arrive at school, counting out pencils at the
art table.
• Involving all children in acting out finger plays
and rhymes and reading literature, which models
the conventional counting order.
• Seize upon teachable moments as they arise
incidentally. “Do we have enough pairs of
scissors for everyone at this table?”

31. Pick up chips :
• Take a card from the
pile and pick up a
corresponding number
of counters.
• Play until all the cards
have been taken.
• The winner is the
person with the most
chips at the end of the
game.

32. Sandwich boards
Ask students why
they lined up the
way they did.
• Add string to numeral cards
so they can be hung around
the students necks. Provide
each student with a numeral
card. Students move
around the room to music.
Once the music stops, the
children arrange themselves
into a line in a correct
forward or backward
number sequence.

33. Using number lines

34. Ordinal number
“I was first to school today”

35. Counting on and back
• The ability to count on is a
“landmark” in the development of
number sense.
Fosnot and Dolk (2001)

36. “Real Counting on”
First player turns over the top
number card and places the
indicated number of counters
in the cup. The card is placed
next to the cup as a reminder
of how many are there. The
second player rolls the die
and places that many
counters next to the cup.
Together they decide how
many counters in all.

37. Calculator counting
Calculator counting contributes to
a better grasp of large
numbers, thereby helping to
develop students number sense.
―It is a machine
to engage children
in thinking about
mathematics‖
(Swan and Sparrow 2005)

38. The calculator provides an
excellent counting exercise for
young children because they see
the numerals as they count

39. Anchors or
‘benchmarks’ of 5 and
10
Since 10 plays such a large role in our
numeration system and because two
fives make ten, it is very useful to
develop the relationships for the
numbers 1 to 10 to the important
factors of 5 and 10.

40. Race to five/ten on a ten
frame
•Roll the 3 sided or 6 sided
die and count the dots.
•Collect the corresponding
number of counters and
place them on the five/ten
frame.
•The exact number needed
to complete the ten frame
must be rolled to finish.

41. These early number ideas are basic
aspects of number. Unfortunately, too
may traditional programs move
directly from these beginning ideas to
addition and subtraction, leaving
students with a very limited collection
of ideas about number to bring to
these topics. The result is often that
children continue to count by ones to
solve simple story problems and have
difficulty mastering basic facts.

42. Subitising
(suddenly recognising)
• Seeing how many at a
glance is called
subitising.
• Attaching the number
names to amounts that
can be seen.
• A fundamental skill in
the development of
students understanding
of number.

43. Subitising
(suddenly recognising)
• Promotes the part part
whole relationship.
• Plays a critical role in the
acquisition of the concept
of cardinality.
• Children need both
subitising and counting to
see that both methods give
the same result.

45. Conceptual subitiser to 5
5
• Verbally labels all
arrangements to
about 5 when only
shown briefly
easy
Difficult
medium

46. Conceptual Subitiser to 20
(6 yrs)
• Verbally labels
structured
arrangements up
to 20, shown only
briefly, using
groups.
“I saw three fives, so
five, ten, fifteen”

47. Conceptual subitiser with place
value and skip counting (7 yrs)
“I saw groups of tens and twos,
so 10, 20, 30, 40, 42, 44 …44!”
Verbally labels
structured
arrangements
shown only
briefly using
groups, skip
counting and
place value.

48. Conceptual subitiser with place
value and multiplication (8 yrs)
Verbally labels
structured
arrangements
shown only
briefly using
groups,
multiplication
“I saw groups of tens and threes, and place
so I thought 4 tens is 40 and 3 value.
threes is 9, so 49 altogether”

49. Part whole
relationships
To conceptualise a number as being
made up of two or more parts is the
most important relationship that can
be developed about numbers.

50. A ten frame is effective in teaching
parts /whole relationships, as in
this example of combinations that
total six.

51. Missing Cubes

52. Partitioning with bead strings
Move 8 beads to the end of the string. How
many ways can you partition the beads in the
next minute?
Record your findings so that you can describe
them to others

53. How many different ways can you
partition 8 dots in one minute on a ten
frame?
Record your findings so that you can
describe them to others

54. How many different ways are there
for 5 frogs to be, in and out of the
water?
What if there were 7
frogs? Can you find a
pattern?

55. Children who understand number
relationships develop multiple
ways to represent them.

56. • Understanding part-part-whole
relationships will enhance
children‘s flexibility, enabling them
to represent problems in different
ways, so they can choose the most
helpful.

57. Relationships for
numbers 10 to 20
A set of ten should play a major role in
children‟s initial understanding of number
between 10 and 20. When children see a
a set of six and a set of ten, they should
know without counting that the total is 16

58. 3. The role of the Early
childhood educator

59. Role of the educator
Model mathematical language.
Ask probing questions.
Build on children‘s interests and natural
curiosity.
Provide meaningful experiences.
Scaffold opportunities for learning &
model strategies.
Monitor children‘s progress and plan for
learning.

60. Probing Questions
A crucial part of a teacher‟s role is to develop students‟
ability to think about mathematics. To develop thinking
processes teachers need to ask higher-order questions
that require students to interpret, apply, analyse and
evaluate information.
Encourage students to ask questions of each other so
that they begin to develop maturity of thought.

61. The pedagogy
• … less teacher talk, with the learning coming as
a result of the experience with the task and
children sharing their insights.
• A culture of “not telling”
Listening to children
Encourage persistence
Probing questions
• Learning involves struggle. They are not
learning if it‟s not a struggle
Long „wait‟ time
Time to reflect on their actions

62. “We use the word struggle to mean that
students expend effort to make sense of
mathematics, to figure something out that is
not immediately apparent. We do not use
struggle to mean needless frustration... The
struggle we have in mind comes from solving
problems that are within reach and grappling
with key mathematical ideas that are
comprehendible but not yet well formed”
Hiebert and Grouws, 2007

63. Assessment methods
Collect data by observation and or/listening to
children, taking notes as appropriate
Use a variety of assessment methods
Modify planning as a result of assessment

64. References
AAMT & ECA. (2006). Position paper on Early Childhood Mathematics.
www.aamt.edu.au
www.earlychildhoodaustralia.org.au
DEEWR. (2009). Belonging, Being & Becoming: The Early Years Learning Framework
for Australia.
http://www.deewr.gov.au/earlychildhood/policy_agenda/quality/pages/earlyyearslearningf
ramework.aspx
Hiebert, J., &Grouws, D. A. (2007). The effects of classroom mathematics teaching on
students‟ learning. Second handbook of research on mathematics teaching and learning,
1, 371-404.
Sarama, J., & Clements, D. H. (2009). Early childhood mathematics education research:
Learning trajectories for young children. Routledge.