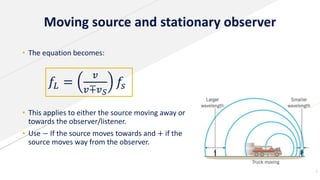
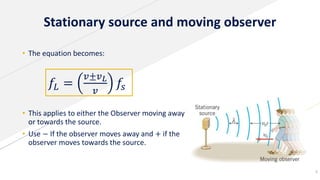
The Doppler effect refers to the change in frequency of a wave as the source and observer move relative to each other. The document discusses the history of the Doppler effect and its discovery by Doppler in 1842. It defines key terms like frequency and wavelength and presents the Doppler effect equation. Examples are given of how the equation applies to moving sources and observers. Real-life applications like monitoring blood flow and fetal heartbeats using Doppler are also mentioned.

1. Doppler Effect
Presented by MABEGWANE BL

2. FR
2
History of Doppler Effect
• The Doppler effect is named after Austrian physicist
J. C. Doppler, who first described it for sound in
1842 when he studied the behaviour of waves as the
source, receiver or both are moving.
• He proposed that as the source is moving the waves
at the front have a higher frequency compared to
the source being stationary.
• The variation in frequencies is noticed by human
ears as the change in pitch as the source moves.

3. FR
3
What is Doppler Effect?
Doppler effect is the apparent change in
frequency and wavelength of a wave when
the observer and the source of the wave
move relative to each other.
• If the objects are coming closer to one
another, the frequency increases
• If they are moving farther away from
each other, the frequency decreases
• An example is the changing sound of a
taxi hooter or ambulance as it drives
past.

4. • Wavelength (𝝀) – distance between corresponding
points of two consecutive waves.
• Frequency (𝒇) – the number of waves that passes a
given point per second, measured in Hertz.
• Velocity (𝒗) – the rate of change in position of an
object.
• The relationship between the above concepts is given
by:
Doppler effect concepts
𝑣 = 𝑓𝜆
My favorite frequency is
50 000 Hz
You’ve probably never
Heard it before

5. FR
Doppler effect equation
5
Where:
• 𝒇 𝑳 – frequency of the listener or observer
• 𝒇 𝒔 – frequency of the source of sound
• 𝒗 – speed of sound in air, and equals 343m/s
• 𝒗 𝑳 – velocity of the listener/observer
• 𝒗 𝑺 – Velocity of the source.
Condition for doppler effect to occur is the that there must be relative motion between
the source and the listener.
𝑓𝐿 =
𝑣±𝑣 𝐿
𝑣∓𝑣 𝑆
𝑓𝑠

6. FR
Doppler effect Scenarios
6
Three scenarios for doppler effect are:
• Moving source and stationary observer
• Stationary source and moving observer
• Moving source and observer
Daily life scenario
• You’re standing on the side of a road and suddenly you hear a distant siren from
behind you. As an ambulance approaches you, the sound of its siren gets louder
and louder. But once the ambulance passes you, the sound of its siren gets softer.
Why?
• Well, it’s because of the Doppler effect!

7. Moving source and stationary observer
7
• The equation becomes:
• This applies to either the source moving away or
towards the observer/listener.
• Use − If the source moves towards and + if the
source moves way from the observer.
𝑓𝐿 =
𝑣
𝑣∓𝑣 𝑆
𝑓𝑠

8. Stationary source and moving observer
8
• The equation becomes:
• This applies to either the Observer moving away
or towards the source.
• Use − If the observer moves away and + if the
observer moves towards the source.
𝑓𝐿 =
𝑣±𝑣 𝐿
𝑣
𝑓𝑠

9. FR
Moving source and observer
9
The equation is the original general doppler
effect equation:
• Numerator:
+ is used when the observer moves
towards the source
− is used when the observer moves
away from the source
• Denominator:
− is used when the source moves
towards the observer
+ is used when the source moves away
from the observer
𝑓𝐿 =
𝑣±𝑣 𝐿
𝑣∓𝑣 𝑆
𝑓𝑠
𝑣 𝐿𝑣 𝑆

10. FR
Example
10
Metro rail is an operator of commuter
rail services in major urban areas of
south Africa. At a train station in
Johannesburg, commuters stand on
the railway platform waiting for a train.
As the train approaches the platform at
a speed of 25 m/s, it blows the horn at
a frequency of 775 Hz, to alert the
commuters. What is the frequency
observed by the commuters standing
on the platform?

11. FR
Solution
11
• In this case we have, a moving source(train) and a stationary
observer(commuters), therefore we use: 𝑓𝐿 =
𝑣
𝑣∓𝑣 𝑆
𝑓𝑠
• The source of sound is moving towards the observer, thus we use − sign.
=
343
343 − 25
775
= 835,9 𝐻𝑧
𝑓𝐿 =
𝑣
𝑣 − 𝑣 𝑆
𝑓𝑠

12. Applications of Doppler effect
12
Doppler
Effect
Detection and
characterization
of blood flow
Detection of foetal
heart
Blood pressure
monitoring

13. FR
13
References
• Booth, D. (2015) Doppler effect. Available from Slideshare at
https://www.slideshare.net/sanganak624/doppler-effect-54587282?qid=50ee9120-
0ae3-458d-a736-084799c1643d&v=&b=&from_search=4 (Accessed 18 August 2020)
• Katieliw. (2015) The Doppler Effect. Available from Slideshare at
https://www.slideshare.net/katieliw/the-doppler-effect-45304450?qid=542929ff-05aa-
4c2c-ba43-2210ca6673a2&v=&b=&from_search=16 (Accessed 18 August 2020)
• Sihota, T. (2015) Lo5 - The Doppler Effect and Bats. Available from Slideshare at
https://www.slideshare.net/tiannasihota/lo5-45298737 (Accessed 18 August 2020)
• Nguyen, V. (2015) The Doppler Effect. Available from Slideshare at
https://www.slideshare.net/vn24/the-doppler-effect-45304199 (Accessed 18 August
2020)

14. FR
14
• Mychiejw. (2015) Doppler Effect. Available from Slideshare at
https://www.slideshare.net/mychiejw/doppler-effect-45304367?qid=542929ff-05aa-
4c2c-ba43-2210ca6673a2&v=&b=&from_search=18 (Accessed 18 August 2020)
• Small, R. (2016) Doppler effect. Available from Slideshare at
https://www.slideshare.net/RamseySmall/doppler-effect-69641341 (Accessed 18
August 2020)