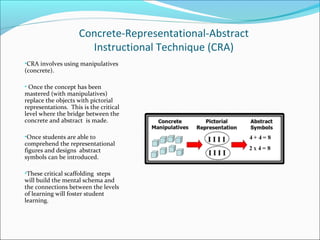
The document discusses issues students with disabilities face in math including perceptual, language, reasoning, and memory challenges. It then describes considerations for instruction including differentiated instruction, metacognitive strategies, progress monitoring, and the use of instructional technology and Universal Design for Learning to address diverse needs. Specific strategies are provided such as concrete-representational-abstract instruction, mnemonic devices, graphic organizers, and technology tools to enhance math curriculum.

1. Issues and solutions
Jane Iannacconi

2. Math
Various research–
based instructional
methods and
strategies will be
described, to address
the revised standards
in math for teachers
to effectively meet
the learning needs of
students with
disabilities.

3. Current Issues to Consider
Changing Policies- No Child Left Behind Act
Changing Standards in Mathematics- new federal
requirements and mandates related to accountability.
Characteristics of Students with Disabilities.
Perceptual skills
Language
Reasoning
Memory

4. Perceptual Skills
Difficulty with spatial relationships, distances, and
sequencing.
May interfere with the acquisition of and
demonstration of math concepts and skills (e.g.,
estimating size, distance, and problem solving.).

5. Language
Vocabulary and language of mathematical concepts is
not only varied but abstract.
Students with disabilities in the area of language may
also have difficulties understanding certain
mathematical concepts.
First, second, greater than, less than, vertex,
complementary, and acute are a few such terms.

6. Reasoning
Students with disabilities may not posses the abstract
reasoning skills necessary for higher level math skills
development.
This may present problems if instruction in
mathematics is at the conceptual, abstract level.

7. Memory
Many students with learning and behavioral
disabilities have difficulties remembering information
that was presented.
Especially evident with abstract symbols associated
with mathematics (e.g., minus, greater than, less than,
etc.).

8. Considerations for Instruction in
Mathematics
1. Differentiated instruction.
2. Metacognitive strategies and instructional routines.
3. Progress monitoring and formative assessment
procedures.
4. Computer-assisted instruction and Universal Design
for Learning (UDL).

9. Instructional Technology and Universal Design for
Learning (UDL)
Calls for design of structures that anticipate the needs
of individuals with disabilities and accommodate
these needs from the outset.

10. Differentiated Instruction
This approach to planning and
teaching is based on the
premise that one must
consider who they are
teaching as well as what they
are teaching.
This type of instruction must
include clarity of the
standards and learning goals
of the curriculum, on-going
assessment and adjustment,
use of flexible grouping, and
planning learning activities
that are respectful of each
students needs.

11. Concrete-Representational-Abstract
Instructional Technique (CRA)
•CRA involves using manipulatives
(concrete).
• Once the concept has been
mastered (with manipulatives)
replace the objects with pictorial
representations. This is the critical
level where the bridge between the
concrete and abstract is made.
•Once students are able to
comprehend the representational
figures and designs abstract
symbols can be introduced.
•These critical scaffolding steps
will build the mental schema and
the connections between the levels
of learning will foster student
learning.

12. Metacognitive Strategies and Instructional
Routines
Refers to higher order thinking that involves active control over the
cognitive process.
These strategies teach students; how to think about what they are
doing.
They include using mnemonic devices, prior knowledge prompts,
problem solving routines, and graphic organizers.

13. Mnemonic Devices- Strategies that students and teachers can create to
help students remember content. The verbal information promotes recall of
unfamiliar information and content.
FIRST is a mnemonic device for creating mnemonics.
F - Form a word (Example: FIRST)
I - Insert extra letters to form a mnemonic. (If needed)
R - Rearrange the first letters to form a mnemonic word.
S - Shape a sentence to form a mnemonic.
T -Try combinations of the first four steps to create a mnemonic
Please Excuse My Dear Aunt Sally or PEMDAS to remember the order of
operations Parenthesis, Exponent, Multiplication & Division (left to right),
Addition & Subtraction (left to right)

14. Prior Knowledge
Prompts
Prior Knowledge Prompt
Relates new learning to
existing knowledge. K-W-L
promotes learning by helping
students retrieve relevant
information and learn with
awareness.
___________________________
(K) (W) (L)
___________________________
 How to use: Before introduction of a topic, students
write down and discuss, what they know (k) (or
think they know).
 What they want (w) to learn about the topic. During
the study, the teacher responds to and/or corrects
any of the information originally discussed about the
topic.
 Students record what they learned (L).

15. Problem Solving Strategies
Problem Solving Strategies
provide steps to follow in
solving problems. It is very
common to use a mnemonic to
outline the steps to solve a
problem.
FAST is a mnemonic device for basic
problem solving.
F ind what you’re solving for.
A sk yourself, “What are the parts of the
problem?”
S et up the numbers.
T ake down the sign.
CAP is mnemonic device for solving basic
one-variable algebra equations
C ombine like terms.
A sk yourself, “How can I isolate the
variable?”
P ut the value of the variable in the initial
equation and check if the equation is
balance.

16. Graphic Organizers
Visual, pictorial displays of
information purposefully
arranged in a meaningful way.
The common attribute
underlying the various graphic
organizers is the visual-spatial
arrangement of information
linking words or statements
that are connected in a
meaningful way.

17. Progress Monitoring and Formative
Assessment
 Assessment tasks should match student’s needs, the curriculum, and
instructional strategies.
 Assessments should be viewed as a tool to assist the teacher design and revise
instruction for the student.
 Assessment should also include observations, interviews, checklists, and
rating scales.
 Student performance increases when teachers make instructional adjustments
based on individual curriculum-based measurement data.

19. Instructional Technology and Universal Design for
Learning (UDL)
This calls for the design of structures that anticipate the needs of
students with disabilities and accommodates these needs from the
outset.
Traditional curricula may present barriers that limit students’ access
to information and learning. UDL curriculum is designed to be
flexible, enriched with multiple media, including assistive technology,
to take on the burden of adaptation so the learners do not have to.

20. Effective Curriculum Enhancements
 Anchor Instruction
 Modify Text
 Text-to-Speech
 Manipulatives
 Simulations/Virtual Reality
 Technology Tools

21. Anchor Instruction
Creating authentic contexts within which to teach targeted
mathematics concepts/skills/strategies requires teachers to think of
ways the mathematics concept/skill/strategy occurs in naturally
occurring contexts that hold meaning for the students they teach.
When doing this, it is helpful to consider your students' age-related
interests, cultural/community interests, and common experiences
your students share.
Use authentic problem solving situations in conventional and digital
environments.
Have students compare heights, distance, or temperature using
some of the latest calculators.

22. Text
Modify Text Text-to-Speech
Change text to match the
interest of students
Change text to match the
reading level of students
Audio textbooks
Have students record their
work through digital pictures
and verbal exercises.

23. Manipulatives
•Use of concrete objects
is important for
conceptual learning
•Use concrete objects
that match the purpose
of the lesson
•Concrete objects
should be at a level that
the students will
understand.

24. Simulations/Virtual Reality
Interacting with media
that shows the concept
to the student.
Allows the student to
see the social relevance
of a standard and how
they might use the
information.

25. Technology Tools
Calculators
Internet
Concrete objects
All work to increase student interactions with the
mathematical skills and concepts

26. Technology Tools
Student Characteristic Resources
 Antonio’s mind tends to wander in
math class, but he can stay on task
if he has a visual representation of
the lesson’s concepts.
___________________________
 Steven is a bright student in
understanding math concepts,
however, has difficulty decoding
and understanding the vocabulary
contained in math
problems.
Cool Math
http://coolmath.com/
___________________________
All Math
http://www.allmath.com/glo
ssary.php?page=a

27. Technology Tools
Student Characteristic Recourses
 Marcus understands complex
math concepts at the concrete level, using
manipulatives. However, his gross and fine
motor skills, as well as his in class behaviors,
limit his use of manipulatives.
__________________________________________
_
 Susan learns her math facts, but needs to
develop increased accuracy and fluency with
this skill.
__________________________________________
_
 Gizmos
www.explorelearning.com
___________________________
 Math Resources:
http://www.carrollk12.org/ees/mathreso
urces/default.asp
_____________________________________

28. References
Little, M. E. (2009). Teaching mathematics: issues and
solutions. TEACHING exceptional children plus.6(1),
pages 1-15. Retrieved [September 3, 2010] from
http://journals.cec.sped.org/index.cfm