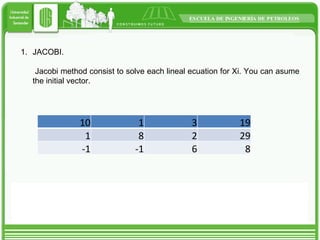
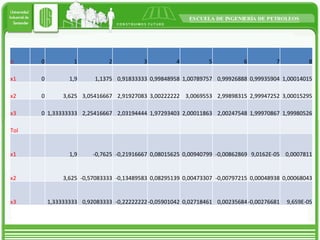
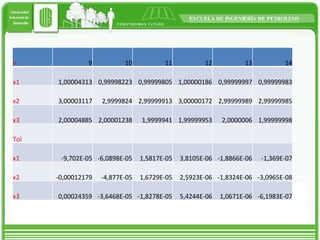
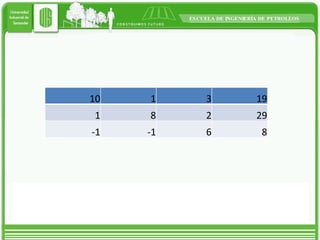
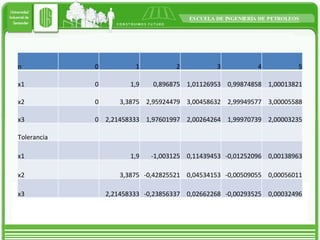
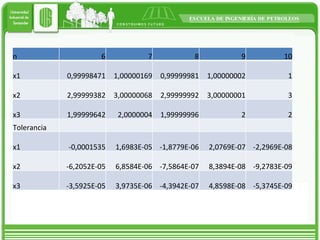
This document discusses two iterative methods for solving systems of linear equations: Jacobi and Gauss-Seidel. Jacobi method works by solving each equation for the unknown variable, using initial guesses. Gauss-Seidel is similar but uses the most recently calculated value in each step to improve on Jacobi. An example applying each method to a 3x3 system is shown, with Gauss-Seidel converging faster in fewer iterations.

1. RUBEN DARIO ARISMENDI RUEDA

2. CHAPTER 4: ‘Iterative Methods to solve lineal ecuation systems’

3. INTRODUCTION In the next presentetion, there will be some examples that are already solved in excel document but the interesting part is to see how each different method behaves. To use Jacobi method, the matrix has to has a prevailing diagonal. ( the addition of the other terms are less than the term of the diagonal)

4. JACOBI. Jacobi method consist to solve each lineal ecuation for Xi. You can asume the initial vector. 10 1 3 19 1 8 2 29 -1 -1 6 8

5. n 0 1 2 3 4 5 6 7 8 x1 0 1,9 1,1375 0,91833333 0,99848958 1,00789757 0,99926888 0,99935904 1,00014015 x2 0 3,625 3,05416667 2,91927083 3,00222222 3,0069553 2,99898315 2,99947252 3,00015295 x3 0 1,33333333 2,25416667 2,03194444 1,97293403 2,00011863 2,00247548 1,99970867 1,99980526 Tol x1 1,9 -0,7625 -0,21916667 0,08015625 0,00940799 -0,00862869 9,0162E-05 0,0007811 x2 3,625 -0,57083333 -0,13489583 0,08295139 0,00473307 -0,00797215 0,00048938 0,00068043 x3 1,33333333 0,92083333 -0,22222222 -0,05901042 0,02718461 0,00235684 -0,00276681 9,659E-05

6. n 9 10 11 12 13 14 x1 1,00004313 0,99998223 0,99999805 1,00000186 0,99999997 0,99999983 x2 3,00003117 2,9999824 2,99999913 3,00000172 2,99999989 2,99999985 x3 2,00004885 2,00001238 1,9999941 1,99999953 2,0000006 1,99999998 Tol x1 -9,702E-05 -6,0898E-05 1,5817E-05 3,8105E-06 -1,8866E-06 -1,369E-07 x2 -0,00012179 -4,877E-05 1,6729E-05 2,5923E-06 -1,8324E-06 -3,0965E-08 x3 0,00024359 -3,6468E-05 -1,8278E-05 5,4244E-06 1,0671E-06 -6,1983E-07

7. n 15 16 17 x1 1,00000002 1,00000001 1 x2 3,00000003 3,00000001 3 x3 1,99999995 2,00000001 2 Tol x1 1,8904E-07 -8,8137E-09 -1,6392E-08 x2 1,7207E-07 -1,6636E-08 -1,3945E-08 x3 -2,7978E-08 6,0186E-08 -4,2416E-09

8. 2. GAUSS-SEIDEL. The algoritm is the same for the Jacobi method. But it makes an exception with the next expression that improve the Jacobi’s method.

9. 10 1 3 19 1 8 2 29 -1 -1 6 8

10. n 0 1 2 3 4 5 x1 0 1,9 0,896875 1,01126953 0,99874858 1,00013821 x2 0 3,3875 2,95924479 3,00458632 2,99949577 3,00005588 x3 0 2,21458333 1,97601997 2,00264264 1,99970739 2,00003235 Tolerancia x1 1,9 -1,003125 0,11439453 -0,01252096 0,00138963 x2 3,3875 -0,42825521 0,04534153 -0,00509055 0,00056011 x3 2,21458333 -0,23856337 0,02662268 -0,00293525 0,00032496

11. n 6 7 8 9 10 x1 0,99998471 1,00000169 0,99999981 1,00000002 1 x2 2,99999382 3,00000068 2,99999992 3,00000001 3 x3 1,99999642 2,0000004 1,99999996 2 2 Tolerancia x1 -0,0001535 1,6983E-05 -1,8779E-06 2,0769E-07 -2,2969E-08 x2 -6,2052E-05 6,8584E-06 -7,5864E-07 8,3894E-08 -9,2783E-09 x3 -3,5925E-05 3,9735E-06 -4,3942E-07 4,8598E-08 -5,3745E-09

12. With the two last examples, we can see that the Gauss-Seidel method is more efficient than the Jacobi method. Because it gets to the answer in a less number of iterations.