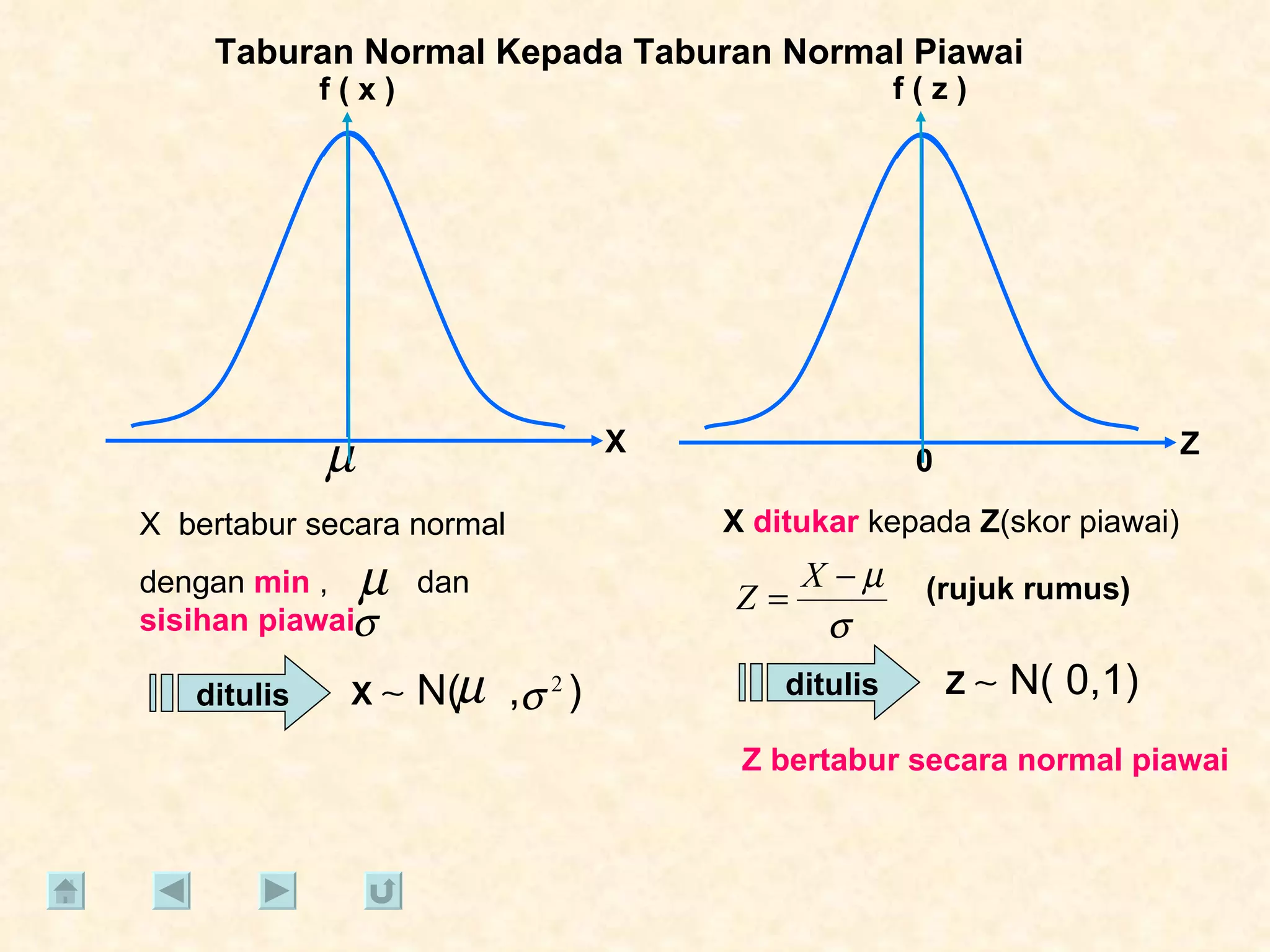
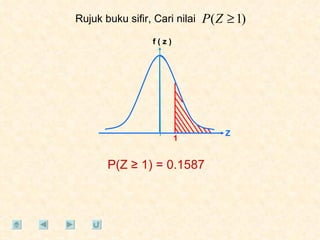
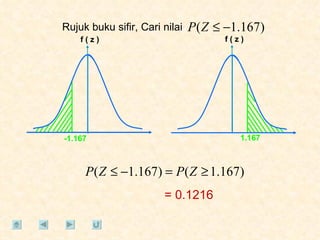
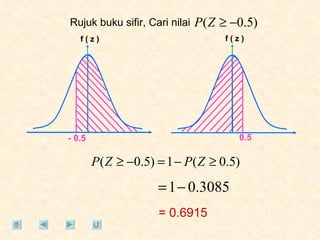
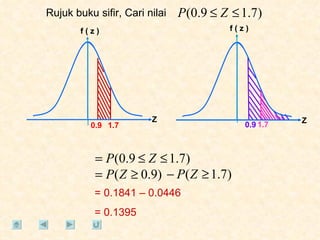
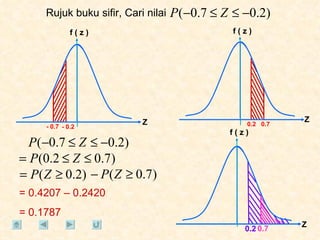
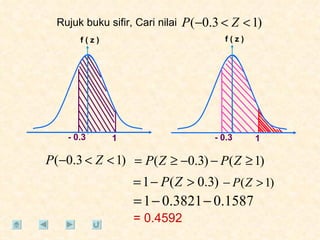
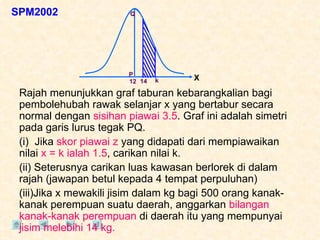
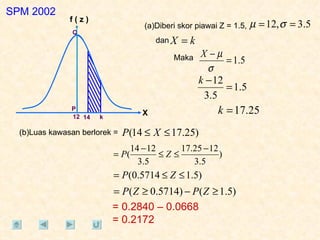
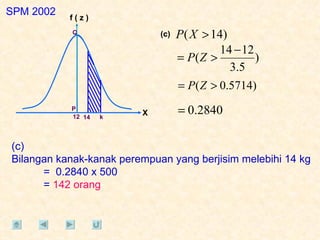
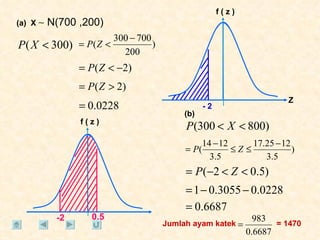
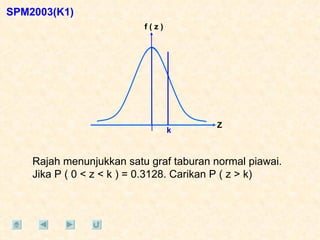
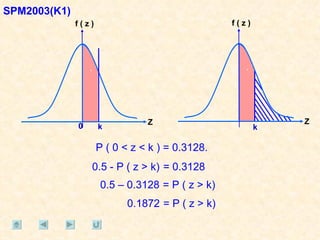
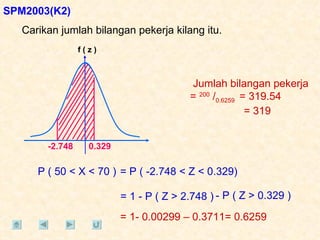
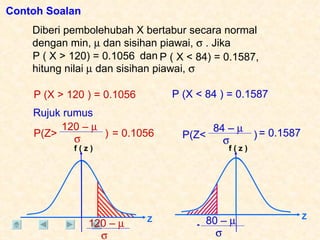
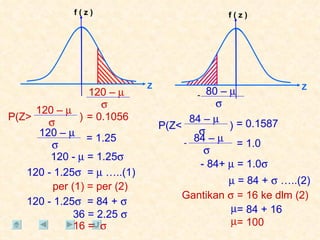
Dokumen tersebut membahas tentang taburan normal, probabilitas, dan penyelesaian soal-soal statistika yang melibatkan konsep-konsep tersebut. Beberapa soal meminta menentukan nilai probabilitas berdasarkan grafik taburan normal dan rumus-rumus yang terkait.

1. ditulis Z  N( 0,1) X ditukar kepada Z (skor piawai) ditulis Z bertabur secara normal piawai 0 Taburan Normal Kepada Taburan Normal Piawai X bertabur secara normal dengan min , dan sisihan piawai X  N( , ) (rujuk rumus) X f ( x ) Z f ( z )

2. 1 P(Z ≥ 1) = 0.1587 Rujuk buku sifir, Cari nilai Z f ( z )

3. = 0.1216 -1.167 1.167 Rujuk buku sifir, Cari nilai f ( z ) f ( z )

4. = 0.6915 Rujuk buku sifir, Cari nilai 0.5 - 0.5 f ( z ) f ( z )

5. Rujuk buku sifir, Cari nilai = 0.1841 – 0.0446 = 0.1395 0.9 0.9 1.7 1.7 Z f ( z ) Z f ( z )

6. Rujuk buku sifir, Cari nilai = 0.4207 – 0.2420 = 0.1787 0.2 - 0.7 - 0.2 0.2 0.7 0.7 Z f ( z ) Z f ( z ) Z f ( z )

7. Rujuk buku sifir, Cari nilai = 0.4592 - 0.3 - 0.3 1 1 f ( z ) f ( z )

8. SPM2002 Rajah menunjukkan graf taburan kebarangkalian bagi pembolehubah rawak selanjar x yang bertabur secara normal dengan sisihan piawai 3.5 . Graf ini adalah simetri pada garis lurus tegak PQ. (i) Jika skor piawai z yang didapati dari mempiawaikan nilai x = k ialah 1.5 , carikan nilai k. (ii) Seterusnya carikan luas kawasan berlorek di dalam rajah (jawapan betul kepada 4 tempat perpuluhan) (iii)Jika x mewakili jisim dalam kg bagi 500 orang kanak-kanak perempuan suatu daerah, anggarkan bilangan kanak-kanak perempuan di daerah itu yang mempunyai jisim melebihi 14 kg. X k 12 P Q 14

9. SPM 2002 k 14 12 P Q = 0.2840 – 0.0668 = 0.2172 Maka (a)Diberi skor piawai Z = 1.5, dan (b)Luas kawasan berlorek = X f ( z )

10. SPM 2002 (c) Bilangan kanak-kanak perempuan yang berjisim melebihi 14 kg = 0.2840 x 500 = 142 orang (c) X k 14 12 P Q f ( z )

11. SPM2001 Jisim ayam katek di sebuah ladang adalah mengikut taburan normal dengan min 700g dan sisihan piawai 200g . Jika seekor ayam katek dipilih secara rawak, hitungkan kebarangkalian bahawa jisimnya (i) kurang daripada 300g (ii) antara 300g dan 800g Seterusnya jika terdapat 983 ekor ayam katek yang jisimnya antara 300g dan 800g , anggarkan jumlah ayam katek di ladang itu.

12. (a) X  N(700 ,200) (b) Jumlah ayam katek = 1470 0.5 -2 f ( z ) Z - 2 f ( z )

13. SPM2003(K1) Rajah menunjukkan satu graf taburan normal piawai. Jika P ( 0 < z < k ) = 0.3128. Carikan P ( z > k) Z k f ( z )

14. SPM2003(K1) Z k f ( z ) P ( 0 < z < k ) = 0.3128. 0.5 - P ( z > k) 0 = 0.3128 = P ( z > k) 0.5 – 0.3128 = P ( z > k) 0.1872 Z f ( z ) k

15. Jisim bagi pekerja di sebuah kilang bertabur normal dengan Carikan jumlah bilangan pekerja kilang itu. SPM2003(K2) min 67.86 kg dan varians 42.25 kg 2 . 200 orang pekerja kilang itu mempunyai jisim antara 50kg dengan 70kg. Menukarkan X kepada Z (Rujuk rumus) X = 50 X = 70 Z = - 2.7477 Z = 0.32923 P ( 50 < X < 70 ) = P ( -2.748 < Z < 0.329 ) Z = 50 – 67.86 6.5 Z = 70 – 67.86 6.5

16. Carikan jumlah bilangan pekerja kilang itu. SPM2003(K2) P ( 50 < X < 70 ) = P ( -2.748 < Z < 0.329) 0.329 -2.748 = 1 - P ( Z > 2.748 ) - P ( Z > 0.329 ) = 1- 0.00299 – 0.3711= 0.6259 Jumlah bilangan pekerja = 200 / 0.6259 = 319.54 = 319 f ( z )

17. Diberi pembolehubah X bertabur secara normal dengan min,  dan sisihan piawai,  . Jika dan hitung nilai  dan sisihan piawai,  Contoh Soalan P ( X > 120) = 0.1056 P (X > 120 ) = 0.1056 P ( X < 84) = 0.1587, P (X < 84 ) = 0.1587 Rujuk rumus = 0.1056 = 0.1587 P(Z> ) 120 –   P(Z< ) 84 –   Z 120 –   f ( z ) f ( z ) Z 80 –   -

18. = 0.1056 = 0.1587 = 1.25 = 1.0 120 -  = 1.25  120 - 1.25  =  …..(1) - 84+  = 1.0   = 84 +  …..(2) per (1) = per (2) 120 - 1.25  = 84 +  36 = 2.25  16 =  Gantikan  = 16 ke dlm (2) = 84 + 16 = 100 P(Z> ) 120 –   P(Z< ) 84 –   Z 120 –   Z 80 –   - 120 –   84 –   - f ( z ) f ( z )