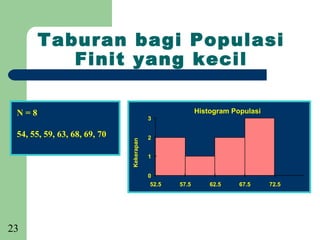
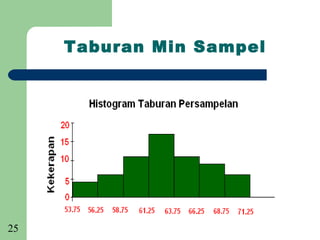
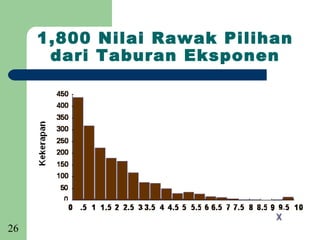
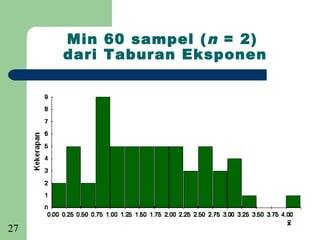
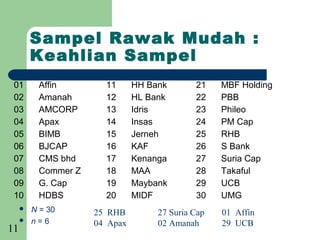
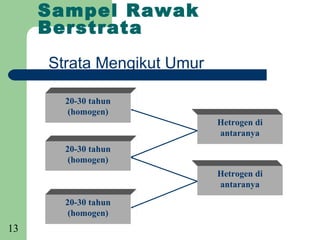
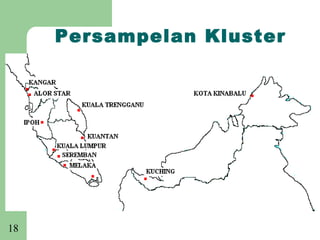
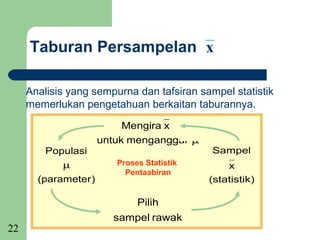
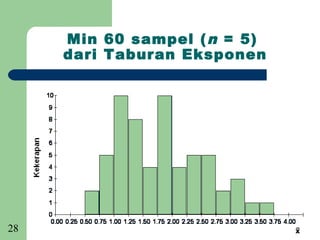
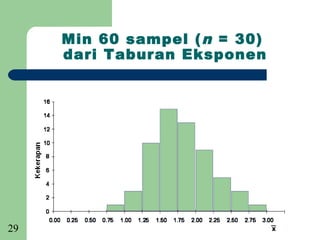
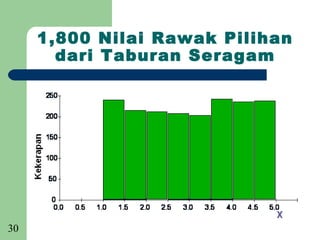
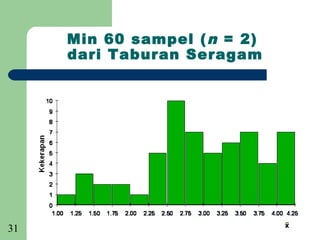
[Ringkasan] Dokumen tersebut membincangkan mengenai persampelan dan taburan. Ia menjelaskan beberapa sebab utama mengapa persampelan diperlukan seperti untuk menjimatkan wang dan masa, memperluaskan skop data apabila sumber terhad, dan menyelamatkan keluaran kerana proses penyelidikan kadangkala merosakkan. Dokumen ini juga membincangkan beberapa teknik persampelan seperti rawak mudah, rawak berstrata, sistematik

1. Persampelan dan Taburan
Persampelan
1

2. Sebab Membuat
Persampelan
 Persampelan boleh menjimatkan wang.
 Persampelan boleh menjimatkan masa.
 Untuk sumber yang terhad, persampelan
boleh memperluaskan skop set data.
 Disebabkan proses penyelidikan kadangkala
merosakkan, sampel dapat menyelamatkan
keluaran.
 Jika memperolehi populasi adalah mustahil,
persampelan adalah alternatif yang sesuai.
2

3. Sebab Membuat
Bancian
 Menghapuskan kemungkinan sampel rawak
tidak mewakili populasi.
 Mereka yang berkuasa dalam kajian tidak
selesa dengan maklumat sampel.
3

4. Kerangka Populsi
 Kerangka  senarai populasi, peta, direktori, atau lain-lain
sumber yang boleh digunakan untuk mewakili
populasi
 Kerangka daftar lebih  mengandungi semua unit
populasi sasaran ditambah dengan unit tambahan.
CONTOH: menggunakan senarai keahlian dewan
perniagaan sebagai kerangka untuk sasaran populasi
ahli perniagaan wanita.
 Kerangka daftar kurang  mengandungi unit yang kurang
daripada populasi sasaran.
Contoh: menggunakan senarai keahlian dewan perniagaan
sebagai kerangka untuk sasaran populasi semua ahli
4 perniagaan

5. Persampelan Rawak vs Tidak
Rawak
Persampelan Rawak
 setiap unit di dalam populasi mempunyai
kebarangkalian yang sama untuk dipilih sebagai
sampel.
 Mekanisma peluang digunakan didalam proses
pemilihan.
 Bias dihapuskan didalam proses pemilihan.
 Dikenali sebagai persampelan berkebarangkalian
5

6. Persampelan Rawak vs Tidak
Rawak
Persampelan Tidak Rawak
 Tidaksemua unit populasi mempunyai
kebarangkalian untuk dipilih kedalam sampel.
 Terbuka untuk bias pemilihan
 Kaedah pemilihan data tidak bersesuaian
bagi kebanyakan kaedah statistik
 Dikenali sebagai persampelan tidak
berkebarangkalian
6

7. Teknik Persampelan
Rawak
 Sampel Rawak Mudah
 Sampel Rawak Berstrata
– Berkadaran
– Tidak Berkadaran
 Sampel Rawak Sistematik
 Persampelan Kluster (atau Kawasan)
7

8. Sampel Rawak Mudah
 Nomborkan setiap unit dalam kerangka dari
1 hingga N.
 Gunakan jadual nombor rawak atau penjana
nombor rawak untuk memilih n nombor yang
berbeza diantara 1 hingga N.
 Mudah untuk dibentuk untuk populasi yang
kecil
 Mengelirukan untuk populasi yang besar
8

9. Sampel Rawak Mudah :
Nomborkan Kerangka
Populasi
01 Affin 11 HH Bank 21 MBF Holding
02 Amanah 12 HL Bank 22 PBB
03 AMCORP 13 Idris 23 Phileo
04 Apax 14 Insas 24 PM Cap
05 BIMB 15 Jerneh 25 RHB
06 BJCAP 16 KAF 26 S Bank
07 CMS bhd 17 Kenanga 27 Suria Cap
08 Commer Z 18 MAA 28 Takaful
09 G. Cap 19 Maybank 29 UCB
10 HDBS 20 MIDF 30 UMG
9

10. Sampel Rawak Mudah :
Jadual Nombor Rawak
91567 42595 27958 30134 04024 86385 29880 99730
46503 18584 18845 49618 02304 51038 20644 58727
34914 63976 88720 82765 34476 17032 87589 40836
57491 16703 23167 49323 45021 33132 12544 41035
30405 83946 23792 14422 15059 45799 22716 19792
09983 74353 68668 30429 70735 25499 16631 35006
85900 07119 97336 71048 08178 77233 13916 47564
 N = 30
 n=6
10

11. Sampel Rawak Mudah :
Keahlian Sampel
01 Affin 11 HH Bank 21 MBF Holding
02 Amanah 12 HL Bank 22 PBB
03 AMCORP 13 Idris 23 Phileo
04 Apax 14 Insas 24 PM Cap
05 BIMB 15 Jerneh 25 RHB
06 BJCAP 16 KAF 26 S Bank
07 CMS bhd 17 Kenanga 27 Suria Cap
08 Commer Z 18 MAA 28 Takaful
09 G. Cap 19 Maybank 29 UCB
10 HDBS 20 MIDF 30 UMG
 N = 30 25 RHB 27 Suria Cap 01 Affin
 n=6 04 Apax 02 Amanah 29 UCB
11

12. Sampel Rawak
Berstrata
 populasi adalah dibahagikan kepada sub-populasi
yang tidak bertindih dipanggil sebagai starata.
 memilih sampel rawak mudah dari setiap sub-populasi.
 Berpontensi untuk mengurangkan ralat persampelan
 Berkadaran  peratus sampel diambil dari setiap
strata adalah berkadaran dengan peratus dimana
setiap strata didalam populasi
 Tidak Berkadaran  bahagian strata dikalangan sampel
adalah berbeza dari bahagian strata diantara populasi
12

13. Sampel Rawak
Berstrata
Strata Mengikut Umur
20-30 tahun
(homogen)
Hetrogen di
antaranya
20-30 tahun
(homogen)
Hetrogen di
antaranya
20-30 tahun
(homogen)
13

14. Persampelan Sistematik
 Selesa dan relatif mudah untuk N
k = ,
ditadbirkan. n
 Unsur-unsur populasi adalah dimana
:
disusun berturutan .
n = saiz sampel
 Unsur sampel pertama adalah
N = saiz populasi
dipilih secara rawak dari unsur
k populasi yang pertama. k = size selang yang dipilih
 Kemudian, unsur sampel adalah
dipilih pada selang tetap, k, dari
susunan turutan kerangka.
14

15. Persampelan Sistematik
: Contoh
 Pesanan belian untuk tahun lepas diberi nombor siri 1
hingga 10,000 (N = 10,000).
 Sampel lima puloh (n = 50) pesanan belian adalah
diperlukan untuk diaudit.
 k = 10,000/50 = 200
 Unsur sampel pertama dipilih secara rawak dari 200
pesanan belian yang pertama. Andaikan pesanan belian
yang ke 45 adalah dipilih.
 Turutan unsur sampel: 245, 445, 645, . . .
15

16. Persampelan Kluster
 Melibatkan pembahagian populasi kepada
kawasan atau kluster yang tidak bertindih
 Subset kluster adalah dipilih secara rawak
sebagai sampel.
 Jika bilangan unsur didalam subset kluster
adalah lebih besar dari nilai n yang diperlukan,
kluster ini kemudiannya dibahagikan untuk
membentuk set kluster yang baru dan tertaakluk
kepada proses pemilihan rawak
16

17. Persampelan Kluster
Kebaikan
• Lebih selesa untuk populasi bercorak geografi
• Mengurangkan kos perjalanan untuk menemui unsur sampel
• Pentabiran survei yang mudah
• Ketiadaan kerangka persampelan menghalang penggunaan
kaedah persampelan rawak yang lain
Kelemahan
•Kurang cekap dari segi statistik apabila unsur kluster
adalah samar
•Kod dan masalah analisis statistik adalah lebih besar
17 berbanding persampelan rawak mudah

18. Persampelan Kluster
18

19. Persampelan Tidak
Rawak
 Persampelan selesa: unsur sampel dalah diambil
mengikut keselesaan penyelidik
 Persampelan Pertimbangan: unsur sampel adalah
dipilih melalui pertimbangan penyelidik
Persampelan Kouta: unsur sampel adalah diambil
sehingga kawalan kouta dipenuhi
Persampelan bola salji: subjek survei adalah dipilih
berdasarkan kepada rujukan survei responden yang lain
19

20. Ralat
Data dari sampel tidak rawak adalah
tidak sesuai untuk dianalisis oleh
kaedah statistik pentaabiran.
Ralat Persampelan terjadi apabila
sampel tidak mewakili populasi
20

21. Ralat
Ralat Bukan Persampelan
• Missing Data, Recording, Data Entry, and
Analysis Errors
• Konsep yang lemah, definasi tidak jelas,
dan soal selidik yang mengelirukan
• Ralat jawapan terjadi apabila responden tidak
tahu, tidak menjawab, atau jawapan yang
mengelirukan
21

22. Taburan Persampelan x
Analisis yang sempurna dan tafsiran sampel statistik
memerlukan pengetahuan berkaitan taburannya.
Mengira x
untuk menganggar µ
Populasi Sampel
µ Proses Statistik x
Pentaabiran
(parameter ) (statistik)
Pilih
sampel rawak
22

23. Taburan bagi Populasi
Finit yang kecil
N=8 Histogram Populasi
3
54, 55, 59, 63, 68, 69, 70 Kekerapan 2
1
0
52.5 57.5 62.5 67.5 72.5
23

24. Ruang Sampel untuk n = 2
dengan Penggantian
Sampel Min Sampel Min Sampel Min Sampel Min
1 (54,54) 54.0 17 (59,54) 56.5 33 (64,54) 59.0 49 (69,54) 61.5
2 (54,55) 54.5 18 (59,55) 57.0 34 (64,55) 59.5 50 (69,55) 62.0
3 (54,59) 56.5 19 (59,59) 59.0 35 (64,59) 61.5 51 (69,59) 64.0
4 (54,63) 58.5 20 (59,63) 61.0 36 (64,63) 63.5 52 (69,63) 66.0
5 (54,64) 59.0 21 (59,64) 61.5 37 (64,64) 64.0 53 (69,64) 66.5
6 (54,68) 61.0 22 (59,68) 63.5 38 (64,68) 66.0 54 (69,68) 68.5
7 (54,69) 61.5 23 (59,69) 64.0 39 (64,69) 66.5 55 (69,69) 69.0
8 (54,70) 62.0 24 (59,70) 64.5 40 (64,70) 67.0 56 (69,70) 69.5
9 (55,54) 54.5 25 (63,54) 58.5 41 (68,54) 61.0 57 (70,54) 62.0
10 (55,55) 55.0 26 (63,55) 59.0 42 (68,55) 61.5 58 (70,55) 62.5
11 (55,59) 57.0 27 (63,59) 61.0 43 (68,59) 63.5 59 (70,59) 64.5
12 (55,63) 59.0 28 (63,63) 63.0 44 (68,63) 65.5 60 (70,63) 66.5
13 (55,64) 59.5 29 (63,64) 63.5 45 (68,64) 66.0 61 (70,64) 67.0
14 (55,68) 61.5 30 (63,68) 65.5 46 (68,68) 68.0 62 (70,68) 69.0
15 (55,69) 62.0 31 (63,69) 66.0 47 (68,69) 68.5 63 (70,69) 69.5
16 (55,70) 62.5 32 (63,70) 66.5 48 (68,70) 69.0 64 (70,70) 70.0
24

25. Taburan Min Sampel
25

26. 1,800 Nilai Rawak Pilihan
dari Taburan Eksponen
26

27. Min 60 sampel ( n = 2)
dari Taburan Eksponen
27

28. Min 60 sampel ( n = 5)
dari Taburan Eksponen
28

29. Min 60 sampel ( n = 30)
dari Taburan Eksponen
29

30. 1,800 Nilai Rawak Pilihan
dari Taburan Seragam
30

31. Min 60 sampel ( n = 2)
dari Taburan Seragam
31

32. Min 60 sampel ( n = 5)
dari Taburan Seragam
32

33. Min 60 sampel ( n = 30)
dari Taburan Seragam
33

34. Teoram Had Memusat
Mencukupi bagi saiz sampel yang besar (n ≥ 30),
 Taburan min sampel x , adalah menghampiri normal,
 min taburan ini adalah sama dengan µ, min untuk populasi
 Sisihan piawai ialah σ ,n
 Bergantung kepada bentuk taburan populasi
34

35. Teoram Had Memusat
Jika x ialah min sampel rawak bersaiz n
dari populasi dengan min µ dan sisihan
piawai σ, maka apabila n meningkat
(n ≥ 30) taburan x menghampiri taburan
normal dengan min µx = µ dan sisihan
σ
piawai σx = n
.
35

36. Persampelan dari
Populasi Normal
 Taburanbagi min sampel adalah bertaburan
normal bagi sebarang saiz sampel.
Jika x adalah min sampel rawak bersaiz n
dari populasi normal dengan min µ dan
sisihan piawai σ, taburan x adalah bertaburan
normal dengan min µ = µ dan
x
σ
sisihan piawai σ x = .
36
n

37. Taburan Min Sampel bagi
Berbagai Saiz Sampel
37

38. Formula Z Formula untuk Min
Sampel
X −µ
Z= X
σX
X −µ
=
σ
n
38

39. Contoh
Katakan min perbelanjaan saorang pelanggan dipasar raya ialah
RM85.00, dengan sisihan piawai RM9.00. Jika sampel rawak 40
pelanggan diambil, apakah kebarangkalian purata sampel
perbelanjaan per pelanggan bagi sampel ini adalah RM87.00 atau
lebih?
µ = RM85.00, σ = RM9.00, n = 40
 
 
 X - µX  X-µ 
P( X ≥ 87) = P Z ≥  = P Z≥ = P(Z  1.41)
 σX    σ 
    
  n 
= 0.50 – 0.4201
RM87.00 - RM85.00 RM2.00
= = = 1.41
 RM9.00  RM1.42 = 0.0793
 
 40 
39

40. Penyelesaian Secara
Geraf
X - µ 87 − 85 2 Keluasan sama
Z= = = = 1. 41 of .0793
σ 9 1. 42
40 n 40

41. Contoh 7.1
Katakan dalam sata satu jam di dalam pasaraya yang besar,
purata bilangan pelanggan ialah 448, dengan sisihan piawai
21 pelanggan. Apakah kebarangkalian sampel rawak 49 jam
membeli belah yang berbeza akah menghasilkan min sampel
antara 441 dan 446 pelanggan?
µ = 448, σ = 21, dan n = 49.
P(441 ≤ X ≤ 446) = ?
41

42. X - µ 441 − 448 X - µ 446 − 448
Z= = = − 2.33 Z= = = − 0.67
σ 21 σ 21
n 49 n 49
P(-2.33  Z  -0.67) = 0.4901 – 0.2486
42 = 0.2415

43. Persampelan dari
Populasi Finit tanpa
Penggantian
 Di dalam kes ini, sisihan piawai taburan min sampel
adalah lebih kecil apabila persampelan dari populasi
tidak finit (atau dari populasi finit dengan penggantian).
 Nilai yang benar bagi sisihan piawai ini adalah dikira
dengan menggunakan faktor pembetulan finit terhadap
sisihan piawai untuk persampelan dari populasi bukan
finit.
 Jika saiz sampel kurang dari 5% saiz populasi,
pelarasan adalah tidak perlu.
43

44. Persampelan dari Populasi
Finit
N-n
Faktor Pembetulan Finit =
N -1
X -µ
Formula Z diubahsuai = Z =
σ N-n
n N -1
44

45. Faktor Pembetulan Finit
untuk Beberapa Saiz Sampel
45

46. Contoh
Syarikat pengeluaran mempunyai 350 jam pekerja
dengan purata umur 37.6 tahun dengan sisihan piawai
8.3 tahun. Jika sampel rawak 45 jam pekerja diambil,
apakah kebarangkalian sempel tersebut mempunyai
purata umur kurang daripada 40 tahun?
µ = 37.6, σ = 8.3, n = 45 dan N = 350.
P( X ≤ 40) = ?
46

47. 0.500 0.4808
 
 
Z ≤ X -µ 
µ=37.6 X = 40
P( X ≤ 40) = P Z=0 Z=2.07
 σ N-n 
 
 n N -1 
40.0 - 37.6 2.4
Z= = = 2.07
 8.3   350 - 45 
 
1.157

 

 45   350 - 1 
 
P( Z ≤ 2.07) = 0.5000 + 0.4808 = 0.9808
47

48. 
Taburan Persampelan p
 Perkadaran Sampel
X
p=
ˆ
n
dim ana :
X = bilangan item di dalam sampel yang mempunyai ciri - ciri yang dikehendaki
n = bilangan item di dalam sampel
Taburan Persampelan
• Penghampiran normal jika nP > 5 and nQ > 5 (P
adalah perkadaran populasi dan Q = 1 - P.)
• Min bagi taburan ialah P.
• Sisihan piawai taburan ialah P ⋅ Q
n
48

49. Formula Z untuk Perkadaran
Sampel
p-P
Z=
P.Q
n
dimana
_
p = perkadaran sampel
n = saiz sampel
P = perkadaran populasi
49 Q=1-P

50. Contoh
Katakan 60% kontraktor elektrik di Serdang menggunakan jenama
dawai elektrik tertentu. Apakah kebarangkalian mengambil sampel
rawak bersaiz 120 daripada kontraktor elektrik tersebut dan
mendapati 0.50 atau kurang menggunakan jenama dawai elektrik
tersebut?
_
P = 0.60 , P( p  0.50), n = 120 dan Q = 1 – P = 0.40
 
 
0.50 - P 
P( p ≤ 0.50) = P Z ≤
 P.Q 
 
 n 
0.50 - 0.60 - 0.10
= = = - 2.24
(0.60)(0.40) 0.0447
50 120

51. 0.4875
^ = 0.50
p P=0.60
Z=-2.24 Z=0
P(p  0.50) = P( Z  -2.24) = 0.5000 – 0.4875
51

52. 52