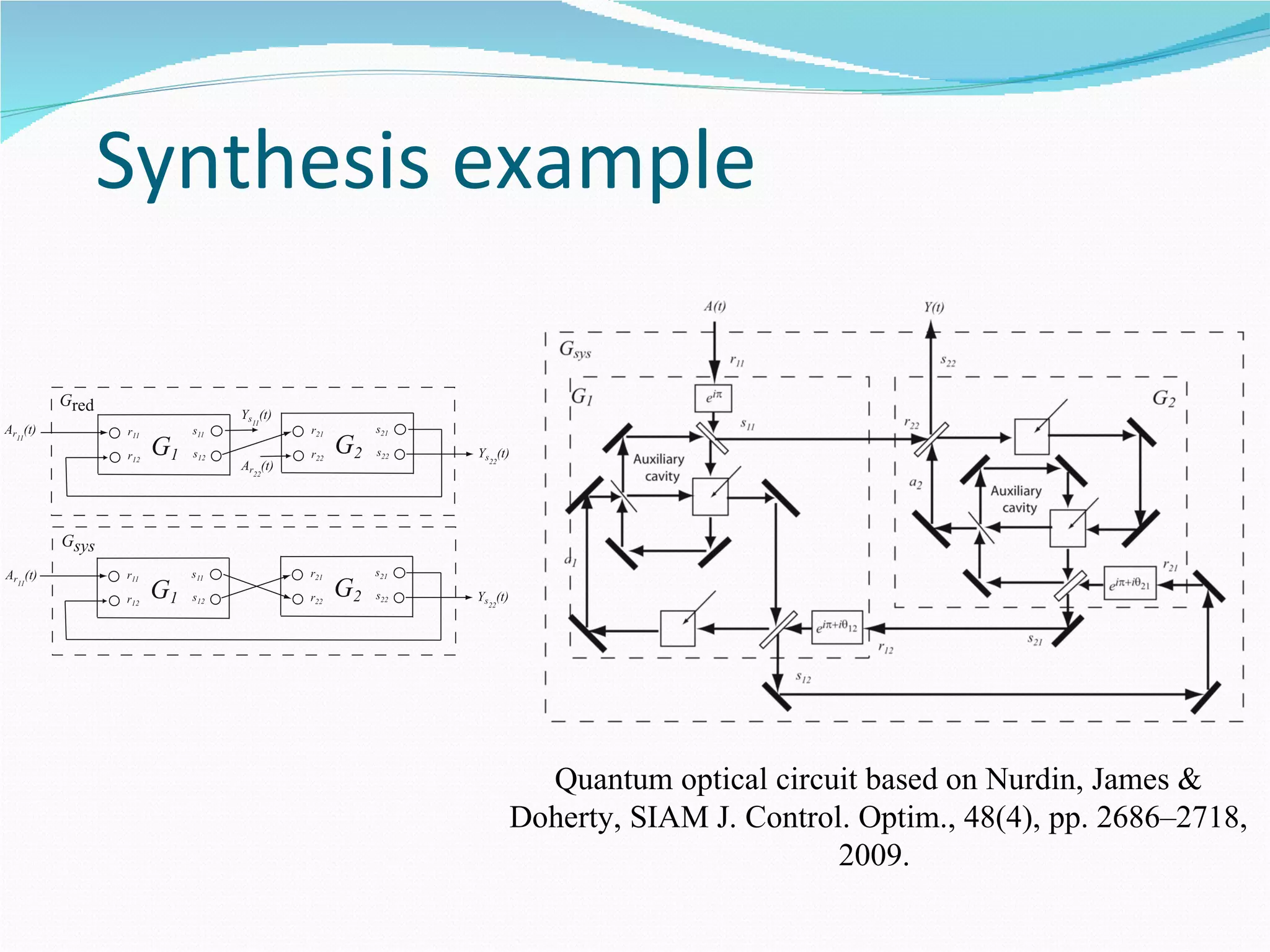
1. The document outlines a method for synthesizing linear quantum stochastic systems using quantum feedback networks. Small time delays allow approximating direct interactions with field-mediated interactions. 2. As an example, a quantum optical circuit is synthesized based on earlier work. Components are interconnected to approximate a desired system dynamics for small time delays. 3. In conclusion, linear quantum systems can be approximately synthesized by quantum feedback networks for small time delays, using field-mediated interactions to simulate direct interactions. Additional results are available in another paper.

1. Hendra I. Nurdin (ANU) TexPoint fonts used in EMF. Read the TexPoint manual before you delete this box.: A A

2. Outline of talk Quick reminder: Linear quantum stochastic systems Synthesis via quantum feedback networks Synthesis example Concluding remarks

3. Linear quantum stochastic systems An (Fabry-Perot) optical cavity Non-commuting Wiener processes Quantum Brownian motion

4. Linear quantum stochastic systems x = ( q 1 ,p 1 ,q 2 ,p 2 ,…, q n ,p n ) T A 1 = w 1 +iw 2 A 2 = w 3 +iw 4 A m =w 2m-1 +iw 2m Y 1 = y 1 + i y 2 Y 2 = y 3 + i y 4 Y m’ = y 2m’-1 + i y 2m’ S Quadratic Hamiltonian Linear coupling operator Scattering matrix S B 1 B 2 B m

5. Synthesis of linear quantum systems “ Divide and conquer” – Construct the system as a suitable interconnection of simpler quantum building blocks, i.e., a quantum network, as illustrated below: Wish to realize this system ( S , L , H ) ? ? ? ? ? ? Network synthesis Quantum network Input fields Output fields Input fields Output fields

6. An earlier synthesis theorem The G j ’s are one degree (single mode) of freedom oscillators with appropriate parameters determined using S , L and H. The H jk ’s are certain bilinear interaction Hamiltonian between G j and G k determined using S , L, and H. Nurdin, James & Doherty, SIAM J. Control. Optim., 48(4), pp. 2686–2718, 2009. G 1 G 2 G 3 G n H 12 H 23 H 13 H 2n H 3n H 1n G = ( S , L , H ) A(t) y(t)

7. Realization of direct coupling Hamiltonians Many-to-many quadratic interaction Hamiltonian can be realized, in principle, by simultaneously implementing the pairwise quadratic interaction Hamiltonians { H jk }, for instance as in the configuration shown on the right. Complicated in general, are there alternatives?

8. Quantum feedback networks

9. Quantum feedback networks Quantum feedback networks are not Markov due to the time delays for propagation of fields. In the limit as all time delays go to zero one can recover an effective reduced Markov model (Gough & James, Comm. Math. Phys., 287, pp. 1109–1132, 2009).

10. Approximate direct interaction via field-mediated interactions Idea: Use field-mediated feedback connections to approximate a direct interaction for small time delays. Feedback interconnections to approximate direct interactions

11. Model matrix

12. Concatenated model matrix In channel 1 In channel 2 Out channel 1 Out channel 2

13. Connecting input and output, and reduced Markov model (Out channel 1 connected to In channel 2) (Series product) Gough & James, Comm. Math. Phys. , 287, pp. 1109–1132, 2009; IEEE-TAC , 54(11), pp. 2530–2544, 2009

14. Synthesis via quantum feedback networks Suppose we wish to realize G sys =( I , L , H ) with and Let G jk = ( S jk , L jk , 0) for j ≠ k, and G jj = ( I, K j x j , ½ x j T R j x j ), for j , k = 1 , …, n , with L jk and R j to be determined, L jk =K jk x j having multiplicity 1, and S jk a complex number with | S jk |=1.

15. Synthesis via quantum feedback networks Define G j , j= 1,…, n, and G as in the diagram below:

16. Synthesis via quantum feedback networks Summary of results: One can always find L jk , S jk ( j ≠ k ) and R j such that when the output field associated with L jk is connected to the input field associated with L kj , for all j , k =1, …, n and j ≠ k , and for small time delays in these connections, then G as constructed approximates G sys . L jk , S jk , and R j can be computed explicitly. In the limit of zero time delays the interconnections via L kj and L jk ( j ≠ k ) realizes the direct interaction Hamiltonian H jk =x j T R jk x k .

17. Synthesis example

18. Synthesis example Quantum optical circuit based on Nurdin, James & Doherty, SIAM J. Control. Optim., 48(4), pp. 2686–2718, 2009.

19. Concluding remarks Linear quantum stochastic systems can be approximately synthesized by a suitable quantum feedback network for small time delays between interconnections. Main idea is to approximate direct interaction Hamiltonians by field-mediated interconnections. Direct interactions and field-mediated interactions can be combined to form a hybrid synthesis method. Additional results available in: H. I. Nurdin, “Synthesis of linear quantum stochastic systems via quantum feedback networks,” accepted for IEEE-TAC, preprint: arXiv:0905.0802, 2009.

20. That’s all folks THANK YOU FOR LISTENING!

21. From linear quantum stochastic systems to cavity QED systems Linear quantum stochastic system Cavity QED system