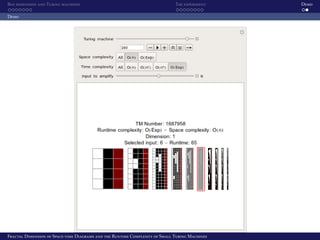
This document discusses the relationship between the fractal dimension of space-time diagrams and the runtime complexity of small Turing machines, focusing on machines with varying states and colors. It presents experimental findings and methodologies applied to compute the box dimension of Turing machines, including notable results for machines running in polynomial and exponential time. Key results indicate that in the (3,2) space, the conjectured upper bounds hold true and relationships between dimensionality and computation time are established.