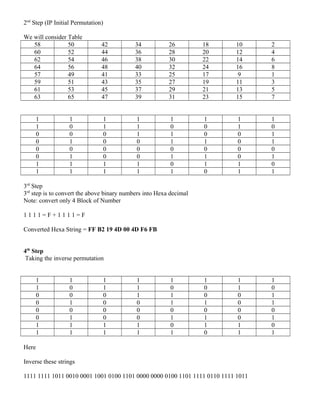
The document discusses fundamental concepts of information security, including security mechanisms, services, and attacks, with examples of encryption techniques such as the Caesar cipher, Playfair cipher, and DES algorithm. It explains the mathematical equations used for encoding and decrypting messages, highlighting the time complexity associated with different key sizes for encryption. The document provides examples and methodologies for these cryptographic techniques and their applications.

1. Basic Security Issues
• Mechanism
• Services
• Attack
3 Aspect of Information Security
• Security Mechanism
• Security Services
• Security Attack
Ceaser Cipher
Cease Cipher Manipulate the Character with 3 positions (for example: if we Cipher “A” into Ceaser technique then it should be
“D”)
Formula
C= E(P)
C= (P+3) mod26
C= (P+K) mod26
C= Answer
Where C= Cipher
P= Plain Text
E= Encryption
K= Key
Example
P = 81529
0 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10
C=E(P)
C = (P+K) mod10
C = (P+3)mod10
C = (8+3)mod10 = 1
C = (1+3)mod10 = 4
C = (5+3)mod10 = 8
C = (2+3)mod10 = 5
C = (9+3)mod10 = 2
E = 14852
P= MUSTARD
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
E= PXVWDUG

2. Transportation Technique
In Transportation technique we assign fixed range of column, and in that column all the text is entered and encrypt the text with
respect to the column of the row
Example
We are taking 10 Column for the text
P= COMPUTER GRAPHIC MAY BE SLOW BUT ITS EXPENSIVE
1 2 3 4 5 6 7 8 9 10
C O M P U T E R G R
A P H I C M A Y B E
S L O W B U T I T S
E X P E N S I V E Z
E= CAESE OPS MHLE PIOX UCWP T BE EMUN RATS GYII RBTV
Time required at 1 Encryption/ U sec
2^31 U sec = 35.8 min
Key size Number of
Alternative Keys
Time required for 1
encryption
Time required at 10^6
Decryption
32 2^31 = 4.3 x 10^9 2^31usec=35.8 2.15 millisecond
56 2^55 = 7.2 x 10^16 2^55usec=10 hours 10 hours
128 2^127 = 3.4 x 10^38 2^127usec= 5.4x10^18 years
168 2^167 = 3.7 x 10^50 2^167usec= 5.9x 10^30 years
Where
Time Required for 1 encryption for 56 Key size formulated as
2^55
________________
3600 x 10^6 x 10^6
and Time Required for 1 Encryption for 168 keys are formulated as
2^167
____________________
3600 x 10^6 x 10^6 x 365 x 24
Play Fair Cipher
In play fair cipher technique we draw a 5 x 5 matrix and in that matrix the word in encrypted, IN THE REMAINING
COLUMN we add the remaining alphabets

3. Example
Keyword: Monarchy
M O N A R
C H Y B D
E F G I/J K
L P Q S T
U V W X Z
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
AR = (A Converted to the next one that is R and “R” Converted to the next one that is “M”)
AR = RM
MU = (Now Mu belongs to the same column, so “M” will be converted to the next one that is “C” and “U” will be
converted into the next one that is “M”)
MU = CM
HS = ( “H” and “S” belongs to two different column, now we first draw line to “H” row as the Line Intercepts the “B” so
“H” will be converted into B and for “S” we again draw a line as we drew for “H”, As blue line Intercepts on “P” so )
HS = BP
Substitution Technique
DES Algorithm
Des algorithm work on behf of Hexa Decimal Nubers
Plain text= 675a69675e5a6b5a
1st
step
Convert the above number into binary
1234 5678 9-12 13-16 17-20 21-24 25-28 29-32 33-36 37-40 41-44 45-48 49-52 53-56 57-60 61-64
0110 | 0111 | 0101 | 1010 | 0110 | 1001 | 0110 | 0111 | 0101 | 1110 | 0101 | 1010 | 0110 | 1011| 0101 | 1010

4. 2nd
Step (IP Initial Permutation)
We will consider Table
58 50 42 34 26 18 10 2
60 52 44 36 28 20 12 4
62 54 46 38 30 22 14 6
64 56 48 40 32 24 16 8
57 49 41 33 25 17 9 1
59 51 43 35 27 19 11 3
61 53 45 37 29 21 13 5
63 65 47 39 31 23 15 7
1 1 1 1 1 1 1 1
1 0 1 1 0 0 1 0
0 0 0 1 1 0 0 1
0 1 0 0 1 1 0 1
0 0 0 0 0 0 0 0
0 1 0 0 1 1 0 1
1 1 1 1 0 1 1 0
1 1 1 1 1 0 1 1
3rd
Step
3rd
step is to convert the above binary numbers into Hexa decimal
Note: convert only 4 Block of Number
1 1 1 1 = F + 1 1 1 1 = F
Converted Hexa String = FF B2 19 4D 00 4D F6 FB
4th
Step
Taking the inverse permutation
1 1 1 1 1 1 1 1
1 0 1 1 0 0 1 0
0 0 0 1 1 0 0 1
0 1 0 0 1 1 0 1
0 0 0 0 0 0 0 0
0 1 0 0 1 1 0 1
1 1 1 1 0 1 1 0
1 1 1 1 1 0 1 1
Here
Inverse these strings
1111 1111 1011 0010 0001 1001 0100 1101 0000 0000 0100 1101 1111 0110 1111 1011