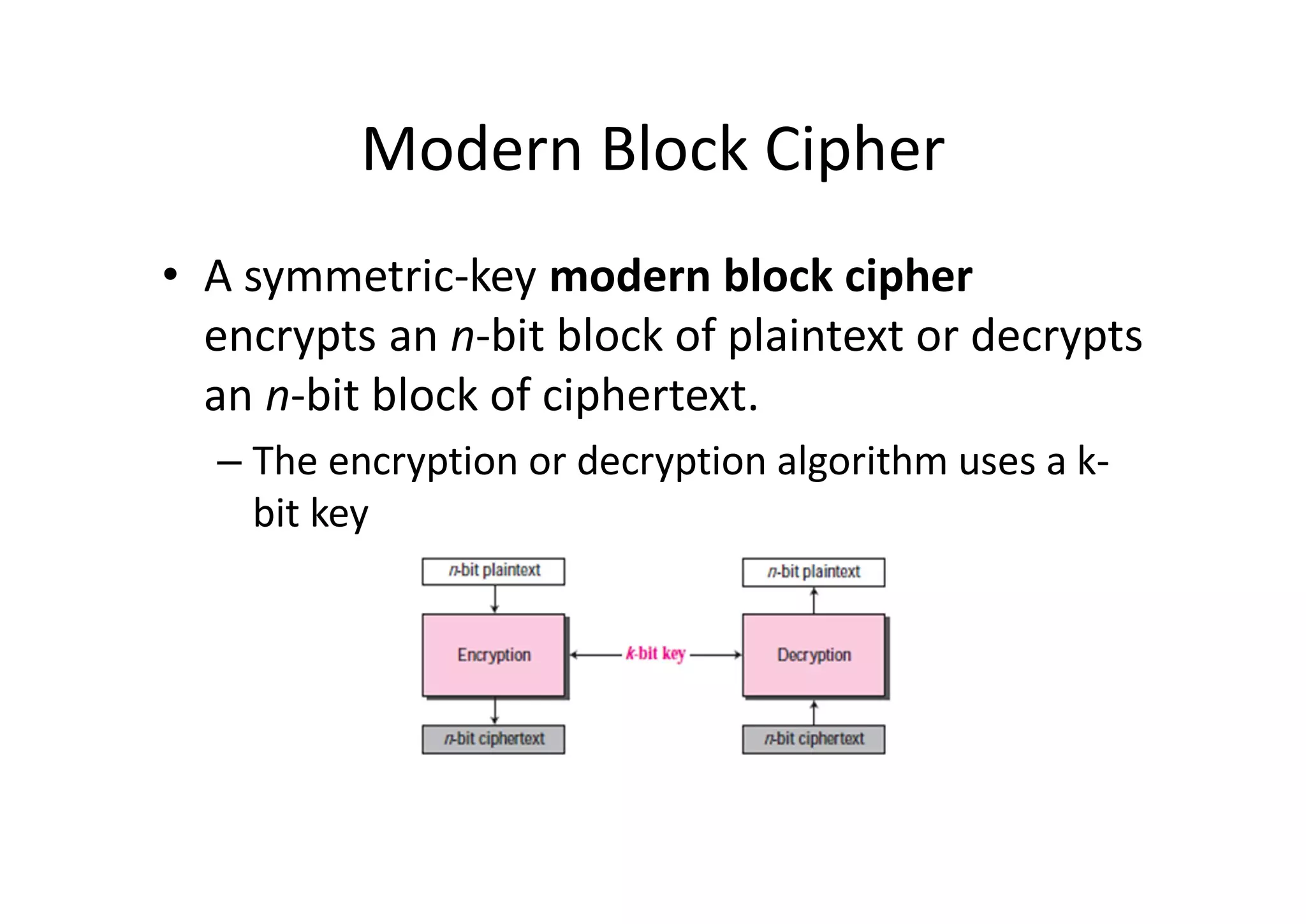
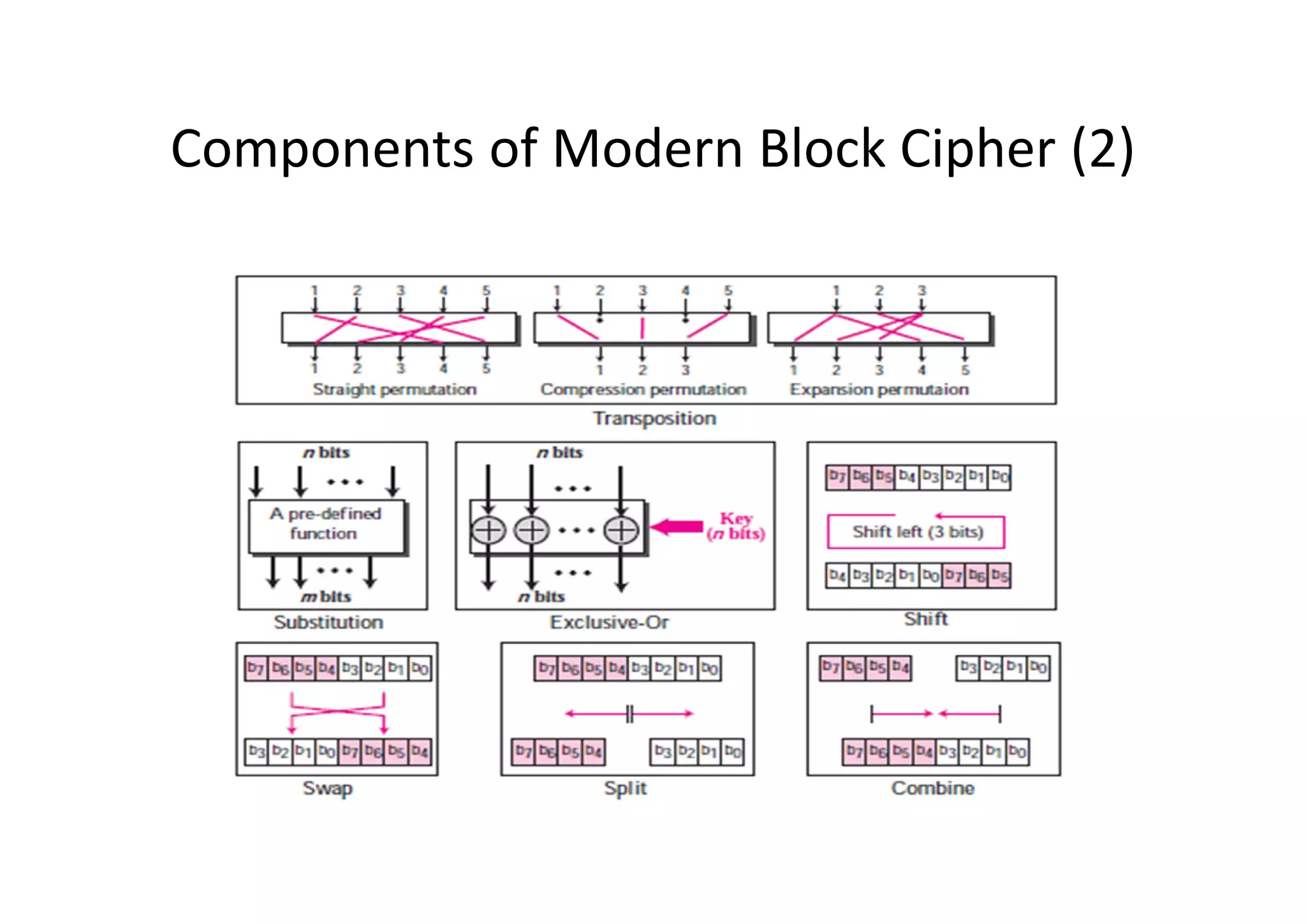
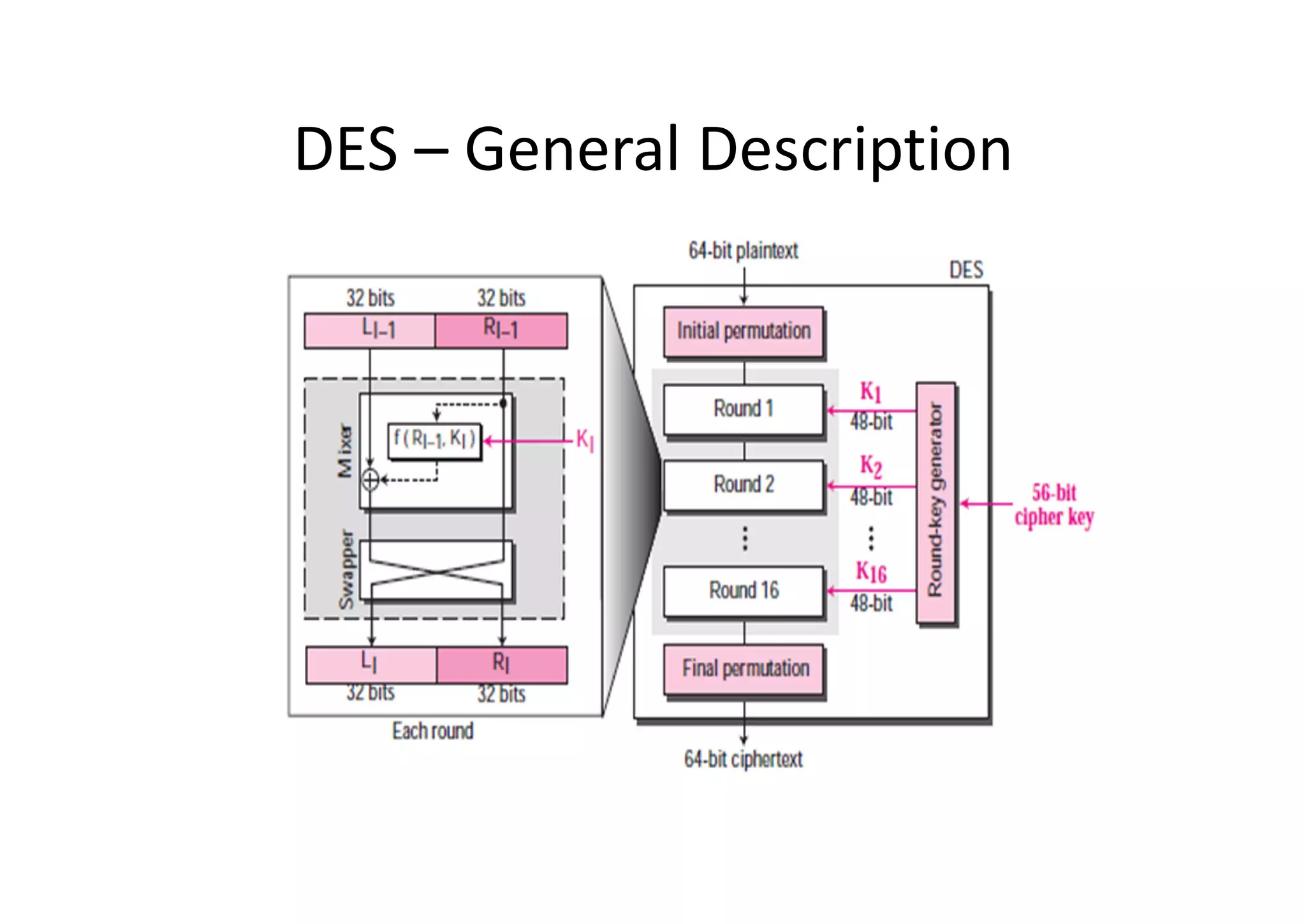
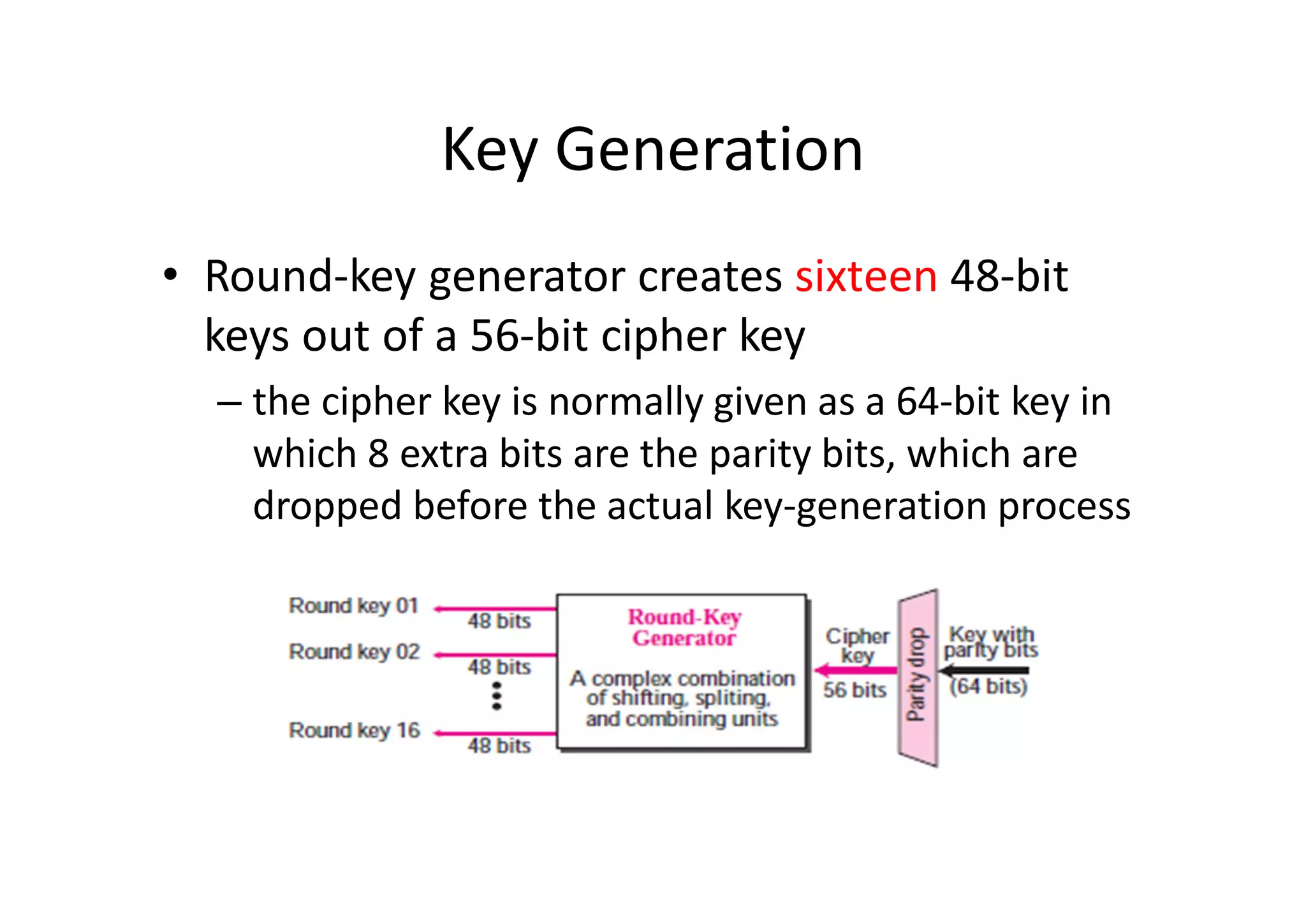
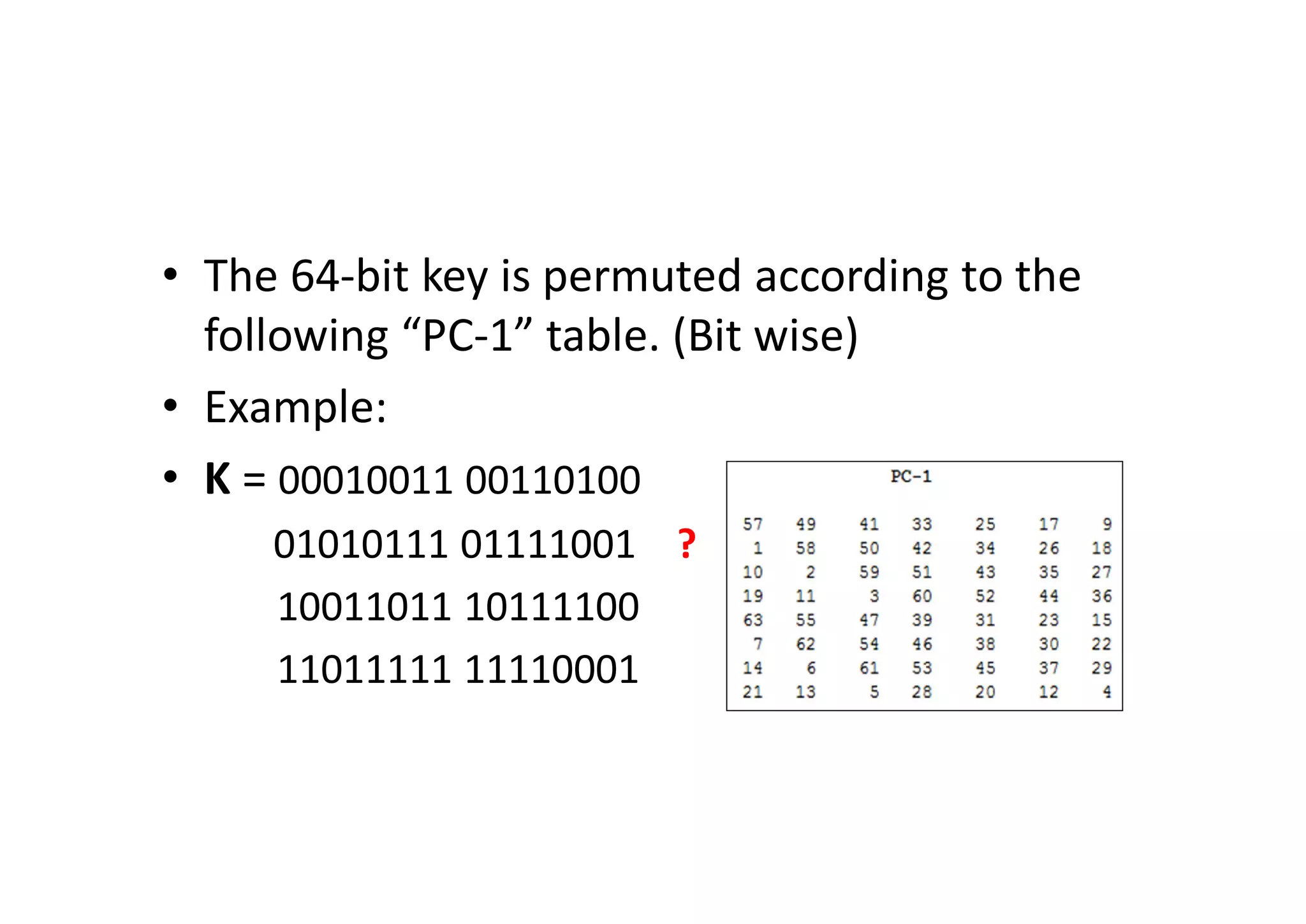
This document discusses block ciphers and the Data Encryption Standard (DES) algorithm. It begins with an overview of stream ciphers and block ciphers, then describes the components of modern block ciphers including substitution boxes (S-boxes), permutation boxes (P-boxes), and operations like XOR. It then explains DES in detail, including the initial permutation, 16 rounds of encryption using 48-bit round keys, and the final permutation. DES encrypts 64-bit blocks using a 56-bit key. The document also covers key generation for DES and the steps to encrypt a plaintext block.

1. Data and Network Security:
Block Ciphers and DES
Adeel Akhtar

2. Agenda
• Stream Cipher & Block Cipher
• Modern Block Cipher
• Block Cipher components
• DES
• 3-DES

3. Stream Cipher & Block Cipher
• A stream cipher is one that encrypts a digital
data stream one bit or one byte at a time.
• A block cipher is an encryption/decryption
scheme in which a block of plaintext is treated
as a whole and used to produce a ciphertext
block of equal length.
– Modern algorithms are based on “block cipher”

4. Modern Block Cipher
• A symmetric-key modern block cipher
encrypts an n-bit block of plaintext or decrypts
an n-bit block of ciphertext.
– The encryption or decryption algorithm uses a k-
bit key

5. Modern Block Cipher (2)
• If the message has fewer than n bits, padding
must be added to make it an n-bit block
• if the message has more than n bits, it should
be divided into n-bit blocks
– appropriate padding must be added to the last
block, if necessary.
– The common values for n are 64, 128, 256, and
512 bits

6. Components of Modern Block Cipher
• Transposition units (P-Boxes)
• Substitution units (S-Boxes)
• exclusive-or operations
• shifting elements
• swapping elements
• splitting elements
• combining elements

7. Components of Modern Block Cipher (2)

8. Permutation Box (P-Box)
• A P-box (permutation box) parallels the
traditional transposition cipher for characters,
but it transposes bits
• Three types of P-boxes in modern block
ciphers
– Straight P-boxes
– Expansion P-boxes
– Compression P-boxes

9. Substitution box (S-Box)
• An S-box can be thought of as a miniature
substitution cipher, but it substitutes bits.
• Unlike traditional substitution cipher, an S-box
can have a different number of inputs and
outputs.
• Exclusive-OR (XOR) function
– the output is 0 if the two inputs are the same
– the output is 1 if the two inputs are different

10. Other Functions
• circular shift operation
– Shifting can be to the left or to the right
– The circular left-shift operation shifts each bit in
an n-bit word k positions to the left
• the leftmost k bits are removed from the left and
become the rightmost bits
• swap operation
– special case of the circular shift operation where
the number of shifted bits k = n/2

11. • Split Operation
– The split operation splits an n-bit word in the
middle, creating two equal-length words
• Combine Operation
– The combine operation normally concatenates
two equal-length words to create an n-bit word.

12. Data Encryption Standard (DES)
• Adopted in 1977 by the National Bureau of
Standards
– data are encrypted in 64-bit blocks using a 56-bit
key
– The algorithm transforms 64-bit input in a series
of steps into a 64-bit output
• The same steps, with the same key, are used
to reverse the encryption

13. DES (Con’t)
• Processing of the plaintext proceeds in three phases.
– 64-bit plaintext passes through an initial permutation (IP)
that rearranges the bits to produce the permuted input
– sixteen rounds of the same function which involves both
permutation and substitution functions.
• output of last round consists of 64 bits that is a function of the
input plaintext and the key
• Left and right halves of the output are swapped to produce the
preoutput
– Finally, the preoutput is passed through a permutation
that is the inverse of the initial permutation function, to
produce the 64-bit ciphertext.

14. DES – General Description

15. INITIAL PERMUTATION (IP) and IP-1
• IP takes a 64-bit input and permutes them
according to a predefined rule.
– IP and its inverse are defined by tables
– Each entry in the permutation table indicates the
position of a numbered input bit in the output, which
also consists of 64 bits
• Final permutation is the inverse of the initial
permutation.
– These two permutations cancel the effect of each
other.
{if the rounds are eliminated from the structures, the ciphertext
is the same as the plaintext.}

16. DES Rounds
• DES uses 16 rounds
• The round takes Li−1 and Ri−1 from the previous round
(or the initial permutation box) and creates Li and Ri,
which go to the next round (or final permutation box).
• Each round can have up to two invertible cipher
elements
– The Swapper swaps the left half of the text with the right
half.
– The mixer is invertible because of the XOR operation. All
noninvertible elements are collected inside the function
f(Ri−1, Ki).

17. DES Function
• Applies a 48-bit key to the rightmost 32 bits
(Ri−1) to produce a 32-bit output
• This function is made up of four sections:
– an expansion P-box
– an exclusive-OR component (that adds key)
– a group of S-boxes
– a straight P-box

18. DES Function (Cont)
• Since Ri−1 is a 32-bit input and Ki is a 48-bit key, we first
need to expand Ri−1 to 48 bits. This expansion
permutation follows a predetermined rule.
• After the expansion permutation, DES uses the XOR
operation on the expanded right section and the round
key. The S-boxes do the real mixing.
– DES uses 8 S-boxes
– each with a 6-bit input and a 4-bit output.
• The last operation in the DES function is a straight
permutation with a 32-bit input and a 32-bit output.

19. Key Generation
• Round-key generator creates sixteen 48-bit
keys out of a 56-bit cipher key
– the cipher key is normally given as a 64-bit key in
which 8 extra bits are the parity bits, which are
dropped before the actual key-generation process

20. DES: Step 1-Key Generation
• Key could be of 8 characters. i.e., BSCS2012 or MS CS012
– These characters will be converted in binary w.r.t.
their respective ASCII codes
– Can you explain other possible options?
• Let K be the hexadecimal key
K = 133457799BBCDFF1

21. • The 64-bit key is permuted according to the
following “PC-1” table. (Bit wise)
• Example:
• K = 00010011 00110100
01010111 01111001 ?
10011011 10111100
11011111 11110001

22. Step 1 (cont.)
• Example: From the original 64-bit key
• K = 00010011 00110100 01010111 01111001
10011011 10111100 11011111 11110001
• we get the 56-bit permutation
K+ = 1111000 0110011 0010101 0101111
0101010 1011001 1001111 0001111

23. Step 1 (cont.)
• Next, split this key into left and right halves, C0
and D0, where each half has 28 bits.
• Example: From the permuted key K+, we get
C0 = 1111000 0110011 0010101 0101111
D0 = 0101010 1011001 1001111 0001111
• With C0 and D0, we now create sixteen blocks
Cn and Dn, 1<=n<=16

24. Step 1 (Cont.)
• Each pair of blocks Cn and Dn is formed from
the previous pair Cn-1 and Dn-1
• “Left shift” will be applied on previous block
according to the given schedule

25. • C0 = 1111000011001100101010101111
D0 = 0101010101100110011110001111
• C1 = 1110000110011001010101011111
D1 = 1010101011001100111100011110
• C2 = 1100001100110010101010111111
D2 = 0101010110011001111000111101
• C3 = 0000110011001010101011111111
D3 = 0101011001100111100011110101
• C4 = 0011001100101010101111111100
D4 = 0101100110011110001111010101
• C5 = 1100110010101010111111110000
D5 = 0110011001111000111101010101
• C6 = 0011001010101011111111000011
D6 = 1001100111100011110101010101
• C7 = 1100101010101111111100001100
D7 = 0110011110001111010101010110
• C8 = 0010101010111111110000110011
D8 = 1001111000111101010101011001
• C9 = 0101010101111111100001100110
D9 = 0011110001111010101010110011
• C10 = 0101010111111110000110011001
D10 = 1111000111101010101011001100
• C11 = 0101011111111000011001100101
D11 = 1100011110101010101100110011
• C12 = 0101111111100001100110010101
D12 = 0001111010101010110011001111
• C13 = 0111111110000110011001010101
D13 = 0111101010101011001100111100
• C14 = 1111111000011001100101010101
D14 = 1110101010101100110011110001
• C15 = 1111100001100110010101010111
D15 = 1010101010110011001111000111
• C16 = 1111000011001100101010101111
D16 = 0101010101100110011110001111

26. Step 1 (Cont.)
• We now form the keys Kn, for 1<=n<=16, by
applying the following permutation table (PC-2)
to each of the concatenated pairs CnDn.
– Each pair has 56 bits, but PC-2 only uses 48 of
these.
• i.e.,14th bit of input will be the first bit of
output

27. • For the first key we have:
C1D1 = 1110000 1100110 0101010 1011111
1010101 0110011 0011110 0011110
• After applying the permutation PC-2, it
becomes
• K1 = 000110 110000 001011 101111 111111
000111 000001 110010

28. Step 1 (Cont.)
• Another example:
– C9D9 will make the key for which round? K?
• Similarly, 16 keys will be formulated
– One for each round
– i.e., K1, K2, K3, K4 . . . . K16
END OF STEP 1

29. Step 2: Encode each 64-bit block of data
• Any message of 8 characters i.e, M HANEEF
– Transformed into bits w.r.t ASCII codes
– Other possible options?
• Lets assume the “hexadecimal” plain text
M=0123456789ABCDEF

30. Step 2 (cont.)
• Starts from an initial permutation IP of the 64
bits of the message data M
– rearranges the bits according to the following
table

31. • Example: Applying the initial permutation to
the block of text M, given previously, we get
• M = 0000 0001 0010 0011 0100 0101 0110
0111 1000 1001 1010 1011 1100 1101 1110
1111
IP = 1100 1100 0000 0000 1100 1100 1111
1111 1111 0000 1010 1010 1111 0000 1010
1010

32. Step 2 (cont.)
• Next divide the permuted block IP into a left
half L0 of 32 bits, and a right half R0 of 32 bits.
• Example: From IP, we get L0 and R0
L0 = 1100 1100 0000 0000 1100 1100 1111 1111
R0 = 1111 0000 1010 1010 1111 0000 1010 1010
• Perform 16 iterations, for 1<=n<=16, using a
function f which operates on two blocks
– a data block of 32 bits
– a key Kn of 48 bits

33. Step 2 (cont.)
• Let + denote XOR addition, then
• Ln = Rn-1
Rn = Ln-1 + f(Rn-1,Kn)
• take right 32 bits of the previous result and
make them the left 32 bits of the current step
• For the right 32 bits in the current step, we
XOR the left 32 bits of the previous step with
the calculation f

34. • Example: For n = 1, we have
• K1 = 000110 110000 001011 101111 111111
000111 000001 110010
L1 = R0 = 1111 0000 1010 1010 1111 0000
1010 1010
R1 = L0 + f(R0,K1)

35. • f(R0,K1)
• R0 contains 32 bit and K1 contains 48 bits
– How to perform XOR operation?
• Answer: Expansion table (E)

36. • Example: We calculate E(R0) from R0 as
follows:
R0 = 1111 0000 1010 1010 1111 0000 1010 1010
E(R0) = 011110 100001 010101 010101 011110
100001 010101 010101
• (Note that each block of 4 original bits has
been expanded to a block of 6 output bits.)

37. Step 2 (cont.)
• Next in the f calculation, we XOR the output E(Rn-1)
with the key Kn:
Kn + E(Rn-1)
• Example: For K1 , E(R0), we have
K1 = 000110 110000 001011 101111 111111
000111 000001 110010
E(R0) = 011110 100001 010101 010101 011110
100001 010101 010101
K1+E(R0) = 011000 010001 011110 111010 100001
100110 010100 100111.

38. • We now have 48 bits but we need to reverse it
in 32 bits. How can we do this?
• Solution: S-boxes
– Each group of six bits will give us an address in a
different S box
– Six bits group will be converted into four bits block

39. Step 2 (cont.) – [S-Boxes]

40. • Practice
• For input block B = 011011 the first bit is "0" and
the last bit "1" giving 01 as the row.
– This is row 1.
• The middle four bits are "1101". This is the binary
equivalent of decimal 13,
– so the column is column number 13.
• In row 1, column 13 appears 5. This determines
the output;
– 5 is binary 0101, so that the output is 0101.
– Hence S1(011011) = 0101

41. • Example: For the first round, we obtain as the
output of the eight S boxes:
• K1 + E(R0) = 011000 010001 011110 111010
100001 100110 010100 100111.
• S1(B1)S2(B2)S3(B3)S4(B4)S5(B5)S6(B6)S7(B7)S8(B8)
= 0101 1100 1000 0010 1011 0101 1001 0111

42. Step 2 (cont.)
• The final stage in the calculation of f is to do a
permutation P of the S-box output to obtain
the final value of f:
• f = P(S1(B1)S2(B2)...S8(B8))
– Permutation of bits
– Permutation table (P) is as under

43. • Example: From the output of the eight S
boxes:
• S1(B1)S2(B2)S3(B3)S4(B4)S5(B5)S6(B6)S7(B7)S8(B8)
= 0101 1100 1000 0010 1011 0101 1001 0111
we get
• f = 0010 0011 0100 1010 1010 1001 1011
1011

44. Step 2 (cont.)
• Now
• R1 = L0 + f(R0 , K1 )
= 1100 1100 0000 0000 1100 1100 1111 1111
+ 0010 0011 0100 1010 1010 1001 1011 1011
= 1110 1111 0100 1010 0110 0101 0100 0100

45. Step 2 (cont.)
• In the next round, we will have L2 = R1, which
is the block we just calculated, and then we
must calculate R2 =L1 + f(R1, K2), and so on for
16 rounds.
• At the end of the sixteenth round we have the
blocks L16 and R16. We then reverse the order
of the two blocks into the 64-bit block
R16L16

46. • Now, apply a final permutation IP-1 as defined
by the following table:

47. • Example: If we process all 16 blocks using the method
defined previously, we get, on the 16th round,
• L16 = 0100 0011 0100 0010 0011 0010 0011 0100
R16 = 0000 1010 0100 1100 1101 1001 1001 0101
• We reverse the order of these two blocks and apply the
final permutation to
• R16L16 = 00001010 01001100 11011001 10010101
01000011 01000010 00110010 00110100
• IP-1 = 10000101 11101000 00010011 01010100
00001111 00001010 10110100 00000101

48. IP-1 = 10000101 11101000 00010011 01010100
00001111 00001010 10110100 00000101
• which in hexadecimal format is
85E813540F0AB405
• Thus the encrypted form of plaintext
M = 0123456789ABCDEF is
C = 85E813540F0AB405
END OF STEP 2

49. Strengths & Weaknesses of DES
• Avalanche Effect
– a change in one bit of the plaintext or one bit of the key produce
a change in many bits of the ciphertext
• Complex to decode for intruders
– 256 key combinations : Hard to launch brute force
• Timing Attack
– information about the key or the plaintext is obtained by
observing how long it takes a given implementation to perform
decryptions on various ciphertexts
• In July 1998, the Electronic Frontier Foundation (EFF) had
broken a DES encryption using a special-purpose “DES
cracker”.
– The attack took less than three days.

50. The 3-Data Encryption Standard
• "The only solution here is to pick an algorithm
with a longer key; there isn't enough silicon in
the galaxy or enough time before the sun
burns out to brute- force triple-DES"
(cryptography expert- Bruce Schneier)

51. The 3-Data Encryption Standard (2)
• Triple-DES is just DES with two 56-bit keys
– the first key is used to encrypt the message
– second key is used to decrypt the encrypted
message
• this decryption just scrambles the data further.
– The twice-scrambled message is then encrypted
again with the first key to yield the final ciphertext
• Triple-DES can also be done with three
separate keys

52. Feistel cipher
• Same as DES
– Eliminate first phase (IP) and third phase (IP-1)
from DES
That’s it: Feistel cipher