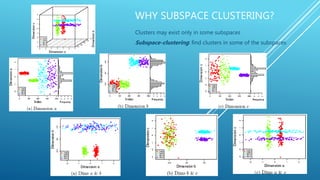
This document discusses the challenges of clustering high-dimensional data due to the curse of dimensionality, leading to the exploration of subspace clustering methods that identify clusters in specific dimensions. Two notable algorithms are presented: Clique, which utilizes density and grid-based approaches to partition data into dense units, and Proclus, which defines clusters and performs a systematic process for medoid selection and outlier detection. The overall goal is to enhance clustering effectiveness by focusing on relevant subspaces rather than relying on a uniform distance measure across all dimensions.

1. COMPARATIVE STUDY OF
SUBSPACE CLUSTERING
ALGORITHMS
NABIL ALSAADI
WASEEM HIJAZI

2. THE CURSE OF
DIMENSIONALITY
 Data in only one dimension is relatively packed
 Adding a dimension “stretches” the points
across that dimension, making them further
apart
 Adding more dimensions will make the points
further apart—high dimensional data is
extremely sparse
 Distance measure becomes meaningless

3. WHY SUBSPACE CLUSTERING?
Clusters may exist only in some subspaces
Subspace-clustering: find clusters in some of the subspaces

4. WHY SUBSPACE CLUSTERING?
 When the number of dimensions increases,
 the distance between any two points is nearly the same
This is the reason why we need to study subspace clustering
 Most known clustering algorithms cluster the data base on the
distance of the data.
 Problem: the data may be near in a few dimensions, but not all
dimensions.
 Such information will be failed to be achieved.

5. SUBSPACE CLUSTERING METHODS
 Subspace search methods: Search various subspaces to
find clusters
 Bottom-up approaches (clique)
 Top-down approaches (proclus)

6. CLIQUE (CLUSTERING IN QUEST)
 Automatically identifying subspaces of a high dimensional data
space that allow better clustering than original space
 CLIQUE can be considered as both density-based and grid-based
 It partitions each dimension into the same number of equal length
interval
 It partitions an m-dimensional data space into non-overlapping
rectangular units
 A unit is dense if the fraction of total data points contained in the unit
exceeds an input threshold τ
 A cluster is a maximal set of connected dense units within a subspace

7. Salary
(10,000)
20 30 40 50 60
age
54312670
20 30 40 50 60
age
54312670
Vacation
(week)
age
Vacation
30 50
 = 3

8. PROCLUS
 Defines an algorithm to find out the clusters and the dimensions for
the corresponding clusters
 Also it is needed to split out those Outliers (points that do not
cluster well) from the clusters.

9. INPUT AND OUTPUT FOR
PROCLUS
 Input:
 The set of data points
 Number of clusters, denoted by k
 Average number of dimensions for each clusters, denoted by L
 Output:
 The clusters found, and the dimensions respected to such clusters

10. PROCLUS
 Three Phase for PROCLUS:
 Initialization Phase
 Iterative Phase
 Refinement Phase

11. INITIALIZATION PHASE
 Choose a sample set of data point randomly.
 Choose a set of data point which is probably the medoids of the
clusters

12. MEDOIDS
 Medoid for a cluster is the data point which is nearest to the center
of the cluster

13. INITIALIZATION PHASE
All Data Points
Random Data Sample
Choose by Random
Size: A × k
The medoids found
Choose in Iterative Phase
Size: k
the set of points including Medoids
Choose by Greedy Algorithm
Size: B × k Denoted by M

14. GREEDY ALGORITHM
 Avoid to choose the medoids from the same clusters.
 Therefore the way is to choose the set of points which are most far
apart.
 Start on a random point

15. ITERATIVE PHASE
 From the Initialization Phase, we got a set of data points which should
contains the medoids. (Denoted by M)
 This phase, we will find the best medoids from M.
 Randomly find the set of points Mcurrent, and replace the “bad” medoids from
other point in M if necessary.
 For the medoids, following will be done:
 Find Dimensions related to the medoids
 Assign Data Points to the medoids
 Evaluate the Clusters formed
 Find the bad medoid, and try the result of replacing bad medoid
 The above procedure is repeated until we got a satisfied result

16. REFINEMENT PHASE-
HANDLE OUTLIERS
 For each medoid mi with the dimension Di, find the smallest
Manhattan segmental distance i to any of the other medoids with
respect to the set of dimensions Di
 jiDiji mmd i
,min 
 i is the sphere of influence of the medoid mi
 A data point is an outlier if it is not under any spheres of influence.

17. THE END