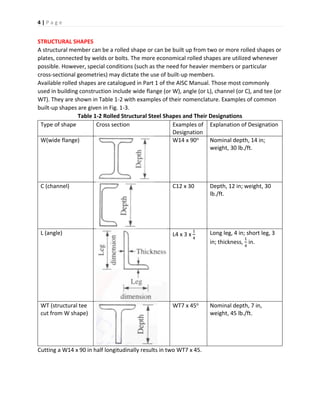
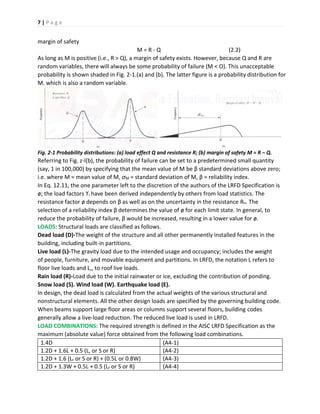
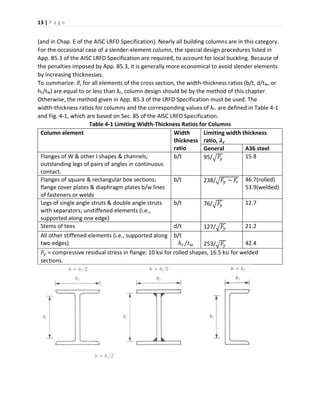
This document provides an overview of steel structures and structural steel design methods. It begins with definitions of common structural steel elements like beams, columns, and connections. It then discusses the mechanical properties and stress-strain behavior of structural steels. Different grades of steel are described along with typical structural shapes. The document concludes with an explanation of the two primary structural steel design methods: Allowable Stress Design (ASD) and Load and Resistance Factor Design (LRFD).

1. 1 | P a g e
Steel Structures - CE329
Written & Composed BY ENGINEER SAQIB IMRAN
Cell no: 0341-7549889
Email: saqibimran43@gmail.com
Student of B.TECH(Civil) at Sarhad University of Science &
Information Technology Peshawer.

2. 2 | P a g e
NOTATION
E = modulus of elasticity of steel = 29,000 kips per square inch (ksi)
Fu = tensile strength, ksi
Fy = yield stress, yield point, or yield strength, ksi
DEFINITIONS
Structural steel, as defined by AISC (in the LRFD Specification and elsewhere), refers to the
steel elements of a structural frame supporting the design loads. It includes steel beams,
columns, beam-columns, hangers, and connections.
Beam-A structural member whose primary function is to carry loads transverse to its
longitudinal axis. Beams are usually horizontal and support the floors in buildings.
Column-A structural member whose primary function is to carry loads in compression along its
longitudinal axis. In building frames, the columns are generally the vertical members which
support the beams.
Beam-column-A structural member whose function is to carry loads both transverse and parallel
to its longitudinal axis. A building column subjected to horizontal forces (such as wind)
is actually a beam-column.
Hanger-A structural member carrying loads in tension along its longitudinal axis.
Connection-The material used to join two or more structural members. Examples of connections
are beam-to-beam and beam-to-column.
MECHANICAL PROPERTIES
The major advantage of steel is its high strength relative to the strengths of the other common
structural materials: wood, masonry, and concrete. Unlike masonry and concrete, which are
weak in tension, steel is strong in both tension and compression. Because of its high strength,
structural steel is widely used in construction. The tallest and longest-span structures are
predominantly steel.
Typical stress-strain curves for structural steel are shown in Fig. 1-2. They are based on the
application of tensile forces to a test specimen. The ordinates (i.e., vertical axes) indicate stress,
which is defined as load divided by cross-sectional area. Units for stress are kips (or kilo pounds;
i.e.,1000 lb) per square inch, commonly noted as ksi. The abscissas (i.e., horizontal axes) indicate
strain, which is a measure of elongation under tension and is defined as the increase in length
divided by the original length. Units for strain are inches per inch; strain is dimensionless.
The stress-strain curve in Fig. 1-2(c) is that of A36 steel, the most commonly used structural
steel. Note the linear relationship between stress and strain in the "elastic range," that is, until
the yield point is reached. The most important design properties of A36 steel [see Fig. 1-2(a)] are
Fy the yield point, the stress at which the proportionality between stress and strain ceases. A36
steel has both an upper and a lower yield point. For design purposes, the yield point of A36 steel
is taken as Fy = 36 ksi, the minimum lower yield point.
Fu, the tensile strength, the maximum stress that the material is capable of sustaining. For 4.36
steel, Fu = 58 to 80 ksi.
E, the modulus of elasticity, which is the (constant) ratio of stress to strain in the elastic ranqe.
For A36 steel, E = 29,000 ksi.

3. 3 | P a g e
The stress-strain curve in Fig. I-2(b) is characteristic of several of the higher-strength steels. All
structural steels have the same modulus of elasticity (E = 29,000 ksi). Unlike A36 steel,
however, the higher-strength steels do not have a definite yield point. For these steels, Fy is the
yield strength as determined by either of the two methods shown in Fig. l-z(b): the 0.2 percent
offset value or the 0.5 percent strain value.
In the AISC Specifications and Manuals, Fy is called the yield stress and, depending on the grade
of steel, can be either the yield point or the yield strength, as defined above.
Fig. 1-2 Stress-strain curves for structural steels: (a) A36 steel; (b) High-strength steel
AVAILABILITY
Fourteen types of structural steel have been approved by the AISC LRFD Specification for use in
buildings. In the LRFD Specification, Sec. A3.1, they are listed by their ASTM (American
Society foi Testing and Materials) specification numbers. The yield stress of these steels ranges
from 36 ksi for the common A36 steel to 100 ksi for A514 steel. As can be seen from Table 1-1
(adapted from Part 1 of the AISC LRFD Manual), the yield stress of a given grade of steel is not a
constant. It varies with plate thickness; very thick structural shapes and plates have reduced
yield stresses. A36 steel is by far the most commonly used type of structural steel for two
reasons: (1): In many applications, the loads and stresses are moderate. Little, if any, saving
would result from the use of higher-strength steels. (2): Even where stress considerations
would favor the use of lighter (possibly more economical) high-strength members, other
criteria may govern. Heavier members may be required to provide increased stiffness to
prevent overall or local instability or excessive deflection. Because stiffness is a function of the
geometric properties of the member and is not affected by strength, no advantage would be
gained from using high-strength steel in such cases.
Steel Type ASTM
Designation
Fy, ksi Plate Thickness, in
Carbon A36
A529
36, 32
42
≤8, >8
≤
1
2
High strength low alloy A441 50, 46, 42, 40
A572-Grade 65
- Grade 60, 50, 42
≤ 1
1
2
,
3
4
-1
1
2
, 1
1
2
− 4, 4-8, ≤
1
1
4
, ≤ 1
1
4
, ≤ 4, ≤ 6
Corrosion resistant High
strength low alloy
A242
A588
50, 46, 42
50, 46, 42
≤
3
4
,
3
4
-1
1
2
, 1
1
2
− 4
≤ 4, 4-5, 5-8
Quenched & tempered
alloy
A514 100, 90 ≤ 2
1
2
, 2
1
2
- 6

4. 4 | P a g e
STRUCTURAL SHAPES
A structural member can be a rolled shape or can be built up from two or more rolled shapes or
plates, connected by welds or bolts. The more economical rolled shapes are utilized whenever
possible. However, special conditions (such as the need for heavier members or particular
cross-sectional geometries) may dictate the use of built-up members.
Available rolled shapes are catalogued in Part 1 of the AISC Manual. Those most commonly
used in building construction include wide flange (or W), angle (or L), channel (or C), and tee (or
WT). They are shown in Table 1-2 with examples of their nomenclature. Examples of common
built-up shapes are given in Fig. 1-3.
Table 1-2 Rolled Structural Steel Shapes and Their Designations
Type of shape Cross section Examples of
Designation
Explanation of Designation
W(wide flange) W14 x 90o Nominal depth, 14 in;
weight, 30 lb./ft.
C (channel) C12 x 30 Depth, 12 in; weight, 30
lb./ft.
L (angle) L4 x 3 x
1
4
Long leg, 4 in; short leg, 3
in; thickness,
1
4
in.
WT (structural tee
cut from W shape)
WT7 x 45o Nominal depth, 7 in,
weight, 45 lb./ft.
Cutting a W14 x 90 in half longitudinally results in two WT7 x 45.

5. 5 | P a g e
Fig. 1-3 Common built-up structural shapes
DESIGN METHODS
Two methods for selecting structural steel members are recognized in current engineering
practice in the United States. The allowable stress design (ASD) method has been codified by
AISC, from 1923 to the present, in nine successive editions of their Specification for the Design,
Fabrication and Erection of Structural Steel for Buildings (also known as the AISC Specification).
This document has been incorporated by reference in virtually every building code in the United
States. Containing the AISC Specification as well as numerous design aids for the ASD method
has been the AISC Manual of Steel Construction (also known as the ,41SC Manual). The new
load and resistance factor design (LRFD) method was introduced officially by AISC in 1986 with
their publication of the Load and Resistance Factor Design Specification for Structural Steel
Buildings (also known as the AISC LRFD Specification) and the Load and Resistance Factor
Design Manual of Steel Construction (also known as the AISC LFRD Manual). The LFRD Manual
contains the LFRD Specification and many tables and charts to assist users of the LRFD method.
This book, devoted exclusively to the LFRD method of structural steel design, is based on the
AISC LFRD Specification. At the date of publication of this text, almost all U.S. jurisdictions have
approved the use of the AISC LFRD Specification. It is anticipated that LFRD will soon be
universally accepted in the country and will eventually become the standard method of
structural steel design.
ASD Vs LRFD Methods
(This section, which compares the two methods of structural steel design, is not essential for an
understanding of the LFRD method or the remainder of this book. Hence, it may be skipped by
students and others. It should, however, be of interest to those readers who have used ASD or
are otherwise familiar with it.)
The ASD method is characterized by the use of one judgmental factor of safety. A limiting stress
(usually Fy) is divided by a factor of safety (FS, determined by the authors of the specification)
to arrive at an allowable stress.
Allowable stress =
Fy
FS

6. 6 | P a g e
Actual stresses in a steel member are calculated by dividing forces or moments by the
appropriate section property (e.g. area or section modulus). The actual stresses are then
compared with the allowable stresses to ascertain that,
Actual stress ≤ allowable stress
No distinction is made among the various kinds of loads. Because of the greater variability and
uncertainty of the live load and other loads in comparison with the dead load, a uniform
reliability for all structures is not possible. LFRD uses a different factor for each type of load and
another factor for the strength or resistance. Each factor is the result of a statistical study of the
variability of the subject quantity. Because the different factors reflect the degrees of
uncertainty in the various loads and the resistance, a uniform reliability is possible.
INTRODUCTION TO LRFD
NOTATION: D = dead load, E = earthquake load, L = live load, L = roof live load, M = margin of
safety, Q = load, R = rain load, R = resistance, Rn = nominal resistance, S = snow load, W = wind
load, β = reliability index, ϒ = load factor, ø = resistance factor, ơ = standard deviation.
BASIC CONCEPTS: Load and resistance factor design (LRFD) is a method for designing structures
so that no applicable limit state is exceeded when the structure is subjected to all appropriate
combinations of factored loads. Limit state is a condition in which a structure or a structural
component becomes unfit. A structural member can have several limit states. Strength limit
states concern safety and relate to maximum load-carrying capacity (e.g., plastic hinge and
buckling). Serviceability limit states relate to performance under normal service conditions (e.g.,
excessive deformation and vibration).
The LRFD method, as applied to each limit state, may be summarized by the formula
∑ γiQi ≤ ∅Rn (2.1)
In the terminology of the AISC LRFD Specification, the left side of the inequality is the required
strength and the right side is the design strength. The left side represents the load combinations;
that is, the summation (denoted by Ʃ) of the various loads (or load effects) Qi, multiplied by their
respective load factors ϒi. The left side is material-independent; the loads are taken from the
governing building code and the LRFD load factors were derived from statistical building load
studies. Loads and load combinations are covered later in this chapter. On the right side of the
inequality, the design strength for the given limit state is the product of the nominal strength or
resistance Rn and its resistance factor ø. Succeeding chapters of this text cover the limit states
applicable to columns, beams, and other structural elements, together with the corresponding
resistances and resistance factors.
Associated with each limit state are values for Rn and ø where Rn defines the boundary of
structural usefulness; ø (always less than or equal to one) depends on the variability of Rn. Test
data were analyzed to determine the uncertainty in each resistance. The greater the scatter in
the test data for a given resistance, the lower its ø factor.
PROBABILITY THEORY: The following is a brief, simplified explanation of the basis of LRFD in
probability theory. The load effect Q and the resistance R are assumed to be statistically
independent random variables with probability distributions as shown in Fig. 2-1.(a). Let the

7. 7 | P a g e
margin of safety
M = R - Q (2.2)
As long as M is positive (i.e., R > Q), a margin of safety exists. However, because Q and R are
random variables, there will always be some probability of failure (M < O). This unacceptable
probability is shown shaded in Fig. 2-1.(a) and (b). The latter figure is a probability distribution for
M. which is also a random variable.
Fig. 2-1 Probability distributions: (a) load effect Q and resistance R; (b) margin of safety M = R – Q.
Referring to Fig. z-l(b), the probability of failure can be set to a predetermined small quantity
(say, 1 in 100,000) by specifying that the mean value of M be β standard deviations above zero;
i.e. where M = mean value of M, ơM = standard deviation of M, β = reliability index.
In Eq. 12.11, the one parameter left to the discretion of the authors of the LRFD Specification is
ø; the load factors ϒi have been derived independently by others from load statistics. The
resistance factor ø depends on β as well as on the uncertainty in the resistance Rn. The
selection of a reliability index β determines the value of ø for each limit state. In general, to
reduce the probability of failure, β would be increased, resulting in a lower value for ø.
LOADS: Structural loads are classified as follows.
Dead load (D)-The weight of the structure and all other permanently installed features in the
building, including built-in partitions.
Live load (L)-The gravity load due to the intended usage and occupancy; includes the weight
of people, furniture, and movable equipment and partitions. In LRFD, the notation L refers to
floor live loads and L,, to roof live loads.
Rain load (R)-Load due to the initial rainwater or ice, excluding the contribution of ponding.
Snow load (S). Wind load (W). Earthquake load (E).
In design, the dead load is calculated from the actual weights of the various structural and
nonstructural elements. All the other design loads are specified by the governing building code.
When beams support large floor areas or columns support several floors, building codes
generally allow a live-load reduction. The reduced live load is used in LRFD.
LOAD COMBINATIONS: The required strength is defined in the AISC LRFD Specification as the
maximum (absolute value) force obtained from the following load combinations.
1.4D (A4-1)
1.2D + 1.6L + 0.5 (L, or S or R) (A4-2)
1.2D + 1.6 (Lr or S or R) + (0.5L or 0.8W) (A4-3)
1.2D + 1.3W + 0.5L + 0.5 (Lr or S or R) (A4-4)

8. 8 | P a g e
1.2D + 1.5E + (0.5L or 0.2S) (A4-5)
0.9D – (1.3W or 1.5E) (A4-6)
[Exception: The load factor on L in combinations (A4-3), (A4-4), and (A4-5) shall equal 1.0 for
garages, areas occupied as places of public assembly, and all areas where the live load is greater
than 100 lb/ft2.]
Loads D, L, L,, S, R, W, and E represent either the loads themselves or the load effects (i.e.,
the forces or moments caused by the loads). In the preceding expressions, only one load
assumes its maximum lifetime value at a time, while the others are at their "arbitrary point-in-
time" values. Each combination models the design loadings condition when a different load is at
its maximum.
Load Combination Load at Its Lifetime Maximum
(A4-1) D (during construction; other loads not present)
(A4-2) L
(A4-3) Lr or S or R (a roof load)
(A4-4) W (acting in the direction of D)
(A4-5) E (acting in the direction of D)
(A4-6) W or E (opposing D)
Load combinations (A4-1) to (A4-6) are for computing strength limit states. In determining
serviceability limit states (e.g., deflections) the un-factored (service) loads are used.
Problems based on the determination of loads
2.1. The moments acting on a floor beam are a dead-load moment of 50 kip-ft and a live-load
moment of 35 kip-ft. Determine the required strength.
Because dead load and floor live load are the only loads acting on the member, Lr = S = R = W =
E = 0. By inspection of formulas (A4-1) to (A4-6), it is obvious that one of the first two formulas
must govern, as follows.
1.4D = 1.4 x 50 kip-ft = 70 kip-ft (A4-1)
1.2D + 1.6L = 1.2 x 50 kip-ft + 1.6 x 35 kip-ft = 116 kip-fl (A4-2)
Because it produces the maximum required strength, the second load combination governs.
The required strength is 116 kip-ft.
2.2. Floor beams W21 x 50, spaced 10 ft 0 in center-to-center, support a superimposed dead
load of 65lb/ft2 and a live load of 40lb/ft2. Determine the governing load combination and the
corresponding factored load.
Total dead load D : 50lb/ft + 65 lb/ft2 x 10.0 ft = 700lb/ft
Total live load L : 40lb/ft2 x 10.0 ft = 400 lb/ft
As in Prob. 2.1, Lr = S = R = W = E = 0.
The two relevant load combinations are
1.4D = 1.4 x 7O0 lb/ft = 980Ib/ft (A4-1)
1.2D + 1.6L = 1.2 x 700lb/ft + 1.6 x 400 lb/ft = 1480 lb/ft (A4-2)
The second load combination, which gives the maximum factored load, 1480lb/ft (or
1.48 kips/ft), governs.

9. 9 | P a g e
2.3. Roof design loads include a dead load of 35lb/ft2, a live (or snow) load of 25lb/ft2, and a
wind pressure of 15lb/ft2 (upward or downward). Determine the governing loading.
The six load combinations are
Load Combination Factored load Lb.ft2.
(A4-1) 1.4 x 35 = 49
(A4-2) 1.2 x 35 + 0 + 0.5 x 25 = 55
(A4-3) 1.2 x 35 + 1.6 x 25 + 0.8 x 15 = 94
(A4-4) 1.2 x 35 + 1.3 x 15 + 0 + 0.5 x 25 = 74
(A4-5) 1.2 x 35 + 0 + 0.2 x 25 = 47
(A4-6) 0.9 x 35 – 1.3 x 15 = 12
The third load combination governs; it has a total factored load of 94lb/ft2.
2.4. The axial forces on a building column from the code-specified loads have been calculated
as 200 kips of dead load, 150 kips (reduced) floor live load, 25 kips from the roof (Lr or S or R),
100 kips from wind, and 40 kips from earthquake. Determine the required strength of the
column.
Load Combination Factored Axial force Kips
(A4-1) 1.4 x 200 = 280
(A4-2) 1.2 x 200 + 1.6 x 150 + 0.5 x 25 = 493
(A4-3a) 1.2 x 200 + 1.6 x 25 + 0.5 x 150 = 355
(A4-3b) 1.2 x 200 + 1.6 x 25 + 0.8 x 100 = 360
(A4-4) 1.2 x 200 + 1.3 x 100 + 0.5 x 150 + 0.5 x 25 = 458
(A4-5a) 1.2 x 200 + 1.5 x 40 + 0.5 x 150 = 375
(A4-5b) 1.2 x 200 + 1.5 x 40 + 0.2 x 25 = 305
(A4-6a) 0.9 x 200 – 1.3 x 100 = 50
(A4-6b) 0.9 x 200 – 1.5 x 40 = 120
The required strength for the column is 493 kips, based on the second load combination.
2.5. Repeat Prob. 2.4 for a garage column.
According to the AISC LRFD Specification, load combinations (A4-3) to -(A4-5) are modified for
garages, areas of public assembly, and areas with live load exceeding 100 lb/ft'z. as follows.
1.2D + 1.6 (Lr or S or R) + (1.0L or 0.8W) (A4-3)
1.2D + 1.3W + 1.0L + 0.5 (Lr or S or R) (A4-4)
1.2D + 1.5E + (1.0L or 0.2S) (A4-5)
The solution to Prob. 2.4 is still valid for garages except for load combinations (A4-k3a), (A4-4),
and (A4-5A), which become
Load Combination Factored Axial force Kips
(A4-3a) 1.2 x 200 + 1.6 x 25 + 1.0 x 150
(A4-4) 1.2 x 200 + 1.3 x 100 + 1.0 x 150 + 0.5 x 25
(A4-5a) 1.2 x 200 + 1.5 x 40 + 1.0 x 150
Because 533 kips is greater than 493 kips, the required strength for the garage column is 533
kips, which is obtained from modified load combination (A4-4).
DESIGN OF TENSILE STRENGTH AND DISPLACEMENT

10. 10 | P a g e
DESIGN TENSILE STRENGTH
Two criteria limit the design tensile strength øtPn.
a. For yielding of the gross cross section
øt = 0.90
Pn = FyAg (D1-1)
b. For fracture in the net cross section
øt = 0.75
Pn = FuAe (D1-2)
Where: øt = resistance factor for tension, Pn = nominal axial strength, kips
Fy = specified minimum yield stress, ksi, Fu = specified minimum tensile strength, ksi
Limitation a is intended to prevent excessive elongation of the member. Since the fraction of
the total member length occupied by fastener holes is usually small, the effect of early yielding
of the reduced cross sections on the total elongation of the member is negligible. Hence the
gross section is used. Limit state b deals with fracture at the cross section with the minimum Ae.
DISPLACEMENT
The increase in the length of a member due to axial tension under service loads is
∆ =
Pl
EAg
[3.1]
where: ∆ = axial elongation of the member, in. P = (un-factored) axial tensile force in the
member, kips. l = length of the member, in. E = modulus of elasticity of steel = 29,000 ksi.
PROBLEMS BASED ON THE CROSS-SECTIONAL AREAS OF PLATES
3.1. Determine the gross and net cross-sectional areas of a plate l2inx 2in with a l-in-diameter
hole. (See Fig. 3-2.)
Gross area - gross width x thickness = Ag = 12 in x 2 in = 24 in2.
Net area = net width x thickness, Net width = gross width - hole diameter
For design, hole diameter = 1 in +
1
16
in = 1.06 in
Net width = 12 in - 1.06 in = 10.94 in, An = 10.94 in x 2 in = 21.88 in2.
3.2. Use the same information as in prob 3.1 except with two 1-in diameter holes positioned
as shown in Fig. 3.3.
Gross width of plate = 12 in, Ag = 24 in2. As above.

11. 11 | P a g e
Chain ACE or BDF (one hole): Net width = 12 in – 1.06 in = 10.94 in.
Chain ACDF (two holes, one space): Net width = gross width - ∑ ℎ𝑜𝑙𝑒 diameters + ∑
𝑠3
4𝑔
= 12 in – 2 x 1.06 in +
(4 𝑖𝑛)2
4 𝑋 6 𝑖𝑛
= 10.54 in. Because 10.54 in < 10.94 in, chain ACDF is critical in this
case: An = net width x thickness = 10.54 in x 2 in = 21.08 in2.
Fig. 3.3.
3.3. Use the same information as in prob.3.1, except with three 1-in-diameter holes
positioned as shown in Fig. 3-4.
Ag = 24 in2.
Fig. 3-4.
Regarding net width, by inspection, chains BDG (one hole), ACDG (two holes, one space), &
BDEF (two holes, one space) are not critical. For other chains.
Chain
Net Width (in) = Gross Width - ∑ 𝒉𝒐𝒍𝒆 diameters + ∑
𝒔 𝟑
𝟒𝒈
ACEF 12 – 2 x 1.06 = 1.98
ACDEF
12 – 3 x 1.06 + 2 x
32
4 𝑋 3
Chain ACEF with the minimum net width, 9.88 in, is critical: An = 9.88 x 2 = 19.75 in2.
3.4. Holes have been punched in the flanges of the W10 x 49 in Fig. 3.5 for four 1-in diameter
bolts. The holes lie in the same cross sectional plane; Ag = 14.4 in2. Determine the net area.
For design, hole diameter = 1 in +
1
8
in = 1.13 in. An = As – 4 x hole diameter x flange thickness
= 14.4 in2 – 4 x 1.13 x 0.560 ⇒ An = 11.88 in2.

12. 12 | P a g e
In probs. 3.5 to 3.6, determine the design tensile strength of a W10 x 49 in A36 steel, with the
conditions stated.
3.5. No holes; the two flanges & the web are all welded to the supporting member.
Here, Ae = Ag = 1.4 in2. For A36 steel, Fy = 36 ksi and Fu = 58 ksi.
Design strength øtPn = minimum of: 0.90FyAg = 0.90 x 36 ksi x 14.4 in2 = 467 kips.
0.75 FuAe = 0.75 x 58 ksi x 14.4 in2 = 626 kips. øtPn = 467 kips, based on yielding gross section.
3.6. No holes; only the flanges of the W10 x 49 are welded to the support.
Ag = 14.4 in2. For welded connections, effective net area: Ae = area of directly connected
elements = area of the two flanges = 2(10 in x 0.560 in) = 11.20 in2.
Design strength øtPn = minimum of: 0.90FyAg = 0.90 x 36 ksi x 14.4 in2 = 467 kips.
0.75 FuAe = 0.75 x 58 ksi x 11.20 in2 = 487 kips. øtPn = 467 kips, based on yielding gross section.
3.7. The hole pattern of Fig. 3-5., but not at the end; the flanges of the W10 x 49 are welded to
the support.
Ag = 14.4 in2. At the support Ae = flange area = 11.20 in2, as in prob
3.7. A W10 x 49 tension hanger, 5 ft long, carries a service load of 250 kips. Calculate its axial
elongation.
Sol: Elongation ∆=
𝑃𝑙
𝐸𝐴 𝑔
=
250 𝑘𝑖𝑝𝑠 ×(5.0 𝑓𝑡 ×12𝑖𝑛/𝑓𝑡)
29,000 𝑘𝑠𝑖 ×14.4 𝑖𝑛2
= 0.36 in.
LOCAL BUCKLING
The cross sections of structural steel members are classified as either compact, non-compact,
or slender-element sections, depending on the width-thickness ratios of their elements.
A section is compact if the flanges are continuously connected to the web, and the
width-thickness ratios of all its compression elements are equal to or less than λp.
A section is non-compact if the width-thickness ratio of at least one element is greater than λp,
provided the width-thickness ratios of all compression elements are equal to or less than λr.
If the width-thickness ratio of a compression element is greater than λr, that element is a
slender compression element; the cross section is called a slender-element section.
Steel members with compact sections can develop their full compressive strength without local
instability. Non-compact shapes can be stressed to initial yielding before local buckling occurs.
In members with slender elements, elastic local buckling is the limitation on strength.
Columns with compact and non-compact sections are designed by the method described herein

13. 13 | P a g e
(and in Chap. E of the AISC LRFD Specification). Nearly all building columns are in this category.
For the occasional case of a slender-element column, the special design procedures listed in
App. B5.3 of the AISC LRFD Specification are required, to account for local buckling. Because of
the penalties imposed by App. B5.3, it is generally more economical to avoid slender elements
by increasing thicknesses.
To summarize: if, for all elements of the cross section, the width-thickness ratios (b/t, d/tw, or
hc/tw) are equal to or less than λr, column design should be by the method of this chapter.
Otherwise, the method given in App. B5.3 of the LRFD Specification must be used. The
width-thickness ratios for columns and the corresponding values of λr. are defined in Table 4-1
and Fig. 4-1, which are based on Sec. 85 of the AISC LRFD Specification.
Table 4-1 Limiting Width-Thickness Ratios for Columns
Column element Width
thickness
ratio
Limiting width thickness
ratio, 𝝀 𝒓
General A36 steel
Flanges of W & other I shapes & channels;
outstanding legs of pairs of angles in continuous
contact.
b/t 95/√ 𝐹𝑦 15.8
Flanges of square & rectangular box sections;
flange cover plates & diaphragm plates b/w lines
of fasteners or welds
b/t 238/√ 𝐹𝑦 − 𝐹𝑟 46.7(rolled)
53.9(welded)
Legs of single angle struts & double angle struts
with separators; unstiffened elements (i.e.,
supported along one edge)
b/t 76/√ 𝐹𝑦 12.7
Stems of tees d/t 127/√ 𝐹𝑦 21.2
All other stiffened elements (i.e., supported along
two edges)
b/t
ℎ 𝑐/𝑡 𝑤 253/√ 𝐹𝑦 42.4
𝐹𝑦 = compressive residual stress in flange: 10 ksi for rolled shapes, 16.5 ksi for welded
sections.

14. 14 | P a g e
Fig. 4-1 Definitions of widths (b, d, and hc) and thickness (flange or leg thickness t and web
thickness tw) for use in Table 4-1
COLUMN BUCKLING
The most significant parameter affecting column stability is the slenderness ratio Kl/r, where l(it
is L) is the actual unbraced length of the column, in; Kl is the effective length of the column, in;
and r is the radius of gyration of the column cross section, in. Column strength equations are
normally written for ideal "pin-ended" columns. To make the strength equations applicable to
all columns, an effective length factor K is used to account for the influence of end conditions
on column stability. Two methods for determining K for a column are presented in Sec. C2 of
the Commentary on the AISC LRFD Specification: a judgmental method and an approximate
analytical method. A discussion of the two methods follows.
EFFECTIVE LENGTH FACTOR: JUDGMENTAL METHOD
Six cases are shown in Table 4-2 for individual columns, with their corresponding K values, both
theoretical and recommended. The more conservative recommendations (from the Structural
Stability Research Council) reflect the fact that perfect fixity cannot be achieved in real structures.
The LRFD Specification distinguishes between columns in braced and unbraced frames. In braced
frames, sides way is inhibited by diagonal bracing or shear walls. In Table 4-2, case d (the classical
pin-ended column, K = 1.0) as well as cases a and b represent columns in braced frames; K ≤ 1.0.
AISC recommends that K for compression members in braced frames "shall be taken as unity,
unless structural analysis shows that a smaller value may be used." It is common practice to
assume K = 1.0 for columns in braced frames.
Cases c, e; and f in Table 4-2 cover columns in unbraced frames (sides way uninhibited); K ≥
1.0. The K values recommended there in may be used in column design.
Table 4-2 Effective Length Factors K for Columns

15. 15 | P a g e
Buckled shape of column
shown by dashed line
Theoretical K value 0.5 0.7 1.0 1.0 2.0 2.0
Recommended design
values when ideal
conditions are
approximated
0.65 0.80 1.2 1.0 2.10 2.0
End condition code Rotation fixed and translation fixed
Rotation free and translation fixed
Rotation fixed and translation free
Rotation free and translation free
Reproduced with permission from the AISC LFRD Manual.
EFFECTIVE LENGTH FACTOR: ANALYTICAL METHOD
If beams are rigidly connected to a column, nomographs are available for approximating K for
that column. Two such "alignment charts" have been developed: one for "sides way inhibited"
(i.e., braced frames, K ≤ 1.0); the other, for "sides way uninhibited" (i.e., unbraced frames, K ≥
1.0). Again, for columns in braced frames, it is customary to conservatively let K = 1.0' For
columns in unbraced frames, the alignment chart in Fig. 4-2 may be used to determine K.
Because the alignment charts were developed with the assumption of purely elastic action, the
stiffness reduction factors (SRF) in Table 4-3 are available to account for inelastic column
behavior. (Figure 4-2 has been reproduced with permission from the Commentary on the AISC
LRFD Specification. Table 4-3 is a corrected version of Table A in the AISC LRFD Manual, Part 2.)
The procedure for obtaining K from Fig. 4-2 is as follows.
1. At each of the two joints (A and B) at the ends of the column, determine i(the moment of
inertia, in4) and L (the unbraced length, in) of each column ci and each beam gi rigidly connected
to that joint and lying in the plane in which buckling of the column is being considered.
2. At each end of the column, A and B

16. 16 | P a g e
G’ =
(𝐼/𝑙)𝑐1+ (𝐼/𝑙)𝑐2
(𝐼/𝑙)𝑔1+ (𝐼/𝑙)𝑔2
[4.1]
GA K GB
100.0
50.0
30.0
20.0
10.0
9.0
8.0
7.0
6.0
5.0
4.0
3.0
2.0
1.0
0
20.0
10.0
5.0
4.0
3.0
2.0
1.5
1.0
Sidesway uninhibited
100.0
50.0
30.0
20.0
10.0
9.0
8.0
7.0
6.0
5.0
4.0
3.0
2.0
Fig. 4-2 Alignment chart for effective length of columns I unbraced frames having rigid joints.
Table 4-3. Stiffness Reduction Factors for A36 steel for use with Fig. 4-2.
Pu/Ag, ksi SRF Pu/Ag, ksi SRF
30 0.05 20 0.76
29 0.14 19 0.81
28 0.22 18 0.85
27 0.30 17 0.89
26 0.38 16 0.92
25 0.45 15 0.95
24 0.52 14 0.97
23 0.58 13 0.99
22 0.65 12 1.00
21 0.70
Pu is the required strength and Ag is the gross cross sectional area of the subject column.

17. 17 | P a g e
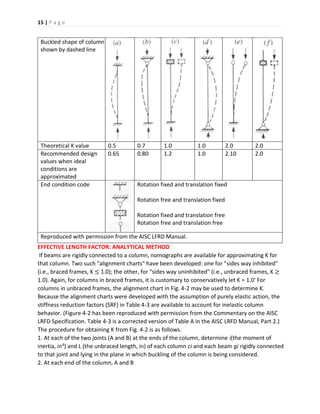
3. Adjust for inelastic column action: GA = G’A x SRF ⇒ GB = G’B x SRF [4.2]
where SRF is the stiffness reduction factor for the column obtained from Table 4-3.
4. For a column end attached to a foundation, G = 10 for a "pin" support and G = 1 for a rigid
support are recommended.
5. Determine K by drawing a straight line from GA to GB on the alignment chart in Fig. 4-2.
DESIGN COMPRESSIVE STRENGTH
Column buckling can be either elastic or inelastic. For design purposes, λc = 1.5 is taken as the
boundary between elastic and inelastic column buckling.
λ 𝑐 =
𝐾𝑙
𝑟𝜋
√
𝐹𝑦
𝐸
(E2-4)
For columns with cross-sectional elements having width-thickness ratios equal to or less than
λr, the design compressive strength is øcPn, where: øc = 0.85
Pn = AgFcr (E2-1)
If λc ≤ 1.5, column buckling is inelastic.
Fcr = (0.658λ 𝑐2
)Fy (E2-2)
Or in the alternate from given in the Commentary on the AISC LFRD Specification
Fcr = [exp(- 0.419λ 𝑐2
)Fy (C-E2-1)
Where exp(x) = ex. If λc ≤ 1.5, column buckling is elastic. Fcr = [
0.877
λ 𝑐2
]Fy (E-2-3)
The terms in these Equations include: λc = slenderness parameter, øc = resistance factor for
compression, Fy = specified minimum yield stress, ksi, Pn = nominal compressive strength, kips,
E = modulus of elasticity of steel = 29,000 ksi. Fcr = critical compressive stress, ksi. Ag = gross
cross-sectional area, in2.
Equation (E2-3) is the Euler equation for column instability multiplied by 0.877 to account for
the initial out-of-straightness of actual columns. Equation (E2-2) & (its equivalent) Eq. (C-E2-1)
are empirical equations for inelastic column buckling, providing a transition from Fcr = Fy at λc =
0 (i.e., Kl/r = 0) to the modified Euler equation [Eq. (E2-3)] for elastic buckling at λc > 1.5. For
A36 steel λc = 1.5 corresponds to a slenderness ratio Kl/r of 133.7.
COLUMN DESIGN
According to Sec. B7 of the AISC LRFD Specification, for compression members KL/r "preferably'
should not exceed 200'". In design, selection of an appropriate column can be facilitated by
referral to tables in one of two ways. The design compressive strengths øcPn of W and other
rolled shapes are tabulated in the AISC LRFD Manual, Part2. Column shapes can be selected
directly from those tables. For built-up sections and rolled shapes not tabulated, Table 4-4 for
A36 steel (and similar tables for other grades of steel in the AISC LFRD Specification) can be
used in iterative design. In both cases, reference to tables replaces the need to solve the
column strength equations [Eqs. (E2-1) ro (E2-4)].
Table 4-4 Design Compressive Stresses for A36 Steel
Design Stress for compression Members of 36 ksi Specified yield-Stress Steel, øc = 0.85*

18. 18 | P a g e
𝑲𝒍
𝒓
øcFcr, ksi
𝑲𝒍
𝒓
øcFcr, ksi
𝑲𝒍
𝒓
øcFcr, ksi
𝑲𝒍
𝒓
øcFcr, ksi
𝑲𝒍
𝒓
øcFcr, ksi
1 30.60 41 28.01 81 21.66 121 14.16 161 8.23
2 30.59 42 27.01 82 21.48 122 13.98 162 8.13
3 30.59 43 27.76 83 21.29 123 13.80 163 8.03
4 30.57 44 27.64 84 21.11 124 13.62 164 7.93
5 30.56 45 27.51 85 21.92 125 13.44 165 7.84
6 30.54 46 27.37 86 20.73 126 13.27 166 7.74
7 30.52 47 27.24 87 20.54 127 13.09 167 7.65
8 30.50 48 27.11 88 20.36 128 12.92 168 7.56
9 30.47 49 26.97 89 20.17 129 12.74 169 7.47
10 30.44 50 26.83 90 19.98 130 12.57 170 7.38
11 30.41 51 26.68 91 19.79 131 12.40 171 7.30
12 30.37 52 26.54 92 19.60 132 12.23 172 7.21
13 30.33 53 26.39 93 19.41 133 12.06 173 7.13
14 30.29 54 26.25 94 19.22 134 11.88 174 7.05
15 30.24 55 26.10 95 19.03 135 11.71 175 6.97
16 30.19 56 25.94 96 18.84 136 11.54 176 6.89
17 30.14 57 25.79 97 18.65 137 11.37 177 6.81
18 30.08 58 25.63 98 18.46 138 11.20 178 6.73
19 30.02 59 25.48 99 18.27 139 11.04 179 6.66
20 29.96 60 25.32 100 18.08 140 10.89 180 6.59
21 29.90 61 25.16 101 17.89 141 10.73 181 6.51
22 29.83 62 24.99 102 17.70 142 10.58 182 6.44
23 29.76 63 24.83 103 17.51 143 10.43 183 6.37
24 29.69 64 24.67 104 17.32 144 10.29 184 6.30
25 29.61 65 24.50 105 17.13 145 10.15 185 6.23
26 29.53 66 24.33 106 16.94 146 10.01 186 6.17
27 29.45 67 24.16 107 16.75 147 9.87 187 6.10
28 29.36 68 23.99 108 16.56 148 9.74 188 6.04
29 29.28 69 23.82 109 16.37 149 9.68 189 5.97
30 29.18 70 23.64 110 16.19 150 9.41 190 5.91
31 29.09 71 23.47 111 16.00 151 9.36 191 5.85
32 28.99 72 23.29 112 15.81 152 9.23 192 5.79
33 28.90 7 23.12 113 15.63 153 9.11 193 5.73
34 28.79 74 22.94 114 15.44 154 9.00 194 5.67
35 28.69 75 22.76 115 15.26 155 8.88 195 5.61
36 28.58 76 22.58 116 15.07 156 8.77 196 5.55
37 28.47 77 22.40 117 14.89 157 8.66 197 5.50
38 28.36 78 22.22 118 14.70 158 8.55 198 5.44
39 28.25 79 22.03 119 14.52 159 8.44 199 5.39
40 28.13 80 21.85 120 14.34 160 8.33 200 5.33

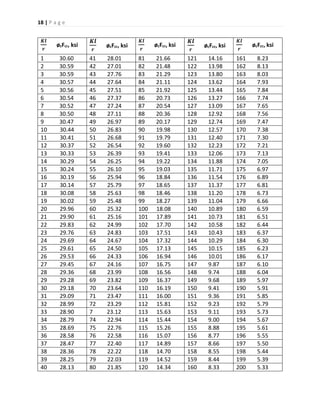
19. 19 | P a g e
When element width-thickness ratio exceeds λr, see App. B5.3. LFRD Specification.
Reproduced with permission from the AISC LFRD Manual.
Building columns are most commonly W shapes, in the W14-W4 series. The W14 and W12
series are well suited to carrying heavy loads in multistory buildings. The W16 to W40 series are
seldom used for columns because of their inefficiency due to their relatively low values of ry
(the radius of gyration about the weak y axis). The most efficient column sections are structural
shapes with rx = ry (i.e., equal radii of gyration about both principal axes). Included in this
category are pipe and tube shapes, which are often used in lightly loaded single-story
applications. Because they are rolled only with relatively small cross sections, structural pipes
and tubes are not available for carrying heavy column loads.
DISPLACEMENT
The decrease in the length of a member due to axial compression under service loads is
∆=
𝑃𝑙
𝐸𝐴 𝑔
[4.3], Where, ∆ = axial shortening of the member, in. P = (un-factored) axial
compressive force in the member, kips. L = length of the member, in.
Solved Examples
In probs. 4.1 to 4.3, determine whether the given column shape is a slender-element section.
(a) In A36 steel (Fy = 36 ksi) (b) If Fy = 50 ksi.
4.1. W14 x 34. If the width-thickness ratio of an element is greater than λr, it is a slender
element. Referring to Table 4-1 and Fig. 4-1, for the flanges of a W shape.
λr =
95
√ 𝐹𝑦
= {
95
√36
= 15.8 𝑖𝑓 𝐹𝑦 = 36 𝑘𝑠𝑖
95
√50
= 13.4 𝑖𝑓 𝐹𝑦 = 50 𝑘𝑠𝑖
for the web of a W shape: λr =
253
√ 𝐹𝑦
= {
253
√36
= 42.2 𝑖𝑓 𝐹𝑦 = 35 𝑘𝑠𝑖
253
√50
= 35.8 𝑖𝑓 𝐹𝑦 = 50 𝑘𝑠𝑖
From the properties Tables for W shapes, in part 1 of the AISC LFRD Manual (Compact Section
Criteria), for a W14 x 34, flange b/t = bf/2tf = 7.4, web hc/tw = 43.1. Since web (hc/tw = 37.4) < (λr
= 42.2), a W14 x 43 column is not a slender-element section if Fy = 50 ksi.
4.2. W14 x 43. From the properties Tables for W shapes, for a W14 x 43, flange b/t = bf/2tf =
7.5, web hc/tw = 37.4. In A36 steel, flange λr = 42.2. Since flange (b/t = 7.5) < (λr = 15.8) and web
(hc/tw = 37.4) < (λr = 42.2), a W14 x 43 column is not a slender-element section in A36 steel.
(b) However, if Fy = 50 ksi, flange λr = 13.4. web λr = 35.8. Because web (hc/tw = 37.4) < (λr =
42.2), a W14 x 43 column is a slender-element section if Fy = 50 ksi.
4.3. The welded section in Fig. 4-3. Referring to Table 4-1 and Fig. 4-1, for the flanges of a
welded box section.
λ 𝑟 =
238
√ 𝐹𝑦−𝐹𝑟
= {
238
√36−16.5
= 53.9 𝑖𝑓 𝐹𝑦 = 36 𝑘𝑠𝑖
238
√50−16.5
= 41.1 𝑖𝑓 𝐹𝑦 = 50 𝑘𝑠𝑖

20. 20 | P a g e
For the web: λr =
253
√ 𝐹𝑦
= {
253
√36
= 42.2 𝑖𝑓 𝐹𝑦 = 36 𝑘𝑠𝑖
253
√50
= 35.8 𝑖𝑓 𝐹𝑦 = 50 𝑘𝑠𝑖
For the 18 x 18 in box section in Fig. 4-3, b = hc = 18 in – 2 x
1
2
in = 17 in.
tf = tw = t =
1
2
in ⇒
𝑏
𝑐
=
ℎ 𝑐
𝑡 𝑤
=
17 𝑖𝑛
1
2
𝑖𝑛
= 34.
(a) In A36 steel, b/t and hc/tw < λr in all cases; there are no slender elements.
(b) If Fy = 50 ksi, there are also no slender elements, because b/t and hc/tw < λr in all cases.
In Probs. 4.8 & 4.10, use the alignment chart to determine K. All steel is A36.
4.8. The column shown in Fig. 4-4.
Fig. 4-4 All columns are W14 x 99, 15ft 0 in long; all beams are W21 x 50, 30ft 0 in long. The
webs of all members are in the same plane, as shown.
For the typical column, W14 x 99: 𝐼 𝑥 = 1110 in4. L = 15 ft x 12 in/ft. = 180 in.
𝐼 𝑐
𝑙 𝑐
=
11104
180 𝑖𝑛
= 6.17 in3. For the typical beam, W21 x 50: 𝐼 𝑥 = 948 in4. L = 30 ft x 12 in/ft. = 360 in.

21. 21 | P a g e
𝐼 𝑔
𝑙 𝑔
=
9844
360 𝑖𝑛
= 2.73 in3. According to Eq. [4.1], the alignment chart parameter
G’ =
(𝐼/𝑙)𝑐1+ (𝐼/𝑙)𝑐2
(𝐼/𝑙)𝑔1+ (𝐼/𝑙)𝑔2
, At both the upper (A) and lower (B) joints: GA = GB =
2×6.17𝑖𝑛3
2×2.73𝑖𝑛3
= 2.26.
From Eq. [4.2], G = G' x SRF. Determining SRF (the stiffness reduction factor):
𝑃 𝑢
𝐴 𝑔
=
750 𝑘𝑖𝑝𝑠
29.1𝑖𝑛2
= 25.8 ksi. Interpolating in Table 4-3, SRF = 0.39. At joints A and B, GA = GB = G' x
SRF = 2.26 x 0.39 = 0.88. in. Fig. 4-2, a straight line drawn from GA = 0.88 to GB = 0.88 intersects
with K: 1.3.
4.10. The column shown in Fig. 4-5. Column connection to the footing is (a) rigid, (b) pinned.
The W10 x 33 column is 12ft 0in high; the W16 x 26 beam is 30ft 0 in long. The webs of the
column and the beam are in the plane of the frame.
Fig. 4-5.
For the W10 x 33 column: 𝐼 𝑥 = 170 in4. L = 12 ft x 12 in/ft. = 144 in.
𝐼 𝑐
𝑙 𝑐
=
1704
144 𝑖𝑛
= 1.18 in3. For the W16 x 36 beam: 𝐼 𝑥 = 301 in4. L = 30 ft x 12 in/ft. = 360 in.
𝐼 𝑐
𝑙 𝑐
=
3014
360 𝑖𝑛
= 0.84 in3. From Eq. [4.1], G’A = 1.18/0.84 = 1.41.
𝑃 𝑢
𝐴 𝑔
=
200 𝑘𝑖𝑝𝑠
9.71𝑖𝑛2
= 20.6 ksi.
From Table 4-3, by Interpolating, SRF = 0.72. At joint A, and GA = G’A x SRF = 1.41 x 0.72 = 1.02.
(a) For rigid attachment to the foundation, GB = 1.0. K = 1.3 in Fig. 4-2.
(b) For pin connection to the foundation, GB = 10. Drawing a line in Fig. 4-2 from GA = 1.02 to
GB = 10 indicates that K = 1.9.
4.11. In A36 steel, select a 6-in pipe (see Table 4-5) for a required axial compressive strength of
200 kips; KL = 10.0 ft.
Table 4-5 (6-in Pipe Sections)
A, in2 r, in
Standard Weight 5.58 2.25
Extra strong 8.40 2.19
Double extra strong 15.60 2.06
Try a 6-in standard weight pipe:
𝐾𝑙
𝑟
=
10 𝑓𝑡 ×12𝑖𝑛/𝑓𝑡
2.25 𝑖𝑛
= 53.3. From Table 4-4 by interpolation,
∅ 𝑐 𝑃𝑛 = 26.34ksi. The design strength for this pipe, ∅ 𝑐 𝑃𝑛 = ∅ 𝑐 𝐹𝑐𝑟 = 𝐴 𝑔= 26.34 kips x 5.58 in2 =
147 kips < 200 kips required. Try a 6-in extra strong pipe:

22. 22 | P a g e
𝐾𝑙
𝑟
=
10 𝑓𝑡 ×12𝑖𝑛/𝑓𝑡
2.19 𝑖𝑛
= 54.8. Interpolating in Table 4-4,∅ 𝑐 𝐹𝑐𝑟 = 26.13 ksi. The design strength,
∅ 𝑐 𝑃𝑛 = ∅ 𝑐 𝐹𝑐𝑟 𝐴 𝑔= 26.34 kips/in2 x 8.40 in2 = 219 kips > 200 kips required. This is okay.
4.15. A W10 x 49 column, 10 ft. long, carries a service load of 250 kips. Calculate its axial
shortening.
Shortening, ∆=
𝑃𝑙
𝐸𝐴 𝑔
=
250 𝑘𝑖𝑝𝑠 ×(10 𝑓𝑡 ×12 𝑖𝑛/𝑓𝑡)
29,000 𝑘𝑖𝑝𝑠/𝑖𝑛2 ×14.4 𝑖𝑛2
= 0.072 in.
4.16. The section shown in Fig. 4-3 is used for a 40-ft column; Kx = Kr = 1.0. Determine the
design compressive strength if the steel is A36.
The design compressive strength: ∅ 𝑐 𝑃𝑛 = ∅ 𝑐 𝐹𝑐𝑟 𝐴 𝑔 (E2-1)
The value of ∅ 𝑐 𝐹𝑐𝑟, can be obtained from Table 4-4, it KL/r is known. In this problem
KL = 1.0 x 40.0 ft x 12in/ft = 480 in. r = √
𝐼
𝐴
⇒ A = (18in)2 – (17 in)2 = 35.0 in2.
𝐼𝑥 = 𝐼 𝑦 = 𝐼 =
(18 𝑖𝑛)2−(17 𝑖𝑛)2
12
= 1788 in4. r = √
1788𝑖𝑛2
35𝑖𝑛2
= 7.15 in.
𝐾𝑙
𝑟
=
480 𝑖𝑛
7.15 𝑖𝑛
= 67.2 in.
By interpolation in Table 4-4, for KL/r = 67.2, ∅ 𝑐 𝐹𝑐𝑟 = 24.13 ksi, the design compressive strength:
∅ 𝑐 𝑃𝑛 = 24.13 kips/in2 x 35.0 in2 = 845 kips.
Advantages of using LRFD method
Advantages of using LRFD method and Comparison of ASD and LRFD
 LRFD is another tool for design of steel buildings. It provides flexibility to the designer in
selecting design methodology.
 When dead load is larger as compared to live load then LRFD becomes economical.
 The behavior at the collapse including ductility, warning before failure are considered in
LRFD. This is not directly possible in ASD method because here the structure is
considered at service stage.
 Plastic design concepts may be employed in LRFD method but cannot be applied in ASD
method.
 Every type of load may be given different factor of safety depending upon its probability
of overload, number of occurrences and changes in point of application. But in ASD
same factor of safety is used for different loads.
 Safer structures may result under LRFD method because of considering behavior at
collapse. But behavior at collapse is not considered in ASD method.
Disadvantages of Using LRFD method
 elastic behavior considered for load analysis and ultimate plastic behavior for material
strengths are not compatible. However, percentage difference is less.
 Engineers experienced in ASD have to become familiar with this technique.
 Old books are according to ASD method and become ineffective.
 Validity of previous designs is still to be checked according to ASD.
DESIGN OF COMPACT BEAMS AND OTHER FLEXURAL MEMBERS (FLEXURAL STRENGTH AND
SHEAR STRENGTH)

23. 23 | P a g e
COMPACTNESS: The concept of compactness relates to local buckling. cross sections are
classified as compact, non-compact, or slender-element sections. A section is compact if the
flanges are continuously connected to the web, and the width-thickness ratios of all its
compression elements are equal to or less than λp. Structural steel members with compact
sections can develop their full strength without local instability. In design, the limit state of local
buckling need not be considered for compact members.
Compactness criteria for beams (as stated in Sec. B5 of the AISC LRFD Specification) are given
in Table 5-1 and Fig. 5-2.If the width-thickness ratios of the web and flange in flexural
compression are equal to or less than λp, beam design is by the standard method.
Table 5-1 Limiting Width-Thickness Ratios for Beams
Beam element Width
thickness
ratio
Limiting width thickness
ratio, 𝝀 𝒑
General A36 steel
Flanges of W & other I shapes & channels; b/t 65/√ 𝐹𝑦 10.8
Flanges of square & rectangular box sections;
flange cover plates & diaphragm plates b/w lines
of fasteners or welds
b/t 190/√ 𝐹𝑦 31.7
Webs in flexural compression hc/tw 640/√ 𝐹𝑦 106.7
FLEXURAL BEHAVIOR: The distribution of internal normal strains and stresses on the cross
section of a beam is shown in Fig. 5-3. It is based on the idealized stress-strain diagram for
structural steel in Fig. 5-4, which is a simplified version of the actual stress-strain curves in Fig.
1-2. As shown in Fig. 5-3, the normal strain distribution is always linear. The magnitude of strain
is proportional to the distance from the neutral (or centroid) axis. On one side of the neutral
axis, the fibers of the flexural member are in tension (or elongation); on the other side, in
compression (or shortening). The distribution of normal stresses depends on the magnitude of
the load. Under working loads and until initial yielding, stresses (which are proportional to
strains in Fig. 5-4) are also linearly distributed on the cross section. Beyond initial yielding, the
strain will increase under additional load. The maximum stress, however, is the yield stress Fy.
Yielding will proceed inward, from the outer fibers to the neutral axis, as the load is increased,
until a plastic hinge is formed.

24. 24 | P a g e
Fig. 5-2. Definitions of widths (b and hc)
and thickness (flange thickness t and web
thickness tw) for use in Table 5-1.
Fig. 5-3 Flexural strains and stresses

25. 25 | P a g e
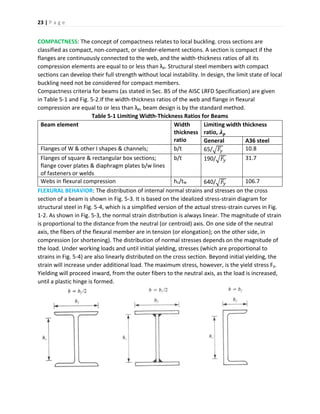
Fig. 5-4 Idealized stress-strain diagram for structural steel
The plastic hinge condition (under which the entire cross section has yielded) represents the
absolute limit of usefulness of the cross section. Only beams which are compact (i.e., not
susceptible to local buckling) and adequately braced (to prevent lateral-torsional buckling) can
attain this upper limit of flexural strength.
The relationships between moment and maximum (extreme fiber) bending stresses, tension or
compression, at a given cross section have been derived in a number of engineering mechanics
textbooks. At the various stages of loading, they are as follows:
Until initial yielding M = Sfb [5.1]
At initial yielding Mr = SFy [5.2]
At full plasticization (i.e. plastic hinge) Mp = ZFy [5.3]
Because of the presence of residual stresses Fr (prior to loading, as a result of uneven cooling
after rolling of the steel member), yielding actually begins at an applied stress of Fy – Fr.
Equation [5.2] should be modified to
Mr = S(Fy – Fr) [5.4]
Equation [5.3] is still valid, however. The plastic moment is not affected by residual stresses.
(Because of their existence in a zero-moment condition before the application of loads, the
tensile and compressive residual stresses must be in equilibrium.)
The terms in Eqs. [5.1] to [5.4] are defined as:
M = bending moment due to the applied loads, kip-in. Mr = bending moment at initial yielding,
kip-in. Mp = plastic moment, kip-in. S = elastic section modulus, in3. Z = plastic section modulus,
in3. Fb = maximum normal stress due to bending, ksi. Fy = specified minimum yield stress, ksi. Fr
= the maximum compressive residual stress in either flange; 10 ksi for rolled shapes;
16.5 ksi for welded shapes.
Elastic section modulus S =
1
𝑐
where I is the moment of inertia of the cross section about its centroid axis, in4; and c is the
distance from the centroid to the extreme fiber, in. The Properties Tables in Part 1 of the AISC
LRFD Manual include the values of I, S, and Z for all the rolled shapes listed.
ELASTIC VERSUS PLASTIC ANALYSIS
Design by either elastic or plastic analysis is permitted by the AISC LRFD Specification (Sec.
A5.1). The more popular elastic analysis has been adopted throughout this text. When an
elastic analysis procedure (such as moment distribution or a typical frame analysis computer
program) is used, the factored moments are obtained assuming linear elastic behavior.
Although this assumption is incorrect at the strength limit states, the fact that elastic analysis is
less complex and is valid under normal service loads has led to its widespread use.
Several restrictions have been placed on plastic design. They are stated in the AISC LRFD
Specification in Secs. A5.1, 85.2, C2.2, EL.2, FL.1, H1.2, and I1.
DESIGN FLEXURAL STRENGTH: Cb = 1.0, Lb ≤ Lr
The design strength of flexural members is øbMn, where do øb = 0.90. For compact sections, the
design bending strength is governed by the limit state of lateral-torsional buckling. As the name

26. 26 | P a g e
implies, lateral-torsional buckling is an overall instability condition of a beam involving the
simultaneous twisting of the member and lateral buckling of the compression flange. To
prevent lateral-torsional buckling, a beam must be braced at certain intervals against either
twisting of the cross section or lateral displacement of the compression flange. Unlike the
bracing of columns (which requires another structural member framing into the column), the
bracing of beams to prevent lateral-torsional buckling can be minimal. Even the intermittent
welding of a metal (floor or roof) deck to the beam may be sufficient bracing for this purpose.
The equations for the nominal flexural strength Mn follow from the preceding discussion of
flexural behavior. Length Lb is defined as the distance between points of bracing. Compact
shapes bending about their minor (or y) axes will not buckle before developing a plastic hinge.
Mny = Mpy = ZyFy [5.6]
For bending about the minor axis regardless of Lb. Compact sections bending about their major
(or x) axes will also develop their full plastic moment capacity without buckling, if Lb ≤ Lp.
Mnx = Mpx = ZxFy [5.7]
For bending about the major axis if Lb ≤ Lp.
Mnx = Mrx = Sx(Fy – Fr) [5.8]
For bending about the major axis if Lb = Lr. If Lp < Lb < Lr, Mn for bending about the major axis is
determined by linear interpolation between Eqs. [5.7] and [5.8]:
𝑀 𝑛𝑥 = 𝑀 𝑝𝑥 − (𝑀 𝑝𝑥 − 𝑀𝑟)= (
𝐿 𝑏−𝐿 𝑝
𝐿 𝑟−𝐿 𝑝
) [5.9]
In the foregoing: Zy = plastic section modulus with respect to the minor centroid (or y) axis, in3
Zx = plastic section modulus with respect to the major centroid (or x) axis, in3
Sx = elastic section modulus with respect to the major centroid (or x) axis, in3
Lengths Lp and Lr are defined in Sec. F1.2 of the AISC LRFD Specification as follows.
For l-shaped sections and channels bending about their major axis
𝐿 𝑝 =
300𝑟 𝑦
√ 𝐹𝑦
(F1-4)
For solid rectangular bars and box beams: 𝐿 𝑝 =
300𝑟 𝑦
𝑀 𝑝
√𝐽𝐴 (F1-5)
where: ry = the radius of gyration with respect to the minor centroid (or y) axis, in
A = cross-sectional area, in2, J = torsional constant, in4
The limiting laterally unbraced length Lr and the corresponding buckling moment Mr are
determined as follows: For I-shaped sections, doubly symmetric and singly symmetric with the
compression flange larger than or equal to the tension flange, and channels loaded in the plane
of the web: 𝐿 𝑟 =
𝑟 𝑦𝑋1
𝐹𝑦−𝐹𝑟
√1 + 𝑋2(𝐹𝑦 − 𝐹𝑟)2 (F1-5)
𝑀𝑟 = (𝐹𝑦 − 𝐹𝑟)𝑆 𝑥 (F1-7)
Where, 𝑋1 =
𝜋
𝑆 𝑥
√
𝐸𝐺𝐽𝐴
2
(F1-8). & 𝑋2 = 4
𝐶 𝑤
𝐼 𝑦
(
𝑆 𝑥
𝐺𝐽
)2
(F1-9)
where

27. 27 | P a g e
E = modulus of elasticity of steel = 29,000 ksi, G = shear modulus of elasticity of steel: 11,200
ksi, Iy = moment of inertia about the minor centroidal (or y) axis, in4, Cw = warping constant, in6.
For symmetric box sections bending about the major axis and loaded in the plane of symmetry,
Mr and Lr shall be determined from formulas (F1-7) and (F1-10), respectively.
For solid rectangular bars bending about the major axis.
𝐿 𝑟 =
57,000𝑟 𝑦
𝑀 𝑟
√𝐽𝐴 (F1-10) & 𝑀𝑟 = 𝐹𝑦 𝑆 𝑥 (F1-11)
Values of J and Cw for many structural shapes are listed in Torsion Properties Tables in Part 1 of
the AISC LRFD Manual.
The practical design of steel beams (Cb = 1.0) can best be done graphically by (1) reference to
the beam graphs in the section entitled Design Moments in Beams, in Part 3 of the AISC LRFD
Manual, where øbMn is plotted versus Lb for Fy = 36 and 50ksi or (2) constructing a graph similar
to Fig. 5-5 from data in the Load Factor Design Selection Table, also in Part 3 of the AISC LRFD
Manual.
BENDING COEFFICIENT Cb
The bending coefficient is defined as
𝐶𝑏 = [1.75 + 1.05
𝑀1
𝑀2
+ 0.3(
𝑀1
𝑀2
)2
] ≤ 2.3. [5.10]
where M1 is the smaller and M2 is the larger end moment for the unbraced segment of the
beam under consideration. If the rotations due to end moments M1 and M2 are in opposite
directions, then M1/M2 is negative; otherwise, M1/M2 is positive. Coefficient Cb = 1.0 for
unbraced cantilevers and for members where the moment within part of the unbraced segment
is greater than or equal to the larger segment end moment (e.g., simply supported beams,
where M1 = M2 = 0). Coefficient Cb accounts for the effect of moment gradient on lateral-
torsional buckling. The LRFD moment capacity equations were derived for a beam with a
constant moment braced only at the supports, failing in lateral-torsional buckling; Cb = 1.0. If

28. 28 | P a g e
the moment diagram between two successive braced points is not constant, the described
region is less susceptible to lateral-torsional buckling; in general, 1.0 ≤ Cb ≤ 2.3.
DESIGN FLEXURAL STRENGTH: 𝐂 𝐛 ≥ 𝟏. 𝟎, 𝐋 𝐛 ≤ 𝐋 𝐫
Incorporating C6 requires modification of Eqs. [5.8] and [5.9]. Equation [5.7] does not change.
𝑀 𝑛𝑥 = 𝑀 𝑝𝑥 = 𝑍 𝑥 𝐹𝑦 (5.7)
for bending about the major axis if. Lb ≤ Lm. However,
𝑀 𝑛𝑥 = 𝐶 𝑏 𝑀𝑟 = 𝐶 𝑏 𝑆 𝑥 (𝐹𝑦 − 𝐹𝑟) ≤ 𝑀 𝑝𝑥 (5.11)
for bending about the major axis if Lb = Lm, and the linear interpolation equation, Eq. [5.9],
becomes: 𝑀 𝑛 = 𝐶 𝑏 [ 𝑀 𝑝 – ( 𝑀 𝑝 − 𝑀𝑟)
𝐿 𝑏−𝐿 𝑝
𝐿 𝑟−𝐿 𝑝
] ≤ 𝑀 𝑝. [F1-3]
for Lm < Lb < Lr. ,. All the terms in the equations are as defined above. The relationships are
shown graphically in Fig. 5-6, where it can be seen that Lm is the unbraced length at which Eqs.
[5.7] and (F 1-3) intersect.
The design of steel beams (1.0 < Cb ≤ 2.3) should be done graphically by developing a plot
similar to that in Fig. 5-6. After determining Cb with Eq. [5.10], one can find the other required
parameters (Lp, øbMp, Lr, and øbMr) in the Load Factor Design Selection Table in Part 3 of the
AISC LRFD Manual.
When Cb > 1.0, there is a twofold advantage in including Cb > 1.0 in Eqs. [5.11] and (F1-3), and
not conservatively letting Cb = 1.0 (as in the graphs in Part 3 of the AISC LRFD Manual): (1) the
unbraced length for which Mn = Mp is extended from Lp to Lm, and (2) for Lb >Lm, the moment
capacity Mn is multiplied by Cb. The reader can find these facts depicted in Fig. 5-6.

29. 29 | P a g e
DESIGN FLEXURAL STRENGTHZ Lb > Lr
If the unbraced length Lb > Lr and Cb = 1.0, elastic lateral-torsional buckling occurs. There is a
significant reduction in the flexural design strength øbMn as Lb increases beyond Lr.
Intermediate bracing should be provided, if possible, to avoid such uneconomical designs.
However, if Lb > Lr
Mn = Mcr ≤ Mp (F1-12)
for bending of a compact section about its major axis.
The critical elastic moment Mcr is defined as follows. For doubly symmetric I-shaped members
and channels loaded in the plane of the web:
𝑀𝑐𝑟 = 𝐶 𝑏
𝜋
𝐿 𝑏
√ 𝐸𝐼 𝑦 𝐺𝐽 + (
𝜋𝐸
𝐿 𝑏
)
2
𝐼 𝑦 𝐶 𝑤 =
𝑆 𝑏 𝑆 𝑥 𝑋1√2
𝐿 𝑏/𝑟 𝑦
√1 +
𝑋1
2 𝑋2
2(𝐿 𝑏/ 𝑟 𝑦)2
(F1-13)
For solid rectangular bars and symmetric box sections
𝑀𝑐𝑟 =
57,000𝐶 𝑏
𝐿 𝑏/ 𝑟 𝑦
√𝐽𝐴 (F1-14)
GROSS AND NET CROSS SECTIONS
Flexural members are usually designed on the basis of their gross sections. According to Sec. Bl
of the AISC LRFD Specification, the rules for beams with holes in the flanges are as follows:
(1) No deduction is made for holes in a given flange if the area of the holes is equal to or less
than 15 percent of the gross area of the flange.
(2) For holes exceeding this limit, only the area of holes in excess of 15 percent is deducted.
DESIGN SHEAR STRENGTH
The shear strength of beams should be checked. Although flexural strength usually controls the

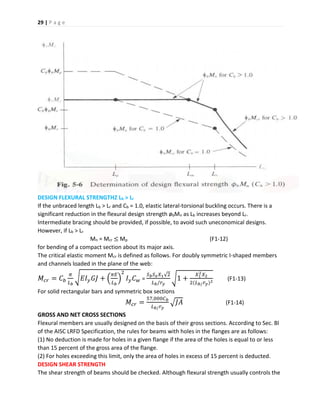
30. 30 | P a g e
selection of rolled beams, shear strength may occasionally govern, particularly for short-span
members or those supporting concentrated loads. In built-up members, the thickness of the
web plate is often determined by shear.
For rolled shapes and built-up members without web stiffeners, the equations in Sec. F2 of the
AISC LRFD Specification can be somewhat simplified, as follows. The design shear strength is
øvVn, where øv = 0.90.
For
ℎ
𝑡 𝑤
≤
418
√ 𝐹𝑦
⇒ 𝑉𝑛 = 0.6 𝐹𝑦 𝐴 𝑤 [5.12]
For
418
√ 𝐹𝑦
<
ℎ
𝑡 𝑤
≤
523
√ 𝐹𝑦
⇒ 𝑉𝑛 = 0.6 𝐹𝑦 𝐴 𝑤
418/√ 𝐹𝑦
ℎ/𝑡 𝑤
[5.13]
Fig. 5-7 Definition of h for various shapes.
For
ℎ
𝑡 𝑤
>
523
√ 𝐹𝑦
, ⇒ 𝑉𝑛 = 𝐴 𝑤
132,000
(ℎ/𝑡 𝑤)2
[5.14]
Where: Vn = nominal shear strength, kips, Aw = area of the web, in2 = dtw
d = overall depth, in, tw = thickness of web, in, h = the following web dimensions, in: clear
distance between fillets, for rolled shapes; clear distance between flanges for welded sections
(See Fig. 5-7.)
The limit states for shear strength are yielding of the web in Eq. [5.12], inelastic buckling of the
web in Eq. [5.13], and elastic buckling of the web in Eq. [5.14].
DISPLACEMENT AND VIBRATION
The two primary serviceability considerations for beams are displacement and vibration.
Traditionally, the maximum deflections of floor beams have been limited to
1
360
of the span
under the service live load specified in the governing building code. Depending on the use of
the member and its span, other deflection criteria (stated in inches or in fractions of the span)
may be more appropriate. Formulas for maximum beam deflections under various loading

31. 31 | P a g e
conditions are given in many textbooks on engineering mechanics and in the AISC LRFD Manual,
Part 3, under the heading Beam Diagrams and Formulas. The most common beam loadings are
shown here in Table 5-2, together with the resulting maximum shears, moments, and
deflections.
Table 5-2 Beam Formulas
Loading Condition Maximum Value Location
Simple beam-uniform load
M =
𝑤𝑙2
8
V =
𝑊𝑙
2
∆ =
5𝑤𝑙2
384𝐸𝐼
Mid-span
Ends
Mid-span
Simple beam-concentrated load at center M =
𝑃𝑙
4
V =
𝑃
2
∆ =
5𝑤𝑙3
48𝐸𝐼
Mid-span
Ends
Mid-span
Simple beam-concentrated load at any point
M =
𝑃𝑎𝑏
𝑙
V =
𝑃𝑎
𝑙
∆ =
𝑃𝑎𝑏(𝑎+2𝑏)√3𝑎(𝑎+2𝑏)
27𝐸𝐼𝑙
Point of load
Right end
𝑥 =
√
𝑎(𝑎+2𝑏)
3
Cantilever beam-uniform load
M =
𝑤𝑙2
2
V = wL
∆ =
𝑤𝑙4
8𝐸𝐼
Fixed end
Fixed end
Free end
Cantilever beam-concentrated load at free end M = PL Fixed end

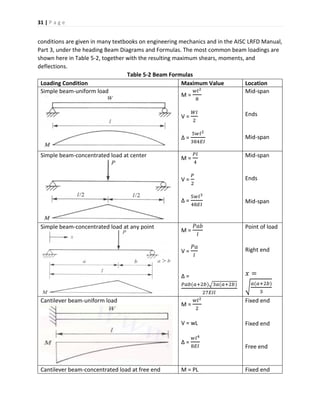
32. 32 | P a g e
V = P
∆ =
𝑃𝑙3
3𝐸𝐼
Fixed end
Free end
Beams that are otherwise satisfactory have occasionally been the cause of annoying floor
vibrations. Particularly sensitive are large open floor areas with long-span beams, free of
partitions and other significant sources of damping, or energy release. To prevent excessive
vibration it has been customary to specify the minimum depth of floor beams as a fraction (e.g.,
1
20
) of their span.
DESIGN OF NON-COMPACT BEAMS AND GIRDERS (FLEXURAL DESIGN AND SHEAR DESIGN)
NON-COMPACT BEAMS
The flexural design strength is øbMn, where øb = 0.90. For non-compact beams, the nominal
flexural strength Mn is the lowest value determined from the limit states of: lateral-torsional
buckling (LTB), flange local buckling (FLB), web local buckling (WLB).
For λp < λ ≤ λr, Mn in each limit state is obtained by linear interpolation between Mn and Mn, as
follows. For the limit state of lateral-torsional buckling,
𝑀 𝑛 = 𝐶 𝑏 [ 𝑀 𝑝 – ( 𝑀 𝑝 − 𝑀𝑟)
𝜆−𝜆 𝑝
𝜆 𝑟−𝜆 𝑝
] ≤ 𝑀 𝑝. [A-F1-2]
For the limit states of flange and web buckling
𝑀 𝑛 = 𝑀 𝑝 – ( 𝑀 𝑝 − 𝑀𝑟) (
𝜆−𝜆 𝑝
𝜆 𝑟−𝜆 𝑝
) [A-F1-3]
For all limit states, if λ ≤ λp, Mn = Mp Expressions for Mp as well as for Mr, λ, λp and λr, in
each limit state, are given in Table 6-1 (which is an abridged version of Table A-F1.1 in APP. F
of the AISC LRFD Specification).
As shown schematically in Fig. 6-1, the flexural design of non-compact beams can be
accomplished by
Looking up in Table 6-1 values for Mp and Mr, λp and λr for each of the relevant limit states.
Graphically interpolating in each case to obtain an Mn for the given λ.
Selecting the minimum Mn as the nominal flexural strength
Table 6-1 Flexural Strength Parameters
Cross Sections 𝑴 𝒑 Limit State 𝑴 𝒓 λ 𝛌 𝒑 𝛌 𝒓
Channels & doubly
& singly symmetric
I-shaped beams
𝐹𝑦 𝑍 𝑥 LTB: doubly
symmetnc
members and
channels
(𝐹𝑦−𝐹𝑟)𝑆 𝑥 𝐿 𝑏
𝑟𝑦
300
√ 𝐹𝑦
See Eqs.
(F1-6), (F1-
8),& (Fl-9)

33. 33 | P a g e
bending about
major axis
LTB: singly
symmetric
members
(𝐹𝑦−𝐹𝑟)𝑆 𝑥𝑐 ≤
𝐹𝑦 𝑆 𝑥𝑡
𝐿 𝑏
𝑟𝑦
300
√ 𝐹𝑦
Value of λ
for which
Mcr = Mr,
with Cb = 1.
FLB (𝐹𝑦−𝐹𝑟)𝑆 𝑥 𝑏
𝑡
65
√ 𝐹𝑦
141
√ 𝐹𝑦−10
for
rolled
shapes
106
√ 𝐹𝑦−16.5
for
welded
shapes
WLB 𝐹𝑦 𝑆 𝑥 ℎ 𝑐
𝑡 𝑤
640
√ 𝐹𝑦
970
√ 𝐹𝑦
Channels and
doubly symmetric
l-shaped members
bending about
minor axis
𝐹𝑦 𝑍 𝑦 FLB 𝐹𝑦 𝑆 𝑥 Same as for major-axis bending
Solid rectangular
bars bending
about major axis
𝐹𝑦 𝑍 𝑥 LTB 𝐹𝑦 𝑆 𝑥 𝐿 𝑏
𝑟𝑦
3570√𝐽𝐴
𝑀 𝑝
57,000√𝐽𝐴
𝑀𝑟
Symmetric box
sections loaded in
a plane of
symmetry
𝐹𝑦 𝑍 LTB (𝐹𝑦−𝐹𝑟)𝑆 𝑥 𝐿 𝑏
𝑟𝑦
3570√𝐽𝐴
𝑀 𝑝
57,000√𝐽𝐴
𝑀𝑟
FLB 𝐹𝑦 𝑆 𝑥 𝑏
𝑡
190
√ 𝐹𝑦
238
√ 𝐹𝑦 − 𝐹𝑟
WLB 𝐹𝑦 𝑆 𝑥 ℎ 𝑐
𝑡 𝑤
640
√ 𝐹𝑦
970
√ 𝐹𝑦

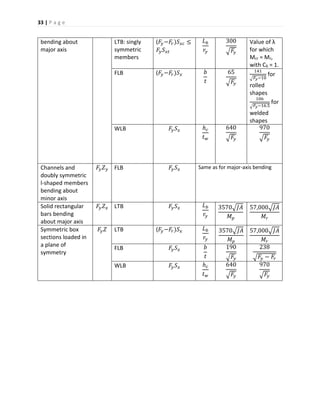
34. 34 | P a g e
Fig. 6-1 Nominal flexural strength of a non-compact beam (example)
Shear capacity should also be checked. The design shear strength is
øvVn, where øv = 0.90 and Vn, the nominal shear strength, is determined from Eq. [5. 12], [5.13],
or [5.14].
The definitions of the terms used above are
λ = slenderness parameter = minor axis slenderness ratio Lb/ry, for LTB = flange width thickness
ratio b/t, defined in Fig. 5-2, for FLB = web depth-thickness ratio hc/tw, defined in Fig. 5-2, for
WLB, λp = the largest value of λ for which Mn = Mp. λr = largest value of λ for which buckling is
inelastic, Mn = nominal flexural strength, kip-in, Mp = plastic moment, kip-in, Mr = buckling
moment at λ = λr, kip-in, Cb = bending factor, as defined in Eq. [5.10], Vn = nominal shear
strength, kips.
Additional terms used in Table 6-1 are Fy = specified minimum yield stress, ksi, Zx = plastic
section modulus about the major axis, in3, Zy = plastic section modulus about the minor axis, in3
Sx = elastic section modulus about the major axis, in3
Sxc = Sx with respect to the outside fiber of the compression flange, in3
Sxt = Sx with respect to the outside fiber of the tension flange, in3, Sy = elastic section modulus
about the minor axis, in3, Lb = laterally unbraced length, in
ry = radius of gyration about the minor axis, in
b, t, hc, tw = dimensions of cross section, defined in Fig. 5-2, in
A = cross-sectional area, in2
J = torsional constant, in4, Fr = compressive residual stress in the flange = 10 ksi for rolled
shapes = 16.5 ksi for welded shapes

35. 35 | P a g e
PLATE GIRDERS: In the AISC LRFD Specification, two terms are used for flexural members: beam
and plate girder. The differences between them are as follows.
Beam Plate Girder
Rolled or welded shape. No web stiffeners
and web
ℎ 𝑐
𝑡 𝑤
≤
970
√ 𝐹𝑦
welded shape web stiffeners or web
ℎ 𝑐
𝑡 𝑤
>
970
√ 𝐹𝑦
, or both
Stiffeners are discussed later in this chapter. Web stiffeners are not required if web hc/tw < 260
and adequate shear strength is provided by the web in accordance with Eqs. [5.12] to [5.14].
(Please note: Two different parameters in the AISC LRFD Specification refer to the clear height
of the web: h and hc. In Sec. B5 of the LRFD Specification they are thus defined:
For webs of rolled or formed sections, h is the clear distance between flanges less the fillet or
corner radius at each flange; hc is twice the distance from the neutral axis to the inside face of
the compression flange less the fillet or corner radius.
For webs of built-up sections, h is the distance between adjacent lines of fasteners or the clear
distance between flanges when welds are used and hc is twice the distance from the neutral
axis to the nearest line of fasteners at the compression flange or the inside face of the
compression flange when welds are used.
The distinction between h and hc is shown in Fig. 6-2, where it can be seen that for doubly
symmetric cross sections, h = hc.)

36. 36 | P a g e
Fig. 6-2 Definitions of h and hc : (a) singly symmetric built-up sections; (b) doubly symmetric
built-up sections
For plate girders, the maximum permissible web slenderness h/tw depends on the spacing of
the stiffeners. If,
𝑏
𝑡
≤ 1.5,
ℎ
𝑡 𝑤
≤
2000
√ 𝐹𝑦
(A-G1-1)
𝑏
𝑡
> 1.5,
ℎ
𝑡 𝑤
≤
14,000
√ 𝐹𝑦(𝐹𝑦+𝐹𝑟)
(A-G1-1)
where a = clear distance between transverse stiffeners, in, tw = web thickness, in Fy = specified
minimum yield stress of steel, ksi, Fr = compressive residual stress in flange: 16.5 ksi for plate
girders. Plate girders are covered in App. G of the AISC LRFD Specification. The stiffening of
slender plate girder webs enables them to exhibit significant post buckling strength through
"tension field action." After the web buckles, a girder acts like a Pratt truss: the stiffeners
become vertical compression members, and the intermediate web panels act as diagonal
tension members.
DESIGN FLEXURAL STRENGTH OF PLATE GIRDERS
The design flexural strength is øbMn, where øb = 0.90. To determine the nominal flexural
strength Mn : if hc/tw ≤ 970√ 𝐹𝑦. If hc/tw > 970√ 𝐹𝑦 (i.e., the web is slender), Mn is
governed by the limit states of tension flange
yielding and compression flange buckling, as follows.
For yielding of the tension flange: 𝑀 𝑛𝑥 = 𝑆 𝑥𝑡 𝑅 𝑃𝐺 𝐹𝑦 (A-G2-1)
For buckling of the compression flange: 𝑀 𝑛𝑥 = 𝑆 𝑥𝑐 𝑅 𝑃𝐺 𝐹𝑐𝑟 (A-G2-2)
The nominal flexural strength Mn is the lower value obtained from these equations, where
𝑅 𝑃𝐺 = 1 – 0.0005 𝑎 𝑟 (
ℎ 𝑐
𝑡 𝑤
−
970
√ 𝐹 𝑐𝑟
) ≤ 1.0 (A-G2-3)
where ar = ratio of web area to compression flange area, Fcr = critical compression flange stress,
ksi, Fy = minimum specified yield stress, ksi, Sxc = elastic section modulus referred to
compression flange, in3, Sxt = elastic section modulus referred to tension flange, in3.
The critical stress Fcr in Eq. (A-G2-2) depends on the slenderness parameters λ, λp, λr, and CPG.
For λ ≤ λ 𝑝 , 𝐹𝑐𝑟 = 𝐹𝑦 (A-G2-4)
For λ 𝑝 < λ ≤ λ 𝑟 𝐹𝑐𝑟 = 𝐶 𝑏 𝐹𝑦 [1 −
1
2
(
𝜆−𝜆 𝑝
𝜆 𝑟−𝜆 𝑝
)] ≤ 𝐹𝑦 (A-G2-5)
For λ ≤ λ 𝑟 𝐹𝑐𝑟 =
𝐶 𝑃𝐺
λ2
(A-G2-6)
The slenderness parameters are determined for both the limit state of lateral-torsional buckling
and the limit state of flange local buckling; the lower value of Fcr governs.
For the limit state of lateral-torsional buckling
λ =
𝐿 𝑏
𝑟 𝑇
(A-G2-7) λ 𝑝 =
300
√ 𝐹𝑦
(A-G2-8)
λ 𝑟 =
756
√ 𝐹𝑦
(A-G2-9) C 𝑃𝐺 = 286,000C 𝑏 (A-G2-10)

37. 37 | P a g e
where Cb is determined from Eq. [5. 10] and rT is the radius of gyration of compression flange
plus one-third of the compression portion of the web taken about an axis in the plane of the
web, in. For the limit state of flange local buckling
λ =
𝑏 𝑓
2𝑡 𝑓
(A-G2-11) λ 𝑝 =
65
√ 𝐹𝑦
(A-G2-12)
λ 𝑟 =
150
√ 𝐹𝑦
(A-G2-13) C 𝑃𝐺 = 11,200 (A-G2-14) C 𝑏 = 1.
The limit state of web local buckling is not applicable.
DESIGN SHEAR STRENGTH OF PLATE GIRDERS
The design shear strength of øv Vn, where øv = 0.90.
For
ℎ
𝑡 𝑤
≤
187
√ 𝑘/𝐹𝑦
𝑉𝑛 , = 0.6 𝐴 𝑤 𝐹𝑦 (A-G3-1)
For
ℎ
𝑡 𝑤
>
187
√ 𝑘/𝐹𝑦
𝑉𝑛 , = 0.6 𝐴 𝑤 𝐹𝑦 (𝐶𝑣 +
1−𝐶 𝑣
1.15√1+(𝑎/ℎ)2
) (A-G3-2)
Except for end panels and where
𝑎
ℎ
> {
3.0
𝑜𝑟
260
(ℎ/𝑡 𝑤)2
[6.1]
In such cases tension field action does not occur and: 𝑉𝑛 , = 0.6 𝐴 𝑤 𝐹𝑦 𝐶𝑣 (A-G3-3)
In the preceding equations: k = 5 +
5
(𝑎/ℎ)2
(A-G3-4)
Except that k = 5.0 if Expression [6.1] is true or if no stiffness are present: Aw is the area of the
web, in2 = dtw; and d is the overall depth, in.
If, 187√
𝑘
𝐹𝑦
≤
𝑘
𝑡 𝑤
≤ 234√
𝑘
𝐹𝑦
, 𝐶𝑣 =
187√ 𝑘/𝐹𝑦
ℎ/𝑡 𝑤
(A-G3-5)
If,
ℎ
𝑡 𝑤
> 234√
𝑘
𝐹𝑦
, 𝐶𝑣 =
44,000 𝑘
(ℎ/𝑡 𝑤)2 𝐹𝑦
(A-G3-6)
WEB STIFFENERS: Transverse stiffeners are required if web h/tw ≥ 260 or web shear strength,
(for unstiffened beams), is inadequate. The stiffeners should be spaced to provide sufficient
shear strength in accordance with the preceding provisions for plate girders.
Additional requirements for stiffeners are: 𝐼𝑠𝑡 ≥ 𝑎𝑡 𝑤
3
𝑗 [6.2]
Whenever stiffeners are required and:
𝐴 𝑠𝑡 ≥
𝐹𝑦
𝐹𝑦.𝑠𝑡
[0.15Dℎ𝑡 𝑤(1 − 𝐶𝑣)
𝑉𝑢
∅ 𝑣 𝑉𝑛
− 18𝑡 𝑤
2
] ≥ 0 (A-G4-2)
For tension field action where: J =
2.5
(𝑎/ℎ)2
– 2 ≥ 0.5. (A-G4-1)
and Ist = moment of inertia of a transverse web stiffener about an axis in the web center for
stiffener pairs or about the face in contact with the web plate for single stiffeners, in4.
Ast = cross-sectional area of a transverse web stiffeners, in2. Fy = specified minimum yield stress
of the girder steel, ksi. Fy.st = specified minimum yield stress of the stiffener material, ksi

38. 38 | P a g e
D = 1.0 for stiffeners in pairs: 1.8 for single angle stiffeners, 2.4 for single plate stiffeners
Vu = required shear strength at the location of the stiffener, ksi and Cv and Vn are as defined
above. Plate girders with webs that depend on tension field action [i.e., their shear strength is
governed by Eq. (A-G3-2)1, must satisfy an additional criterion, flexure-shear interaction.
If, 0.6
𝑉𝑛
𝑀 𝑛
≤
𝑉𝑢
𝑀 𝑢
≤ 1.33
𝑉𝑛
𝑀 𝑛
, Then
𝑀 𝑢
𝑀 𝑛
+ 0.625
𝑉𝑢
𝑉𝑛
≤ 1.24 (A-G5-1)
Must be true, Here, Vu and Mu are the required shear and moment strengths at a cross section
calculated from the factored loads: Vn and Mn are the nominal shear and moment strengths
(𝑉𝑢 ≤ ∅𝑉𝑛 𝑎𝑛𝑑 𝑀 𝑢 ≤ ∅𝑀 𝑛; ∅ = 0.9).
STIFFENER DETAILS: The web stiffeners provided in accordance with the provisions cited in this
chapter may be one-sided or two-sided. If a pair of stiffeners is used, they can be welded to the
web only. Single stiffeners are also welded to the compression flange, as are stiffeners attached
to lateral bracing. The welds connecting stiffeners to girder webs are stopped short of the
flange four to six web thicknesses from the near toe of the web-to-flange weld.
ROLLED VERSUS BUILT.UP BEAMS: Because they are more economical than their welded
equivalents, rolled beams are used whenever possible. Rolled W shapes (the most popular
beams) are available in depths of 4 to 40 in (W4 to W40). Welded girders are used when (1) the
depth must exceed 40 in or (2) the rolled shapes available for the specified depth do not
provide sufficient bending strength (a function of Zx) or stiffness (a function of Ix). Regardless of
whether rolled or welded shapes are utilized, beams are normally oriented to take advantage of
the superior major-axis properties (Zx > Zy, and Ix > Iy).
Difference between Beam and Girder
Basics of Beam Vs. Girder: Beams are horizontal members and one of the most commonly
designed elements of structure typically intended to carry distributed loads such as parallel
walls or tributary areas of the floor and roof systems. It is a structural element capable of
withstanding loads primarily by bending which are used for support in construction projects. A
beam which supports other beams is commonly called a girder, however, it is still a beam.
Girder supports smaller beams and act as the main horizontal support of a structure, designed
to support major concentrated loads such as columns or beam reactions.
Size of Beam Vs. Girder: The key difference between a beam and a girder is the size of the
component. Beams are often referred to as girders in the construction scene and girders are
the main horizontal support structure for smaller beams. So, we can say, all girders are beams,
but not all beams are necessarily girders. Both are bending members distinguished primarily by
the manner in which they are loaded. If it’s the main structural support consisting of smaller
beams, it is a girder. However, there is no strict rules in the Code regarding dimensions that
distinguish a beam from a girder.
Types of Beam Vs. Girder: In engineering, beams are classified into several types based on
many factors. Based on the type of support, beams are mainly classified into following types:
Simply supported, Fixed, Continuous, Cantilever, and Trussed. Beams can be classified based on
geometry as straight beam, curved beam, and tapered beam. Based on the cross section shape,
beams are divided into I-beam, T-beam, and C-beam. A girder is typically used to refer to a steel

39. 39 | P a g e
beam. I-beam girders are the most common type of girders used in bridge construction. Box
girders are mainly used in construction of elevated bridges and roadway flyovers.
Functionality of Beam Vs. Girder: Both beams and girders are horizontal members designed to
support structures by the only deflecting factor, bending. Beams support the structural integrity
of buildings, mostly residential structures and can be found in floors, walls, ceilings, roofs, and
decks. Beams are the choice of structural member because of their incredible load bearing
capacity against all conditions. Girders mainly support smaller beams and are typically used to
construct bridges and flyovers because they are capable of carrying extremely heavy loads.
Girders are mostly used as box or Z shape members as girder bridges which are the most
common and simple bridge type used in construction.
JOIST & SPANDRELS
Joists: Joists can be thought of as several small beams. Joists are basically a horizontal structural
member that runs across an open space. Their function is primarily the same as beams, except
joists are supported by wall framing, foundations, or beams. Joists usually run between walls or
rafters to support a ceiling or floor. They transfer the dead load of the subfloor and floor
finishes as well as the live load of people and furnishings to beams, walls, headers, or
foundation walls. Joists are like the skeleton of a building that supports the load which the floor
is built to bear. Joists are technically beams that typically spans relatively short distances
compared to beams and are made of steel, wood, or engineered wood. OR
Steel members in building structures can be part of the floor framing system to carry gravity
loads, the vertical framing system, the lateral framing system to provide lateral stability to
the building and resist lateral loads, or two or more of these systems. Floor members are
normally called joists, purlins, beams, or girders. Roof members are also known as rafters.
Spandrels: In case of high rise buildings, the masonry walls are usually not able to withstand
their self-weight and the slab weight. In such cases, the beams are provided exterior walls at
each floor level to support the wall load and perhaps some roof load also. These beams are
termed as spandrels.
STRINGERS AND FLOOR BEAMS
Stringers are beams generally placed parallel to the longitudinal axis of the bridge, or direction
of traffic, in highway bridges, such as truss bridges. Usually. they should be framed into floor
beams. But if they are supported on the top flanges of the floor beams, it is desirable
that the stringers he continuous over two or more panels. In bridges with wood floors,
intermediate cross frames or diaphragms should be placed between stringers more than 20
ft. long. In skew bridges without end floor beams, the stringers, at the end bearings, should be
held in correct position by end struts also connected to the main trusses or girders. Lateral
bracing in the end panels should be connected to the end struts and main trusses or girders.
Floor beams preferably should be perpendicular to main trusses or girders. Also, connections to
those members should be positioned to permit attachment of lateral bracing, if required, to
both floor beam and main truss or girder. Main material of floor beam hangers should not be
coped or notched. Built-up hangers should have solid or perforated web plates or lacing.

40. 40 | P a g e
TYPES OF LOADS ON STRUCTURE: The different types of loads coming on the foundation of a
structure are described below.
1. Dead Loads: Dead loads consist of self-weight of the structure (weight of walls, floors, roofs
etc.). The weight of the foundation and footings and all other permanent loads acting on the
structure. These can be computed by finding the weights of cubical contents of the different
materials used for constructing the structure.
2. Live Loads: Live loads consist of moving or variable loads like people, furniture, temporary
stores etc. It is also called super-imposed load.
3. Wind Loads: The Wind acts horizontally on the surfaces of the walls, roofs and inclined roof
of the structure. That means it exerts uniform pressure on the structural components on which
it acts and tends to disturb the stability of the structure. The value of wind loads varies
depending on several factors such as geographical location of the structure, height of the
structure, duration of wind flow etc.
4. Snow Loads: The amount of snow load depends on various factors such as shape and size of
roof structure, roofing materials, location of the structure, insulation of the structure, duration,
and frequency of snow.
5. Seismic Load: These loads are internal forces which act on the structure due to earthquake
developed ground movements.
EARTHQUAKE FORCES
For structural engineers and from a conceptual point of view, earthquakes represent just
another force for which structures need to be designed. Earthquake forces, however, possess
several characteristics that make them unique in comparison with any other forces, such as
gravity, wind, or thermal forces. Earthquake forces are the result of a back and forth, and up
and down motion of the ground that supports a structure. These can be exceptionally larger in
magnitude, can change rapidly and erratically during the duration of the earthquake, and may
be radically different from earthquake to earthquake, from one site to another, from one type
of foundation soil to another, and even from one structure to another.
Effects of earthquakes on structures: Furthermore, earthquake forces depend on the
properties of the structure. This means that if one modifies such properties; one also modifies
the earthquake forces that will affect the structure. It also means that they can change if the
earthquake damages the structure. Most importantly, earthquake forces are unpredictable.
Due to the fact that little is known about the factors that shape the earthquake-generated
ground shaking, the magnitude and characteristics of earthquake forces can only be roughly
estimated at best.
Example: Determine the wind pressure for a bridge (100 years’ life), 22.5 m span, located
about 20 km from Allahabad. Also, find the design wind force in terms of the width b of the
bridge.
Sol: For Allahabad: 𝑉𝑏 = 47 m/s. 𝑘1 = 1.07 (for 100 years)
For 22.5m span bridge located in the outskirts of Allahabad.
𝑘2 = 1.15 (Category 2 Class B), 𝑘3 = 1.0 (Level ground).

41. 41 | P a g e
𝑉𝑧 = 𝑉𝑏 𝑘1 𝑘2 𝑘3 = 47 x 1.07 x 1.15 x 1.0 = 57.83 m/s.
Design wind pressure = 0.6 𝑉𝑧
2
= 0.6 x 57.832 = 2006.58 N/m2.
For wind normal to bridge; 𝐹𝑛 = 𝐶𝑓𝑛 𝑃𝑑 𝑘 𝑙 𝑏 𝐹𝑡 = 𝐶𝑓𝑙 𝑃𝑑 𝑘 𝑙 𝑏
For 𝜃 = 0, and assuming double angle sections for the members.
Force coefficient in the normal direction, 𝐶𝑓𝑛 = 1.6.
Force coefficient in the transverse direction, 𝐶𝑓𝑡 = 0.0.
Let L/b = 5.0; k = 0.66.
Wind force on the bridge, 𝐹𝑛 = 1.6 x 2006.58 x 0.66 x 22.5 x b = 47676 b Newtons = 47.67 b KN.
Example: A steel chimney 3.0 m in diameter situated in a region where the intensity of wind
pressure is 1200 N/m2. Assuming the intensity of wind pressure to be uniform, estimate the
shear due to wind load at a level 15 m below the top of the chimney.
Solution: Design wind load = K P1 A1
Where, K = shape factor = 0.7, P1 = intensity of wind pressure = 1200 N/m2.
A1 = projected area = 3.0m x 15.0m. P = 0.7 x 1200 x (3.0 x 15.0) = 37,800 N = 37.8 KN.
Example: Design a built joint to connect two plates 240 x 12 mm (𝒇 𝒚 = 250 N/mm2) using
ordinary M20 bolts. Arrange the bolts to give maximum efficiency.
Solution: Let us provide a double cover butt joint.
Thickness of cover plate =
5
8
x 12 = 7.5mm = 8mm.
The tensile force (T) the main plate can carry: = bt 𝜎 𝑎𝑡 = 240 x 12 x 0.6 x250/103 = 432 KN.
Shear strength of bolt = 2
𝜋
4
𝑑2
𝜏 𝑣𝑓 = 2 x
𝜋
4
202
x 80/10-3 = 50.265 KN.
Bearing strengthof bolt = dt 𝜎 𝑝𝑓 = 20 x 12 x 250 x 10-3 = 60 KN.
Hence, strength of the bolt = 50.265 KN. Number of bolts required =
432
50.265
= 8.594 ≅ 9.
Provide a dimond joint as shown in Fig. Ex. 2.12.
Example: A butt weld is used to connects two plates 180 mm x 18 mm each. Find out the
stress developed in the weld if it is subjected to a moment of 13000 KN mm.
Solution: Assume the butt weld to be double-U type.
The section modulus of the butt weld =
18 𝑥 1802
6
= 97.2 x 103.
Permissible bending stress, 𝜎 𝑝𝑓 = 165 N/mm2, 𝜎𝑏𝑓.𝑐𝑎𝑙 =
13000 ×103
97.2 ×103
= 133.74 N/mm2 < 165 N/mm2. Which is safe.
Example: A 120 mm diameter and 6 mm thick pipe is welded to a 14 mm plate by fillet weld.
The pipe is subjected to a vertical load of 3 KN at 1.00 m from the welded end and a twisting

42. 42 | P a g e
moment of 1.2 KNm. Design the joint.
Solution: Direct load = 3 KN = 3 x 103 N. Bending moment = 3 x 103 x 1000 = 3 x 106 Nmm.
Twisting moment = 1200 x 103 Nmm. Let t = Effective throat thickness of the weld.
Polar moment inertia, 𝐼𝑧𝑧 = 2πr3t = 2π x 603 x t = 1357168 t mm4.
𝐼𝑥𝑥 =
𝐼 𝑧𝑧
2
=
1357168 𝑡
2
= 678584.01 t mm4.
Shear stress due to direct load =
3 ×103
2𝜋 ×60 × 𝑡
=
7.957
𝑡
N/mm2.
Bending stress due to bending moment =
3 ×106 ×60
67.85 ×104 × 𝑡
=
265.29
𝑡
N/mm2.
This bending stress shall be treated as shear since, the actual failure will be along the throat of
the weld.
Shear stress due to twisting moment =
1200 ×103 × 60
135.7168 × 104 × 𝑡
=
53.05
𝑡
N/mm2.
Combined stress = {(
7.957
𝑡
)
2
+ (
265.29
𝑡
)
2
+ (
53.05
𝑡
)
2
}
1/2
or
270.65
𝑡
= 108
t =
270.65
108
= 2.50 mm ≈̇ 3 mm. Hence, provide a 3 mm fillet weld.
Example: Design a column to support an axial load of 700 KN. The column has an effective
length of 7 m with respect to the x-axis and 5.0 m with respect to the y-axis. Fy = 250 N/mm2.
Solution: Let us assume the allowable axial compressive stress as 85 N/mm2.
A =
700 𝑥 103
85
= 8235.29 mm2. From I.S. Handbook No. 1 try I.S.H.B. 350 @ 661.2 N/m. The
relevant ties of the section are, A = 8591 mm2. 𝑟𝑥𝑥 = 149.3 mm, 𝑟𝑦𝑦 = 53.4 mm.
𝐼 𝑥
𝑟 𝑥𝑥
=
7 𝑥 103
149.3
= 46.885 < 180. Which is safe.
𝐼 𝑦
𝑟 𝑦𝑦
=
5 𝑥 103
53.4
= 93.63 < 180. Which is safe.
For
𝐼 𝑥
𝑟 𝑥𝑥
= 46.885 and 𝑓𝑦 = 250 MPa. 𝜎 𝑎𝑐1 = 134.1805 N/mm2.
Load carrying capacity = 134.1805 x 8591 = 1152.744 kN > 700 kN. Which is all right.
For
𝐼 𝑦
𝑟 𝑦𝑦
= 93.63, and 𝑓𝑦 = 250 MPa, 𝜎𝑎𝑐2 = 86.37 N/mm2.
Load carrying capacity = 86.37 x 8591 = 742004.67 N = 742 KN > 700 KN. Which is safe.
Hence, provide I.S.H.B. 360 @ 661.2 N/m.
4.10. The column shown in Fig. 4-5. Column connection to the footing is (a) rigid, (b) pinned.
The W10 x 33 column is 12 ft. 0 in high; the W16 x 26 beam is 30 ft. 0 in long. The webs of the
column and the beam are in the plane of the frame.
Sol: For the W10 x 33 column: 𝐼𝑥 = 170 in4. ⇒ L = 30 ft. x 12 in/ft. = 360 in.
𝑙 𝑐
𝑙 𝑐
=
170 𝑖𝑛4
144 𝑖𝑛
= 1.18 in3.
For the W16 x 26 beam: 𝐼𝑥 = 301 in4, ⇒ L = 30 ft. x 12 in/ft. = 360 in.
𝑙 𝑐
𝑙 𝑐
=
301 𝑖𝑛4
360 𝑖𝑛
= 0.84 in3.

43. 43 | P a g e
From Eq. [4.1], G’A = 1.18/0.84 = 1.41.
𝑃 𝑢
𝐴 𝑔
=
200 𝑘𝑖𝑝𝑠
9.71 𝑖𝑛2
= 20.6 ksi.
Fig. 4.5
From Table 4-3, by interpolation, SRF = 0.72. At joint A, GA = G’A x SRF = 1.41 x 0.72 = 1.02.
(a) For rigid attachment to the foundation, GB = 1.0. K = 1.3 in Fig. 4-2.
(b) For pin connection to the foundation, GB = 10. Drawing a line in Fig. 4-2 from GA = 1.02
GB = 10 indicates that K = 1.9.
4.12. Determine the design strength of a W8 x 40 column (A36 steel).
𝐾𝑥 𝐿 𝑥 = 𝐾 𝑦 𝐿 𝑦 = 15.0 ft.
For a W8 x 40 section, A = 17.7 in2, 𝑟𝑥 = 3.53 in, 𝑟𝑦 = 2.04 in. Since 𝑟𝑦 < 𝑟𝑥, 𝐾 𝑦 𝑙 𝑦/𝑟𝑦 governs.
𝐾 𝑦 𝐿 𝑦
𝑟 𝑦
=
15 𝑓𝑡 ×12 𝑖𝑛/𝑓𝑡
2.04 𝑖𝑛
= 88.2.
From Table 4-4, ∅ 𝑐 𝐹𝑐𝑟 = 20.32 ksi. The design strength of the column
∅ 𝑐 𝑃𝑛 = 𝛿 𝑐 𝐹 𝑐𝑟 𝐴 𝑔 = 20.32 kips/in2 x 11.7 in2 = 238 kips.
In probs. 5.1 to 5.2, determine whether the given beam is compact: (a) in A36 steel (Fy = 36 ksi),
(b) if Fy = 50 ksi.
5.1. W6 x 15. If the width-thickness ratio of an element is greater than λp, the section is non-
compact. For the flanges of a W shape.
λ 𝑝 =
65
√ 𝐹𝑦
= {
65
√36
= 10.8 𝑖𝑓 𝐹𝑦 = 36 𝑘𝑠𝑖
65
√50
= 9.2 𝑖𝑓 𝐹𝑦 = 50 𝑘𝑠𝑖
For the web of a W shape
λ 𝑝 =
640
√ 𝐹𝑦
= {
640
√36
= 106.7 𝑖𝑓 𝐹𝑦 = 36 𝑘𝑠𝑖
640
√50
= 90.5 𝑖𝑓 𝐹𝑦 = 50 𝑘𝑠𝑖

44. 44 | P a g e
From the Properties Tables for W Shapes, in Part 1 of the AISC LRFD Manual (Compact Section
Criteria): for a W6 x 15: flange
𝑏
𝑡
=
𝑏 𝑓
2 𝑡𝑓
= 11.5, web
ℎ 𝑐
𝑡 𝑤
= 21.16.
Since flange (b/t = 11.5) > (λp = 10.8), the W6 x 15 beam is non-compact in A36 steel. Likewise,
it is non-compact if Fy = 59 ksi.
5.2. W12 x 65. From the Properties Tables for W Shapes, for a W12 x 65.
flange
𝑏
𝑡
=
𝑏 𝑓
2 𝑡𝑓
= 9.9, web
ℎ 𝑐
𝑡 𝑤
= 24.9.
(a) In A36 steel: flange 𝜆 𝑝= 10.8, web 𝜆 𝑝 = 106.7. (See prob. 5.1)
Since flange (b/t = 9.9) < (λp = 10.8), and web (hc/tw =24.9) < (λp = 106.7), a W12 x 65 beam
compact in A36 steel.
(D) However, if Fy = 50 ksi. flange 𝜆 𝑝= 9.2, web 𝜆 𝑝 = 90.5. (See prob. 5.1)
Because flange (b/t = 9.9) > (λp = 9.2), a W12 x 65 beam is non-compact if Fy = 50 ksi.
5.7. For the same W24 x 76 beam in major-axis bending, laterally braced at its centerline,
with either a uniform load or a concentrated load at the center, determine the flexural design
strength.
𝐶 𝑏 = [1.75 + 1.05
𝑀1
𝑀2
+ 0.3 (
𝑀1
𝑀2
)
2
] ≤ 2.3
According to Eq. [5-10]:
For either unbraced half of the beam under either loading indicated, M1 = 0 and
M2 > 0; M1/M2 = 0. In Eq. [5-10], Cb = (1.75 + 1.05 x 0 + 0.3 x 0) = 1.75.
For all Lb, the design flexural strength for 𝐶 𝑏 = 1.75, ∅ 𝑏 𝑀 𝑛𝑥( 𝐶 𝑏 = 1.75) = 1.75 x ∅ 𝑏 𝑀 𝑛𝑥( 𝐶 𝑏 =
1.0) ≤ ∅ 𝑏 𝑀 𝑝𝑥. The previous ( 𝐶 𝑏 = 1.0) design flexural strengths are multiplied by ( 𝐶 𝑏 = 1.75);
however, the plastic moment strength (∅ 𝑏 𝑀 𝑝𝑥 = 540kip-ft) cannot be exceeded.
5.8. Select the most economical rolled shape for a27-ft simply supported floor beam. The
upper (compression) flange of the beam is adequately welded to the floor deck at 1 ft 0 in
intervals. Dead load supported by the beam (including its own weight) is 1.3 kips per linear
foot; live load is 2.6 kips per linear foot. Steel is A36. Assume:
(a) There is no member depth limitation. (b) The deepest (architecturally allowable) member is
a W21. (c) The deepest desired member is a W18.
For the case of dead load and floor live load only, the critical load combination formula is
(A4-2): 1.2D + 1.6L + 0.5(Lr or S or R) = 1.2 x 1.3 kips/ft + 1.6 x 2.6 kips/ft + 0 = 5.7 kips/ft
For uniformly distributed loads, maximum M = wl2 / 18 and V = wl2.
Required 𝑀 𝑢 =
5.7 𝑘𝑖𝑝𝑠/𝑓𝑡 ×(27𝑓𝑡)2
8
= 521 kip-ft.
Required 𝑉𝑢 = 5.7
𝑘𝑖𝑝𝑠
𝑓𝑡
×
27𝑓𝑡
2
= 77 kips.
Here, Lb = 1.0 < Lp (all rolled shapes).
(a) In Table 5-3, as in the beam Selection Table in the LRFD Manual, the most economical beams
appear in boldface print. Of those beams, the one of least weight for which ∅ 𝑏 𝑀 𝑛= ∅ 𝑏 𝑀 𝑝 ≥

45. 45 | P a g e
521 kip-ft. is a W24 x 76.
Checking shear strength with Eq. [5.12], for
ℎ
𝑡 𝑤
≤ (418/√ 𝐹𝑦 = 418/√36 =) 69.7.
𝑉𝑛 = 0.6𝐹𝑦 𝐴 𝑤 = 0.6 x 36 ksi x 𝑑𝑡 𝑤
∅ 𝑣 𝑉𝑛 = 0.90 x 9.6 x 36 ksi 𝑑𝑡 𝑤 = 19.4 ksi x 𝑑𝑡 𝑤
For a W24 x 76,
ℎ
𝑡 𝑤
= 49.0 < 69.7. (See Properties Tables for W Shapes in the AISC LRFD Manual,
part 1.) Then ∅ 𝑣 𝑉𝑛 = 19.4 ksi x 23.92 in x 0.440 in = 205 kips > 77 kips required. Use a W24 x 76.
(b) By inspection of Table 5-3, the least-weight W21 for which ∅ 𝑏 𝑀 𝑛𝑥 = ∅ 𝑏 𝑀 𝑝𝑥 ≥ 521
kip/ft is a W21 x 83. Checking shear: ∅ 𝑣 𝑉𝑛 = 19.4 ksi x 𝑑𝑡 𝑤.. For a W21 x 83, ∅ 𝑣 𝑉𝑛 = 19.4 ksi x
21.43 in x 0.515 in = 214 kips > 77 kips required. Use a W21 x 83.
(c) By inspection of Table 5-3, the least-weight W18 for which Q6M* : ∅ 𝑣 𝑉𝑛= 521 kip-ft. is a
W18 x 97. Checking shear: ∅ 𝑣 𝑉𝑛= 19.4 ksi x 𝑑𝑡 𝑤. For a W18 x 97, ∅ 𝑣 𝑉𝑛 = 19.4 ksi x 18.59 in x
0.535 in = 193 kips > 77 kips required. Use a W18 x 97.
(Note: In lieu of calculations, the design shear strengths ∅ 𝑣 𝑉𝑛 for W shapes can be found
tabulated in the section Uniform Load Constants in Part 3 of the AISC LRFD Manual.)
5.14. Simply supported 30-ft-long floor beams, W18 x 35, are spaced 10 ft. 0 in center-to-
center. What is their maximum deflection under a live load of 50lb/ft2?
Sol: w = 50
𝑙𝑏
𝑓𝑡2
x 10 ft. = 500
𝑙𝑏
𝑓𝑡
= 0.5
𝑘𝑖𝑝𝑠
𝑓𝑡
. For a W18 x 35 beam, 𝐼𝑥 = 510 in. From Table 5-2, for
a uniformly loaded simply supported beam, the maximum deflection.
∆=
5𝑤𝑙2
384𝐸𝐼
=
5×0.5
𝑘𝑖𝑝𝑠
𝑓𝑡
×(30𝑓𝑡)4
384×29,000
𝑘𝑖𝑝𝑠
𝑖𝑛2 ×510𝑖𝑛2
× (12 𝑖𝑛/𝑓𝑡)3
= 0.62 in.
∆= 0.62𝑖𝑛 <
𝐿
360
=
30 𝑓𝑡 ×12𝑖𝑛/𝑓𝑡
360
= 1.0 in.
Since live load Deflection: It should generally be acceptable.
5.15. Determine the maximum deflections of the same W18x35 beams under concentrated
loads of 7.5 kips at mid-span. From Table 5-2, for a concentrated load on a simply supported
beam at mid-span; the maximum deflection
∆=
𝑝𝑙3
48𝐸𝐼
=
7.5 𝑘𝑖𝑝𝑠 ×(30𝑓𝑡)3×(12 𝑖𝑛𝑓𝑡)3
48 × 29,000
𝑘𝑖𝑝𝑠
𝑖𝑛2 × 510𝑖𝑛2
= 0.49 in.
6.6. Determine the minimum web thickness for the plate girder in Fig. 6-3, both with and
without web stiffeners; assume, A36 steel. According to the AISC LRFD Specification (App. G),
in unstiffened girders h/tw must be less than 260.
ℎ
𝑡 𝑤
< 260 implies that 𝑡 𝑤 >
ℎ
260
=
56 𝑖𝑛
260
= 0.22 in.
In stiffened girders (a/h ≤ 1.5):
ℎ
𝑡 𝑤
≤
2000
√ 𝐹𝑦
=
2000
√36
= 333
In stiffened girders (a/h > 1.5):
ℎ
𝑡 𝑤
≤
14,000
√ 𝐹𝑦(𝐹𝑦 + 16.5)
=
14,000
√36(36 + 16.5)
= 322

46. 46 | P a g e
The minimum web thickness: 𝑡 𝑤 >
ℎ
333
=
56 𝑖𝑛
333
= 0.17 in.
if the stiffeners are closely spaced (a/h ≤ 1.5). The theoretical minimum web thicknesses for this
plate girder are 0.22 in. if not stiffened and 0.17 in. if stiffened. However, because of the need
to weld (the flange plates and stiffeners) to the web, a web thickness of less than j in is in-
advisable.
7.2. Determine the maximum axial tension that can be sustained by a continuously braced
W10 x 19 beam with a required flexural strength Mux = 54kip-ft; A36 steel. Given are
Mux = 54 kip-ft and Muy = 0.
For a W10 x 19: ∅ 𝑡 𝑃𝑛 = ∅ 𝑡 𝐹𝑦 𝐴 𝑔 = = 0.90 x 36
𝑘𝑖𝑝𝑠
𝑖𝑛2
x 5.62 in2 = 182 kips.
Since Lb = 0. < Lp ∅ 𝑏 𝑀 𝑛𝑥 = ∅ 𝑏 𝑀 𝑝 = 58.3 kip-ft. (A36 steel) as listed in the Beam Selection Table
in the AISC LRFD Manual.
𝑀 𝑢𝑥
∅ 𝑏 𝑀 𝑛𝑥
=
54 𝑘𝑖𝑝 − 𝑓𝑡
58.3 𝑘𝑖𝑝 − 𝑓𝑡
= 0.93
Inspection of Formulas (H1-1a) and (H1-1b) indicates that ( 𝑃𝑢/∅ 𝑡 𝑃𝑛) < 0.2 is required.
Consequently, the latter interaction formula governs.
𝑃 𝑢
2∅ 𝑏 𝑃 𝑛
=
𝑀 𝑢𝑥
∅ 𝑏 𝑀 𝑛𝑥
+
𝑀 𝑢𝑦
∅ 𝑏 𝑀 𝑛𝑦
≤ 1.0 =
𝑃 𝑢
2×182 𝑘𝑖𝑝𝑠
+ (0.93 + 0) ≤ 0. 𝑃𝑢 ≤ 26 𝑘𝑖𝑝𝑠
The maximum required (or factored) axial tensile force is 26 kips.
8.4. In A36 steel, select a W12 section for a beam-column (in a symmetric unbraced frame;
K : 1.2) with the following factored loads: Pu = 400 kips; first-order Mltx = 100 kip-ft due to
wind, all other moments equal zero. Member length is 12 ft. The allowable story drift index
(∆oh/L) is
1
400
, or 0.0025, as a result of a total horizontal (un-factored) wind force of 80kips.
The total factored gravity load above this story is 4800 kips.
Given: 𝑃𝑢 = 400 kips, 𝑀 𝑢𝑦 = 0. 𝑀 𝑛𝑡𝑥 = 100 kips-ft. , ∑ 𝑃 𝑢 = 4800 kips, ∆ 𝑜ℎ/𝐿 = 0.0025, ∑ 𝐻 = 80
kips, KL = 1.2 x 12 ft. = 14.4 ft.

47. 47 | P a g e
From Eq. (H1-2), 𝑀 𝑢𝑥 = 𝐵2 𝑀𝑙𝑡𝑥 , where [according to Eq. (H1-5)]
𝐵2 =
1
1−
∑ 𝑃 𝑢
∑ 𝐻
(
∆ 𝑜ℎ
𝐿
)
=
1
1−
4800 𝑘𝑖𝑝𝑠
80 𝑘𝑖𝑝𝑠(0.0025)
= 1.18.
The second-order required flexural strength Mux = 1.18 x 100 kip-ft = 118 kip-ft. Selecting a trial
W12 shape with Eq. [8.2], we obtain: 𝑃𝑢.𝑒𝑓𝑓 = 𝑃𝑢 + 𝑃𝑢𝑥 𝑚 + 𝑀 𝑢𝑦 𝑚𝑈.
Where for a W12 (KL = 14.4 ft), m = 2.4 and U = 1.5. 𝑃 𝑢. 𝑒𝑓𝑓 = 400 + 118 x 2.4 + 0 = 683 kips.
By interpolation in the Column Load Tables of the AISC LRFD Manual (p. 2-24), if Fy = A36 ksi
and KL = 14.4 ft. ∅ 𝑐 𝑃𝑛 = 732 kips (> 𝑃 𝑢. 𝑒𝑓𝑓 = 43 kips) for a W12 x 96.
Selecting the appropriate beam-column interaction formula, (H1-1a) or (H1-1b), we obtain:
𝑃𝑢
∅ 𝑐 𝑃𝑛
=
400 𝑘𝑖𝑝 − 𝑓𝑡
732 𝑘𝑖𝑝 − 𝑓𝑡
= 0.55 > 0.2
Use formula (H1-1a), which, for 𝑀 𝑢𝑦 = 0, reduces to
𝑃𝑢
∅ 𝑐 𝑃𝑛
+
8
9
𝑀 𝑢𝑥
∅ 𝑏 𝑀 𝑛𝑥
≤ 1.0
The design flexural strength ∅ 𝑏 𝑀 𝑛𝑥 for a W12 x 96 can be determined from the Beam
Selection Table on page 3-15 of the AISC LRFD Manual: because (Lb = 12 ft.) < (Lp = 12.9 ft.),
∅ 𝑏 𝑀 𝑛𝑥 = ∅ 𝑏 𝑀 𝑝 = 397 kip-ft. as tabulated. Substituting in the interaction formula:
0.55 +
8
7
×
118 𝑘𝑖𝑝−𝑓𝑡
397 𝑘𝑖𝑝−𝑓𝑡
≤ 1.0 = 0.55 + 0.26 = 0.81 < 1.0.
By a similar solution of interaction formula (H1-1a), it can be shown that a Wl2 x 87 and a
W12 x 79 are also adequate.
10.5. A W18 x 40 interior beam is shown in Fig. 10-5. Steel is A36, beam span is 30 ft. 0 in, and
beam spacing is 10 ft. 0 in. The beams are to act compositely with a 5-in normal-weight
concrete slab; f’c = 5.0 ksi.
Fig. 10-5
(a) For an interior beam, the effective slab width on either side of the beam centerline is the
minimum of
𝐿
8
=
30.0 𝑓𝑡
8
= 3.75 ft = 45 in.
𝑠
2
=
10.0 𝑓𝑡
2
= 5 ft. The effective slab width is 2 x 45 in = 90 in.
(b) In positive moment regions, Vh for full composite action is the smaller of

48. 48 | P a g e
0.85f’c Ac = 0.85 x 5 ksi x (90 in x 5 in) = 1913 kips. AsFy = 11.8 in2 x 36 ksi = 425 kips
Vh = 425 kips. (c) The nominal strength of a single shear stud [from Eq. (15-1)] is
𝑄 𝑛 = 0.5𝐴 𝑠𝑐√𝑓′ 𝑐 𝐸𝑐 ≤ 𝐴 𝑠𝑐 𝐹𝑢 , For a
3
4
− 𝑖𝑛 − 𝑑𝑖𝑎𝑚𝑒𝑡𝑒𝑟 𝑠𝑡𝑢𝑑,
𝐴 𝑠𝑐 = 𝜋 (
0.75 𝑖𝑛
2
)
2
= 0.44 in2, 𝐸𝑐 = 𝑤1.5
√𝑓′ 𝑐 = 1451.5
√5.0 = 3904 ksi, Fu = 60 ksi.
𝑄 𝑛 = 0.5 × 0.44𝑖𝑛2
√5.0 𝑘𝑠𝑖 × 3904 𝑘𝑠𝑖 ≤ 0.44 𝑖𝑛2
× 60 𝑘𝑠𝑖 = 30.9 kips ≤ 26.4
kips. = 26.5 kips per stud. For the beam shown in Fig. 10-6, the required number of shear
studs is 2n = 2 x 17 = 34.
Fig. 10-6
Assuming a single line of shear studs (over the beam web), stud spacing=30.0 ft/34 = 0.88ft =
10.6 in. This is greater than the six-stud diameter (or 6 x
3
4
in = 4.5in) minimum spacing, and less
than the eight slab thickness (or 8 x 5 in : 40 in) maximum spacing, which is satisfactory.
10.7. Assume the beams in Fig. 10-5 are cantilever beams: A36 steel, with a cantilever span of
8 ft 0 in. Slab reinforcement is No.4 bars (Ar = 0.20 in2 per bar) at 1 ft 0 in center-to-center. Bars
are Grade 60 steel. (a) For an interior beam, the effective slab width on either side of the beam
centerline is the minimum of
L
8
=
8.0 ft
8
= 1.0 ft. .
𝑠
2
=
10.0 𝑓𝑡
2
= 5 ft.
The effective slab width is 2 x 1.0 ft = 2.0 ft.
(b) In negative-moment regions (such as cantilevers): Vh = ArFyr for full composite action, where
Ar and Fyr are the cross-sectional area and minimum yield stress of the reinforcement,
respectively. Because the slab is in tension, the concrete cannot participate in composite
action. For an effective slab width of 2.0 ft.
𝐴 𝑟 =
0.20 𝑖𝑛2
𝑏𝑎𝑟
×
1 𝑏𝑎𝑟
𝑓𝑡
x 2.0 ft. width = 0.40 in2. 𝑉ℎ = 0.40 in2 x 60 ksi = 24 kips.
(c) The nominal strength of a single shear stud is Qn = 26.4 kips. Although n = Vh/Qn =
24kips / 26.4 kips per stud = 0.9 would indicate that one stud is satisfactory, the actual number
of shear studs is governed by the maximum spacing of eight times the slab thickness:
𝑛 =
𝑠𝑝𝑎𝑛
𝑚𝑎𝑥𝑖𝑚𝑢𝑚 𝑠𝑝𝑎𝑛
=
8.0 𝑓𝑡 𝑋 12 𝑖𝑛/𝑓𝑡
8 𝑋 5 𝑖𝑛
= 2.4 or 3 shear studs.
11.7. Determine the design tensile strength of a
7
8
in-diameter bolt if it is (a) A325, (b) A490,
(c) A307. The nominal cross-sectional area of a
7
8
-in-diameter bolt is

49. 49 | P a g e
𝐴 = 𝜋 (
𝐷
2
)
2
= 𝜋 (
7
8
𝑖𝑛
2
)
2
= 0.60 in2
.
The design tensile strength of a bolt: ∅𝑃𝑛 = ∅𝐹𝑡𝑛 𝐴
Where ø = 0.75 and 𝐹𝑡𝑛 is as listed in Table 11.5.
(a) For a
7
8
-in-diameter A325 bolt, the design tensile strength
∅𝑃𝑛 = 0.75 x 90
𝑘𝑖𝑝𝑠
𝑖𝑛2
x 0.60 in2 = 40.6 kips.
(b) For a
7
8
-in-diameter A490 bolt, the design tensile strength
∅𝑃𝑛 = 0.75 x 112.5
𝑘𝑖𝑝𝑠
𝑖𝑛2
x 0.60 in2 = 50.7 kips.
(c) For a
7
8
-in-diameter A307 bolt, the design tensile
∅𝑃𝑛 = 0.75 x 45.0
𝑘𝑖𝑝𝑠
𝑖𝑛2
x 0.60 in2 = 20.3 kips.
11.14. Design a base plate for a W14 x 90 column with a factored axial load of 700 kips. All
steel is A36. The base plate is on a footing 2 ft 0 in x 2 ft 0 in; f’c = 4 ksi.
The design bearing strength for steel bearing on concrete is determined from Eq. (11.5) or
(11.6); the former for bearing on the full area of concrete, and the latter for bearing on less
than the full area. The dimensions of the W14 x 90 column d bf = 14.02 in x 14.52 in. Try a 16 in
x 16 in base plate and use Eq. (11.7).
𝐴2 = 24 in x 24 in = 576 in2. 𝐴1 = 16 in x 16 in = 256 in2
𝑓′ 𝑐 = 4
𝑘𝑖𝑝𝑠
𝑖𝑛2
, ø = 0.60. The design bearing strength: ∅𝑐 𝑃 𝑝 = 0.85𝑓′ 𝑐
𝐴1√
𝐴1
𝐴2
= 0.85 x 4
𝑘𝑖𝑝𝑠
𝑖𝑛2
x 256 in2 x √
576 𝑖𝑛2
256 𝑖𝑛2
= 1306 kips > 700 kips required.
N = 16.0 in, d = 14.0 in, m = 0.5(N – 0.95 d) = 0.5(16 in – 0.95 x 14 in) = 1.35 in.
B = 16.0 in, bf = 14.52 in, n = 0.5(B – 0.80 bf) = 0.5(16 in – 0.80 x 14.52 in) = 2.19 in.
To determine c, solve Eqs. [11.8] to [11.10].
𝑃𝑜 =
𝑃 𝑢
𝐵𝑁
𝑏𝑓 𝑑 =
700 𝑘𝑖𝑝𝑠
16 𝑖𝑛 ×16 𝑖𝑛
x 14.02 in x 1.52 in = 556 kips.
𝐴 𝐻 =
𝑃𝑜
0.6(0.85√ 𝐴2/𝑏𝑓 𝑑𝑓′ 𝑐)
≥
𝑃𝑜
0.6(1.7𝑓′
𝑐
)
=
556 𝑘𝑖𝑝𝑠
0.6(0.85
√
576𝑖𝑛2
(14.52 𝑖𝑛 × 14.0 𝑖𝑛)4
𝑘𝑖𝑝𝑠
𝑖𝑛2
≥
556 𝑘𝑖𝑝𝑠
0.6 × (1.7 × 4
𝑘𝑖𝑝𝑠
𝑖𝑛2 )
= 162 𝑖𝑛2
≥ 136𝑖𝑛2
= 162𝑖𝑛2

50. 50 | P a g e
C =
1
4
[(𝑑 + 𝑏𝑓 + 𝑡𝑓) − √(𝑑 + 𝑏𝑓 + 𝑡𝑓) − 4(𝐴 𝐻 + 𝑡𝑓 𝑏𝑓)]
(𝑑 + 𝑏𝑓 + 𝑡𝑓) = (14.02 + 14.52 – 0.71) in = 27.83 in.
C =
1
4
[27.83 𝑖𝑛 − √(27.83 𝑖𝑛)2 − 4(162 𝑖𝑛2 − 0.71 𝑖𝑛 × 14.52))] c = 4.26 in.
Referring to Eq. [11.8]: m = 1.35 in, n = 2.19 in c = 4.26 in
√
2𝑃𝑢
0.92𝐹𝑦 𝐴 𝐻
= √
2 × 700 𝑘𝑖𝑝𝑠
0.9 × 3 𝑘𝑖𝑝𝑠/𝑖𝑛2 × 16 𝑖𝑛 × 16 𝑖𝑛
= 0.41
√
2𝑃𝑜
0.92𝐹𝑦 𝐴 𝐻
= √
2 × 556 𝑘𝑖𝑝𝑠
0.9 × 3 𝑘𝑖𝑝𝑠/𝑖𝑛2 × 162 𝑖𝑛2
= 0.46
Base plate thickness tp is the largest of (1.35 in x 0.41 = 0.55 in), (2.I9 in x 0.41 = 0.90 in), and
(4.26 in x 0.46 = 1.96 in). Use a base plate 16 in x 2 in x 16 in.
12.4. Determine the maximum load that can be hung from a plate (12 in long x 7 in wide)
welded to the bottom flange of a W18 x 50 beam. All steel is A36.
For a concentrated tensile force acting on the bottom flange of a beam, the applicable limit
states are (1) local web yielding and (5) local flange bending. The corresponding equations are
(K1-2) and (K1-1). In solving Eq. (K1-2) for a W18 x 50 with a 12-in load bearing (in Prob. 12.3) it
was determined that Pu = 233 kips. Because the width of plate = 7 in > 0.15bf (= 0.15 x 7.495 in =
1.12 in), Eq. (K1-1) must be checked:
𝑃𝑢 ≤ ∅𝑅 𝑛 = 0.90 x 6.25 𝑡𝑓
2
𝐹𝑦 = 0.90 x 6.25(0.570 in)2 x 36 ksi. 𝑃𝑢 ≤ 66 kips.
The maximum (factored) hanging load is 66 kips, based on the limit state of local flange
bending. If stiffeners are provided or if the hanging load is confined to the central
0.15bf (= 1.12 in) of the beam flange, 233 kips can be hung.
What are the merits and demerits of welded connections?
Merits: 1) Due to the absence of gusset plates, connecting angles etc. Welded structures are
lighter. 2) The absence of making holes for fasteners, making welding process quicker. 3)
Welding is more adaptable than bolting or riveting. For example, even circular tubes can be
easily connected by welding.
Demerits: 1) Due to uneven heating and cooling members are likely to distort in the
process of welding. 2) There is a greater possibility of brittle fracture in welding. 3) A welded
joint fails earlier than bolted joint, if the structure is under fatigue stresses.
Example: Design a suitable fillet welded joint between two plates of size 160 mm x 8 mm, and
200 mm x 8 mm to developed the full strength of the smaller plate in tension. Assume
permissible tensile stress in plate = 1500 kg/cm2.

51. 51 | P a g e
Sol: Strength of 160 mm x 8 mm plate = 16 x 0.8 x 1500 = 18,432 kg.
Maximum size of fillet weld = 8 – 1.5 = 6.5 mm say 6 mm.
Strength per cm length of the weld = 1 x 0.7 x 0.6 x 1025 = 430 kg.
Total length of the weldrequired =
18,432
430
= 42.87 cm or say 43 cm.
Example 1: A W12 x 50 is used as a column to support a compressive load of 145 kips. The
length is 20 ft. and the ends are pinned. Without regard to LRFD or ASD investigate the
stability of the column.
Sol: For a W12 x 50, Minimum: r = 𝑟𝑦 = 1.96 in. Maximum:
𝐿
𝑟
=
𝐿
𝑟 𝑦
=
20(12)
1.96
= 122.4.
𝑃𝑐𝑟 =
𝜋2 𝐸𝐴
(𝐿∕𝑟)2
=
𝜋2(29,000)(14.6)
(122⋅4)2
= 278.9 kips 𝑃𝑐𝑟 = 278.9 kips > 145 kips. OK – Column is Stable.
Example 2: A W12 x 50 is used as a column to support a compressive load of 145 kips. The
length is 20 ft. the bottom is fixed and the top is free. Without regard to LRFD or ASD
investigate the stability of the column.
Sol: For a W12 x 50, Minimum: r = 𝑟𝑦 = 1.96 in. Maximum:
𝐿
𝑟
=
𝐿
𝑟 𝑦
=
20(12)
1.96
= 122.4.
𝑃𝑐𝑟 =
𝜋2 𝐸𝐴
(𝐾𝐿∕𝑟)2
=
𝜋2(29,000)(14.6)
((2.1)(122⋅4))2
= 63.248 kips 𝑃𝑐𝑟 = 63.248 kips < 145 kips.
NG – Column is Unstable.
Example 3: A W14x74 of A992 steel has a length of 20 feet and pinned ends. Compute the
design strength for LRFD and the allowable compressive strength for ASD
Sol: Slenderness Ratio: 4.71√ 𝐸
𝐹𝑦
= √
29,000
50
= 113. Maximum
𝐾𝐿
𝑟
=
𝐾𝐿
𝑟 𝑦
=
(1)(20)(12)
2.48
= 96.77
< 200.
𝐾𝐿
𝑟
< 4.71√
𝐸
𝐹𝑦
⇒ Inelastic Buckling.
𝐹𝑒 =
𝜋2 𝐸
(𝐾𝐿∕𝑟)2
=
𝜋2(29,000)
(96.77)2
= 30.56 ksi. 𝐹𝑐𝑟 = 0.658
𝐹𝑦
𝐹𝑒
= 0.658
50
30.56
= 25.21 ksi.
𝑃𝑛 = 𝐹𝑐𝑟 𝐴 𝑔 = 25.21(21.8) = 549.6 kips.
LFRD: ∅ 𝑐 𝑃𝑛 = 0.9 𝐹𝑐𝑟 𝐴 𝑔 = (0.9) 549.6 = 495 kips.
ASD: 𝐹𝑎 = 0.6 𝐹𝑐𝑟 = (0.6)(25.21) = 15.31 ksi. 𝐹𝑎 𝐴 𝑔 = 15.31(21.8) = 330 kips.
Example: Determine the total LFRD design strength and total ASD allowable strength of the
5/16-in E70 fillet welds shown in Fig. 14.15.

52. 52 | P a g e
Sol: Effective throat t = (0.707)(
5
16
𝑖𝑛) = 0.221 in.
𝑅 𝑤𝑙 = 𝑅 𝑛 for side welds = 𝐹𝑛𝑤 𝐴 𝑤𝑒 = (0.60 x 70 ksi)(2 x 8 in x 0.221 in) = 148.5 k.
𝑅 𝑤𝑡 = 𝑅 𝑛 for transverse end welds = 𝐹𝑛𝑤 𝐴 𝑤𝑒 = (0.60 x 70 ksi)(10 in x 0.221 in) = 92.8 k.
Applying AISC Equations J2-10a % J2-10b.
𝑅 𝑛 = 𝑅 𝑛𝑤𝑙+ 𝑅 𝑛𝑤𝑡 = 148.5 k + 92.8 k = 241.3 k.
𝑅 𝑛 = 0.85𝑅 𝑛𝑤𝑙+ 1.5𝑅 𝑛𝑤𝑡 = (0.85)(148.5 k) +(1.5)(92.8 k) = 265.4 k ← controls.
LFRD ø = 0.75 ASD 𝛺 = 2.00
∅𝑅 𝑛 = (0.75)(265.4) = 199 k 𝑅 𝑛
𝛺
=
265.4
2.00
= 132.7 k.
Example: A connection of the type Fig. 1. must resist a service dead load of 9 kips and a
service live load of 18 kips. What total length of 1⁄4-inch fillet weld, E70XX electrode, is
required? Assume that both connected parts are 3⁄8 inch thick.
Fig.1.
LFRD Sol: Pu = 1.2D + 1.6L = 1.2(9) + 1.6(18) = 39.6 kips
The shear strength of the weld per inch of length is: 1.392D = 1.392(4) = 5.568 kips in.
The shear yield strength of the base metal is

53. 53 | P a g e
0.6 𝐹𝑦 𝑡 = 0.6(36)(
3
8
) = 8.1 kips/in.
and the shear rupture strength of the base metal is
0.45 𝐹𝑦 𝑡 = 0.45(58)(
3
8
) = 9.788 kips/in.
The weld strength of 5.568 kips in. governs. The total length required is:
39.6 𝑘𝑖𝑝𝑠
5.568 𝑘𝑖𝑝𝑠/𝑖𝑛.
= 7.11 in.
ASD Sol: Use 8 inches total, 4 inches on each side. Pa = D + L = 9 + 18 = 27 kips
The shear strength of the weld per inch of length is
0.9279D = 0.9279(4) = 3.712 kip sin.
The allowable shear yield strength of the base metal is
0.4 𝐹𝑦 𝑡 = 0.4(36)(
3
8
) = 5.4 kips/in.
and the allowable shear rupture strength of the base metal is
0.3 𝐹𝑦 𝑡 = 0.3(58)(
3
8
) = 6.525 kips/in.
The weld strength of 3.712 kips in. governs. The total length required is
27 𝑘𝑖𝑝𝑠
3.712 𝑘𝑖𝑝𝑠/𝑖𝑛.
= 7.27 in.
Use 8 inches total, 4 inches on each side.
Example: Select a 30 ft. long W-section of A36 steel to support a tensile service dead load of
140 kips and a tensile service load of 80 kips. The member will have two lines of bolts in each
flange (at least 3 bolts in a line). The bolts are 7/8” in dia.
Sol: Dead load = 140 kips. Live load = 80 kips. R = Lx = S = W = E = 0.
According to six Eq. (1): 𝐴 𝑢−1 = Pu = 1.4 D = 1.4 x 140 ⇒ Pu = 196 kips.
𝐴 𝑢−2 = Pu = 1.2D + 1.6L = 1.2 x 140 + 1.6 x 80 ⇒ Pu = 296 kips.
𝐴 𝑢−3 = Pu = 1.2D + 1.6L (Lr or S or R) + 0.5L or 0.8W
⇒ Pu = 1.2 x 140 + 1.6(0) + 0.5(80) ⇒ Pu = 208 kips.
𝐴 𝑢−4 = Pu = 0.9D – (1.3W or 1.5E) ⇒ Pu = 0.9 x 140 - (1.3 x 0) ⇒ Pu = 120 kips.
𝐴 𝑢−5 = Pu = 1.2D + 1.5E + 0.5L or 0.2S
⇒ Pu = 1.2 x 140 + 1.5(0) + 0.5(80) or 0.2 x 0 ⇒ Pu = 208 kips.
So, Required/critical load = 296 kips.
Now, ⇒ Minimum 𝐴 𝑔 =
𝑃𝑣
∅𝐹𝑦
=
296
0.9×36
= 9.14 in2.
⇒ Minimum 𝐴 𝑔 =
𝑃𝑣
∅ 𝑡 × 𝐹 𝑢 × 𝑈
+ Estimated hole area. But we need hole area first.
So hole size =
7
8
+
1
8
= 1”. ⇒ hole area = hole dia x thickness of flange
Assumption: Let we have to use W12 section having flange thickness approximately 0.52 inches
and also Assume that U = 0.85. so putting in Eq. i.e.,
𝐴 𝑔 =
296
0.85 × 58 × 0.75
+ 4 x 1 x 0.52 ⇒ 𝐴 𝑔 = 10.085 in2.

54. 54 | P a g e
Required minimum 𝐴 𝑔 of section = 10.1 in2. From manual use W12 x 36 section properties.
Properties of W12 x 36 section.
Area = 10.6 in2. Depth = d = 12 in. Breadth of flange = 𝑏𝑓 = 6.565 in.
Thickness of flange 𝑡𝑓 = 0.54. thickness of web two = 0.305. Radius of 𝑓𝑦 x Ϫ𝑡𝑖𝑜𝑛
About, x-Axis = Ϫ = 𝑟𝑥 = 5.15. About, y-axis = Ϫ = 𝑟𝑦 = 1.55.
Check: (i): 𝑀 𝑑 = ∅ 𝑡 𝑃𝑦 𝐴 𝑔 = 0.9 x 36 x 10.6. ⇒ 𝑀 𝑑 = 343.5 k > 296.
(ii): 𝑀 𝑑 = ∅ 𝑡 𝐹𝑣 𝐴 𝑒. For U we have 3 criteria.
(i): 𝑀 𝑑 ≤
2
3
𝑑 ⇒ 6.656 <
2
3
𝑑 ⇒ 𝜃 x
2
3
x 12 = 8. (ii): At least three rivet per line then V = 0.9.
𝐴 𝑛 = 𝐴 𝑔 − ∑ ℎ𝑜𝑙𝑒 𝑎𝑟𝑒𝑎 = 10.6 – 4 x 1 x 0.54 = 8.44. by putting values
𝑀 𝑑 = 0.75 × 𝐹𝑢 × 𝑈𝐴𝑣 × (𝐴 𝑛) ⇒ 𝑀 𝑑 = 0.75 × 58 × 0.9 × 8.44 ⇒ 𝑀 𝑑 = 330.5 > 296.
(ii):
𝐿
𝑟 𝑥
=
30×12
5.15
= 70 < 300.
𝐿
𝑟 𝑦
=
30×12
1.55
= 232.25 < 300.
It’s safe from buckling.
Example: Find net critical area for W12 x 16 section (𝑨 𝒈 = 4.71 in2.) connecting as shown.
Holes for inch bolts.
Sol: For path ABDE: ⇒ 𝐴 𝑛 = 𝐴 𝑔 – 2 x hole area ⇒ = 4.71 – 2 x
9
8
x 0.22. ⇒ 𝐴 𝑛 = 4.21 in2.
For path ABCDE: ⇒ 𝐴 𝑛 = 𝐴 𝑔 – 3 x hole area + 2 x
𝑆2
4𝐺
× 𝑡 𝑤
⇒ = 4.71 – 3 x
9
8
x 0.22 + 2 x
22
4×3
x 0.22. ⇒ 𝐴 𝑛 = 4.11 in2.
Example: Find the critical net area for a ½ in thick plate as shown in figure. The holes punched
by ¾ bolts.
Sol: Given: S = 3”. G = 3”. T =
1
2
”. B = 11”. Hole size = ¾ + 1/8 = 7/8.
Possible paths: 1: GEF cannot be critical as there is 1 hole.
2: ABCD: 𝐴 𝑛 = 𝐴 𝑔 – 2 x hole area ⇒ 11 x
1
2
- 2 x
7
8
x
1
2
= 4.6 in2.

55. 55 | P a g e
ABEF: ⇒ 𝐴 𝑛 = 𝐴 𝑔 – 2 x hole area + 1 x
𝑆2
4𝐺
× 𝑡
⇒ = 11 x
1
2
- 2 x
7
8
x
1
2
+ 1 x
32
4×3
x
1
2
. ⇒ 𝐴 𝑛 = 4.97 or 5 in2.
ABCEF: 𝐴 𝑛 = 𝐴 𝑔 – 3 x hole area + 1 x
𝑆2
4𝐺
× 𝑡
⇒ = 11 x
1
2
- 3 x
7
8
x
1
2
+ 1 x
32
4×3
x
1
2
. ⇒ 𝐴 𝑛 = 4.56 in2.
So the critical area = 4.56 in2.
Example: Find design tensile strength for W10 x 49 section whose flanges are welded at
support without any holes, however away from the end support holes are made as shown
along with welds the holes are 1” bolts, Using steel A36 and Fu = 58 ksi.
Sol: (1) At ends, only flanges are welded without any holes.
𝐴 𝑒 = Area of directly connected parts = Area of two flanges.
So, 𝐴 𝑒 = 𝜃 x 10 x 0.56 ⇒ 𝐴 𝑒 = 11.2 in2. ⇒ 𝜃 = 2.
(ii): Away from ends support, holes are also made along with welds.
𝐴 𝑒 = 𝐴 𝑛 = 𝐴 𝑔 − ∑ ℎ𝑜𝑙𝑒𝑠 𝑎𝑟𝑒𝑎 ⇒ hole size = 1 +
1
8
=
9
8
".
𝐴 𝑛 = 14.4 – 4 x
9
8
x 0.56 ⇒ 𝐴 𝑛 11.38.
Now 𝑃𝑑 = 0.9𝐹𝑦 × 𝐴 𝑔 ⇒ 0.9 x 36 x 14.4 ⇒ = 467 kips.
𝑃𝑑 = 0.9𝐹𝑢 × 𝐴 𝑒 ⇒ 0.75 x 58 x 11.32 ⇒ = 495 kips.
Example 7.1. Two plates 16 mm thick are joined by i. a double U butt weld, ii. A single U butt
weld. Determine the strength of the welded joint in tension in each case. Effective length of
weld is 150 mm. Allowable stress in butt weld in tension is 142 N/mm2.
Solution: i. In case of double U but weld, complete penetration of weld takes place
Effective throat thickness of weld = 16 mm. Effective length of weld = 150 mm.
Strength of single U butt weld = throat thickness x length of weld x permissible shear stress
= (16 x 150 x 142/1000) = 340.8 Kn.
ii. In case of single U butt weld, incomplete penetration of butt weld takes place
Effective throat thickness = 5/8 x 16 = 10 mm. Effective length of weld = 150 mm
Strength of single U butt weld = (10 x 150 x 142/1000) = 213.0 Kn.
Example 7.2. In a truss girder of a bridge, a tie as shown in Fig. 7.18 is connected to the
gusset plate by fillet weld. Determine the strength of the weld. The size of the weld in the
fillet weld is 6 mm.

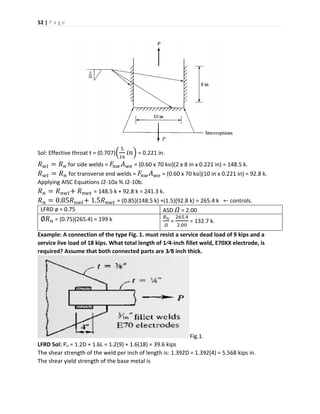
56. 56 | P a g e
Sol: Size of weld = 6 mm
Effective throat thickness = 0.7 x 6 = 4.2 mm
Effective length of fillet weld
= 200 + 200 + 200 = 600 mm
Strength of fillet weld
= (4.2 x 600 x 110/1000) = 277.2 KN.
Example 7.3. In Example 7.2, the pull to be transmitted by the tie is 300 KN. Determine the
necessary overlap of the tie.
Solution: Size of weld = 6 mm
Effective throat thickness = 4.2 mm
Pull transmitted by the end fillet weld = (4.2 x 200 x 110/1000) = 92.4 kN
Let l be the necessary overlap required, the pull transmitted by the side fillet is
= (4.2 x 2 x l x 110/1000) = 0.924 l KN.
Total pull transmitted = 92.4 + 0.924 l = 300 KN.
Therefore, the necessary overlap of the tie l = 224.7 mm.
Example 7.4. The web plate of a built-up welded I-section is 200 mm x 12 mm and the flange
plates are 100 mm x 12 mm. The size of fillet weld is 6 mm. Compute the maximum shear
force that may be allowed at any section, if the average allowable shear in the web is 0.4
fy and maximum allowable shear in the weld is 110 N/mm2.
Solution: Moment of inertia of the built-up section (about xx axis)
𝐼𝑥𝑥 = 1/12[10 x 22.43 – 8.8 x 203] x 104 = 3499.52 x 104 mm4.
Intensity of shear stress (at weld section): 𝜏 𝑠 = (
𝐹.𝐴𝑦̅
𝐼 𝑥𝑥.(2𝑡)
)
Where,
𝐴𝑦̅ = Moment of the area above the section about xx axis.
F = shear force at the section.
t = Effective throat thickness of one weld.
𝜏 𝑠 = (
𝐹×100×12×(100+6)
3499.52×104×2×0.7×6
)
= 0.11 KN/mm2. F = 254.21 KN.
The average shear stress in the web is 0.4 x 250 N/mm2.
Allowable shear force in the web:
F1 = (200 x 12 x 0.4 x 250/1000) = 240 KN.
The design drawing is Fig. 7.19.
Example 7.5. Design a suitable longitudinal fillet weld to
connect the plates as shown in Fig. 7.20 and to transmit a pull equal to the full strength of

57. 57 | P a g e
thin plate. Allowable stress in the weld is 110 N/mm2 and tensile stress in the plate 0.6
fy N/mm2. The plates are 10 mm thick.
Solution: The minimum size of weld
required for thickness up to 20 mm
is 5 mm. The maximum size of fillet
weld is limited by the thickness of
the plate is (10 - 1.5) = 8.5 mm.
Provide 6 mm fillet weld.
Pull transmitted by 1 mm weld
= (1 x 0.7 x 6 x 110/1000) = 0.462 KN.
Tensile strength of thin plate = (120 x 10 x 0.6 x 250/1000) = 180 KN.
Necessary length of the weld = (180 / 0.462) = 389.61 mm.
Provide 195 mm longitudinal weld on each side. Check: Length of the weld 195 mm is greater
than perpendicular distance 120 mm between welds.
Example 7.6. Two plates 120 mm x 10 mm are overlapped and connected together by
transverse fillet weld to transmit pull equal to full strength of the plate. Design the suitable
welding. Allowable stress in the weld is 110 N/mm2. Allowable stress in tension in the plate is
0.6 fy N/mm2.
Solution: Minimum size of weld = 5mm. Maximum size of weld = (10-1.5) = 8.5 mm
Total length of two welds = 240 mm
Total load transmitted by 6 mm weld = (240 x 0.7 x 6 x 110/1000) = 110.88 KN.
Maximum pull that can be transmitted by the plate = (120 x 10 x 0.6 x 250/1000) =180 KN.
To transmit the pull equal to the full strength of plate, provide additional weld by plug weld.
Provide two rectangular plug welds 30 mm x 15 mm as shown in Fig. 7.21 which satisfies the
specification.
Strength of two plug welds
= (2 x 30 x 15 x 110/1000) = 99 KN.
Total pull now transmitted
= (110.88 + 99)
= 209.88 KN > 180 KN.
Hence satisfactory.
Example 7.7. A tie member consists of two MC 225, @ 0.250 kN/m. The channels are
connected to either side of a gusset plate 12 mm thick. Design the welded joint to develop
the full strength of the tie. The overlap limited to 400 mm.
Solution: From ISI Handbook No. 1, for MC 225, @ 0.250 kN/m

58. 58 | P a g e
Thickness of web = 6.4 mm. Thickness of flange = 12.4 mm. Sectional area = 3301 mm2.
Tensile strength of each channel section = (3301 x 0.6 x 250/1000) = 495.15 kN
Provide 4 mm weld. Strength of weld per mm length = (1 x 0.7 x 4 x 110/1000) = 0.308 kN
Total length of fillet welds necessary to connect one channel section = (
495.15
0.308
) = 1607.6 mm.
The overlap of channel is limited to 400 mm. the width of slot should not be less than 3 times
thickness (3 x 6.4 = 19.2 mm). Provide two slots 20 mm side. The distance between edge of the
slot and edge of channel or between adjacent slots also should not be less than twice the
thickness (2 x 6.4 = 12.8 mm). Provide these distances as shown in Fig. 7.22. Let x be the length
of the slot. The total length of the weld = 800 + 225 + 4x – 2 x 20 = 1607.6 mm
Therefore, the length of the slot x = 155.65 mm ≈ 160 mm long fillet welding is done as shown
in Fig. 7.22.
Example: Design the size and length of Fillet weld for the lap joint shown below,
Use SMAW E 70XX process, plates are A-36 steel ?
Solution: Factored load = 1.2 x 25 + 1.6 x 70 = 142 kips.
Minimum weld size = ¼ inch (AISC table J 2.4). Maximum weld size =
5
8
−
1
16
=
9
16
(AISC 2 – 2b).
Select size (5/16 inch) since you can get it in a single pass. te = 0.707 x 5/16 = 0.22 inch.
1) Weld capacity per inch = Rnw = 0.75 te (0.6 FEXX)
= 0.75 x 0.22 x 0.6 x 70 = 6.96 kips per inch (controls).
2) Plate shear-rupture = Rnw = t (0.6Fu) = 0.75 x 0.625 x 0.6 x 58 = 16.3 kips per inch.

59. 59 | P a g e
3) Total length of weld required: 𝐿 𝑤 =
𝑃 𝑢
∅𝑅 𝑛𝑤
=
142
6.90
= 20.4 inches.
Use weld around plate as shown in Fig. (Use three sides of 7 inch each = 21 inch).
Example: An ISA 90  90  8 used as tension member is connected to a 10 mm gusset plate by
fillet weld of size 5 mm. The design strength of the member is 300 KN. Calculate the length of
the weld. (a) lower side 324 mm and upper side 125 mm
Solution: Force resisted by weld at lower side of angle P1 = 300 ×
90−25.1
90
= 216.33 KN.
Force resisted by weld at upper side of angle P2 = 300 ×
25.1
90
= 83.67 KN.
Assuming size of weld as 5mm, the throat thickness te will be 0.707 × 5 = 3.535 mm
Length required at lower side: 𝐿 𝑤1 =
𝑃1
𝑡 𝑒 𝑓 𝑢
√3𝛾 𝑚𝑤
=
216.33×103
3.535×410
√3×1.25
= 323.15 mm ≈ 324 mm.
Length required at upper side: 𝐿 𝑤2 =
𝑃2
𝑡 𝑒 𝑓 𝑢
√3𝛾 𝑚𝑤
=
83.67×103
3.535×410
√3×1.25
= 124.9 mm ≈ 125 mm.
Example: Determine the design strength of the connection system shown below. The tension
member is a 4 in. x 3/8 in. thick rectangular bar. It is welded to a 1/2 in. thick gusset plate
using E70XX electrode.
Solution: step 1: Check limitations on the weld geometry: tmin = 3/ 8" (Member). tmax = 0.5"
(gusset plate). Thus from Table J2.4 of AISC with tmin = 3/ 8" thus: wmin 3 /16 in. For tmax = 0.5.
wmax = t - 1 /16 = 0.5 - 1 /16 = 7 /16 in. Fillet weld size = w = 1/4 in.
𝑤 𝑚𝑖𝑛 < 𝑤 = 1/4" < 𝑤 𝑚𝑎𝑥 → 𝑜𝑘 ⇒ 𝐿 = 5" > 4𝑤 = 4 × 0.25 = 1.0 → 𝑜𝑘
L =5" > transverse distance between welds = 4 " OK.
𝐿
𝑤
=
5
0.25
= 20 < 100 → 𝐿 𝑒𝑓𝑓 = L → ok.
Step II : Design strength of the weld
 Weld strength: Fw = 0.6FEXX = 0.6 x 70 = 42 ksi.
∅𝑅 𝑛 = 0.75 x Fw x 0.707 x w x L = 0.75 x 42 x 0.707 x 0.25 x 10 = 55.67 kips.
 Base metal length: ∅𝑅 𝑛 = min {1.0(0.6 Fy tL), 0.75(0.6 Fu tL)}

60. 60 | P a g e
∅𝑅 𝑛 = min {
1.0(0.6 × 50 × 10 × 3/8
0.75(0.6 × 65 × 3/8 × 10
} ⇒ ∅𝑅 𝑛 = min{112.5, 109.69} = 109.69 kips.Thus weld strength control and the connection strength = 55.67 kips
EXAMPLE: A compression member is subjected to service loads of 165 kips dead load and 535
kips of live load. The member is 26 ft. long and pinned at each end. Use A992 (50 ksi) steel
and select a W shape.
Solution: • Calculate the factored design load Pu
Pu = 1.2 PD + 1.6 PL = 1.2 x 165 + 1.6 x 535 = 1054 kips
Select a W shape from the AISC manual Tables
For KyLy = 26 ft. and required strength = 1054 kips
Select W14 x 145. It has φcPn = 1160 kips. Select W12 x 170. It has φcPn = 1070 kips
No W10 will work. W14 x 145 is the lightest
Note that column sections are usually W12 or W14. Usually sections bigger than W14 are
usually not used as columns.
Example: The rigid frame shown below is unbraced. each member is oriented so that its web
is in the plane of frame. Determine the effective length factor Kx for columns AB and BC.
Solution: Column AB:
For joint A, 𝐺 =
𝛴𝐼 𝑐/𝐼 𝑐
𝛴𝐼 𝑔/𝐼 𝑔
=
833/12 + 1070/12
1360/20 +1830/18
=
1586
1697
= 0.93.
For joint B, 𝐺 =
𝛴𝐼 𝑐/𝐼 𝑐
𝛴𝐼 𝑔/𝐼 𝑔
=
1070/12 + 1070/12
169.7
=
160.5
169.7
= 0.95.
From the alignment chart for sides way uninhibited (AISC Fig. C-C2.2b), with GA = 0.93 and GB =
0.95, Kx = 1.31 for column AB. For column BC: For joint B, as before, G = 0.95.
For joint C. a pin connection. the situation is analogous to that of a very stiff column attached to
infinitely flexible girders - that is. girders of zero stiffness. The ratio of column stiffness to girder
stiffness would therefore be infinite for a perfectly frictionless hinge. This end condition can

61. 61 | P a g e
only be approximated in practice, so the discussion accompanying the alignment chart
recommends that G be taken as 10.0.
From the alignment chart with GA = 0.95 and GB = 10.0, Kx = 1.85 for column BC.
EXAMPLE: Select the lightest W-shape that can resists a factored compressive load Pu of
190 kips. The effective length is 24 feet. Use ASTM A572 Grade 50 steel.
SOL: The appropriate strategy here is to find the lightest shape for each nominal size and then
choose the lightest overall. The choices are as follows.
W4, W5 and W6: None of the tabulated shape will work.
W8: W 8  58, cPn = 205 kips. W10: W10  49, cPn = 254 kips
W12: W12  53, cPn = 261 kips. W14: W14  61, cPn = 293 kips
Note that the load capacity is not proportional to the weight (or cross-sectional area). Although
the W8  58 has the smallest design strength of the four choices, it is the second heaviest.
ANSWER: Use a W10  49.
Example: Select a W18 shape of A36 steel that can resist a factored load of 1054 kips.
The effective length KL is 26 feet.
Sol: Try Fcr = 24 ksi (two-thirds of Fy):
Required 𝐴 𝑔 =
𝑃 𝑢
∅ 𝑐 𝐹𝑐𝑟
=
1054
0.9(24)
= 48.8 in2. Try W18 x 192: 𝐴 𝑔 = 56.4 in2 > 48.8 in2.
𝐾𝐿
𝑟 𝑚𝑖𝑛
26(12)
2.79
= 111.8 < 200. (OK) ⇒ 𝐹 𝑒 =
𝜋2 𝐸
(
𝐾𝐿
𝑟
)
2 =
𝜋2×29000
(111.8)2 = 22.9 ksi.
𝐹𝑒 > 0.44 𝐹𝑦 (15.84). LFRD Eq. E.3.2.
𝐹𝑐𝑟 = [0.658
𝐹 𝑦
𝐹 𝑒 ] 𝐹𝑦 = [0.658
36
22.9] x 36 = 0.532 x 36 = 18.64 ksi.
∅ 𝑐 𝑃𝑛 = 0.9𝐴 𝑔 𝐹𝑐𝑟 = 0.9 x 56.4 x 18.64 = 943 kips < 1054k.
Try 𝐹𝑐𝑟 = 18.64 ksi ( the value just computed for the W18 x 192):
Required 𝐴 𝑔 =
𝑃 𝑢
∅ 𝑐 𝐹𝑐𝑟
=
1054
0.9(18.64)
= 62.83 in2. Try W18 x 234: 𝐴 𝑔 = 68.8 in2 > 62.83 in2.
𝐾𝐿
𝑟 𝑚𝑖𝑛
26(12)
2.85
= 109.5 < 200. (OK) ⇒ 𝐹 𝑒 =
𝜋2 𝐸
(
𝐾𝐿
𝑟
)
2 =
𝜋2×29000
(109.5)2 = 23.87 ksi.
𝐹𝑒 > 0.44 𝐹𝑦. LFRD Eq. E.3.2.
𝐹𝑐𝑟 = [0.658
𝐹 𝑦
𝐹 𝑒 ] 𝐹𝑦 = [0.658
36
23.87] x 36 = 0.532 x 36 = 19.15 ksi.
∅ 𝑐 𝑃𝑛 = 0.9𝐴 𝑔 𝐹𝑐𝑟 = 0.9 x 68.8 x 19.15 = 1185 kips < 1054k. (OK).
This shape is not in the column load tables, so the width thickness ratios must be checked.
𝑏 𝑓
2𝑡 𝑓
= 2.8 <
95
√36
= 15.8 (ok).
ℎ
𝑡 𝑤
= 13.8 <
253
√36
= 42.2 (ok). Use a W18 x 234. Ans.