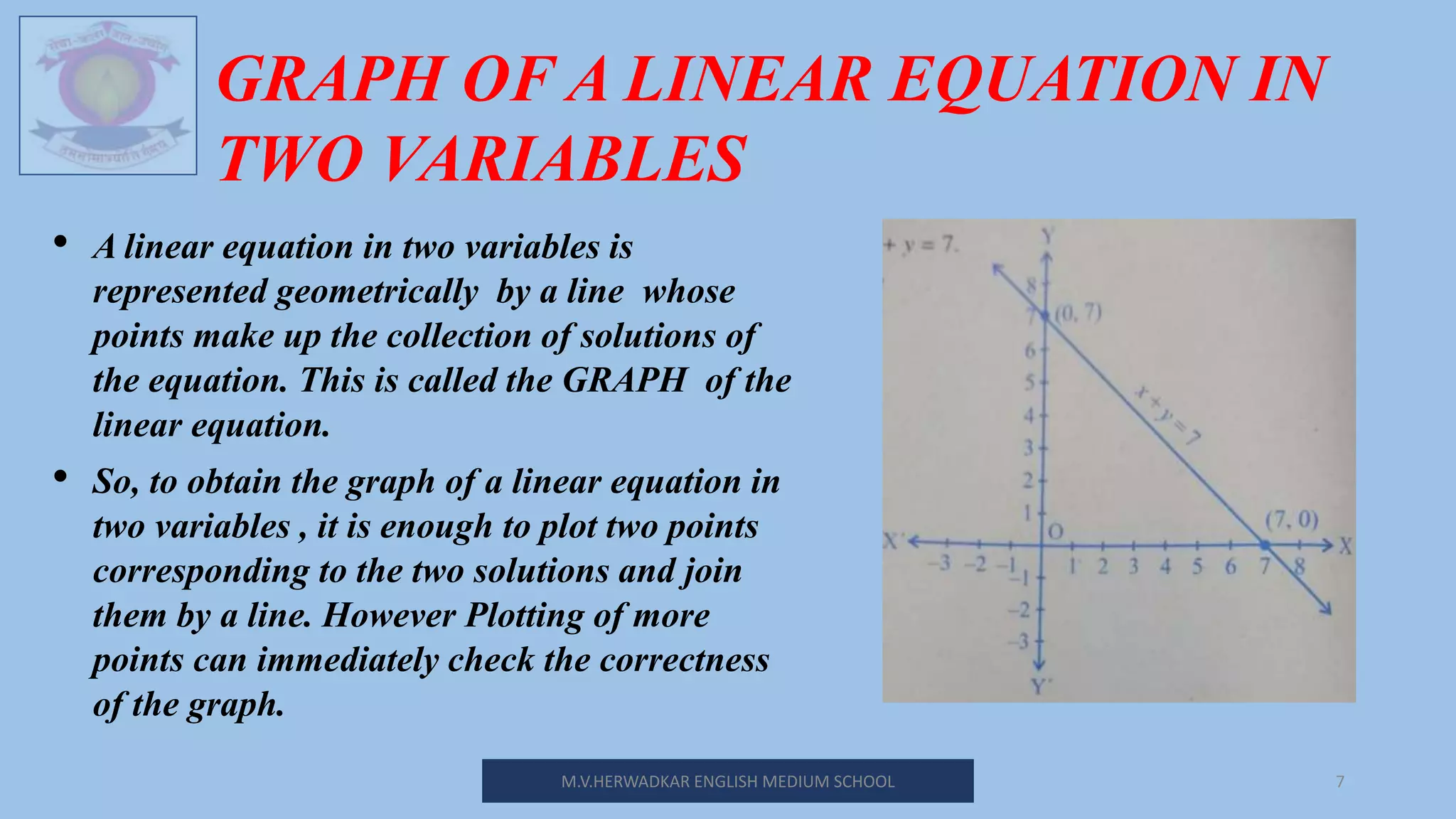
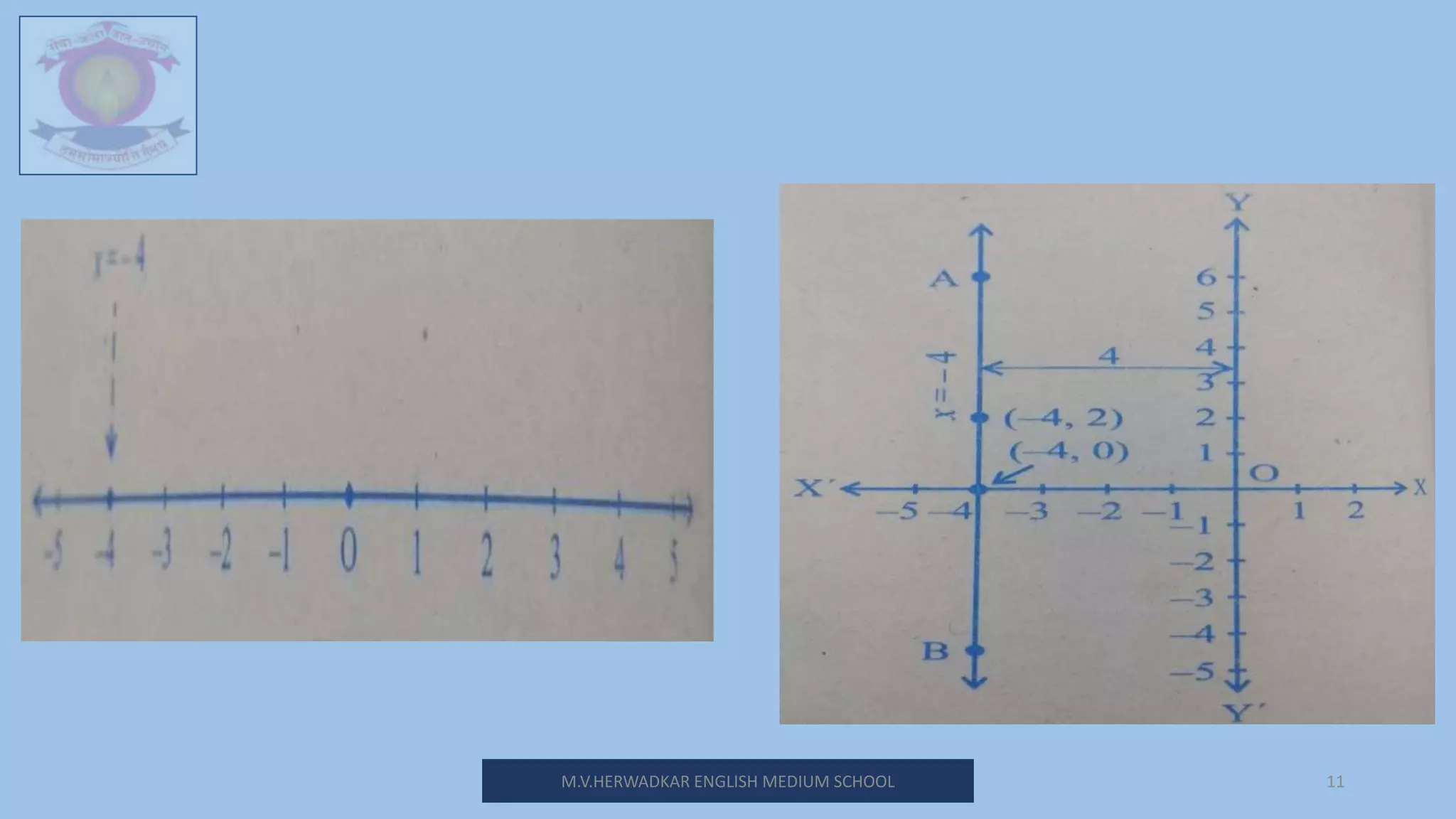
This document is a lesson plan on linear equations in two variables for a 9th grade class. It introduces linear equations, provides examples of linear equations in one and two variables, and discusses representing the solutions of linear equations on number lines and graphs. The lesson defines what makes an equation linear, explains that linear equations in two variables can have multiple solutions which are pairs of values, and shows how to graph linear equations by plotting points. It also discusses equations for lines parallel to the x and y axes. The lesson includes exercises for students to practice solving and graphing various linear equations in two variables.

1. B.J.P.S Samiti’s
M.V.HERWADKAR ENGLISH MEDIUM HIGH SCHOOL
CLASS 9th: LINEAR EQUATIONS IN TWO VARIABLES
Program:
Semester:
Course: NAME OF THE COURSE
Staff Name: VINAYAK PATIL 1

2. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 2
• All of you have studied about linear equations in earlier classes.
• x + 1 = 0 , x -3 = 0 , y - √2 = 0 , √2 y + √3 = 0
are examples of linear equations in one variable . These have unique
solution and all of you know how to represent solution of linear
equation on number line.
Here, in this chapter , we will extend your knowledge of linear
equation in one variable into linear equation of two variables.
INTRODUCTION

3. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 3
LINEAR EQUATION
A linear equation is an algebraic
equation in which each term is
either a constant or the product of a
constant and a single variable.
Linear equations can have one or
more variables.
X + 2 = 0
X = -2
-3 -2 -1 0 1 2 3

4. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 4
EXERCISE 10.1
• 1) The cost of a notebook is twice the cost of the pen write a linear
equation in two variables to represent this statement?

5. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 5
SOLUTIONS OF A LINEAR EQUATIONS
Every linear equation has a unique solution
as there is a single variable in the equation to
be solved but in a linear equation involving
two variables in the equation, a solution
means a pair of values, one for x and one for
y which satisfy the given equation

6. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 6
EXERCISE 10.2
1) Find four solutions of the equations:
(i)2x + y = 7 , (ii) x = 4y .
2) Find the value of k , if x = 2 and y = 1 is the
solution of the equation 2 x + 3 y = k

7. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 7
GRAPH OF A LINEAR EQUATION IN
TWO VARIABLES
• A linear equation in two variables is
represented geometrically by a line whose
points make up the collection of solutions of
the equation. This is called the GRAPH of the
linear equation.
• So, to obtain the graph of a linear equation in
two variables , it is enough to plot two points
corresponding to the two solutions and join
them by a line. However Plotting of more
points can immediately check the correctness
of the graph.

8. EXERCISE 10.3
1) Draw the graph of i) x + y = 4 ii) y = 3x
M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 8

9. Equations of Lines Parallel to the x-axis
and y-axis
• Well students , all of you know that the points (2,0) ,
(-3,0 ) , (4,0) , (n,0) ,for any real number n , lie in the
Cartesian plane ,even they all lie on x-axis. Because
on the x-axis , the ycoordinate of each point is zero.
In fact , every point on the x-axis is of the form (x,0).
SO, the equation of x-axis is y = 0 which can be
expressed as 0.x + 1.y = 0
• Similarly , equation of y- axis is given by x = 0
M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 9

10. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 10
1) Solve the equation 2x + 1 = x – 3 and
represent the solution(s) on
(i) number line (ii) the cartesian plane .
Sol. 2 x + 1 = x – 3 gives us 2x – x = -3 – 1
i.e. x = - 4

11. M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 11

12. EXERCISE 10.4
M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 12
Give the geometric representations of
2 x + 9 = 0 as an equation
(i) in one variable
(ii) in two varaibles.

13. HOMEWORK
1) Define linear equation in two variables with
example
M.V.HERWADKAR ENGLISH MEDIUM SCHOOL 13