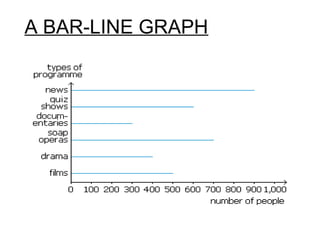
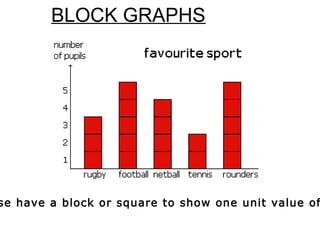
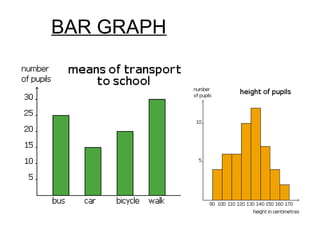
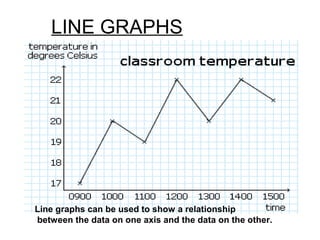
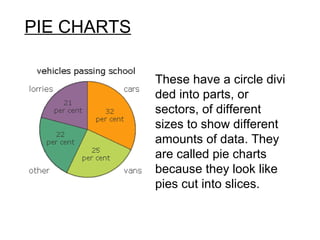
This document provides an overview of statistics as a branch of mathematics dealing with the collection, organization, and analysis of numerical data to aid decision making. It discusses the history of basic statistical methods dating back to ancient civilizations, and outlines common statistical methods like collecting primary and secondary data, tabulating and presenting data, calculating measures of central tendency and variability, using graphs to visualize data, and determining correlation between variables. The goal of statistics is to accurately represent large data sets and analyze relationships within the data.

1. STATISTICS
MRS.P.NAYAK,P.G.T K.V.F.W

2. STATISTICS
Statistics, branch of mathematics
that deals with the collection,
organization, and analysis of
numerical decision-making.

3. HISTORY
Simple forms of statistics have
been used since the beginning of
civilization, when pictorial
representations or other symbols
were used to record numbers of
people, animals, and inanimate
objects on skins, slabs, sticks of
wood, or the walls of caves.

4. Before 3000 bc the
Babylonians used small
clay tablets to record
tabulations of agricultural
yields and of commodities
bartered or sold.

5. The Egyptians analysed the
population and material wealth of
their country before beginning to
build the pyramids in the 31st century
bc.

6. The Roman Empire was the first
government to gather extensive data
about the population, area, and
wealth of the territories that it
controlled.

7. Registration of deaths and births was
begun in England in the early 16th
century, and in 1662 the first
noteworthy statistical study of
population.

8. At present, statistics is a reliable means
of describing accurately the values of
economic, political, social, psychological,
biological, and physical data and serves
as a tool to correlate and analyse such
data. The work of the statistician is no
longer confined to gathering and
tabulating data, but is chiefly a process of
interpreting the information.

9. STATISTICAL METHODS
STEPS
• COLLECTION OF DATA
• TABULATION AND PRESENTATION
OF DATA
• INTERPRETATION OF DATA.

10. COLLECTION OF DATA:
Primary Data –
When Data are collected directly
it is called Primary Data.
Secondary Data.
If they are collected through
others than it is called
Secondary Data.

11. TABULATION AND
PRESENTATION OF DATA
The collected data are called
RAW DATA

12. TABULATION AND
PRESENTATION OF DATA
1. They must be arranged either
ascending order or descending order.
2. They are grouped.
3. They are tabulated.
4. Construction of frequency distribution
table.(Grouped / Ungrouped)

13. INTERPRETATION OF
DATA.
(a) From graph
(b) Measures Of Central Tendency
(c) Measures Of Variability
(d) Measures Of Variability
(e) Co-relation
(f) Mathematical Models

14. GRAPHICAL REPRESENTATION OF DATA
(i) Pictorial graph
(ii) Bar Graph
(iii) Histogram
(iv) Frequency polygon

15. GRAPHS Graphs are used to display
number information, or data,
in a visual way that is easy to
understand and interpret.
They are usually drawn with
two lines, called axes, which
meet at a right angle like this.
The line going across the
page is the horizontal axis,
and the line going up the page
is the vertical axis. The axes
are labelled to show the type
of data and the value of the
data being shown

16. A BAR-LINE GRAPH

17. BLOCK GRAPHS
se have a block or square to show one unit value of

18. BAR GRAPH

19. LINE GRAPHS
Line graphs can be used to show a relationship
between the data on one axis and the data on the other.

20. PIE CHARTS
These have a circle divi
ded into parts, or
sectors, of different
sizes to show different
amounts of data. They
are called pie charts
because they look like
pies cut into slices.

21. MEASURES OF CENTRAL TENDENCY
After data have been collected and
tabulated, analysis begins with the
calculation of a single number, which will
summarize or represent all the data.
Because data often exhibit a cluster or
central point, this number is called a
measure of central tendency.
Mean
Median
Mode

22. MEASURES OF CENTRAL TENDENCY
Let x, x2, ..., xn be the numbers of some statistic. The
most frequently used measure is the simple arithmetic
average, or mean, written, which is the sum of the
numbers divided by n:

23. MEASURES OF CENTRAL TENDENCY
After data have been collected and tabulated, analysis
begins with the calculation of a single number, which
will summarize or represent all the data. Because data
often exhibit a cluster or central point, this number is
called a measure of central tendency.
Let x1, x2, ..., xn be the numbers of some statistic. The
most frequently used measure is the simple arithmetic
average, or mean, written , which is the sum of the
numbers divided by n:
The symbol Σ denotes the sum of all values. If the xs
are grouped into k intervals, with midpoints m1, m2, ...,
mk and frequencies f1, f2, ..., fk, respectively, the
simple arithmetic average is given by
with i = 1, 2, ..., k.

24. MEASURES OF CENTRAL TENDENCY
The median and the mode are two other measures of
central tendency. Let the xs be arranged in numerical
order; if n is odd, the median is the middle x; if n is
even, the median is the average of the two middle xs.
The mode is the x that occurs most frequently. If two or
more distinct xs occur with equal frequencies, but none
with greater frequency, the set of xs may be said not to
have a mode or to be bimodal, with modes at the two
most frequent xs, or trimodal, with modes at the three
most frequent

25. VARIABILITY OF THE DISTRIBUTION
The investigator is frequently concerned with the
variability of the distribution, that is, whether the
measurements are clustered tightly around the mean or
spread over the range. One measure of this variability is
the difference between two percentiles, usually the 25th
and the 75th percentiles. The pth percentile is a number
such that p per cent of the measurements are less than
or equal to it; in particular, the 25th and the 75th
percentiles are called the lower and upper quartiles,
respectively.

26. VARIABILITY OF THE DISTRIBUTION
The standard deviation is a measure of variability that is
more convenient to use than percentile differences as it
is defined via basic arithmetic terms as follows. The
simple deviation of a number in a set is defined as the
difference between that number and the mean of the
set. For example, in the series x1, x2, ..., xn, the
deviation of x1 is x1 - , and the square of the deviation
is (x1 - )2. The variance of the set is the mean of the
square deviations. Finally, the standard deviation,
denoted by σ (the lower-case Greek letter sigma), is the
square root of the variance, and is calculated as follows,

27. CORRELATION
When two social, physical, or biological phenomena
increase or decrease proportionately and
simultaneously because of identical external factors, the
phenomena are positively correlated; if one increases in
the same proportion that the other decreases, the two
phenomena are negatively correlated. Investigators
calculate the degree of correlation by applying a
coefficient of correlation to data concerning the two
phenomena. The most common correlation coefficient is
expressed as

28. CORRELATION
in which x is the deviation of one variable from its mean,
y is the deviation of the other variable from its mean,
and N is the total number of cases in the series. A
perfect positive correlation between the two variables
results in a coefficient of +1, a perfect negative
correlation in a coefficient of -1, and a total absence of
correlation in a coefficient of 0. Thus, .89 indicates high
positive correlation, -.76 high negative correlation, and .
13 low positive correlation.

29. A MATHEMATICAL MODEL
In a related but more involved example of a
mathematical model, many sets of measurements have
been found to have the same type of frequency
distribution—for example, the number of 6s cast in runs
of n tosses of a die; the weights of N beans chosen
haphazardly from a bag; the barometric pressures
recorded by different students, reading the same
barometer.