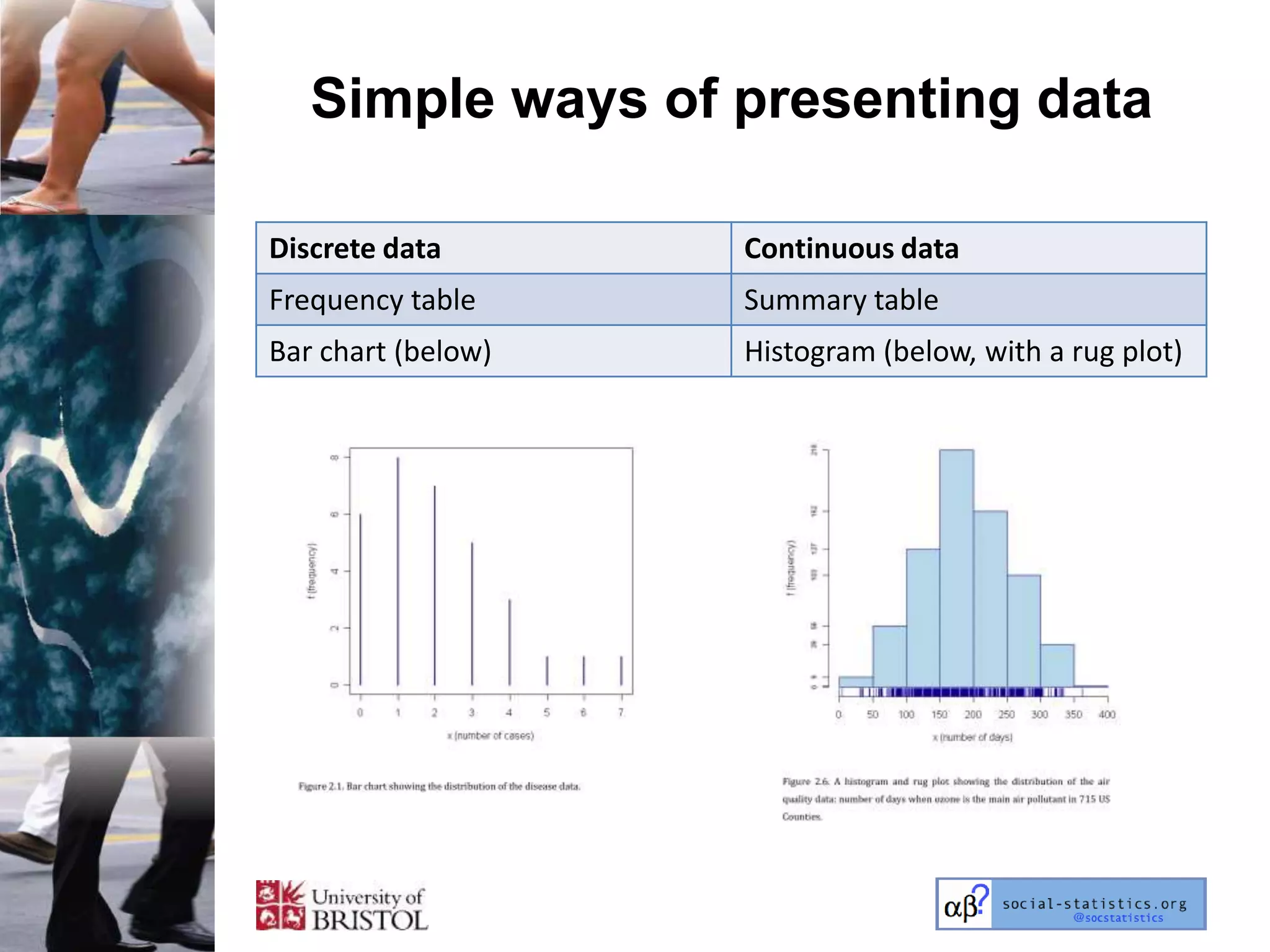
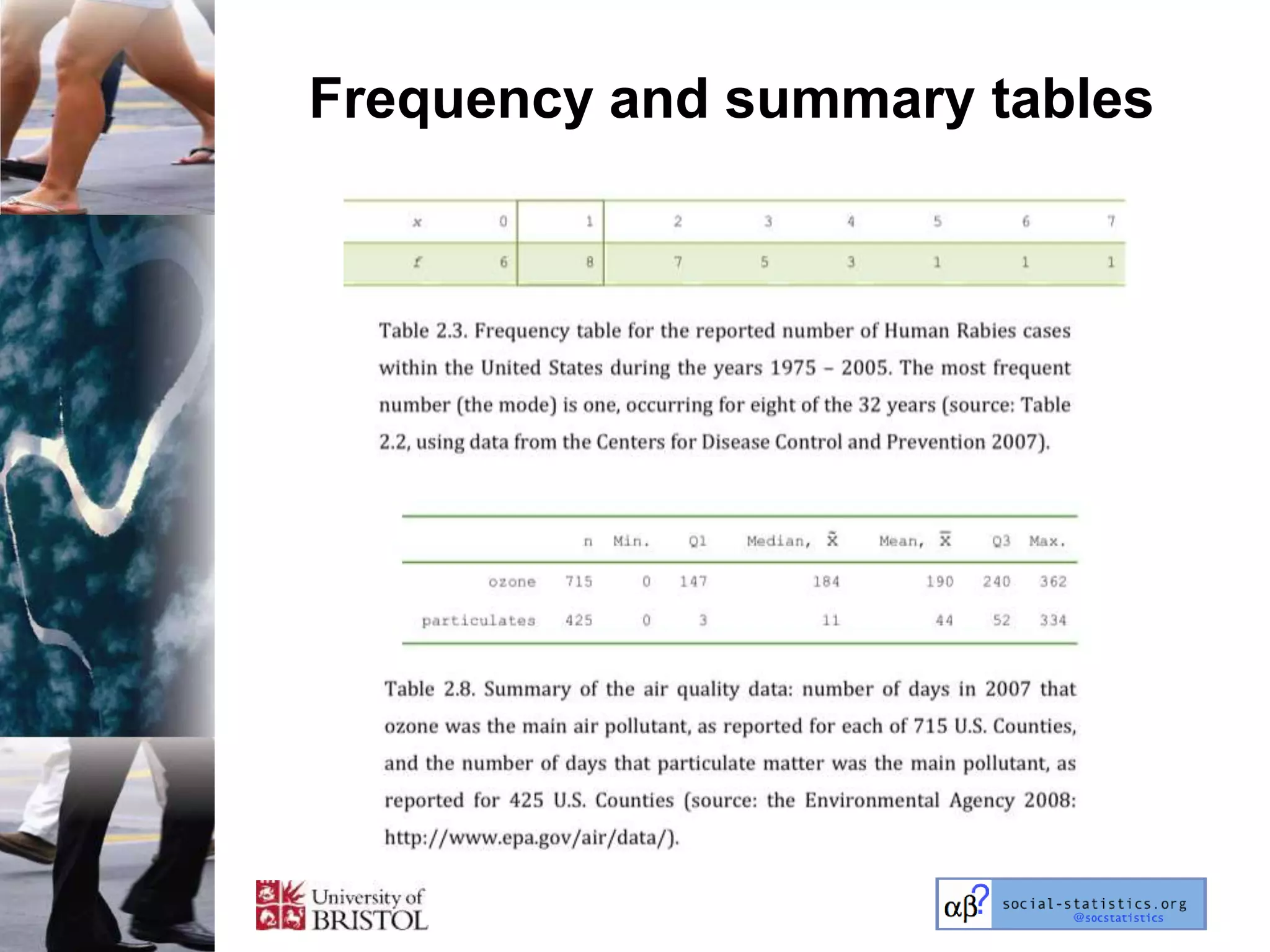
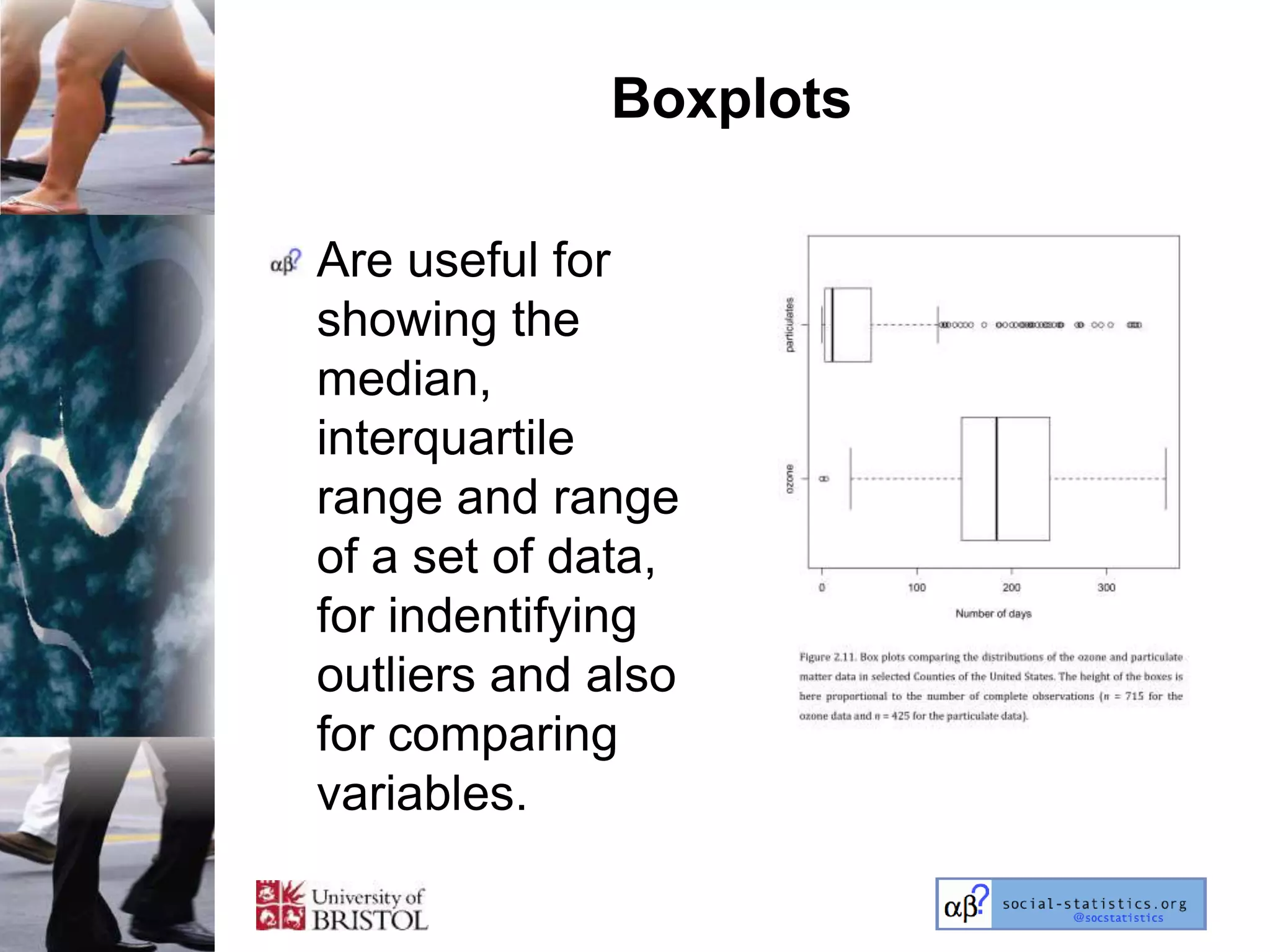
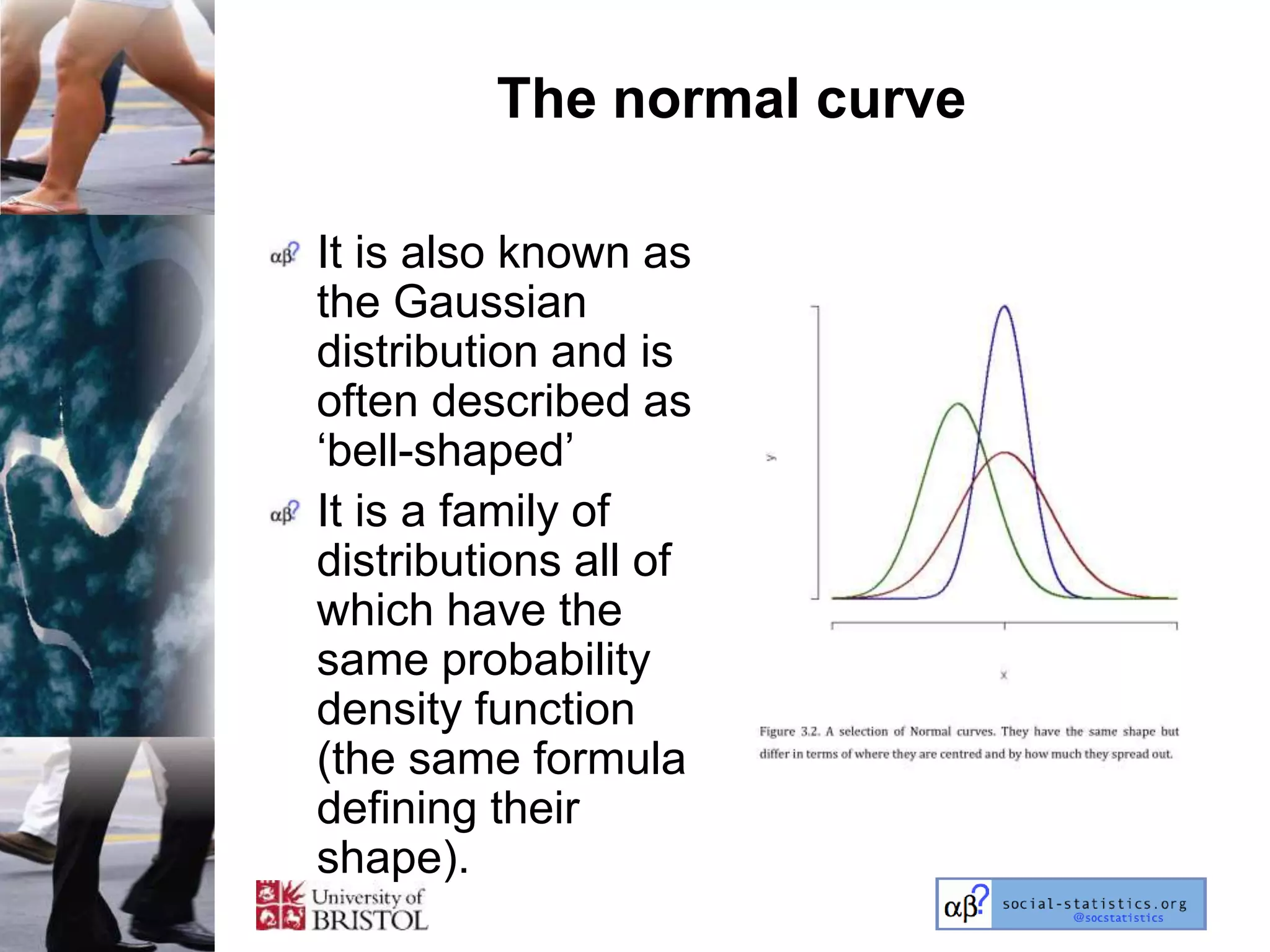
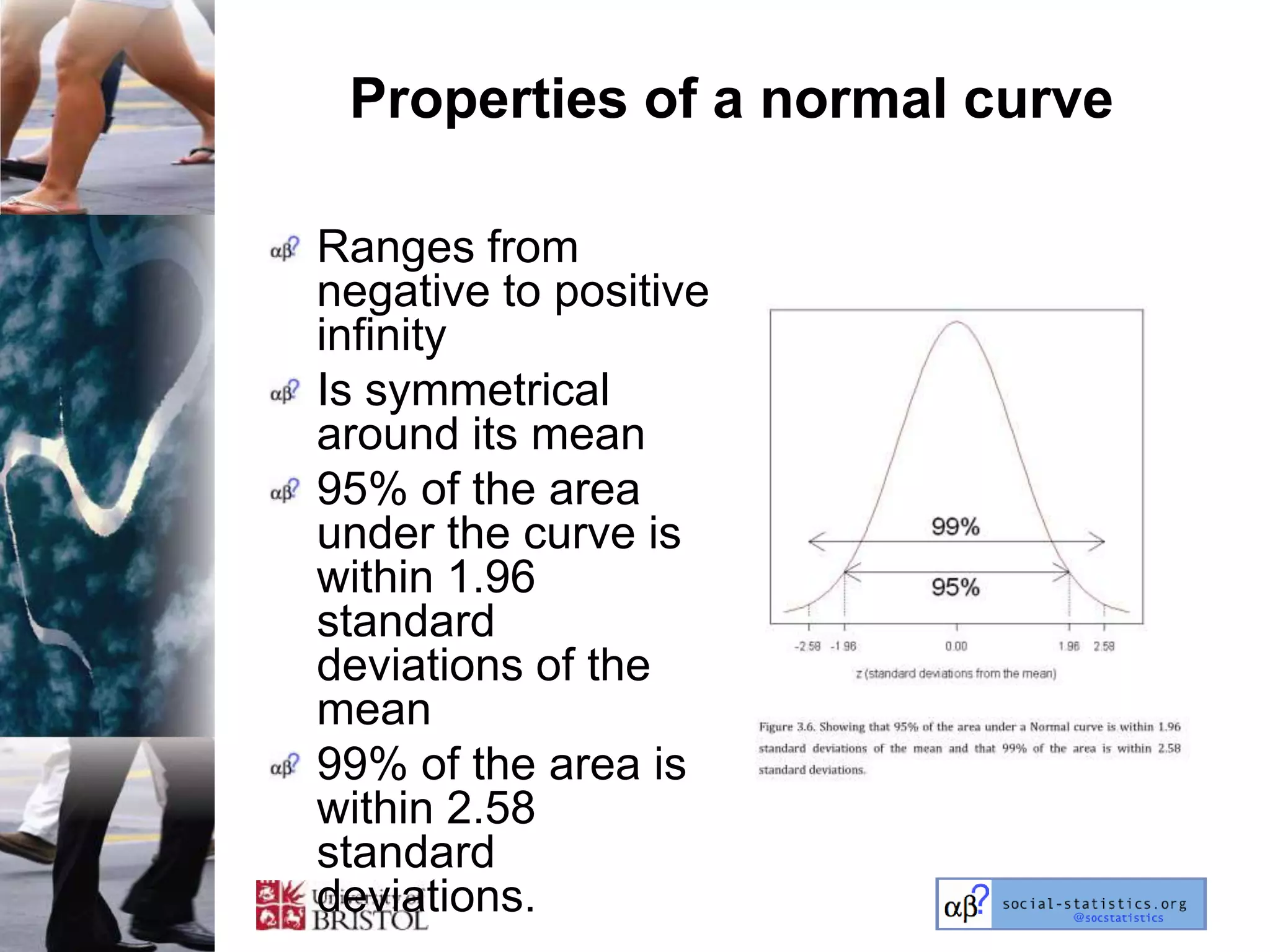
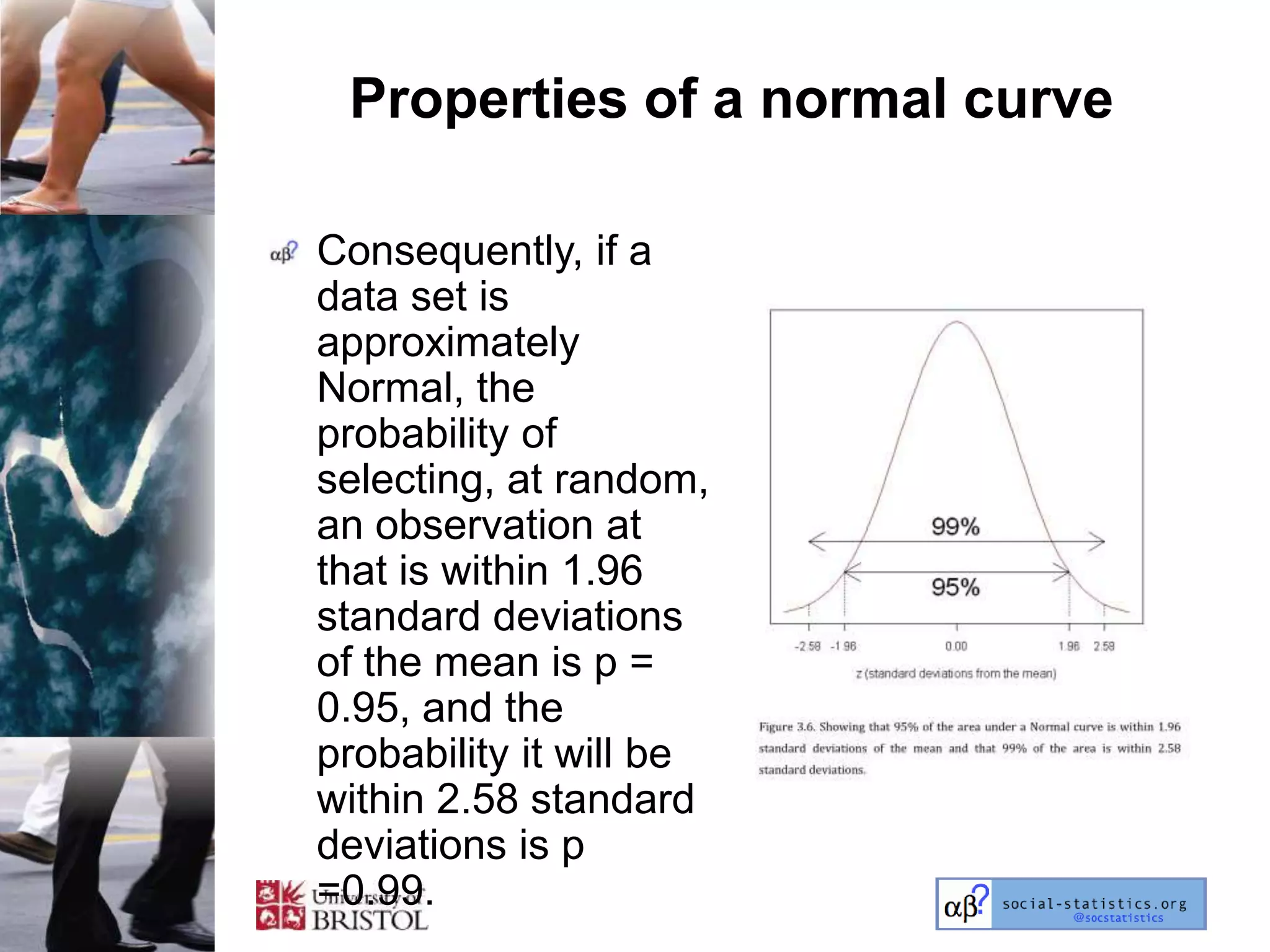
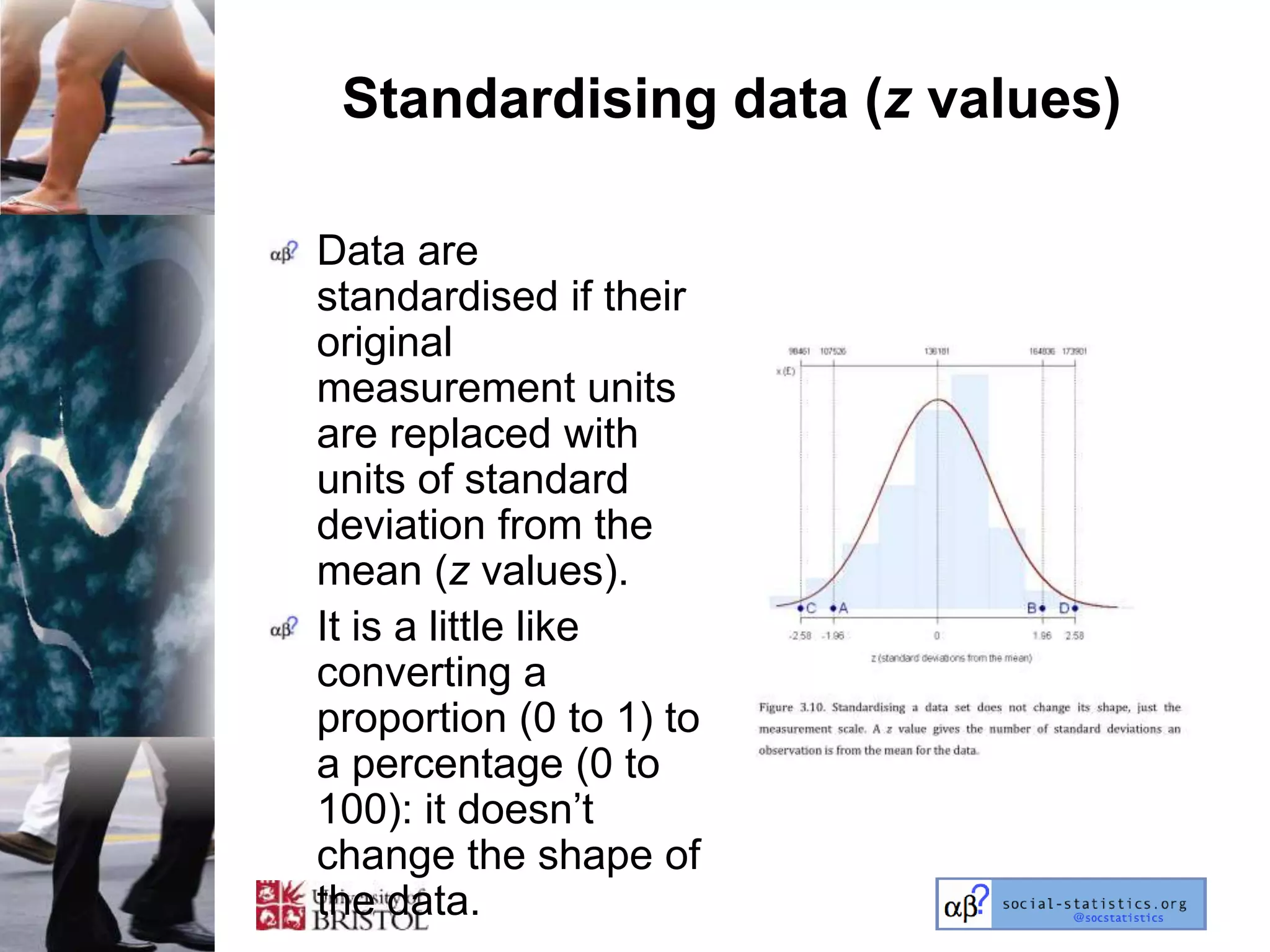
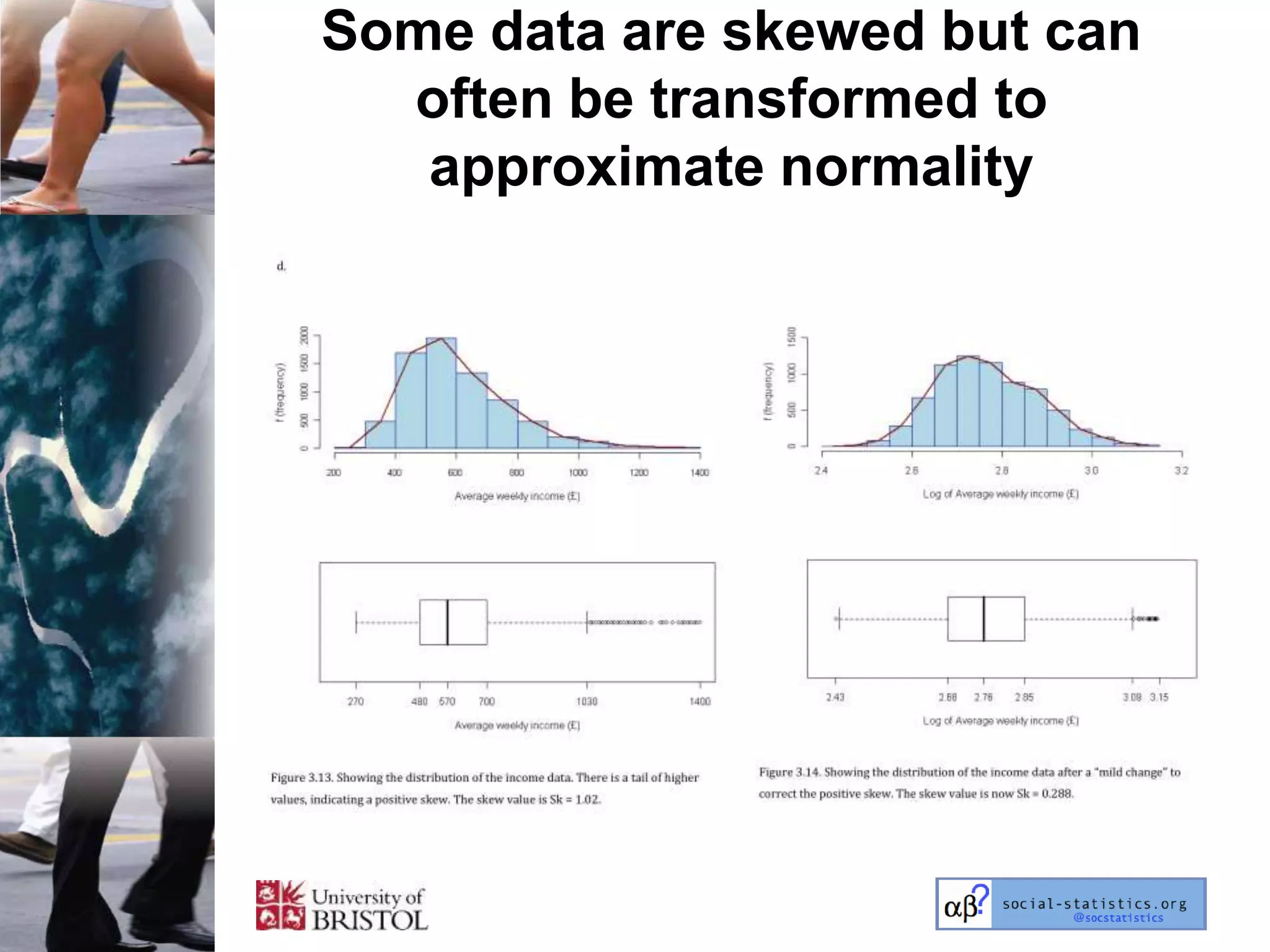
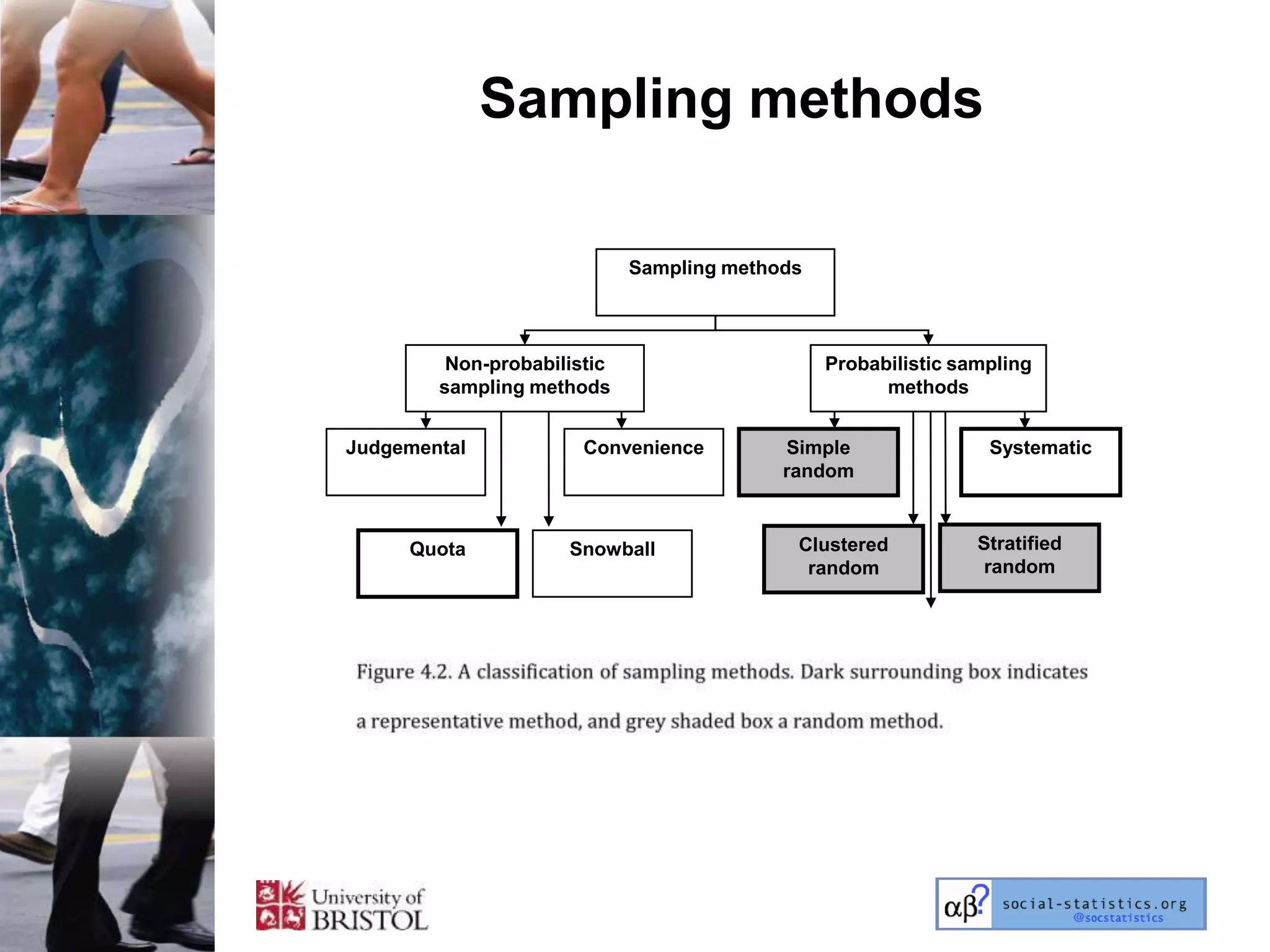
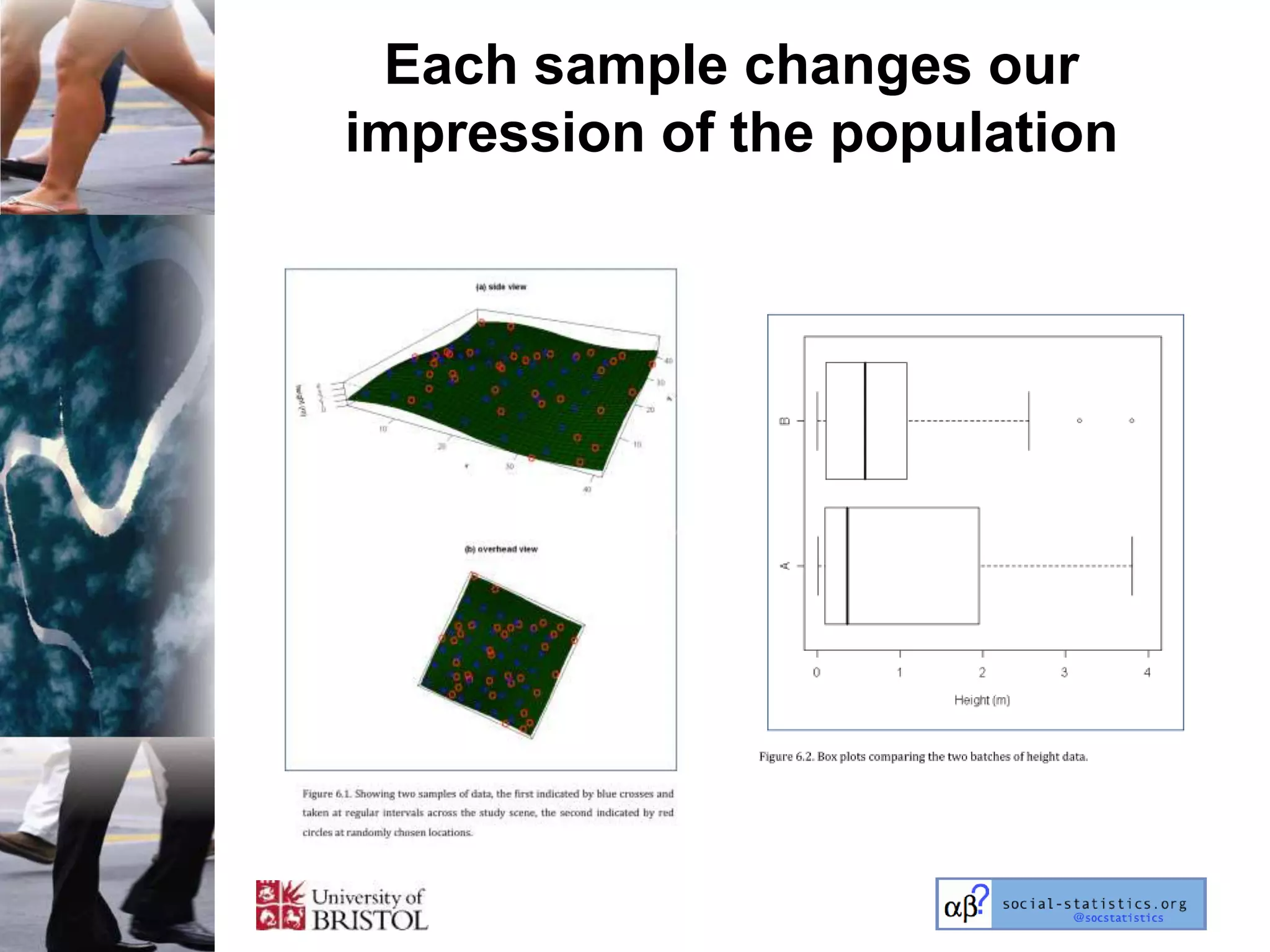
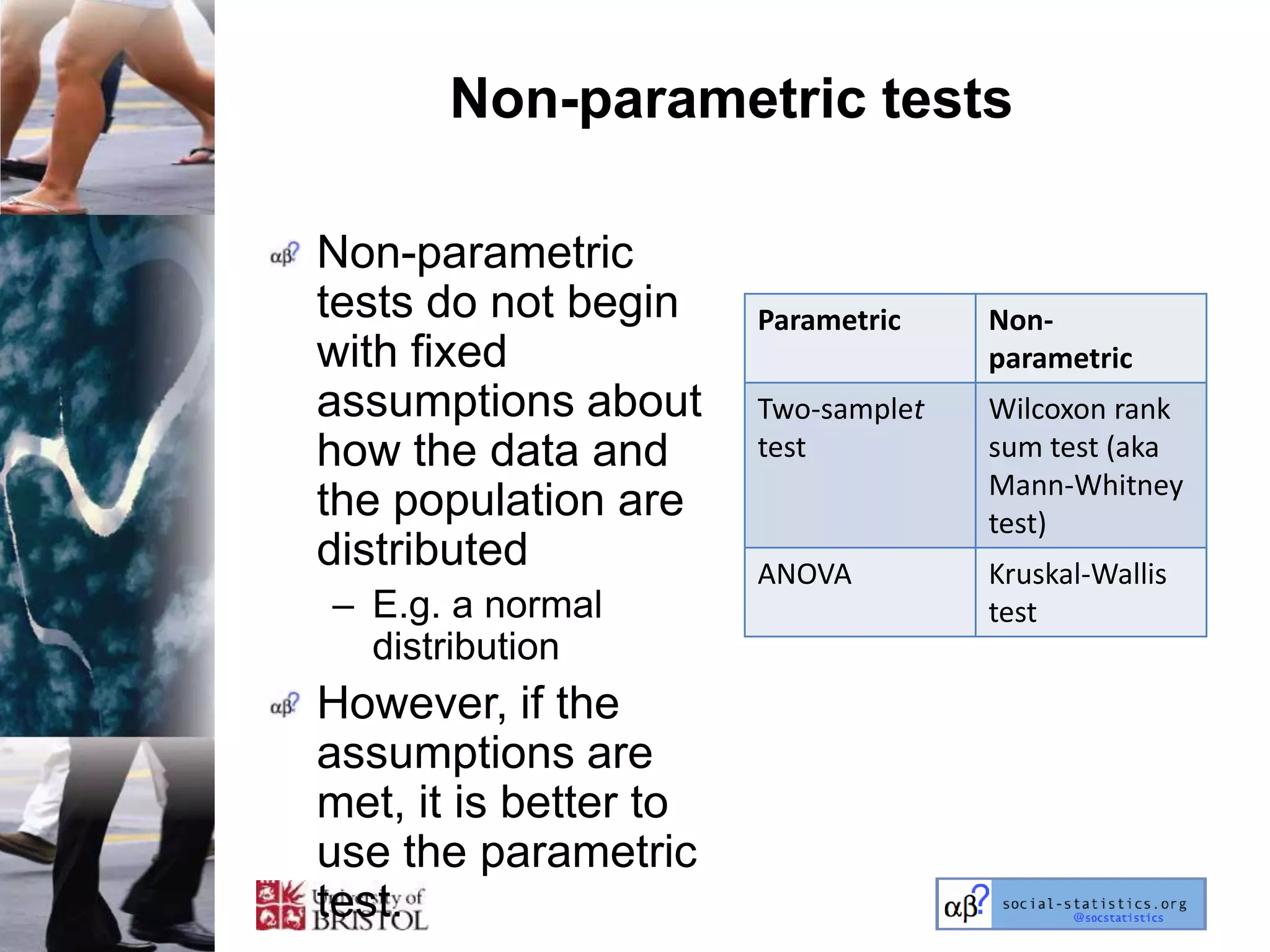
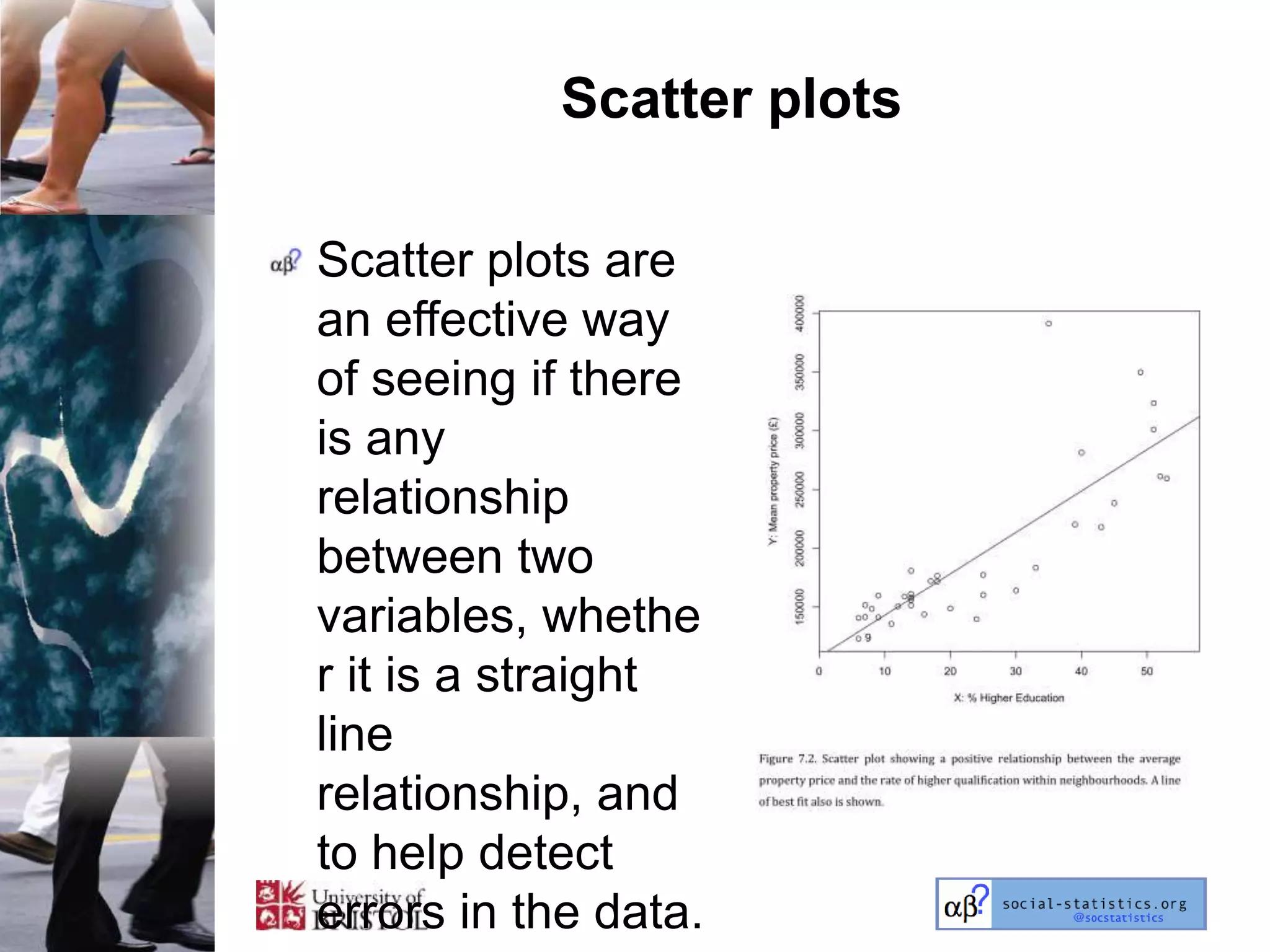
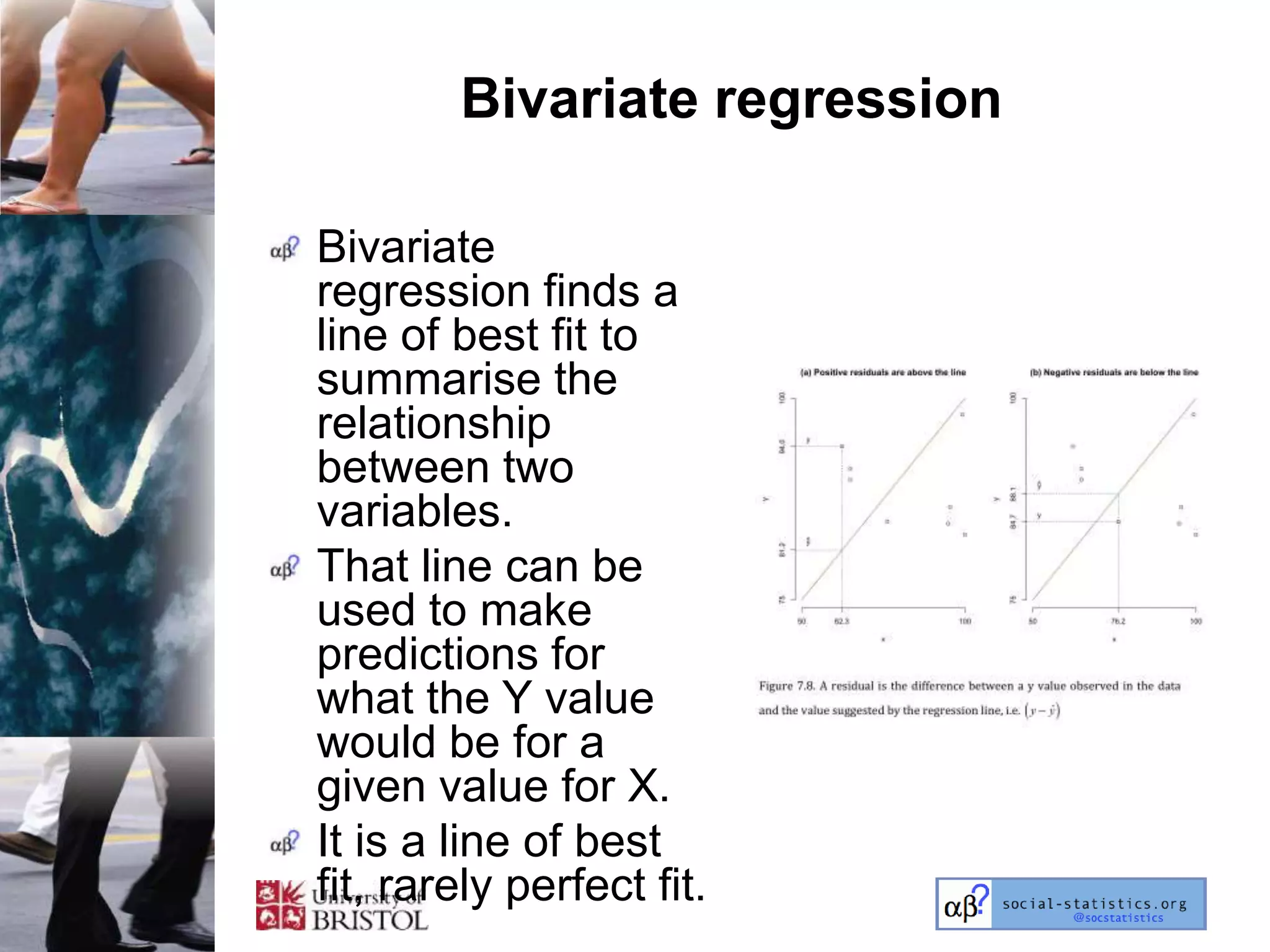
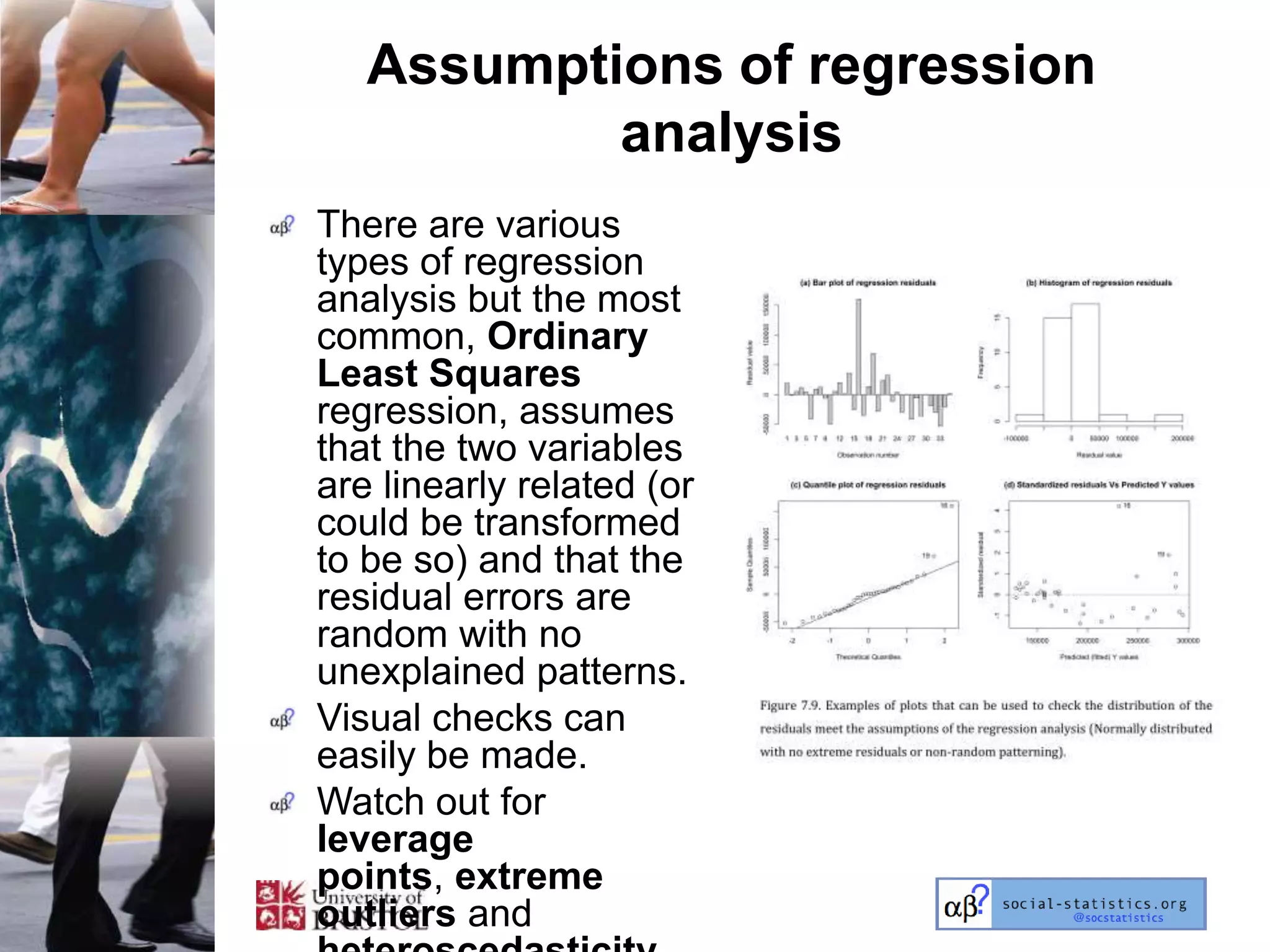
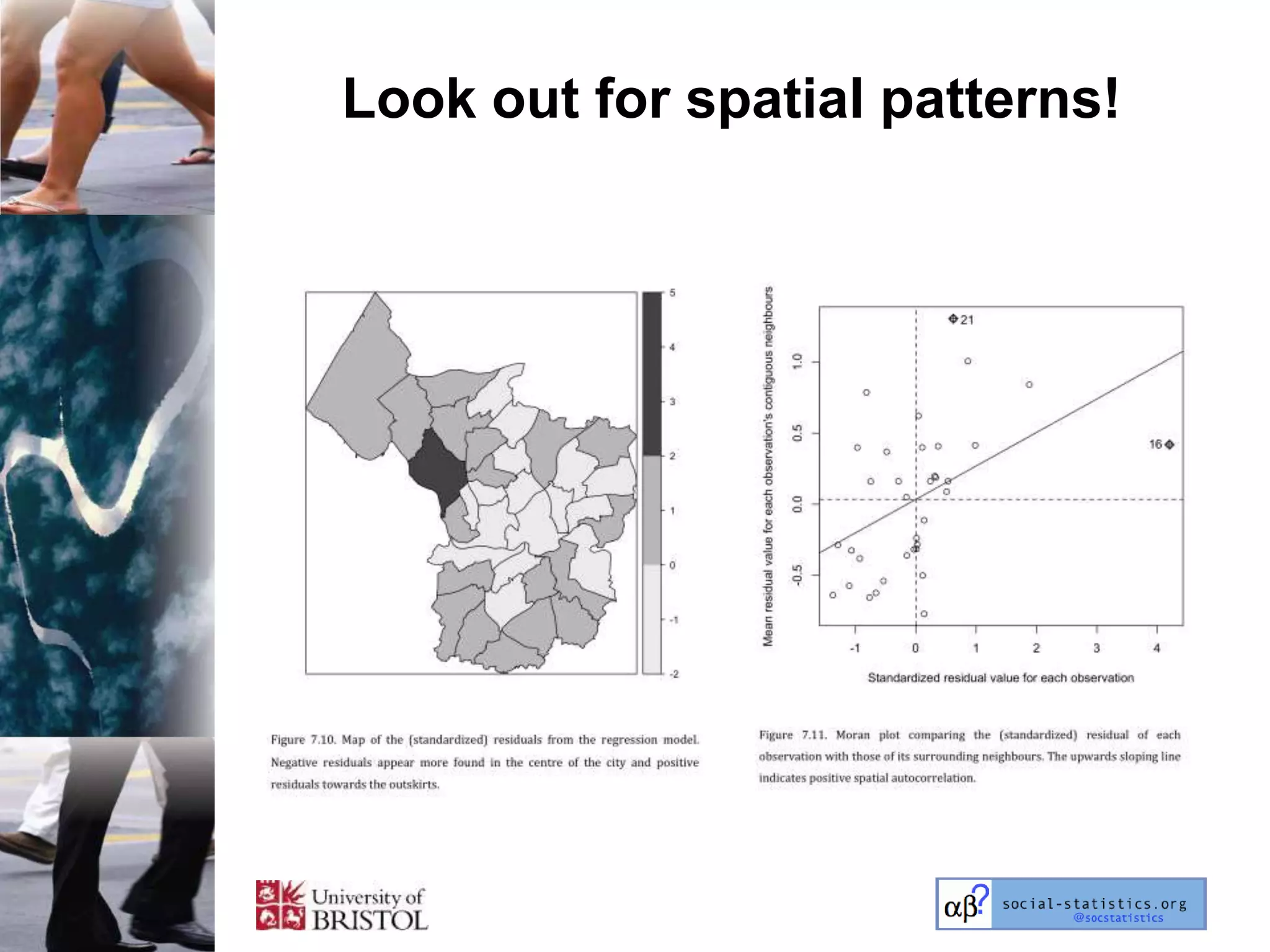
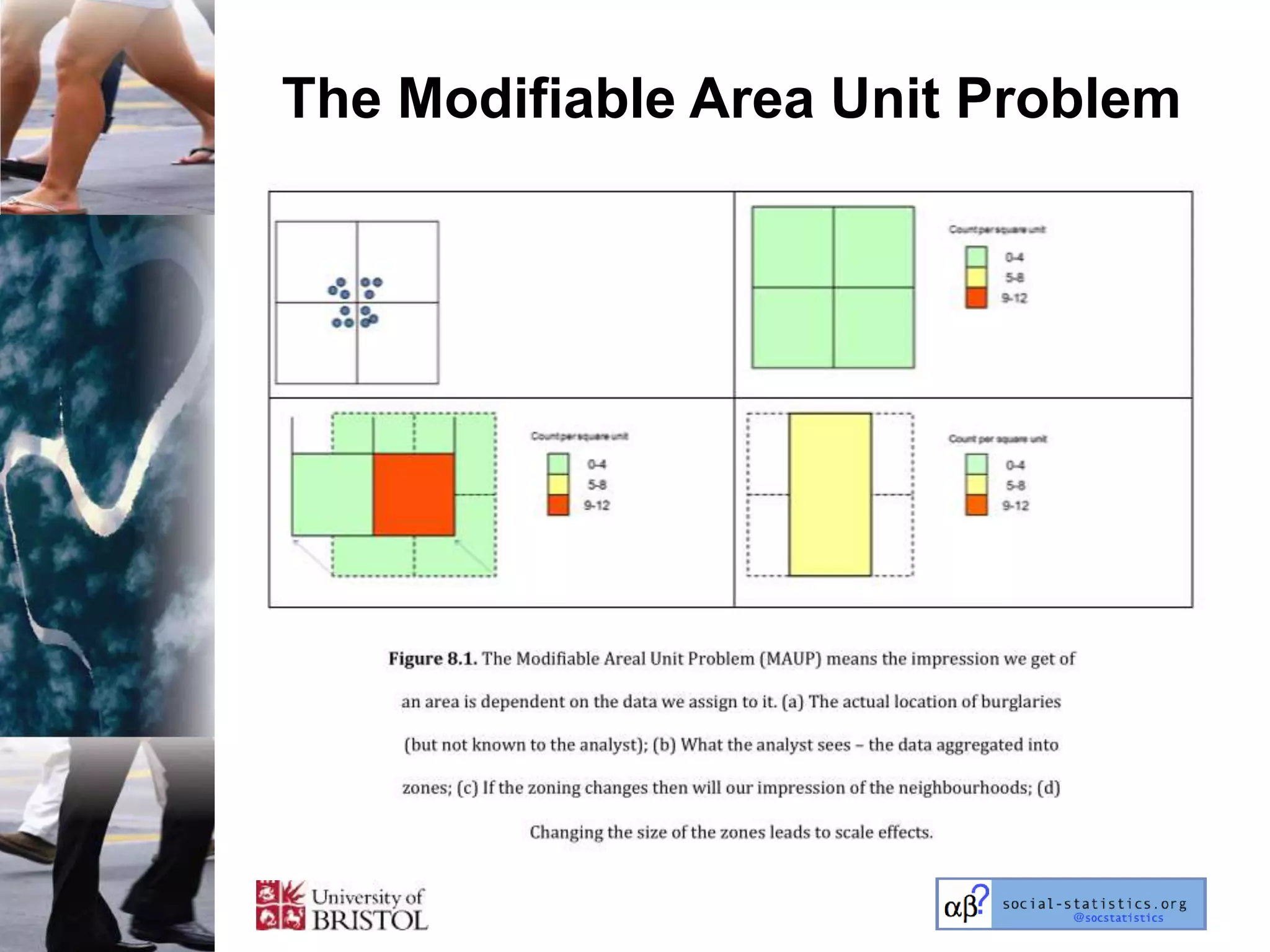
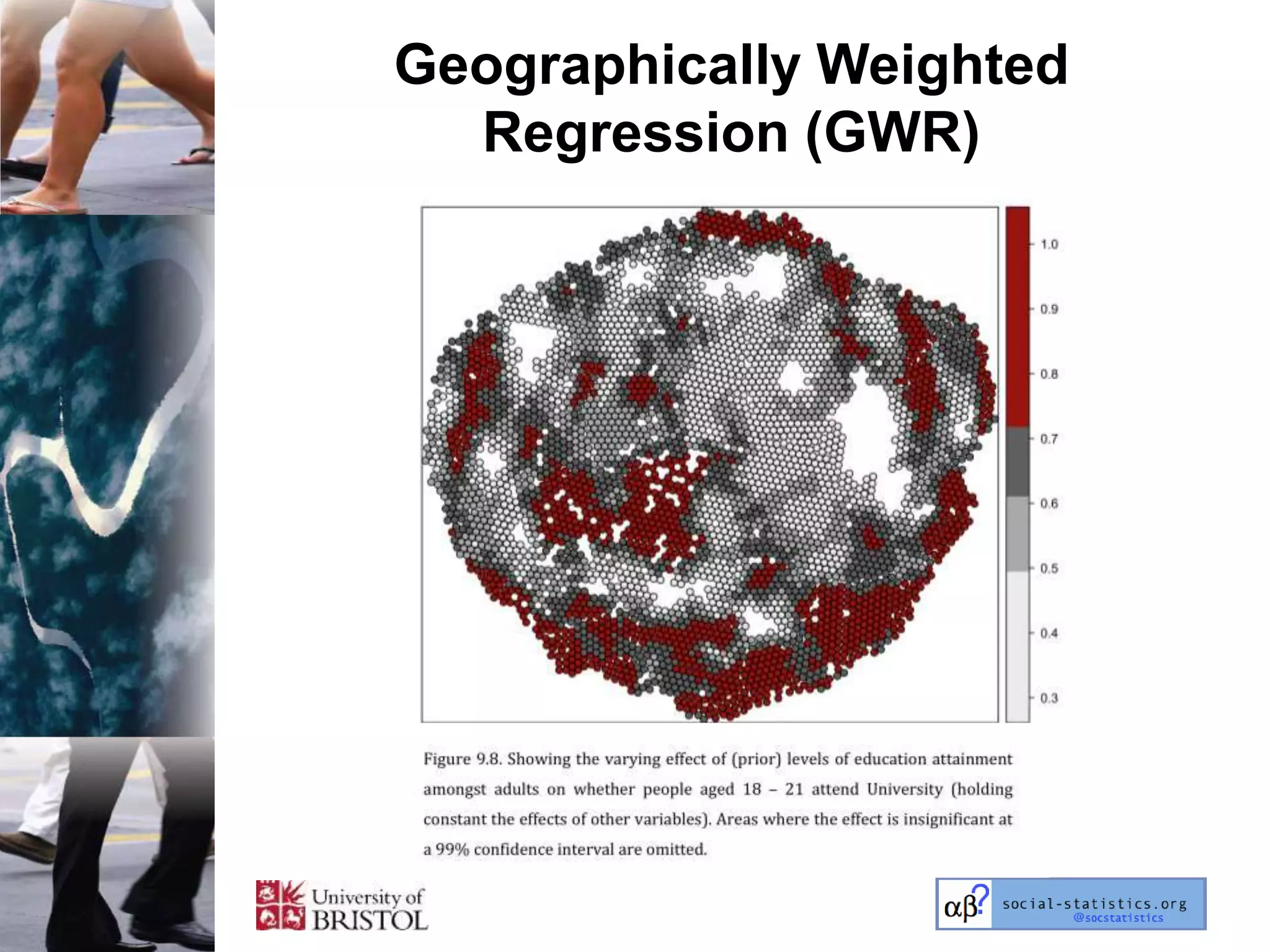
The document outlines an introductory lecture course on statistics for geography and environmental science by Richard Harris and Claire Jarvis, exploring various modules that cover essential statistical concepts and methods. It emphasizes the importance of statistics as a transferable skill for social and political debate, as well as the necessity for proper sampling, data analysis, and hypothesis testing. The course material is based on the accompanying textbook and is available for non-commercial educational use with specified restrictions.