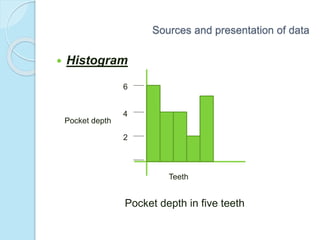
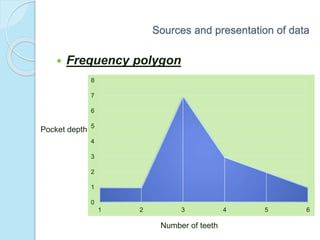
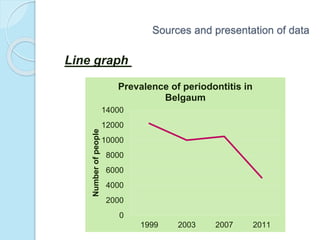
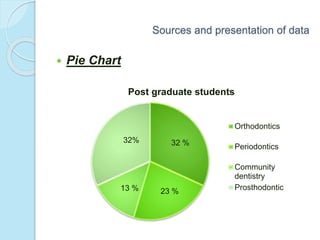
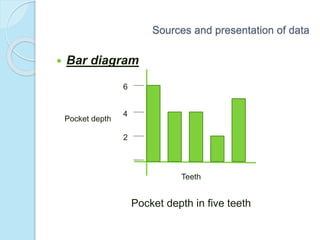
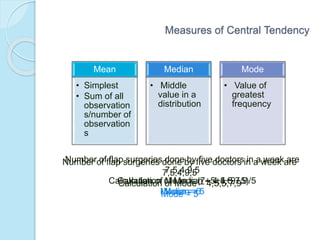
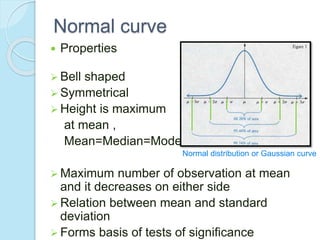
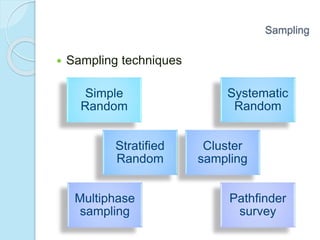
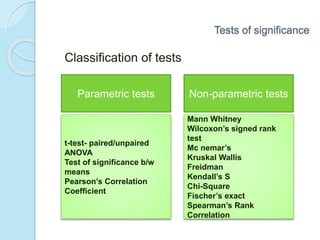
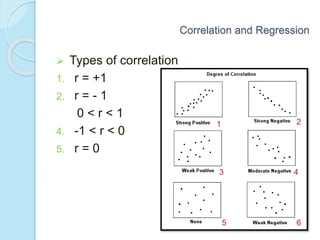
This document provides an overview of key concepts in biostatistics. It begins with introductions to terminology, sources and presentation of data, and measures of central tendency and dispersion. It then discusses the normal curve, sampling techniques, and types of tests of significance including t-tests, ANOVA, and non-parametric tests. The document provides examples and explanations of commonly used statistical analyses for comparing means and assessing relationships in data.

1. BIOSTATISTICS

2. Contents
 Introduction
 Terminologies
 Sources & Presentation of Data
 Measures of Central Tendency
 Measures of Dispersion
 Normal curve
 Sampling
 Tests of significance
 Correlation & regression
 Conclusion

3. Introduction
 Statistics – Statista (Italian)
Statistik (German)
John Graunt
(1620-1674)

4. Introduction
Why
Statistics?

5. Epidemiology and Statistics
Introduction

6.  Variable – X
 Constant – π, mean, standard deviation etc
 Observation – event +measurement
 Sample –
 Parameter – Summary value
Mean height, birth rate
Statistic
Terminologies

7. Terminologies
 Parametric test – population constants are
described (mean, variances)
 Non parametric test- no population
constants
- data do not follow
specific
distribution

8. Sources and presentation of data
 Collective recording of observations either
numerical or otherwise.

9. Sources and presentation of data
• By the investigator himself
• Interviews, questionnare, oral
health examination
Primary
• Data already present
• Records of OPD
Secondar
y
Classification of Data

10. Sources and presentation of data
 Nominal – Qualitative data
Male / Female
White / Black
Socio- economic status
 Ordinal – Arranged in rank / order
Ramu is taller than Ravi
and Ravi is taller than Ajay

11.  Interval – Placed in intervals or order
- Uses a scale graded in equal
increments
- Height, weight, blood pressure
 Ratio – Interval scale data is placed with
meaningful ratio
- Biomedically most significant
- Presented in frequency distribution

12. Qualitative
Quantitative

13. Sources and presentation of data
Methods of presentation
Tabulation Diagrams

14.  Tabulation
 Most common way – frequency distribution
table
 Important step in statistical analysis
 Presents a large amount of data – concisely
 Quantitative and qualitative data
Sources and presentation of data

15.  Diagrams
• Through graphs
• Histogram, frequency polygon,
frequency curve, line graph, scatter or
dot diagram
Quantitative
• Through diagrams
• Bar diagrams, pie diagram, picture
diagram, map diagram
Qualitative
Sources and presentation of data

16.  Histogram
Teeth
Pocket depth
Pocket depth in five teeth
Sources and presentation of data
2
4
6

17.  Frequency polygon
0
1
2
3
4
5
6
7
8
1 2 3 4 5 6
Pocket depth
Number of teeth
0
1
2
3
4
5
6
7
8
1 2 3 4 5 6
Sources and presentation of data

18. 0
2000
4000
6000
8000
10000
12000
14000
1999 2003 2007 2011
Numberofpeople
Prevalence of periodontitis in
Belgaum
Sources and presentation of data
Line graph

19.  Pie Chart
Post graduate students
Orthodontics
Periodontics
Community
dentistry
Prosthodontic
Sources and presentation of data
32% 32 %
23 %13 %

20.  Bar diagram
Teeth
Pocket depth
Pocket depth in five teeth
Sources and presentation of data
2
4
6

21. Measures of Central
Tendency
 The single estimate of a series of data that
summarizes the data is known as
parameter.
 Objective : Condense the entire mass of
data
Facilitate comparison
 3 types:
Mean Median Mode

22. Measures of Central Tendency
Mean
• Simplest
• Sum of all
observation
s/number of
observation
s
Median
• Middle
value in a
distribution
Mode
• Value of
greatest
frequency
Number of flap surgeries done by five doctors in a week are
7,5,4,9,5
Calculation of Mean = (7+5+4+9+5)/5
Mean = 6
Number of flap surgeries done by five doctors in a week are
7,5,4,9,5
Calculation of Median – 4,5,5,7,9
Median = 5
Number of flap surgeries done by five doctors in a week are
7,5,4,9,5
Calculation of Mode – 4,5,5,7,9
Mode = 5

23. Measures of Dispersion
 Measures of central tendency – single
value to represent data
 Dispersion - degree of spread or variation
of the variable about the central value.
 3 types
Range
Standard
deviation
Coefficien
t of
variation

24. Measures of Dispersion
 Range
 Simplest method
 Difference between the value of the
smallest item to the value of the largest item

25.  Standard deviation
 Most important and widely used
 Root mean square deviation
 Summary measure of the differences of
each observation from mean of all
observations
 Greater the deviation – greater the
dispersion
Lesser the deviation – greater uniformity
Measures of Dispersion

26.  Coefficient of variation
 Standard deviation – deviation within a
series.
 Compare two or more series, with different
units of measurement
Coefficient of variation = Standard deviation
Mean
100
Measures of Dispersion

27. Normal curve
 Properties
 Bell shaped
 Symmetrical
 Height is maximum
at mean ,
Mean=Median=Mode
 Maximum number of observation at mean
and it decreases on either side
 Relation between mean and standard
deviation
 Forms basis of tests of significance
Normal distribution or Gaussian curve

28. Sampling
 Need for sampling ??
 Two types of sample selection
Purposive Random

29.  Sampling techniques
Simple
Random
Systematic
Random
Stratified
Random
Cluster
sampling
Multiphase
sampling
Pathfinder
survey
Sampling

30. Sampling
1. Simple random sampling
2. Systematic random sampling
 One unit is selected at random and all
other at evenly spaced intervals
 No periodicity of occurrence
Lottery
Table of Random
numbers

31. 3. Stratified Random sampling
 When the population is not homogenous.
 Population is divided in homogenous
groups, followed by simple random
selection
 Merits :
Representative sample from each strata is
secured.
Gives great accuracy
Sampling

32.  Disadvantage:
Utmost care has to be taken while dividing
the population into strata (regarding
homogeneity of the strata)
Sampling

33.  Cluster sampling
 Natural clusters – school, village etc.
 From these clusters- the entire population is
surveyed
 Advantages: Simple
Involves less time and cost
 Disadvantage : Higher standard error
Sampling

34.  Multiphase sampling
 Part of information is collected from whole
sample and a part from sub-sample.
 Advantages : less expensive
less laborious
more purposeful
Sampling

35. All patients on OPD examined (first phase)
Only those suffering chronic periodontitis
selected (second phase)
Only those within the age group of 35-45
years selected (third phase)
Sample size keeps on becoming smaller
Sampling

36.  Pathfinder survey
 A specified proportion of the population
 Stratified cluster sampling
 Subjects in specific index age groups are
selected.
 Helps to assess
1. The variations in severity of disease in
different subgroups
2. Picture of age profiles of various oral
diseases.
Sampling

37. Sample size
 Optimum size of sample based on
following:
1. Approximate idea of estimate of
characteristics- Obtained from previous
studies or pilot studies prior to starting
study.
2. Knowledge about the estimate of
precision – probability level for precision.
Sampling
precision= √n / s (s=SD)

38.  Sample size
n = Sample size,
p = Approx prevalence rate,
L = Permissible error in p estimation,
Z α = Normal value for probability level.
Sampling
Zα
2 * p * (1-p)
L2
n =

39.  If p = 10% , investigator allows an error of
prevalence rate of 20%,
n =900
Sampling
4* 0.1*(0.9)
(0.01)2
n =

40. Tests of significance
 Sampling variability
 Tests of hypothesis

41. Tests of significance
 Null Hypothesis and Alternative
Hypothesis
Null hypothesis
• No real
difference
• Difference
found -
accidental
Alternative
hypothesis
• Real difference
present

42.  Level of significance
 Probability level – P
 Small P value
Tests of significance
– Null Hypothesis rejected
P-value
0.05-0.01 Statistically significant
< 0.01 Highly statistically significant
< 0.001 or 0.005 Very highly statistically significant

43.  Degree of freedom
 Number of independent members in a
sample
Degree of freedom = (n – 1)

44. Tests of significance
 Standard error
 Standard error of mean – Gives the
standard deviation of means of various
samples from the same population
 Measure of chance variation
Mean error or mistake
Standard error of mean = Standard
deviation
n

45.  Types of error
Hypothesis
Accept Reject
True Right Type I error
False Type II error Right
Decision
Tests of significance

46.  Steps involved in testing of hypothesis
1. State Null and Alternative hypothesis
2. Calculate t, F, χ2
3. Determine degree of freedom
4. Find probability P using appropriate data
5. Null hypothesis rejected – p < 0.05
Null hypothesis accepted – p > 0.05
Tests of significance

47. t-test- paired/unpaired
ANOVA
Test of significance b/w
means
Pearson’s Correlation
Coefficient
Mann Whitney
Wilcoxon’s signed rank
test
Mc nemar’s
Kruskal Wallis
Freidman
Kendall’s S
Chi-Square
Fischer’s exact
Spearman’s Rank
Correlation
Parametric tests Non-parametric tests
Tests of significance
Classification of tests

48.  These are mathematical tests
 They assess the probability of an observed
difference, occurring by chance
 Most commonly used tests are -
Z test, t test, χ2 test
Tests of significance

49.  Student’s t test
 Designed by W.S. Gossett
 Applied to find the difference between two
means
 Criteria for applying t test
1. Random samples
2. Quantitative data
3. Sample size < 30
4. Variable normally distributed
Tests of significance

50.  Unpaired t test
 Data of independent observations made on
individuals of two different groups or
samples
 Checks sampling variability between
experimental and control groups
 e.g. checking sampling variability between
SRP+ subgingival irrigation (experimental
group) and SRP alone (control group)
Tests of significance

51.  Paired t test
 Paired data of independent observations
from one sample only who gives a pair of
observations.
 E.g. sampling variability in the decrease in
the microbial load before and after
administration of antimicrobial therapy.
Tests of significance

52.  Wilcoxon’s signed rank test
 Developed by Frank Wilcoxon
 Alternative to the Student’s paired t test
Tests of significance

53.  Analysis of Variance (ANOVA) test
 Compares more than two samples drawn
from corresponding normal population
 E.g : to check if different agents used for
subgingival irrigation have an effect on the
decrease in microbial load.
Use 3 groups (chlorhexidine , saline,
povidone iodine)
Tests of significance

54.  If the difference between their means is
significant - different agents used do have
different effect on the decrease in microbial
load.
 To assess this difference in means- ANOVA
test is important
Tests of significance

55.  Chi – square test
 Developed by Karl Pearson
 Data measured - terms of
attributes/qualities- intended to test if
difference is due to sampling variation
 Involves calculation of a quantity
 3 important applications:
1. Proportion
2. Association
3. Goodness of fit
Tests of significance

56.  E.g. : Two groups are present
Oral hygiene Oral
hygiene
instructions given instructions
not
given
To assess if there is an association between
gingivitis and oral hygiene instructions.
Tests of significance

57. Correlation and Regression
 Correlation
 The relationship between two quantitatively
measured variables
 Change in the value of one variable, results
in a change in the other
 Magnitude or degree of relationship
between two variables is called correlation
coefficient (r)

58. Correlation and Regression
Pearson’s correlation coefficient
Pearson’s correlation coefficient
Variables are normally distributed
(height and weight)
Variables are not normally distributed
(IQ, income)
 Pearson’s correlation coefficient

59. Correlation and Regression
 Types of correlation
1. r = +1
2. r = - 1
0 < r < 1
4. -1 < r < 0
5. r = 0
1
65
43
2

60.  Regression
 Regression coefficient – measure of change
in one character (dependent variable - Y) ,
with one unit change in the independent
character (X)
 Denoted by “b”
 Regression line
Correlation and Regression

61.  Change of dependent variable in linear way
Y = a+bX
Y = dependent variable
a = Y value
b = regression coefficient
X = independent variable
Correlation and Regression

62. Conclusion
Clinician Facts
Figures
Statistics

63. References
 B K Mahajan ; Methods in Biostatistics,
6th edition
 Soben Peter ; Essentials of Preventive and
Community dentistry , 2nd edition
 K. Park ; Parks Textbook of Preventive And
Social medicine , 19th edition