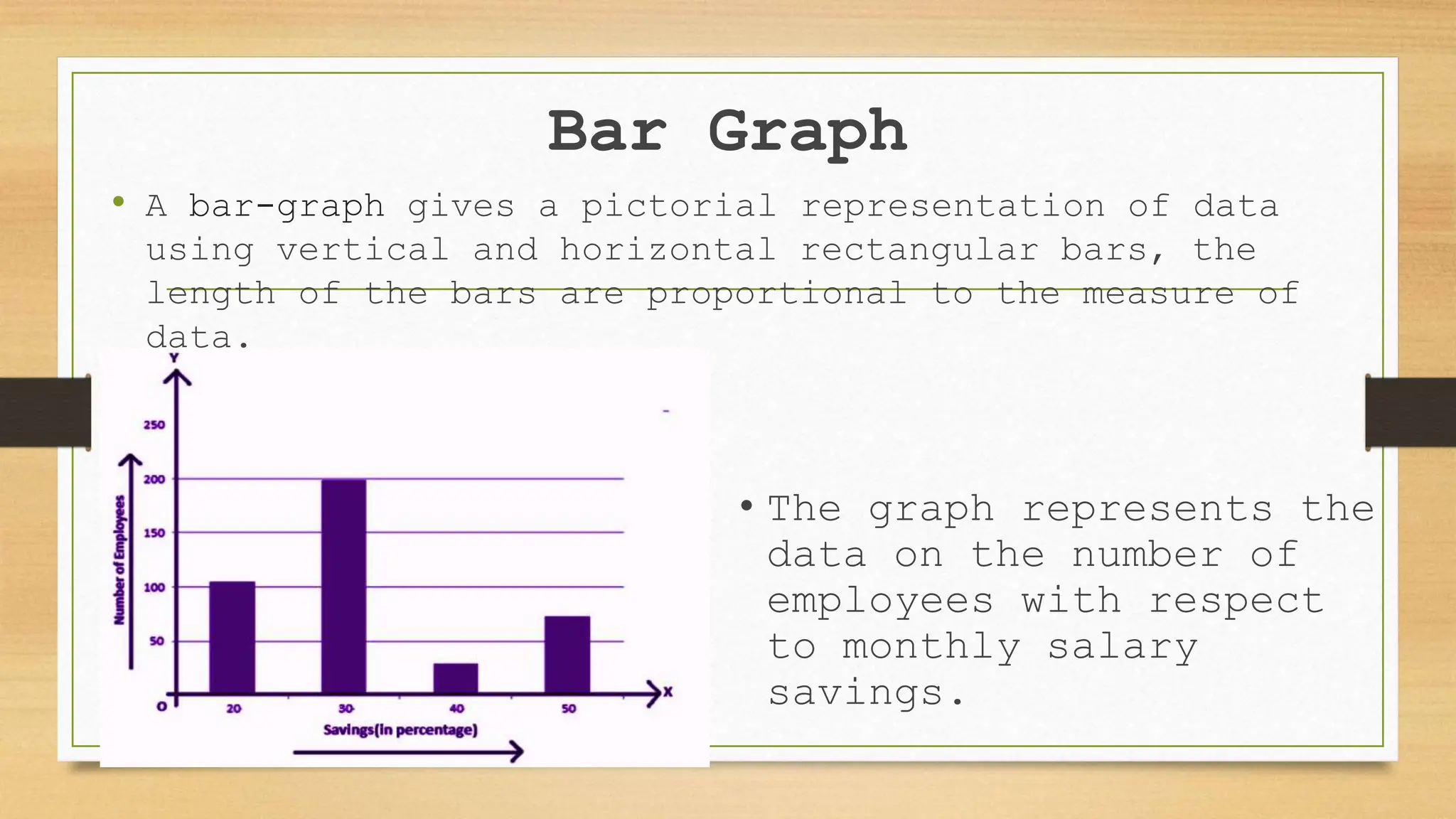
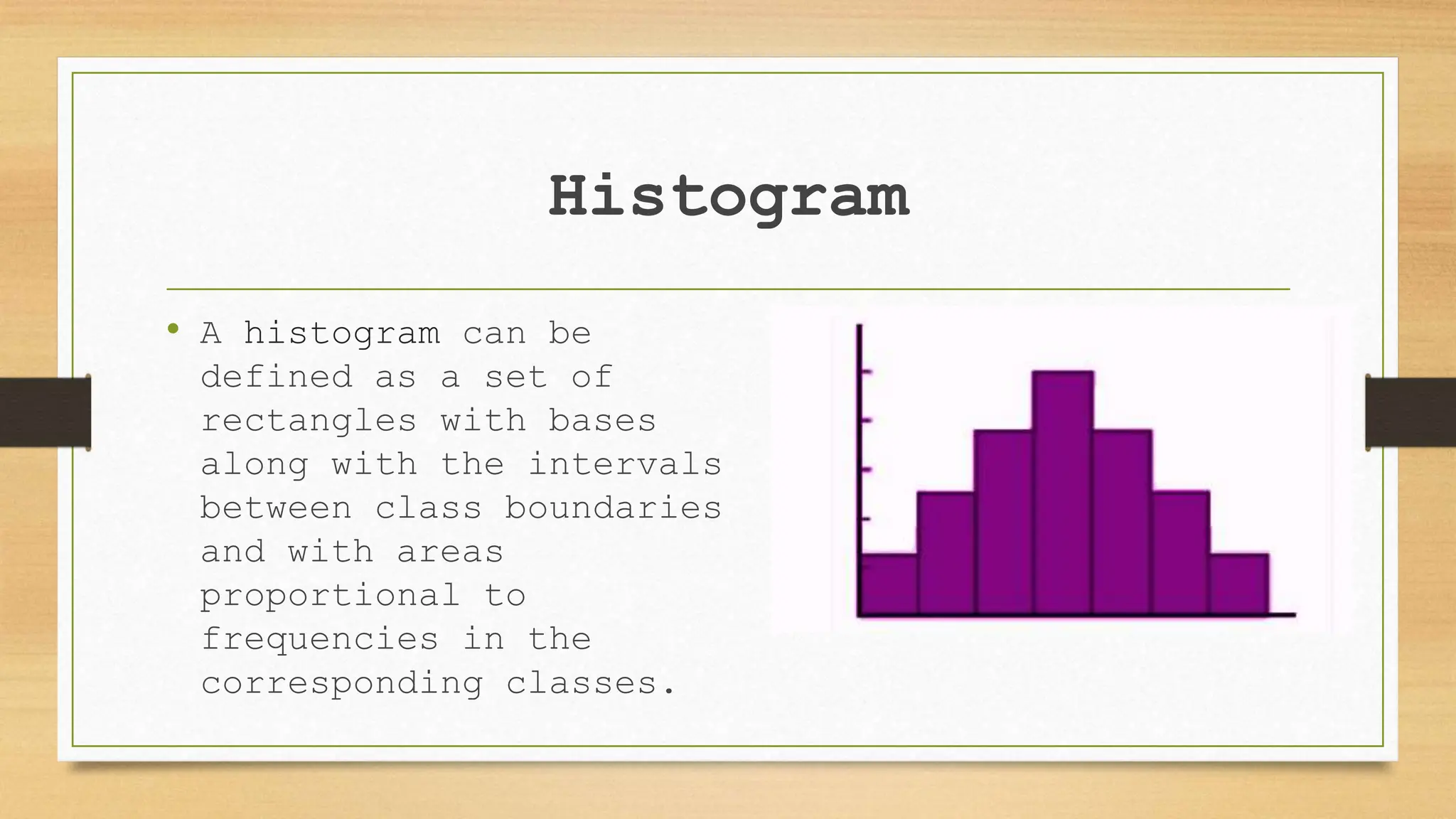
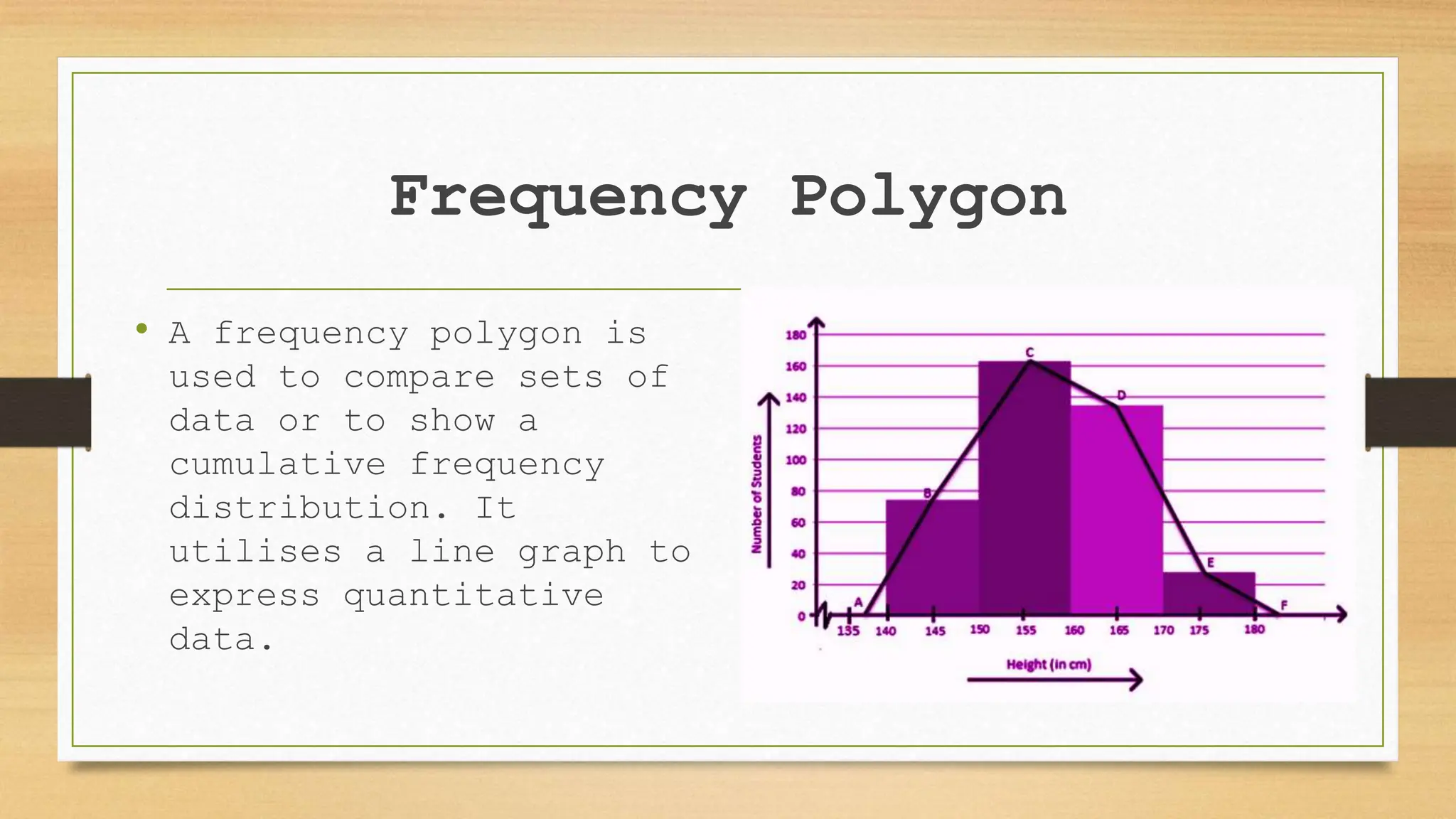
This document discusses how to collect, present, and analyze statistical data. It provides examples of collecting data on student characteristics like age and exam scores. Data can be presented through tables that group values into frequency distributions to calculate quantities like the number of students scoring above a threshold. Graphs like bar graphs, histograms, and frequency polygons can also represent grouped data visually. Measures of central tendency - mean, median, and mode - are introduced to summarize typical values in a data set. Formulas and examples are given for calculating each of these statistical measures.

1. Statistics

2. Collection of Data
• The meaning of a collection of data is to gather
some sort of information to prepare a report or to
do some analysis on them. Some examples are:
• Group of students under age 15 in a class.
• Height of 30 students in your class
• Number of family members in a house
• Age of the students in a class

3. Presentation of Data
• After collecting the data for a certain group, we
have to now learn to present it.
• The presentation should be such that it should be
meaningful, easily understood by everyone and the
main features could be captured at a glance or by
a single view.

4. Example: Suppose an exam was conducted for
a class of 50 students. The marks obtained
out of 100, by the students here are:
12, 23, 45, 55, 10, 33, 65, 78, 89, 22,44,
55, 77, 88,
35, 65, 63, 61, 84, 89,34, 27, 90, 65, 67,
45, 78, 98,
66, 77,31, 41, 61, 68, 86, 34, 54, 59, 78,
89,50, 29,
58, 63, 72, 87, 34, 65, 48, 91

5. • Hence, from the above-grouped frequency distribution
table, we can calculate the number of students who
scored above 40 marks = 11+17+10 = 38

6. Graphical Representation of
Data
The grouped data of a collection of data can be
represented using the graph as well. There are
three ways by which we can represent the data in
graphical form, which are;
1.Bar Graph
2.Histogram
3.Frequency Polygons

7. Bar Graph
• A bar-graph gives a pictorial representation of data
using vertical and horizontal rectangular bars, the
length of the bars are proportional to the measure of
data.
• The graph represents the
data on the number of
employees with respect
to monthly salary
savings.

8. Histogram
• A histogram can be
defined as a set of
rectangles with bases
along with the intervals
between class boundaries
and with areas
proportional to
frequencies in the
corresponding classes.

9. Frequency Polygon
• A frequency polygon is
used to compare sets of
data or to show a
cumulative frequency
distribution. It
utilises a line graph to
express quantitative
data.

10. Measures of central tendency
There are majorly three measures of central
tendency:
• Mean
• Median
• Mode

11. Mean
Mean is the average of the
given set of data.
x̄=∑ x/n
Where n is the number of
observations

12. Median
• The median is that value which divides the given
number of observations into exactly two parts.
First, the data set has to be arranged in an
order, either ascending or descending. There are
again two conditions here:
• If the number of observations is odd, then;
• Median = [(n+1)/2]th observation or term
• If the number of observations is even, then the
median will be mean of (n/2)th term and
((n/2)+1)th term.

13. Mode
• The mode represents the frequently
occurring value in the dataset.

14. Example: Find the mean, median and mode of the following
data set.
2,3,6,7,4,5,3,8,3,9
Solution: Mean is the average of the given data;
x̄ = (2+3+6+7+4+5+3+8+3+9)/10 = 50/10 = 5
Now, to find the median, we need to arrange the data in
ascending order.
2,3,3,3,4,5,6,7,8,9
Since, here the number of observations is even,
therefore, the median will be the mean of the two middle
terms.
Median = (4+5)/2 = 9/2 = 4.5
Mode = 3, since 3 is repeated here maximum number of
times.

15. Thank
You
S Vaishali