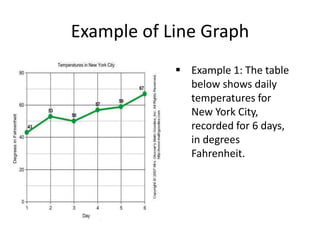
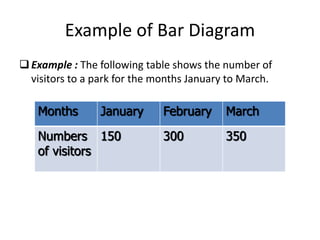
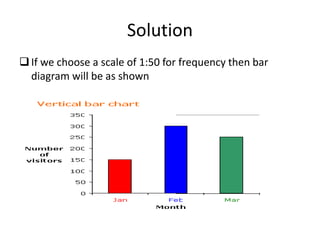
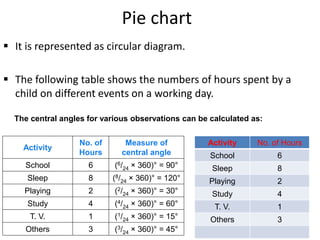
This document provides an overview of biostatistics. It defines biostatistics as the application of statistics to biology, medicine, and public health. It discusses different types of data, measures of central tendency including mean, median and mode, and graphical representations such as line graphs, bar diagrams and pie charts. The document emphasizes the important role of biostatistics in medical research and clinical decision making. It acknowledges deficiencies in biostatistical literacy among medical students and professionals.

1. Biostatistics
Akhilesh Kumar Maurya
M.Sc. 3rd Semester
Department of Biotechnology
V.B.S. Purvanchal University
Jaunpur[U.P.] 222003

2. Contents
 Introduction
 Data and types
 Measures of central tendency
 Role of biostatistics
 Conclusion
 Reference

3. Introduction
 Biostatistics is the application of statistics to biology.It is
frequently associated with applications to medicine and
to agriculture.
 Biostatistics may be defined as the application of
statistical methods to the problems of biology ,including
human biology ,medicine and public health .
 It is also known as biometry (literally meaning ‘biological
measurement’)

4. Data
 The information collected through census and surveys or
in a routine manner or resource is called a raw data.
 The word data means information .
 Raw data is like a raw rice .
 A raw rice has to be cooked properly and tastefully before
it is n and digested .
 Similarly , a raw data has to converted in to proper form
such as tabulation ,frequency distribution form , etc.

5. Types of Data
 There are two types statistical data-
1-Primary data
2-Secondary data
 Primary data-It is a data collected by a particular person
or organization for his own use from the primary source.
 Secondary data-It is the data collected by some other
person or organization for their own use but the
investigator also gets if for his use
 In other words ,the primary data are those data which
are collected by you to meet your own specific purpose.

6. Graphical representation of data
 The representation of quantitative data suitably through
charts and diagrams is known as Graphical
Representation of Statistical Data.
 Graphs include both charts and diagrams.
 A graphic representation is the geometrical image of a
set of data . It is a mathematical picture .

7. Advantage of Graphical Representation
 It is easily understood by all.
 The data can be presented in a more attractive form appealing
to the eye.
 It shows relationship between two or more sets of figures.
 It has a universal applicability.
 Various valuable statistics like median ,mode, quartiles , may be
easily observed.
 It may help in the proper estimation , evaluation and
interpretation of the characteristics of items and individuals.

8. Disadvantages of Graphical
Representation
 It takes a lot of time to prepare a graph.
 A graph does not show all the facts (data) in detail.
 It depicts only approximate values.

9. Graphical Representation of
Ungrouped Data
 For the ungrouped data (data not grouped into frequency
distribution) we usually make use of the following
graphical representation:
1-Line graphs
2-Bar graph or Bar diagrams
3-Circle graph or Pie diagrams
4-Pictograms

10. 1-Line Graph
 Line graph are simple mathematical graphs that are
drawn on the graph paper by plotting the data
concerning one variable on the horizontal x-axis and
other variable of data on the vertical y-axis .
 The help of such graphs the effect of the variable upon
another variable during an experimental or normative
study may be clearly demonstrated .
 The construction of these graphs can be understood
through the following example;

11. Example of Line Graph
 Example 1: The table
below shows daily
temperatures for
New York City,
recorded for 6 days,
in degrees
Fahrenheit.

12. Bar Diagram
 A bar graph is a chart that uses bars to show comparisons between
categories of data.
 The bars can be either horizontal or vertical.
 Bar graphs with vertical bars are sometimes called vertical bar graphs.
 A bar graph will have two axes. One axis will describe the types of
categories being compared, and the other will have numerical values
that represent the values of the data.
 It does not matter which axis is which, but it will determine what bar
graph is shown.
 If the descriptions are on the horizontal axis, the bars will be oriented
vertically, and if the values are along the horizontal axis, the bars will be
oriented horizontally.

13. Example of Bar Diagram
Example : The following table shows the number of
visitors to a park for the months January to March.
Months January February March
Numbers
of visitors
150 300 350

14. Solution
If we choose a scale of 1:50 for frequency then bar
diagram will be as shown

15. Measures of Central Tendency
 The measure of central tendency is defined as: “It is a
sort of average or typical value of the series and its
function is to summarise the series in terms of this
average value”.
 The most common measures of central tendency are:
1-Arithmetic mean or Mean
2-Median
3-Mode

16. Pie chart
 It is represented as circular diagram.
 The following table shows the numbers of hours spent by a
child on different events on a working day.
The central angles for various observations can be calculated as:
Activity
No. of
Hours
Measure of
central angle
School 6 (6/24 × 360)° = 90°
Sleep 8 (8/24 × 360)° = 120°
Playing 2 (2/24 × 360)° = 30°
Study 4 (4/24 × 360)° = 60°
T. V. 1 (1/24 × 360)° = 15°
Others 3 (3/24 × 360)° = 45°
Activity No. of Hours
School 6
Sleep 8
Playing 2
Study 4
T. V. 1
Others 3

17. Pie Chart Diagram
Now, we shall represent these angles within the circle as
different sectors. Then we now make the pie chart:

18. Characteristics of an measures central
tendency
 According to Professor G .U. Yule, a good average
must have the following characteristics
 1-It should be easy to understand and easy to
calculate .
 2-It should be based on all the observations of the
data.
 3-It should be least affected by the fluctuations of
the sampling.
 4-It should not be unduly affected by the extreme
values.
 5-It should be easy to interpret.

19. Arithmetic mean or Mean
 The mean is the average of the numbers: a calculated
"central" value of a set of numbers.
 Example: what is the mean of 2, 7 and 9?
Add the numbers: 2 + 7 + 9 = 18
Divide by how many numbers (i.e. we added 3 numbers):
18 ÷ 3 = 6
So the Mean is 6

20. Example
 These are the scores from last week's geometry test:
 90, 94, 53, 68, 79, 84, 87, 72, 70, 69, 65, 89, 85, 83, 72
 You earned a score of 72. Your mom asks you how you did on the test
compared to the rest of the class. Calculate the three measures of the
average, and decide what to tell your mom.
 Mean:

 (90+94+53+68+79+84+87+72+70+69+65+89+85+83+72)/15
 1160/15 = 77.333333333

21. Median
 Median means middle. In the study of statistics, the
median is just one way of determining the average
of a group of numbers.
 The median is the middle number in a group of
numbers. It's not as commonly used as the others,
but it can be the best 'average' to use when you
have a set of data that contains outliers.
http://study.com/academy/lesson/what-is-the-median-
definition-lesson-quiz.html

22. Example
 Examples of Median
 12, 23, 8, 46, 5, 42, 19
Mean =
The median in the above data set is 19.
http://study.com/academy/lesson/what-is-the-median-
definition-lesson-quiz.html

23. Mode
 The mode is the number that occurs most often in a set
of data.
Example -
Q. Find the mode?
5, 6, 2, 5, 8, 7, 4, 9, 1, 4
Solution:This set of numbers has 2 modes, 4 and 5; these
numbers both occur twice, while all the other numbers
occur only once.
http://study.com/academy/lesson/what-is-the-median-
definition-lesson-quiz.html

24. Role of Biostatics
 Biostatistics is a branch of applied statistics and it must be taught
with the focus being on its various applications in biomedical
research.
 It is an essential tool for medical research, clinical decision making,
and health management.
 Statisticians have long expressed concern about the slow uptake of
statistical ideas by the medical profession and the frequent misuse of
statistics when these methods are used. On the other hand, doctors
have been worried about the increasing pressure to make use of
techniques that they do not fully understand.
 The biostatistical literacy of medical students is a problem all over the
world.
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3657982/

25.  Research is an important activity for not only postgraduate (PG)
medical students but for all medical professionals. Deficient basic
biostatistical knowledge adversely affects research quality.
Inappropriate statistical methods, techniques, and analysis results
in time and cost lost and, most importantly, from the perspective of
scientific ethics, does harm to science and humanity.
 Writing on the teaching and learning of medical statistics in South
Africa, Standerd remarked that ‘medical practitioners were totally
intimidated by the idea of statistics.’
 Surveys on this issue are uncommon in the literature.

26. References-

27. Acknowledgement
Dr.Pradeep Kumar Sir(Assistant Professor)
Department of Biotechnology
V.B.S.Purvanchal University
Jaunpur[222003] U.P.

28. THANK YOU