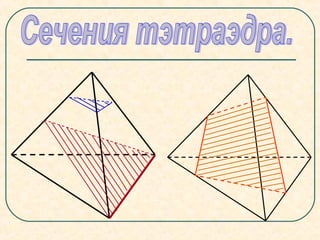
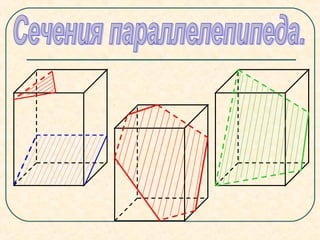
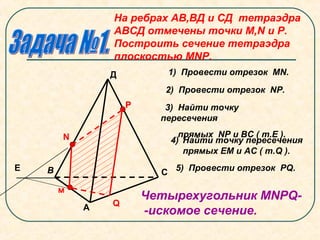
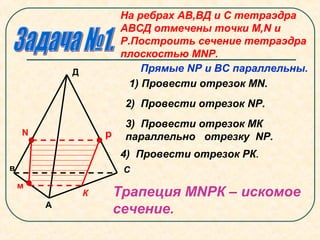
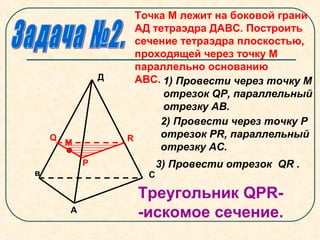
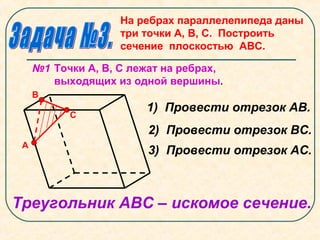
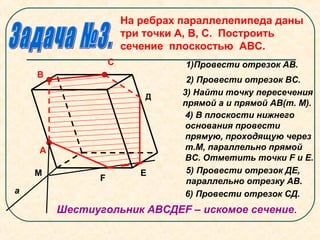
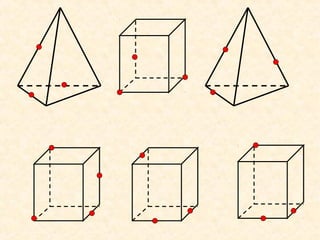
Документ представляет собой план урока по геометрии, посвященный секущим плоскостям и их сечениям на примере тетраэдров и параллелепипедов. Урок включает задачи на построение сечений, правила соединения точек на гранях и примеры получения различных фигур (четырехугольников, треугольников и шестиугольников) в результате пересечения с плоскостями. В документе также описываются конкретные этапы построения сечений для разных геометрических фигур.

1. Тема урока:Тема урока:
.

2. План урока:План урока:
1) Секущая плоскость.
2) Сечения тетраэдра.
3) Сечения параллелепипеда.
5) Задачи №1,2,3.
4) Правила построения сечений.

3. Под сечением будем понимать любую
плоскость(назовем ее секущей плоскостью),по обе
стороны от которой имеются точки данной
фигуры(то есть тетраэдра или параллелепипеда).
Многоугольник, который будет образован этими
отрезками, и является сечением фигуры.
Секущая плоскость пересекает грани по отрезкам.

4. Правила построения
сечений.
1) Секущая плоскость пересекает грани по отрезкам.
2) Соединять отрезками можно только точки,
лежащие на одной грани.
3) Секущая плоскость пересекает противоположные
грани параллелепипеда по параллельным отрезкам.
4) Если точки не лежат в одной грани, то необходимо
построить точки пересечения секущей плоскости с
ребрами, после чего провести отрезки,соединяющие
две построенные точки, лежащие в одной грани.

7. На ребрах АВ,ВД и СД тетраэдра
АВСД отмечены точки М,N и Р.
Построить сечение тетраэдра
плоскостью МNР.
N
м
Р
А
В С
Д
Е
Q
1) Провести отрезок МN.
2) Провести отрезок NР.
3) Найти точку
пересечения
прямых NР и ВС ( т.Е ).
4) Найти точку пересечения
прямых ЕМ и АС ( т.Q ).
5) Провести отрезок PQ.
Четырехугольник МNРQ-
-искомое сечение.

8. N
м
р
А
в С
Д
На ребрах АВ,ВД и С тетраэдра
АВСД отмечены точки М,N и
Р.Построить сечение тетраэдра
плоскостью МNР.
Прямые NР и ВС параллельны.
1) Провести отрезок MN.
2) Провести отрезок NР.
3) Провести отрезок МК
параллельно отрезку NР.
К
4) Провести отрезок РК.
Трапеция МNРК – искомое
сечение.

9. Точка М лежит на боковой грани
АД тетраэдра ДАВС. Построить
сечение тетраэдра плоскостью,
проходящей через точку М
параллельно основанию
АВС.
А
в С
Д
М
Q
Р
R
1) Провести через точку М
отрезок QР, параллельный
отрезку АВ.
2) Провести через точку Р
отрезок РR, параллельный
отрезку АС.
Треугольник QPR-
-искомое сечение.
3) Провести отрезок QR .

10. На ребрах параллелепипеда даны
три точки А, В, С. Построить
сечение плоскостью АВС.
№1 Точки А, В, С лежат на ребрах,
выходящих из одной вершины.
А
В
С
1) Провести отрезок АВ.
2) Провести отрезок ВС.
3) Провести отрезок АС.
Треугольник АВС – искомое сечение.

11. На ребрах параллелепипеда даны
три точки А, В, С. Построить
сечение плоскостью АВС.
А
В
С
№2 Точки расположены на параллельных ребрах.
Д
1) Провести отрезок АВ.
2) Провести отрезок ВС.
3)Провести отрезок СД
параллельно отрезку АВ.
Пятиугольник АВСДЕ - искомое сечение.
Е
4) Провести отрезок АЕ
параллельно отрезку ВС.
5) Провести отрезок ЕД.

12. На ребрах параллелепипеда даны
три точки А, В, С. Построить
сечение плоскостью АВС.
А
В
С
М
F
Е
1)Провести отрезок АВ.
2) Провести отрезок ВС.
а
3) Найти точку пересечения
прямой а и прямой АВ(т. М).
4) В плоскости нижнего
основания провести
прямую, проходящую через
т.М, параллельно прямой
ВС. Отметить точки F и Е.
5) Провести отрезок ДЕ,
параллельно отрезку АВ.
Д
6) Провести отрезок СД.
Шестиугольник АВСДЕF – искомое сечение.