Recommended
PPT
การวิเคราะห์อัลกอริทึม(algorithm analysis)
PDF
ม.1 เตรียมความพร้อมการให้เหตุผล
DOC
การวัดตำแหน่งที่และการกระจาย
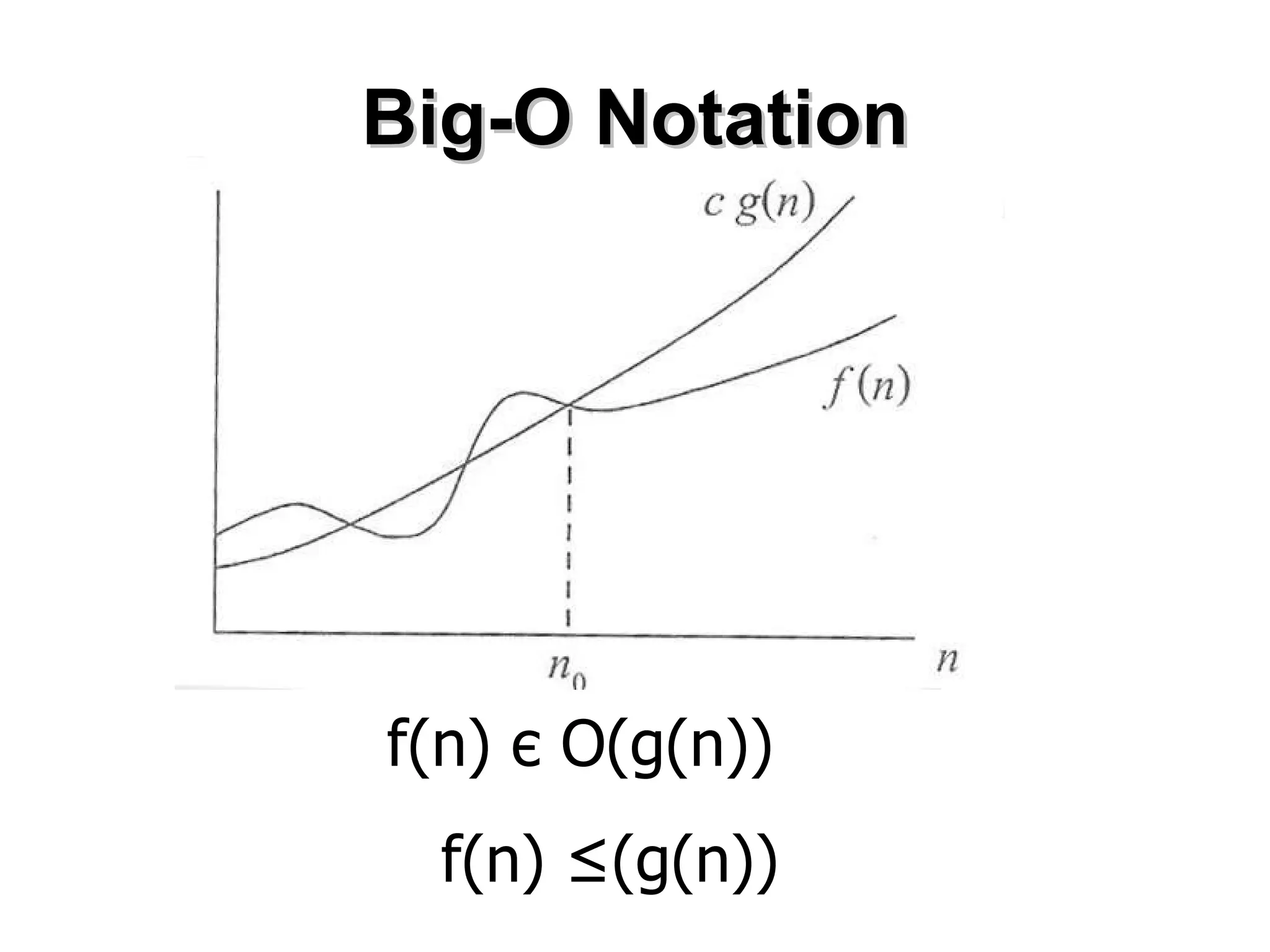
PDF
PDF
อัลกอริทึมและการวิเคราะห์ปัญหา
PDF
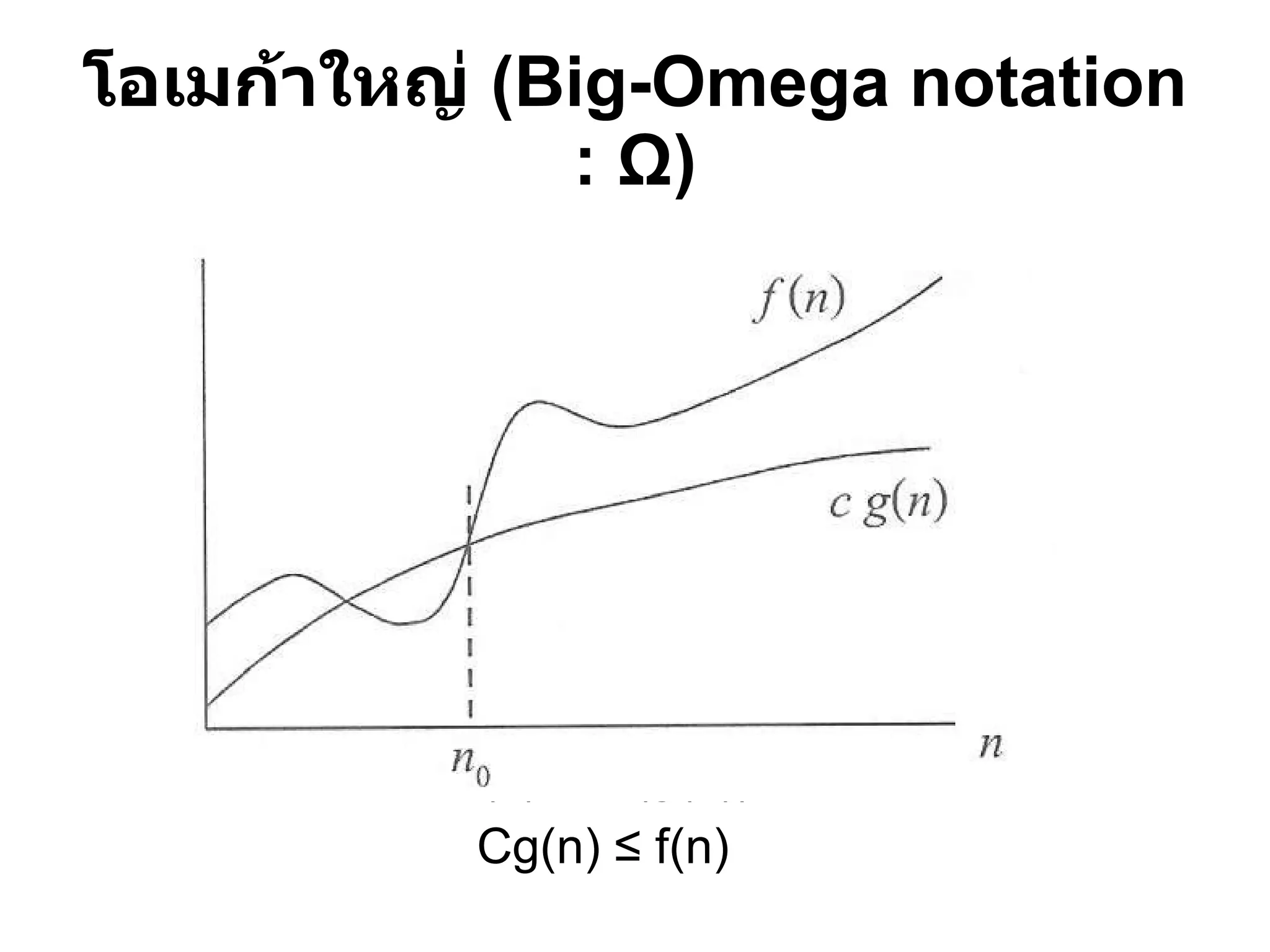
การพัฒนาทักษะกระบวนการทางคณิตศาสตร์
PDF
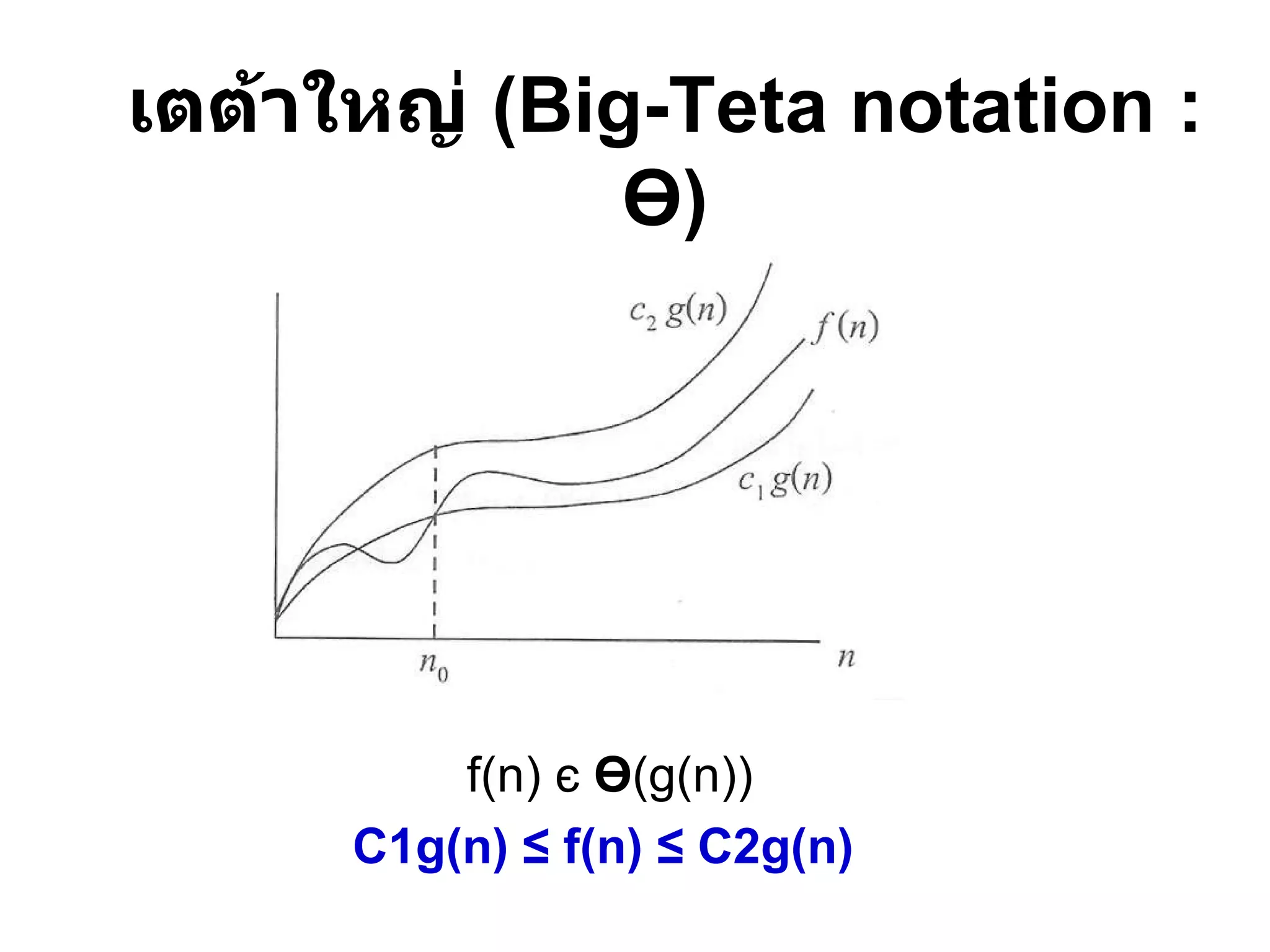
เอกสารประกอบการเรียน เรื่องแผนภูมิวงกลม
PDF
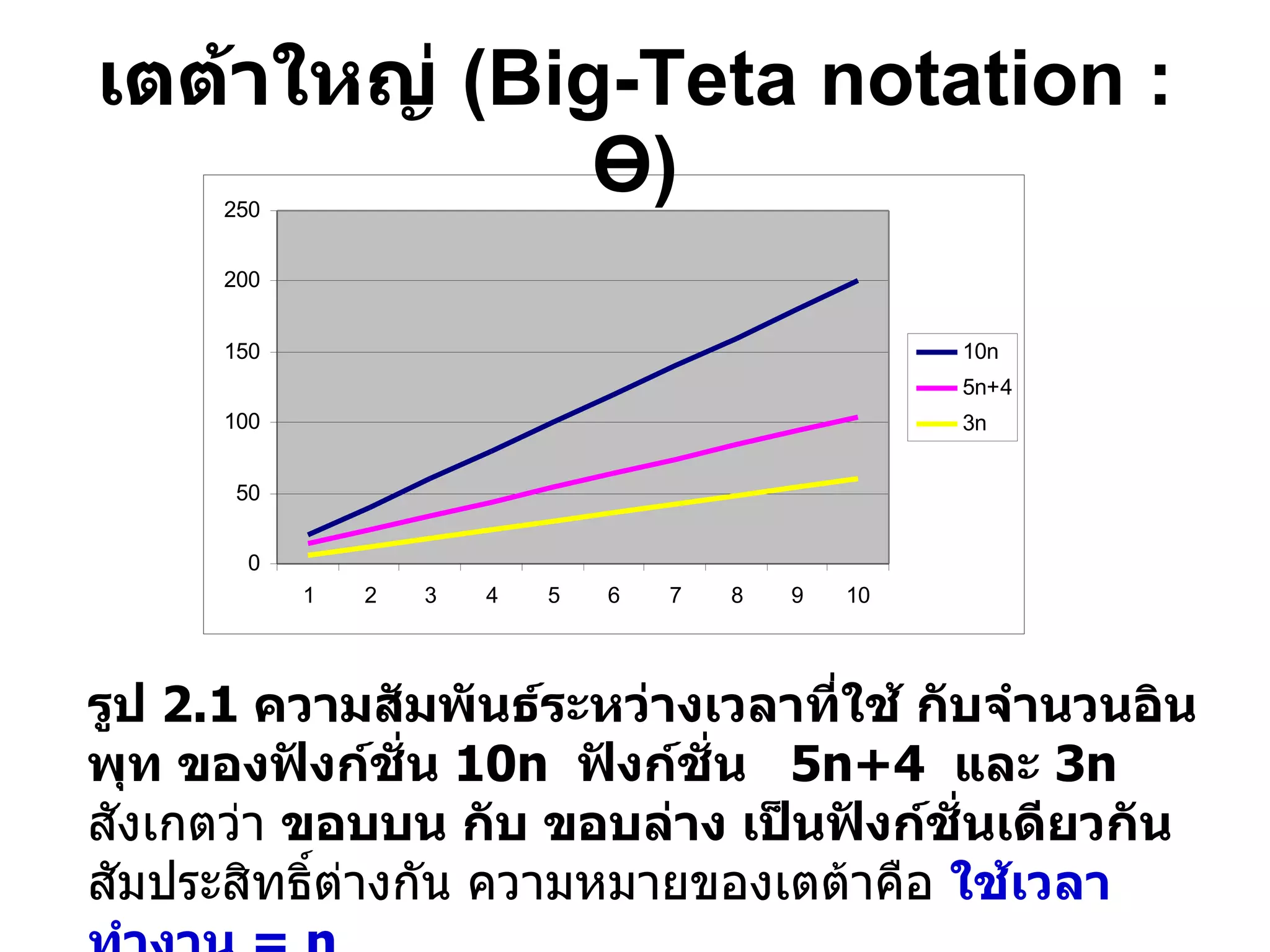
DOCX
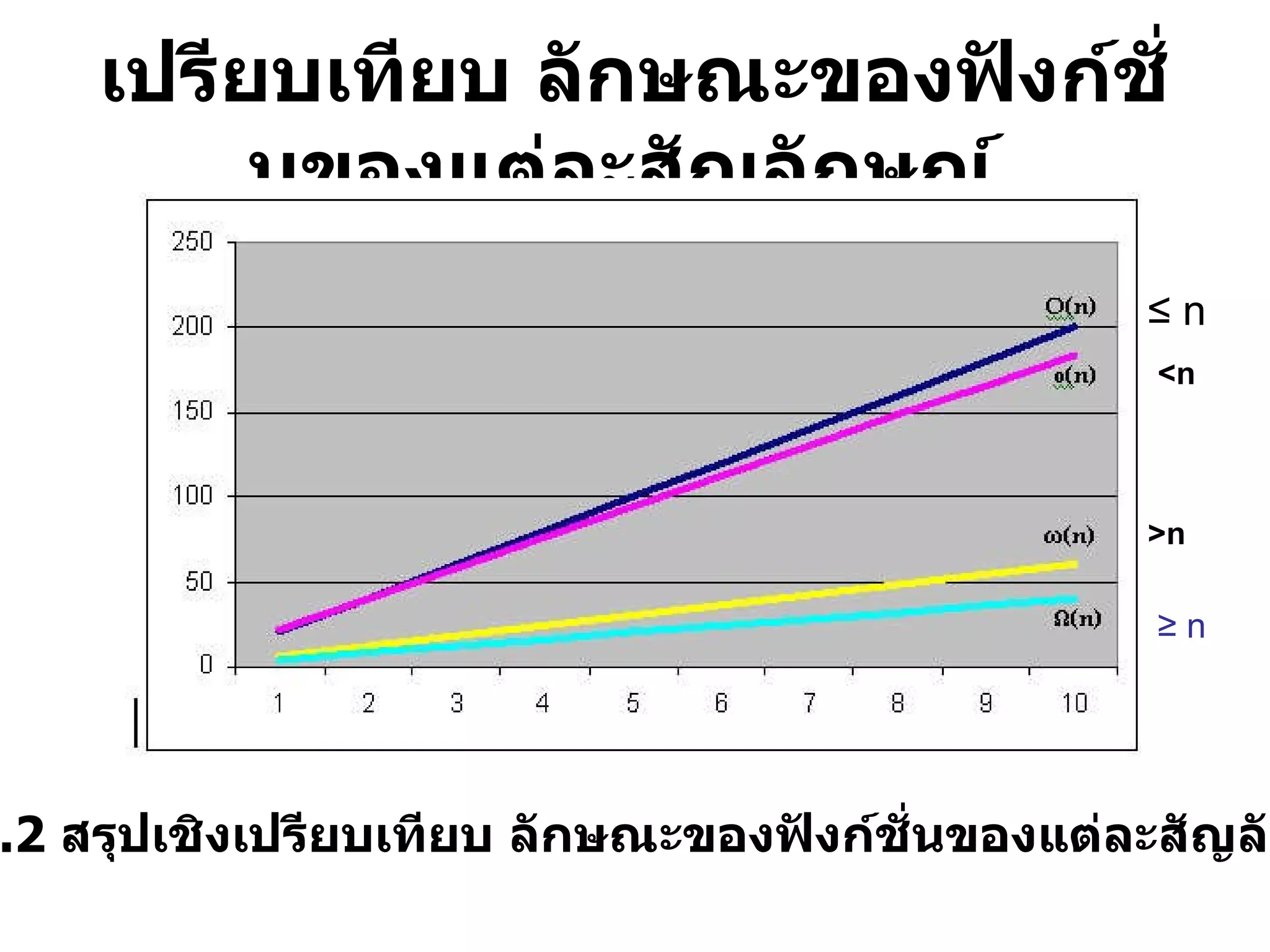
PDF
PDF
PDF
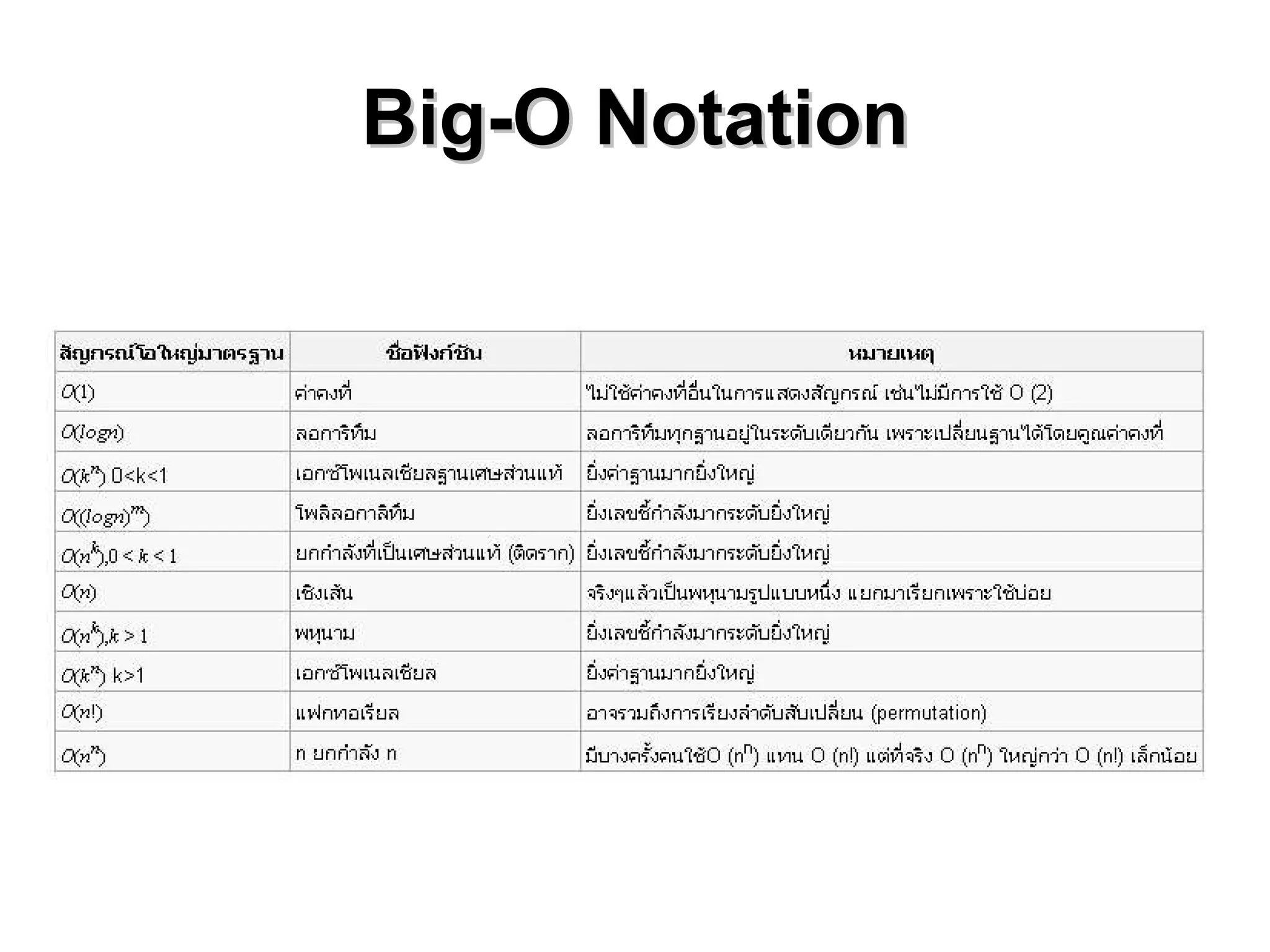
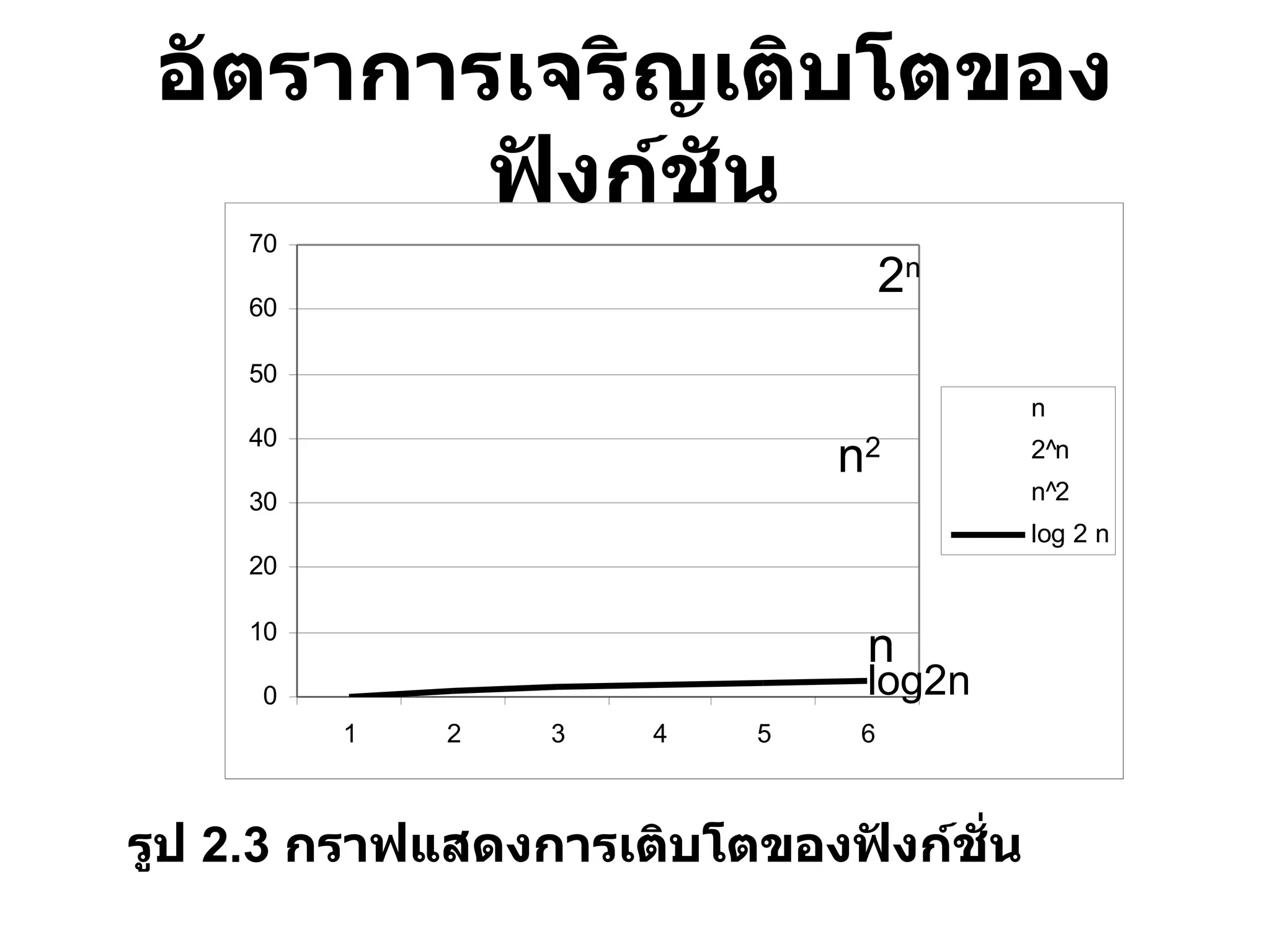
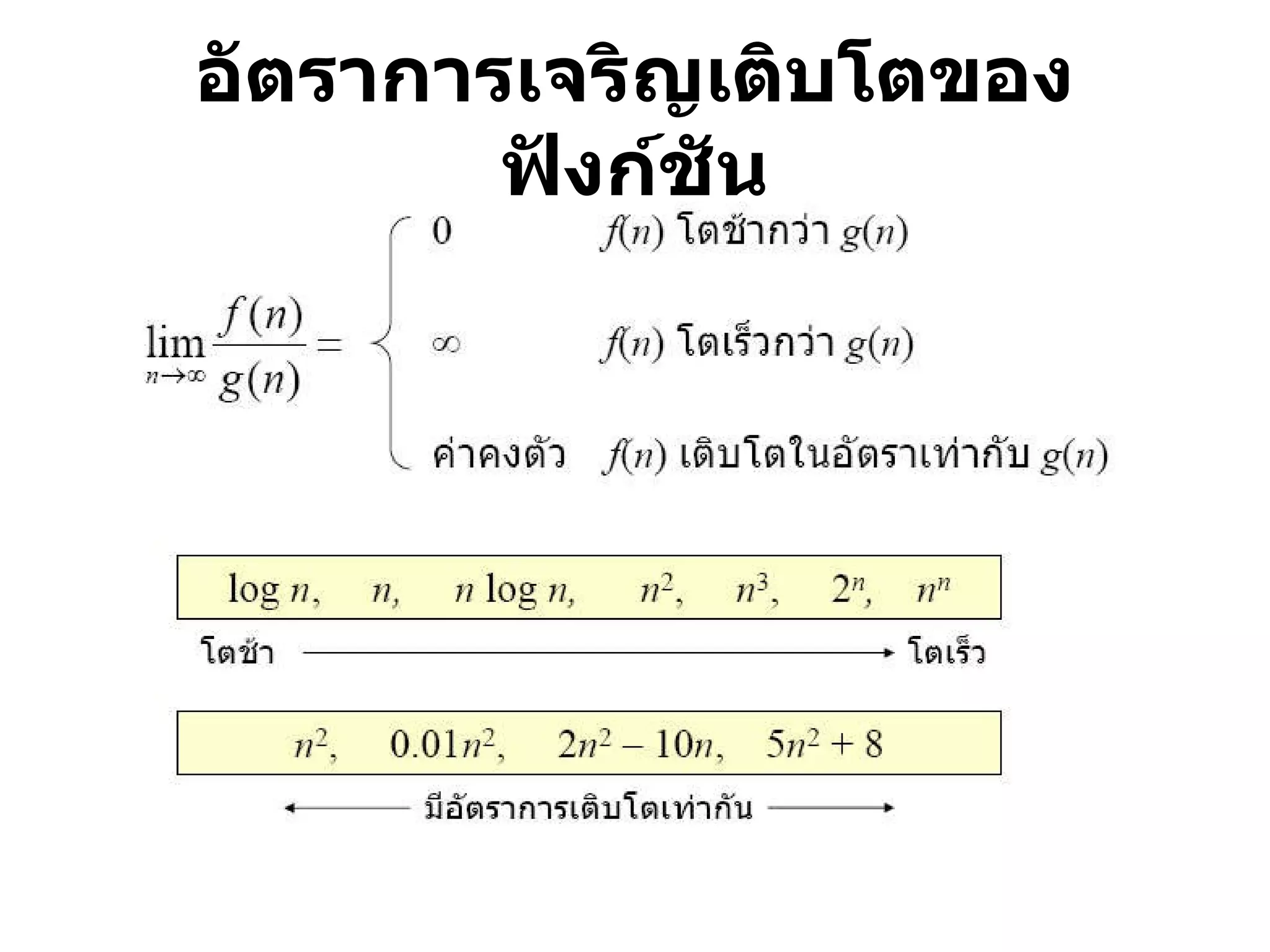
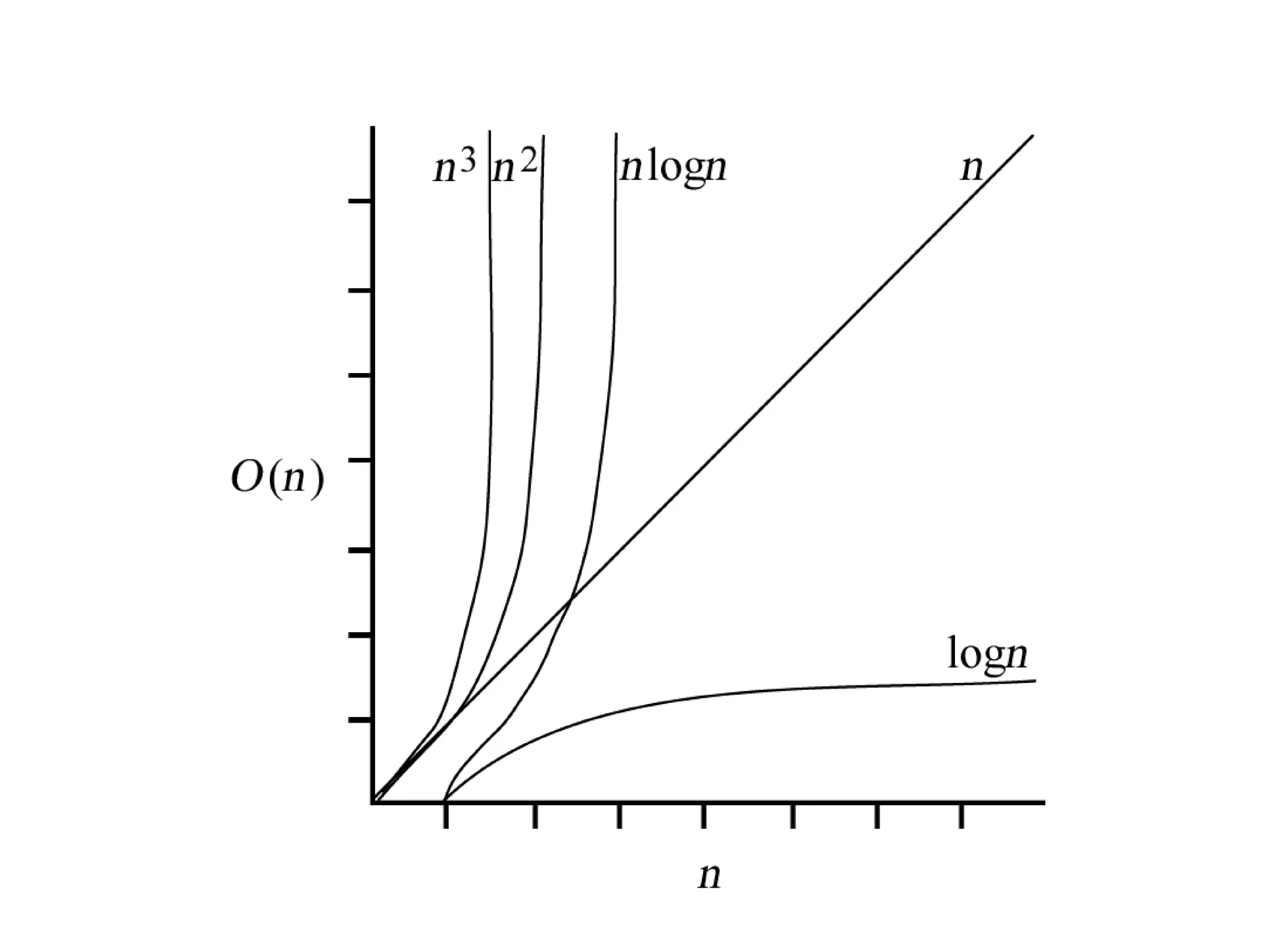
ฟังก์ชันต่อเนื่อง (continuous function)
PDF
การคูณและการหารเลขยกกำลัง
PDF
บทที่ 2 ระบบต่างๆในร่างกายมนุษย์ หมุนเวียนเลือด
PDF
PDF
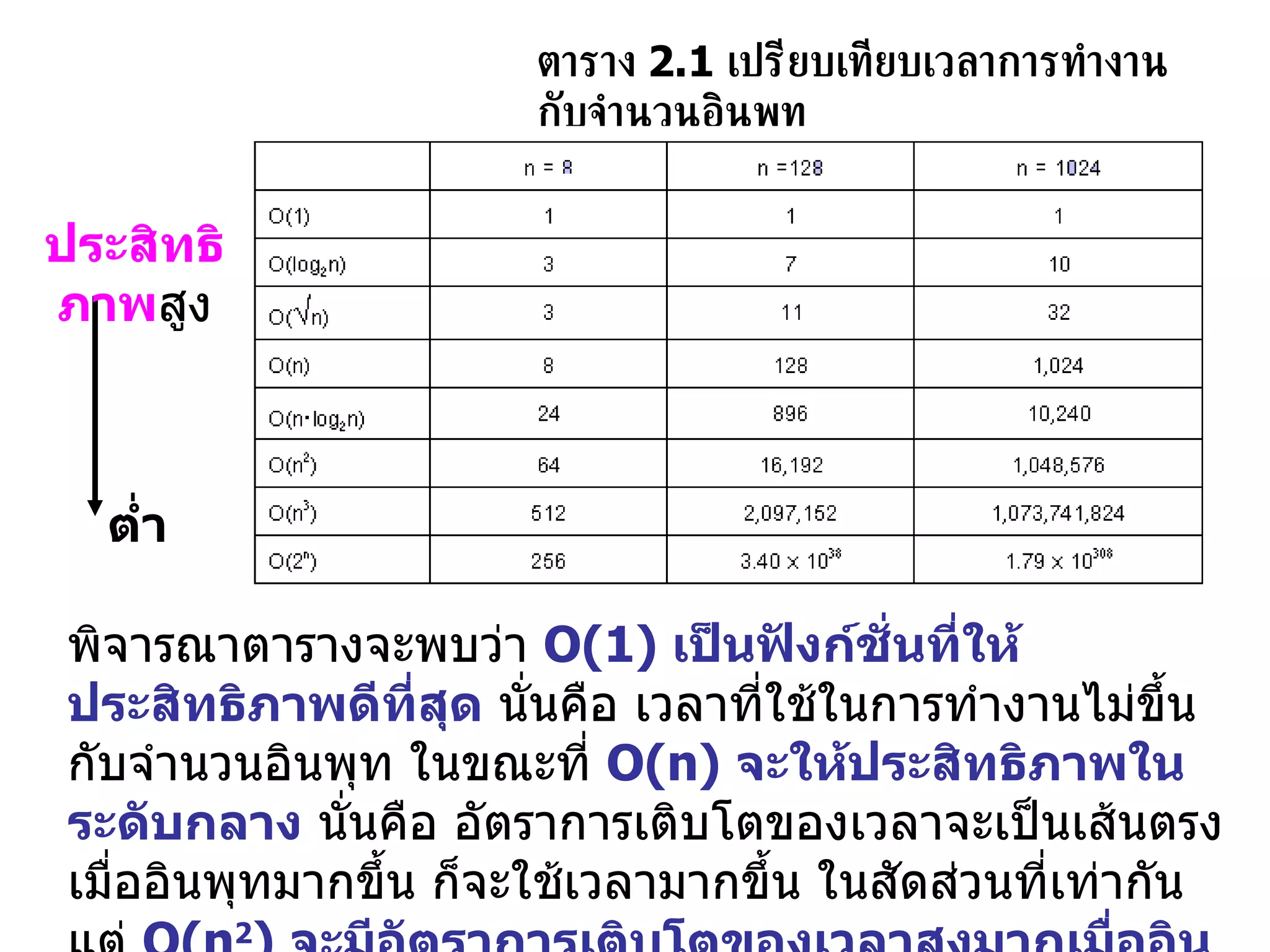
PDF
PDF
หน่วยที่ 3-ระบบทางเทคโนโลยี
PDF
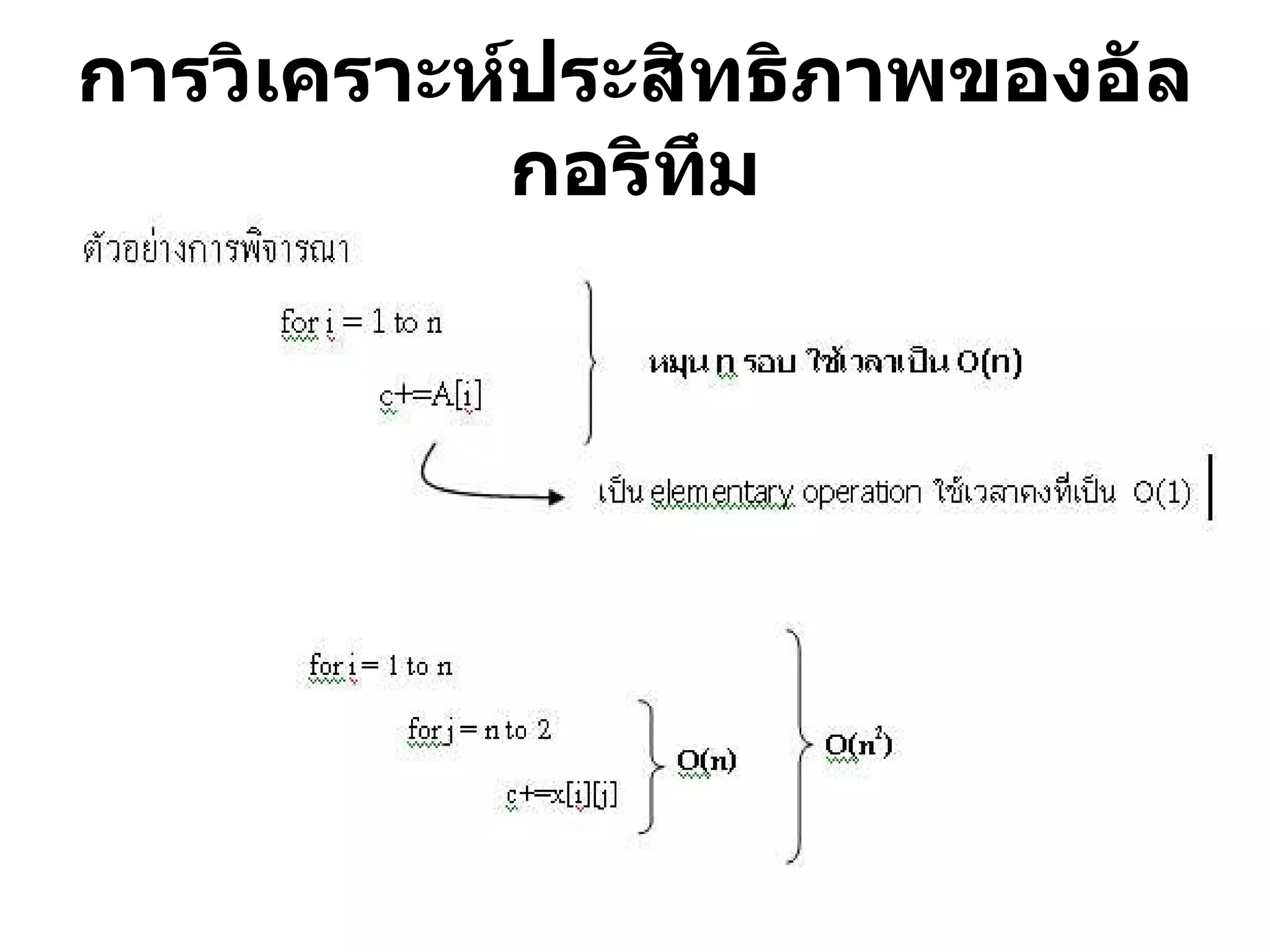
แบบฝึกทักษะเรื่องสถิติ O net
PDF
ใบความรู้ เรื่อง การทำนายรูปร่างโมเลกุลโคเวเลนต์
PPT
PDF
วิทย์ ม.2 บทที่ 5 งาน กำลัง และเครื่องกลอย่างง่าย (คาน รอก พื้นเอียง ลิ่ม ล้อ...
PDF
PDF
PPTX
ความรู้เบื้องต้นเกี่ยวกับการใช้คอมพิวเตอร์และระบบสารสนเทศเพื่องานอาชีพ
PDF
PDF
PPTX
บทที่ 1 แนวคิดทั่วไปเกี่ยวกับฐานข้อมูล
PPT
การจัดเรียงข้อมูล (sorting)
PPT
สแตกและคิว (Stack & queue)
More Related Content
PPT
การวิเคราะห์อัลกอริทึม(algorithm analysis)
PDF
ม.1 เตรียมความพร้อมการให้เหตุผล
DOC
การวัดตำแหน่งที่และการกระจาย
PDF
PDF
อัลกอริทึมและการวิเคราะห์ปัญหา
PDF
การพัฒนาทักษะกระบวนการทางคณิตศาสตร์
PDF
เอกสารประกอบการเรียน เรื่องแผนภูมิวงกลม
PDF
What's hot
DOCX
PDF
PDF
PDF
ฟังก์ชันต่อเนื่อง (continuous function)
PDF
การคูณและการหารเลขยกกำลัง
PDF
บทที่ 2 ระบบต่างๆในร่างกายมนุษย์ หมุนเวียนเลือด
PDF
PDF
PDF
PDF
หน่วยที่ 3-ระบบทางเทคโนโลยี
PDF
แบบฝึกทักษะเรื่องสถิติ O net
PDF
ใบความรู้ เรื่อง การทำนายรูปร่างโมเลกุลโคเวเลนต์
PPT
PDF
วิทย์ ม.2 บทที่ 5 งาน กำลัง และเครื่องกลอย่างง่าย (คาน รอก พื้นเอียง ลิ่ม ล้อ...
PDF
PDF
PPTX
ความรู้เบื้องต้นเกี่ยวกับการใช้คอมพิวเตอร์และระบบสารสนเทศเพื่องานอาชีพ
PDF
PDF
PPTX
บทที่ 1 แนวคิดทั่วไปเกี่ยวกับฐานข้อมูล
Viewers also liked
PPT
การจัดเรียงข้อมูล (sorting)
PPT
สแตกและคิว (Stack & queue)
PPT
อัลกอริทึมและการวิเคราะห์ปัญหา
PPT
PPT
การค้นหาข้อมูล (searching)
PPTX
การเรียงข้อมูลแบบMerge sort นันทนา เนื่องมัจฉา
PPT
โครงสร้างข้อมูลแบบลิงค์ลิสต์ (linklist)
PPTX
ความรู้เบื้องต้นเกี่ยวกับอัลกอริทึม
PPT
PPTX
PDF
Data Structures & Algorithm design using C
PDF
PPT
PPT
บทที่2 โครงสร้างข้อมูลอาร์เรย์
DOC
PDF
PDF
12 การให้เหตุผลและตรรกศาสตร์ สื่อปฏิสัมพันธ์เรื่องตารางค่าความจริง
PDF
PPTX
PDF
Similar to การวิเคราะห์อัลกอริทึม
PPT
PPT
PDF
PDF
PDF
โปรแกรมย่อยและฟังก์ชันมาตรฐาน
PDF
PDF
PDF
PDF
PPT
PDF
PDF
PDF
PDF
PPTX
บทที่4การกำหนดและวิเคราะห์ปัญหา
PPT
PDF
PDF
โจทย์ปัญหา Pbl 4.2 เรื่อง การเขียนอัลกอริทึมแบบโฟลวชาร์ต
PPTX
PPTX
การแก้ปัญหาด้วยกระบวนการเทคโนโลยีสารสนเทศ
การวิเคราะห์อัลกอริทึม 1. 2. 3. 4. 5. Big-O Notation เครื่องหมาย บิ๊ก - โอ ใช้ในการระบุทรัพยากรที่ใช้ในการทำงานของอัลกอริทึมเมื่อขนาดของอินพุทเปลี่ยนไป ปกติแล้วทรัพยากรดังกล่าวจะหมายถึงเวลา นั่นคือ ความสัมพันธ์ระหว่าง เวลา กับ ขนาดของอินพุท อาจกล่าวง่าย ๆ ว่า หากอินพุทมีขนาดใดขนาดหนึ่ง เวลาที่ใช้ในการทำงานมากที่สุด ( upper bound) จะเป็นเท่าใด บิ๊ก - โอ เป็นฟังก์ชั่นที่นิยมใช้มากที่สุดในการระบุประสิทธิภาพของอัลกอริทึม 6. ตัวอย่าง ความหมายของ O(n) คือ ฟังก์ชั่นนั้น ๆ ใช้เวลาทำงานช้าที่สุด ≤ n เช่น อัลกอริทึม a1 มีประสิทธิภาพเป็น O(n 2 ) ถ้า n = 10 แล้ว a1 จะใช้ เวลาทำงานช้าที่สุด 100 หน่วยเวลา ( รับประกันว่าไม่ช้าไปกว่านี้ - แต่อาจจะเร็วกว่านี้ได้ ) Big-O Notation 7. เขียนได้ว่า f(n) є O(g(n)) เพื่อบอกว่า f(n) เป็น ฟังก์ชันที่ไม่โตเร็วกว่า g(n) เราสามารถหาค่าคงตัวบวก C ที่ f(n) ≤ Cg(n) 8. 9. 10. โอเมก้าใหญ่ (Big-Omega notation : Ω ) โอเมก้าใหญ่ จะใช้สำหรับบอกถึง เวลาที่ใช้น้อยที่สุด (lower bound) เมื่ออัลกอริทึมนั้น ๆ ทำงานกับอินพุทขนาดใดขนาดหนึ่ง ตัวอย่าง ความหมายของ Ω (n) คือ ฟังก์ชั่นนั้น ๆ ใช้เวลาทำงานเร็วที่สุด ≥ n เช่น อัลกอริทึม a1 มีประสิทธิภาพเป็น Ω (n) ถ้า n = 10 แล้ว a1 จะใช้เวลา ทำงานเร็วที่สุด 10 หน่วยเวลา ( รับประกันว่า ไม่เร็วไปกว่านี้ - แต่อาจจะช้ากว่านี้ได้ ) 11. เขียนได้ว่า f(n) є Ω (g(n)) เพื่อบอกว่า f(n) เป็น ฟังก์ชันที่ไม่โตไม่ช้ากว่า g(n) เราสามารถหาค่าคงตัวบวก C ที่ Cg(n) ≤ f(n) โอเมก้าใหญ่ (Big-Omega notation : Ω ) 12. 13. เตต้าใหญ่ (Big-Teta notation : Ө ) f(n) = Ө (g(n)) ก็ต่อเมื่อ f(n) = O(g(n)) และ f(n) = Ω (g(n)) นั่นคือ ขอบบนและขอบล่างเป็นฟังก์ชั่นเดียวกัน 14. 15. เตต้าใหญ่ (Big-Teta notation : Ө ) รูป 2.1 ความสัมพันธ์ระหว่างเวลาที่ใช้ กับจำนวนอินพุท ของฟังก์ชั่น 10n ฟังก์ชั่น 5n+4 และ 3n สังเกตว่า ขอบบน กับ ขอบล่าง เป็นฟังก์ชั่นเดียวกัน สัมประสิทธิ์ต่างกัน ความหมายของเตต้าคือ ใช้เวลาทำงาน = n 16. โอเล็ก (Little-o : o) Little-o คือฟังก์ชั่นที่ไม่แตะขอบบน นั่นคือ ฟังก์ชั่นนี้ ทำงานช้าที่สุด < n คือ o(g(n)) คือเซตของฟังก์ชันที่โตช้ากว่า g(n) เช่น หากเรามี t(n) = n0.98 + 0.05√n เราสามารถเขียนได้เป็น O(n) หรือ o(n) แต่หากระบุเป็น Little-o จะเน้นให้เห็นชัดว่าไม่ถึง n ( เพราะค่ากำลังของ n คือ 1 แต่ในฟังก์ชั่น t(n) ค่ากำลังของ n คือ 0.98) 17. โอเมก้าเล็ก (Little-omega : ω ) Little-omega คือฟังก์ชั่นที่ ไม่แตะขอบล่าง นั่นคือ ฟังก์ชั่นนี้ ทำงานเร็วที่สุด > n คือ ω (g(n)) คือเซตของฟังก์ชันที่ โตเร็วกว่า g(n) 18. 19. การหาเทอมที่โตเร็วที่สุดในฟังก์ชั่น คือ อัตราการเจริญเติบโตของฟังก์ชัน ที่แทนประสิทธิภาพของอัลกอริทึม รูปแบบของฟังก์ชั่นที่มักพบบ่อยได้แก่ exponential อยู่ในรูป a n polynomial อยู่ในรูป n a (n ยกกำลังค่าคงที่ ) เช่น n 3 Linear อยู่ในรูป n logarithmic อยู่ในรูป log a n ทั้ง 4 รูปแบบ จะมีอัตราการเติบโตเรียงจากมากไปหาน้อย a n > n a > n > log a n 20. 21. 22. 23. 24. 25. ตย 2 จงเปรียบเทียบอัตราการเจริญเติบโตของ n 10 , 2 n จะได้ว่า n 10 < 2 n อัตราการเจริญเติบโตของฟังก์ชัน 26. ตาราง 2.1 เปรียบเทียบเวลาการทำงานกับจำนวนอินพุท พิจารณาตารางจะพบว่า O(1) เป็นฟังก์ชั่นที่ให้ประสิทธิภาพดีที่สุด นั่นคือ เวลาที่ใช้ในการทำงานไม่ขึ้นกับจำนวนอินพุท ในขณะที่ O(n) จะให้ประสิทธิภาพในระดับกลาง นั่นคือ อัตราการเติบโตของเวลาจะเป็นเส้นตรง เมื่ออินพุทมากขึ้น ก็จะใช้เวลามากขึ้น ในสัดส่วนที่เท่ากัน แต่ O(n 2 ) จะมีอัตราการเติบโตของเวลาสูงมากเมื่ออินพุทมีขนาดใหญ่ขึ้น จากตาราง ประสิทธิภาพจะเรียงลำดับจากสูงไปหาต่ำ ประสิทธิภาพ สูง ต่ำ 27. 28. 29. 30. ตย . อัลกอริทึม 3 Sum := (1+n)*n/2; การวิเคราะห์ประสิทธิภาพของอัลกอริทึม f(n) = O(1) 31. 32. การหาค่า Big-Oh หาได้โดยนำ f(n) มากระทำดังนี้ 1. ตัดสัมประสิทธิ์ของแต่ละเทอมทิ้ง 2. เลือกเทอมที่ใหญ่สุดเก็บไว้เป็นคำตอบ ตัวอย่างเช่น f(n) = 3n 4 + 2n 2 + n n 4 + n 2 + n n 4 O(f(n)) = 33. เมื่อพิจารณาจาก f(n) จะพบว่า อัลกอริทึม 1 f(n) = n อัลกอริทึม 2 f(n) = n-1 อัลกอริทึม 3 f(n) = 1 ประสิทธิภาพ ต่ำสุด ประสิทธิภาพ ดีสุด 34. การหาค่า Big-Oh ตย จงหาค่า Big-o ของ n 3 +2n 3 +10 1. ตัดสัมประสิทธิ์ของแต่ละเทอมทิ้ง จะได้ n 3 +n 3 2. เลือกเทอมที่ใหญ่สุดเก็บไว้เป็นคำตอบ O(f(n)) = O ( n 3 ) 35. การหาค่า Big-Oh ตย จงหาค่า Big-o ของ 100 F(n) = 100 O(f(n)) = O( 1 ) ตย จงหาค่า Big-o ของ 100N+1 F(n) = 100N+1 O(f(n)) = O( N ) 36. การหาค่า Big-Oh ตย จงหาค่า Big-o ของ 20nlogn+5n = O(nlogn) F(n) = 20nlogn+5n F(n) = nlogn+n O(f(n)) = = O(nlogn) 37. สมมติให้แต่ละโปรแกรมใช้เวลาในการทำงานเป็นดังนี้ prg1 = 3n 2 +2n prg2 = 2log 2 n+6n+n prg3 = n+nlog 2 n+4n+9 จงแสดง Big-O ของแต่ละโปรแกรมพร้อมทั้งเรียงลำดับประสิทธิภาพของโปรแกรมจากดีสุดไปหาช้าสุด 2Log 2 n < nlog 2 n < 3n 2 จะได้ 1. prg2 2. prg3 3.prg1 การวิเคราะห์ประสิทธิภาพของอัลกอริทึม