More Related Content
What's hot
What's hot (20)
Similar to ラビットチャレンジレポート 機械学習
Similar to ラビットチャレンジレポート 機械学習 (20)
ラビットチャレンジレポート 機械学習
- 2. 目次 線形回帰モデル 非線形回帰モデル ロジスティック回帰モデル 主成分分析 サポートベクターマシン 2
- 3. 線形回帰モデル 3
- 4. 線形回帰モデル 4 概要 線形回帰モデル: 回帰問題を解くための教師あり機械学習モデルの一種。説明変数(特徴量)の線形結合を出力(目的 変数)とし、各変数の係数を学習パラメータとするモデル。 回帰問題: 連続値や離散値の入力に対し、連続値を出力とした問題。 教師あり学習: 学習データに正解データも含まれた状態で学習する手法。 𝑦 = 𝒘𝑻 𝒙 + 𝑤0 = 𝑗=1 𝑚 𝑤𝑗𝑥𝑗 + 𝑤0 線形回帰モデルの式 𝑤𝑗: 学習パラメータ 𝑥𝑗: 入力変数 𝑦: 予測値 入力変数が１つのみの場合単回帰モデルと呼び、2つ以上の場合重回帰モデルと呼ぶ。
- 5. 線形回帰モデル 5 パラメータの推定方法 最小二乗法: 実測値と予測値の差(残差) の二乗和が最小となるパラメータで推定する方法。 最尤法: 誤差がある確率分布に従う確率変数と仮定し、その尤度関数を最大にするパラメータで推定する方法。 誤差が独立に正規分布に従うと仮定した場合、最尤法の結果と最小二乗法の結果は一致する。 𝐿𝑜𝑠𝑠(𝒘) = 𝑗=1 𝑚 (𝑦𝑗 − 𝑦𝑗)2 = 𝑗=1 𝑚 (𝑦𝑗 − 𝒘𝑻 𝒙𝑗 − 𝑤0)2 残差平方和の式 𝑦𝑗: 実測値 𝑦𝑗: 予測値 𝐿 𝒘 = 𝑗=1 𝑚 1 2𝜋𝜎 𝑒 − (𝑦𝑗−𝑦𝑗)2 2𝜎2 = 1 (2𝜋𝜎) 𝑚 2 𝑒 − 𝑗=1 𝑚 (𝑦𝑗−𝒘𝑻𝒙𝑗−𝑤0)2 2𝜎2 尤度関数の式 機械学習の分野では、上式のようなパラメータ推定のために最小化する関数を損失関数や誤差関数と呼ぶ 尤度関数の対数をとると、残差平方和の符号をマイナスにして定数倍したものに定数項を加えたものになる 従って残差平方和を最小化する問題と尤度関数を最大にする問題は等価であることが分かる 𝑙 𝒘 = log𝐿 𝒘 = − 1 2𝜎2 𝑗=1 𝑚 𝑦𝑗 − 𝒘𝑻 𝒙𝑗 − 𝑤0 2 − 𝑚 2 log(2𝜋𝜎) 対数尤度関数の式
- 6. 線形回帰モデル 6 問題: ボストンの住宅データセットを線形回帰モデルで分析 部屋数が4で犯罪率が0.3の物件はいくらになるか予測する 実装(問題設定) 番号 変数名 内容 1 CRIM 犯罪発生率 2 ZN 25000平方メートル以上の住宅区間の割合 3 INDUS 非小売業土地面積の割合 4 CHAS チャールズ川沿いかどうか 5 NOX 窒素酸化物濃度 6 RM 一戸あたりの平均部屋数 7 AGE 1940年よりに前に建てられた家屋の割合 8 DIS ボストンの主な雇用圏までの重み付き距離 9 RAD 幹線道路へのアクセス指数 10 TAX 10000ドルあたりの所得税率 11 PIRATIO 教師あたりの生徒の数 12 B 1000(Bk-0.63)^2で計算される量 13 LSTAT 低所得者の割合 14 MEDV 住宅価格 ボストンの住宅データセットの概要 目的変数
- 7. 線形回帰モデル 7 実装(Jupyter notebook) MEDV = 8.39RM − 0.26CRIM − 29.44 学習したモデルの式 8.39 × 4 − 0.26 × 0.3 − 29.44 = 4.24 部屋数4、犯罪率0.3の物件の予測結果 部屋数4、犯罪率0.3の物件の価格は4,240＄の 物件と予測される
- 8. 非線形回帰モデル 8
- 9. 非線形回帰モデル 9 概要 非線形回帰モデル: 回帰問題を解くための教師あり機械学習モデルの一種。線形回帰モデルとは異なり、曲線で 予測を行う。説明変数(特徴量)を非線形変換したものの線形結合を出力(目的変数)とし、各変数の係数を学習パ ラメータとするモデル。 𝑦 = 𝒘𝑻 𝝓(𝒙) + 𝑤0 = 𝑗=1 𝑚 𝑤𝑗𝜙𝑗(𝑥𝑗) + 𝑤0 非線形回帰モデルの式 𝑤𝑗: 学習パラメータ 𝑥𝑗: 入力変数 𝑦: 予測値 𝜙: 非線形関数 非線形関数に用いられる基底関数 ・多項式関数 ・ガウス型基底関数 ・スプライン関数/Bスプライン関数 学習パラメータはあらかじめ非線形変換を施したデータに対し、線形回帰モデルと同様の方法で推定可能である
- 11. 非線形回帰モデル 11 正則化 正則化: モデルの過学習を抑制するために、損失関数に正則化項(罰則項)を追加する手法。 Lasso回帰: 正則化項として𝐿1ノルムを用いる手法。 Ridge回帰: 正則化項として𝐿2ノルムを用いる手法。 Elastic-Net: 正則化項として𝐿1ノルムと𝐿2ノルムの両方を用いる手法。 𝑅(𝒘) = 𝜆 𝑗=0 𝑚 𝑤𝑗 𝐿1ノルムの式 𝑅(𝒘) = 𝜆 𝑗=0 𝑚 𝑤𝑗 2 𝐿2ノルムの式 𝑅(𝒘) = 𝜆 𝛼 𝑗=0 𝑚 𝑤𝑗 + (1 − 𝛼) 𝑗=0 𝑚 𝑤𝑗 2 Elastic-Netの式 𝜆は正の値で正則化パラメータと呼ばれ罰則の大きさを調整する役割がある 𝛼は𝐿1ノルムと𝐿2ノルムのバランスを調整する役割がある どちらのパラメータも学習前に事前に決めておく必要があり、ハイパーパラメータと呼ばれる
- 12. ロジスティック回帰モデル 12
- 13. ロジスティック回帰モデル 13 概要 ロジスティック回帰モデル: 分類問題を解くための教師あり機械学習モデルの一種。クラス1に分類される確率𝑝を ロジット関数を用いて変換したものを説明変数の線形結合で表す。 分類問題: 連続値や離散値の入力に対し、離散値を出力とした問題。 logit 𝑝 = log 𝑝 1 − 𝑝 ロジット関数の式 𝑤𝑗: 学習パラメータ 𝑥𝑗: 入力変数 𝑝: クラス1になる確率 𝜎(𝑥)のことをシグモイド関数と呼び、学習パラメータ𝑤𝑗は最尤法により推定される 𝑝が0.5以上のときクラス1、0.５未満であればクラス0と予測する(閾値は任意に変更可能) logit 𝑝 = log 𝑝 1 − 𝑝 = 𝒘𝑻𝒙 + 𝑤0 = 𝑗=1 𝑚 𝑤𝑗𝑥𝑗 + 𝑤0 ロジスティック回帰モデルの式 𝑝 = 1 1 + exp{−𝛼(𝒘𝑻𝒙 + 𝑤0)} = 𝜎(𝒘𝑻 𝒙 + 𝑤0) 𝑝について解くと
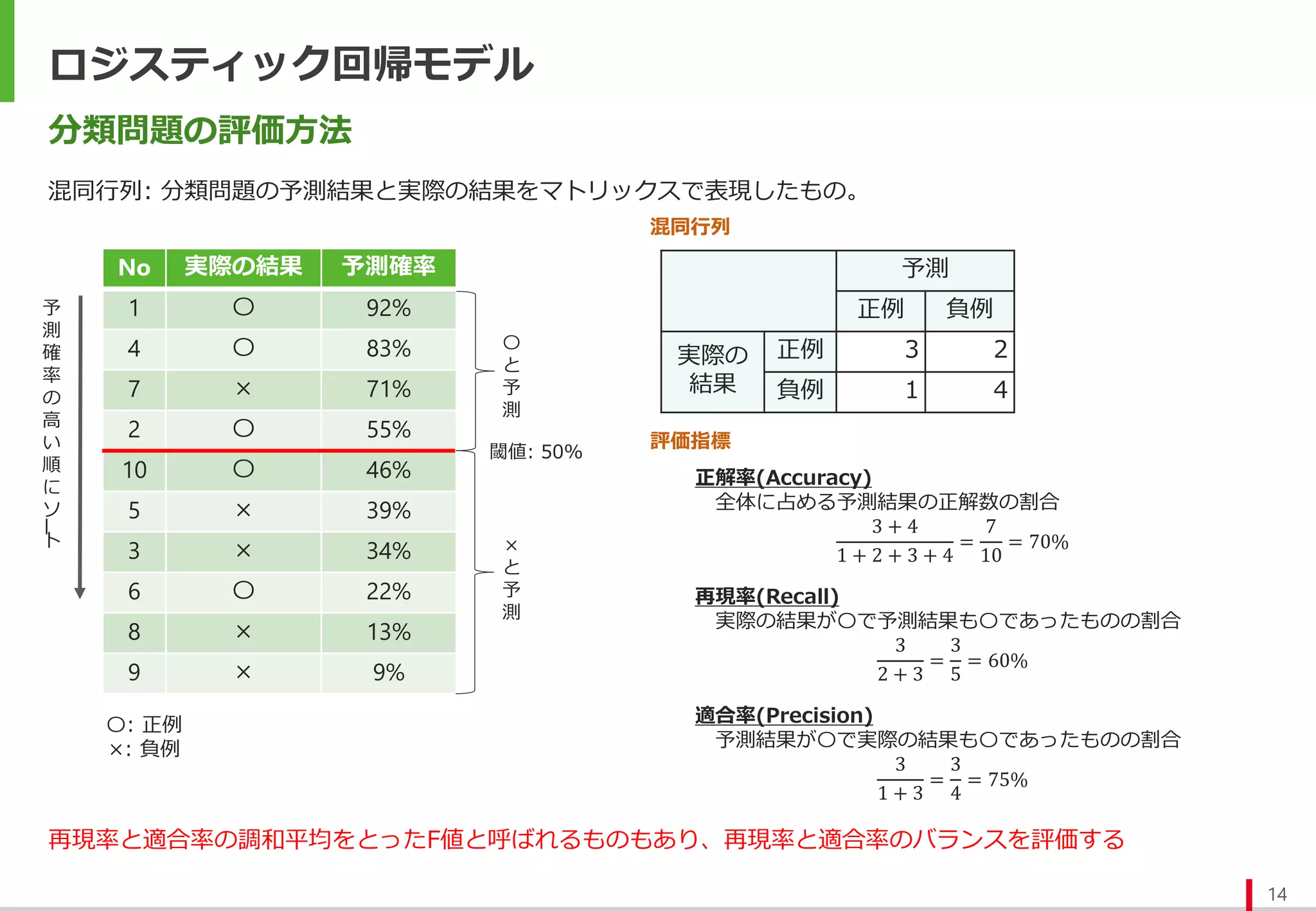
- 14. ロジスティック回帰モデル 14 分類問題の評価方法 混同行列: 分類問題の予測結果と実際の結果をマトリックスで表現したもの。 予測 正例 負例 実際の 結果 正例 3 2 負例 1 4 No 実際の結果 予測確率 1 〇 92% 4 〇 83% 7 × 71% 2 〇 55% 10 〇 46% 5 × 39% 3 × 34% 6 〇 22% 8 × 13% 9 × 9% 予 測 確 率 の 高 い 順 に ソ ー ト 評価指標 〇 と 予 測 × と 予 測 閾値: 50% 〇: 正例 ×: 負例 正解率(Accuracy) 全体に占める予測結果の正解数の割合 3 + 4 1 + 2 + 3 + 4 = 7 10 = 70% 再現率(Recall) 実際の結果が〇で予測結果も〇であったものの割合 3 2 + 3 = 3 5 = 60% 適合率(Precision) 予測結果が〇で実際の結果も〇であったものの割合 3 1 + 3 = 3 4 = 75% 混同行列 再現率と適合率の調和平均をとったF値と呼ばれるものもあり、再現率と適合率のバランスを評価する
- 15. ロジスティック回帰モデル 15 問題: タイタニックの乗客データをロジスティック回帰モデルで分析 年齢が30歳で男の乗客は生き残れるか予測する 実装(問題設定) 番号 変数名 内容 1 PassengerId 乗客ID 2 Survived 生存・死者情報 3 Pclass 乗客の社会階級 4 Name 乗客名 5 Sex 性別 6 Age 年齢 7 SibSp 兄弟及び配偶者の数 8 Parch 親もしくは子供の数 9 Ticket チケットNo 10 Fare 運賃 11 Cabin 船室 12 Embarked 乗船した漁港 タイタニックデータの概要 目的変数
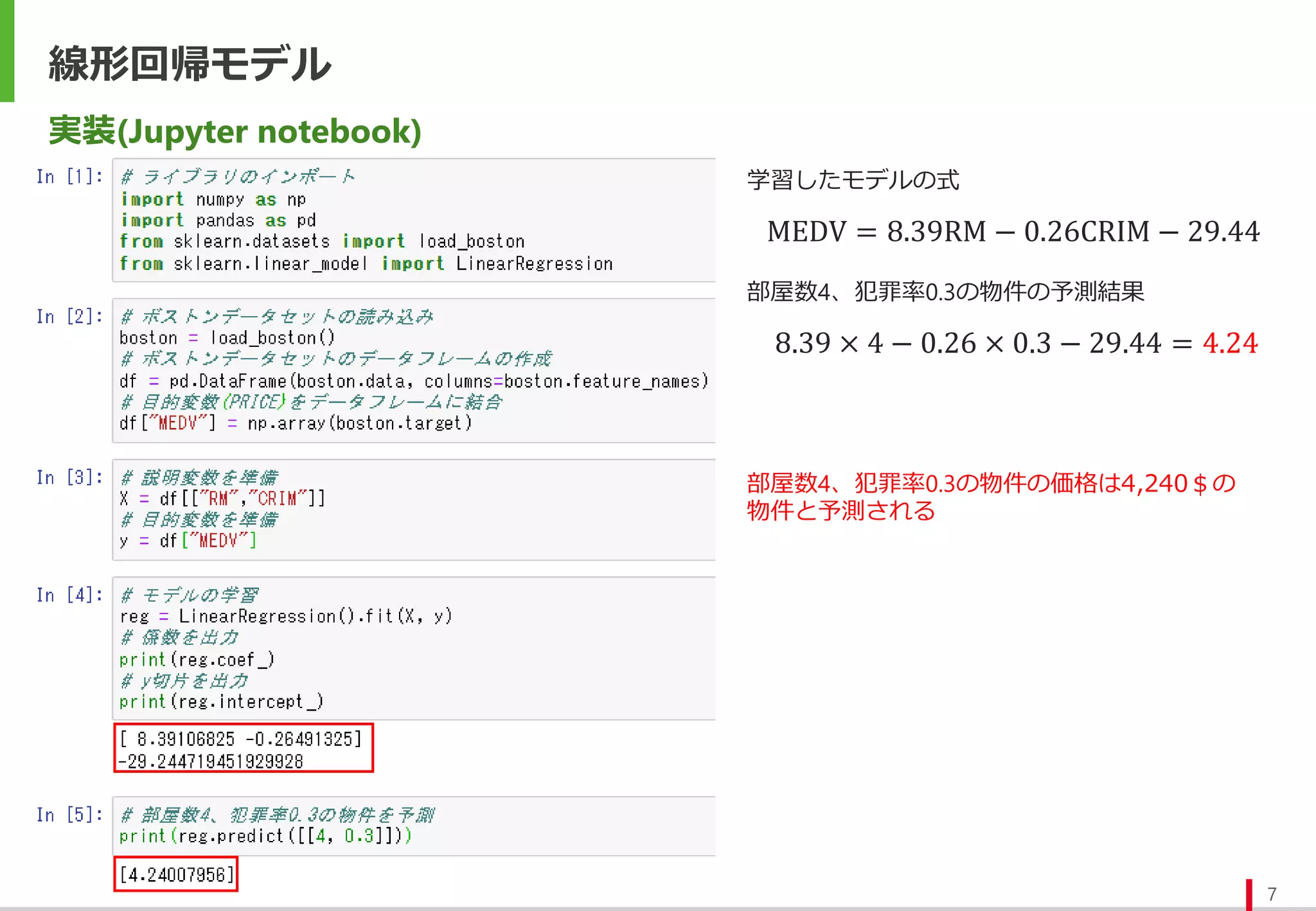
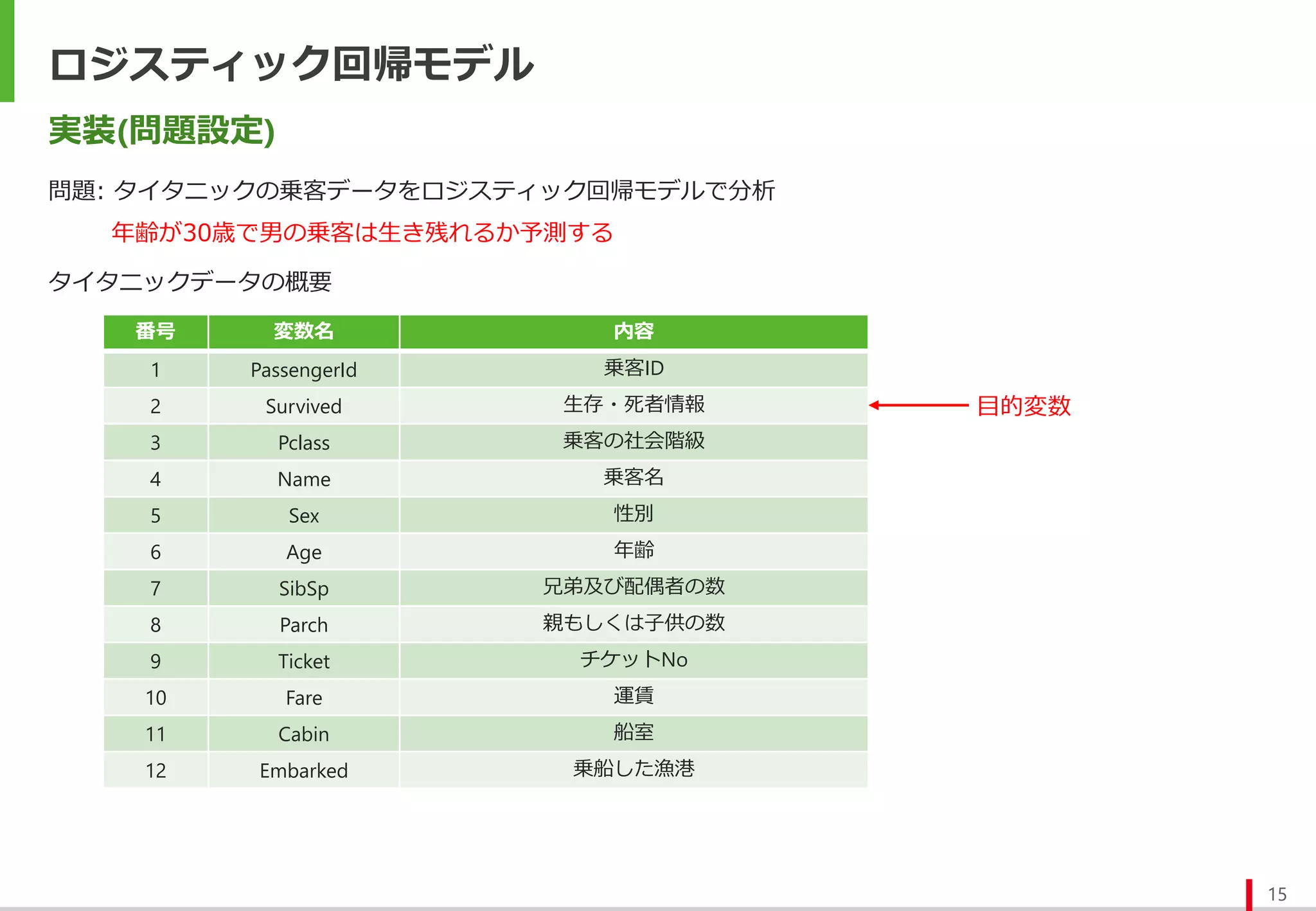
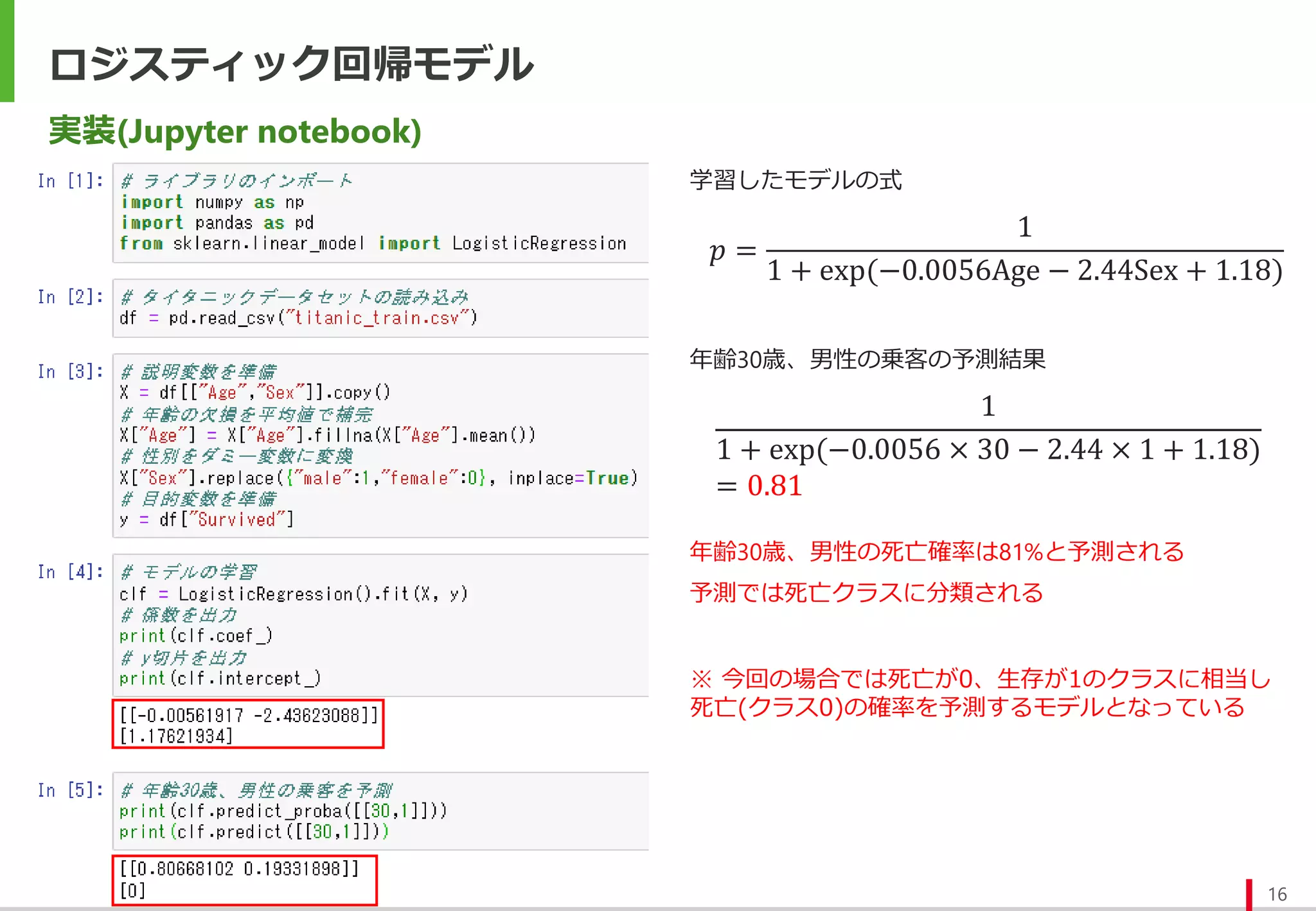
- 16. ロジスティック回帰モデル 16 実装(Jupyter notebook) 𝑝 = 1 1 + exp(−0.0056Age − 2.44Sex + 1.18) 学習したモデルの式 1 1 + exp(−0.0056 × 30 − 2.44 × 1 + 1.18) = 0.81 年齢30歳、男性の乗客の予測結果 年齢30歳、男性の死亡確率は81%と予測される 予測では死亡クラスに分類される ※ 今回の場合では死亡が0、生存が1のクラスに相当し 死亡(クラス0)の確率を予測するモデルとなっている
- 17. 主成分分析 17
- 18. 主成分分析 18 概要 主成分分析: 教師なし学習の一種。多次元データをより少ない次元のデータで表現する次元削減のための手法。 次元削減: 高次元のデータを低次元で表現すること。データ容量の削減や可視化を容易にするために行われる。 教師なし学習: 学習データに正解データが含まれない状態で学習する手法。出力が具体的に決まっていない。 主成分分析の流れ 1. 各変数について平均値を引き、全特徴量の平均値が0のデータ𝑋を求める 2. 標本分散共分散行列 1 𝑛 𝑋𝑇 𝑋を求める 3. 分散共分散行列の固有値、固有ベクトルを求め直行行列で対角化する 4. 平均値を0にしたデータ𝑋を固有ベクトルの線形結合で表現する 5. このときの係数を対応する固有ベクトルの固有値が大きい順に第1主成分、第2主成分・・・と呼ぶ ※ 分散共分散行列は必ず半正定値対象行列であり、直行行列で対角化可能である(応用数学のレポート参照) また固有値は全て0以上となる
- 19. 主成分分析 19 問題: 乳がん検査データを主成分分析で分析 32次元のデータを2次元上に圧縮した際に、うまく判別できるか 実装(問題設定) 項目 内容 データセット名 乳がん検査データ レコード数 569 カラム数 33 乳がん検査データの概要
- 21. サポートベクターマシン 21
- 22. サポートベクターマシン 22 概要 サポートベクターマシン: 分類問題を解くための教師あり機械学習モデルの一種。境界面と最も近いデータとの距離 (マージン)を最大化するパラメータを学習する。分類は判別関数の符号によって行われる。 𝑓 𝒙 = 𝒘𝑻 𝝓 𝒙 + 𝑏 判別関数の式 𝒘, 𝑏: 学習パラメータ 𝑥𝑗: 入力変数 𝜙: 非線形関数 𝑓 𝒙 ≥ 0 → 𝑦 = 1 𝑓 𝒙 < 0 → 𝑦 = −1 分類方法 max 𝒘,𝑏 min 𝑖 𝒘𝑻𝝓 𝒙𝒊 + 𝑏 𝒘 パラメータの推定方法 𝑤𝑇𝜙 𝑥𝑖 +𝑏 𝑤 はデータと超平面𝑓 𝒙 = 0との距離であり、min 𝑖 𝒘𝑻𝝓 𝒙𝒊 +𝑏 𝒘 は最も超平面に近いデータとの距離を表す これを最大にするパラメータを学習するため上式の最適化問題を解けばよいことになる
- 23. サポートベクターマシン 23 問題: タイタニックデータをサポートベクターマシンで分析 年齢が30歳で男の乗客は生き残れるか予測する ロジスティック回帰の結果と比較する 実装(問題設定) 番号 変数名 内容 1 PassengerId 乗客ID 2 Survived 生存・死者情報 3 Pclass 乗客の社会階級 4 Name 乗客名 5 Sex 性別 6 Age 年齢 7 SibSp 兄弟及び配偶者の数 8 Parch 親もしくは子供の数 9 Ticket チケットNo 10 Fare 運賃 11 Cabin 船室 12 Embarked 乗船した漁港 タイタニックデータの概要 目的変数
- 26. サポートベクターマシン 26 ロジスティック回帰との比較(2/2) 予測精度の算出 ロジスティック回帰 SVM 正解率 0.79 0.63 再現率 0.71 0.09 適合率 0.73 0.67 F値 0.72 0.15 全ての指標についてロジスティック回帰の方が優秀 な結果となった 今回はパラメータの探索などは行っていないため、 チューニング次第で精度の向上が期待できる