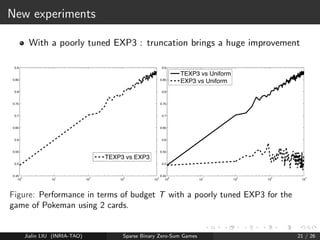
The document discusses sparse binary zero-sum games, focusing on Nash equilibria and their computational strategies. It compares classical linear programming solutions with approximate solutions for efficiency, particularly in games with sparse equilibria. Experimental results demonstrate improvements in performance using truncation methods in certain card games.

1. Sparse Binary Zero-Sum Games
[ACML 2014]
David Auger1 Jialin Liu2 Sylvie Ruette3 David L. St-Pierre4
Olivier Teytaud2
1AlCAAP, Laboratoire PRiSM, Universite de Versailles Saint Quentin-en-Yvelines, France
2TAO, INRIA-CNRS-LRI, Universite Paris-Sud, France
3Laboratoire de Mathematiques, CNRS, Universite Paris-Sud, France
4Universite du Quebec a Trois-Rivieres, Canada
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 1 / 26

2. Thanks to reviewers for very fruitful comments.
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 2 / 26

3. Introduction
Two-person zero-sum game MKK
Nash Equilibrium ! O(K2) with 3
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 3 / 26

4. Introduction
Two-person zero-sum game MKK
Nash Equilibrium ! O(K2) with 3
If the Nash is sparse ! k k submatrix
! O(k3kK log K) with probability 1 (provable)
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 3 / 26

5. Zero-sum matrix games
Game de

6. ned by matrix M
I choose (privately) i
Simultaneously, you choose j
I earn Mi ;j
You earn Mi ;j
So this is zero-sum.
Or you earn 1 Mi ;j (so this is 1-sum, equivalent).
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 4 / 26

7. Ok, I earn Mi ;j , you earn Mi ;j
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 5 / 26

8. Ok, I earn Mi ;j , you earn Mi ;j
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 5 / 26

9. Nash Equilibrium
Nash Equilibrium (NE)
Zero-sum matrix game M
My strategy = probability distrib. on rows = x
Your strategy = probability distrib. on cols = y
Expected reward = xTMy
There exists x; y such that 8x; y,
xTMy xTMy xTMy:
(x; y) is a Nash Equilibrium (no unicity).
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 6 / 26

10. Ok, I earn Mi ;j , you earn Mi ;j
Nash: Ok I play i with probability x
i
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 7 / 26

11. Ok, I earn Mi ;j , you earn Mi ;j
Nash: Ok I play i with probability x
i
How to
compute x*?
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 7 / 26

12. Solving Nash
Solution 1: Linear Programming (LP)
1 M M + C so that it is positive (without loss of generality)
2 LP:

13. nd 0 u minimizing
P
i
ui such that (MT ) u 1
P
3 x = u=
i
ui
=) classical, provably exact, polynomial time
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 8 / 26

14. Solving Nash
Solution 2: Approximate Nash Equilibrium
Approximate -NE
(x; y) such that
xTMy xTMy xTMy + :
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 9 / 26

15. Solution 1: LP (comp. expensive)
Solution 2: Approximate Nash Equilibrium
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 10 / 26

16. Solution 1: LP (comp. expensive)
Solution 2: Approximate Nash Equilibrium
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 10 / 26

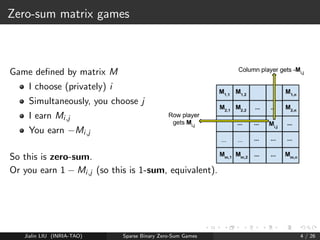
17. Computing approximate Nash Equilibrium
Assuming the matrix is of size K K ...
LP (see reduction from Nash to linear programming in
[Von Stengel (2002)]): O(K2) with 3 4
[Grigoriadis and Khachiyan(1995)]:
-Nash with expected time O(K log(K)
2 ), i.e. less than the size of the
matrix!
Parallel : O( log2(K)
2 ) if using K
log(K) processors
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 11 / 26

18. Computing approximate Nash Equilibrium
Assuming the matrix is of size K K ...
LP (see reduction from Nash to linear programming in
[Von Stengel (2002)]): O(K2) with 3 4
[Grigoriadis and Khachiyan(1995)]:
-Nash with expected time O(K log(K)
2 ), i.e. less than the size of the
matrix!
Parallel : O( log2(K)
2 ) if using K
log(K) processors
Other algorithms: similar complexity, approximate solution +

19. xed
time with probability 1
EXP3 ([Auer et al.(1995)])
Inf ([Audibert and Bubeck(2009)])
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 11 / 26

20. Other tools 1: Hadamard determinant
Hadamard determinant bound
([Hadamard(1893)], [Brenner and Cummings(1972)])
Given matrix Mkk with coecients in f1; 0; 1g, then M has
determinant at most k
k
2 , i.e.
j detMj k
k
2 :
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 12 / 26

21. Other tools 2: Linear programming
Solve
min ax
Mx c
x 2 Rd
If there is a

22. nite optimum, then there is a

23. nite optimum x such
that, for some E with jEj = d,
8i 2 E, Mi x = ci
the Mi for i in E are linear independent
(=) i.e. d lin. indep. constraints are active)
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 13 / 26

24. Why is this relevant ?
Nash = solution of linear programming problem
x: Nash Equilibrium of MKK
Let us assume that x is unique and has at most k non-zero
components (sparsity)
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 14 / 26

25. Why is this relevant ?
Nash = solution of linear programming problem
x: Nash Equilibrium of MKK
Let us assume that x is unique and has at most k non-zero
components (sparsity)
) x = also NE of a k k submatrix: Mk
) x = solution of LP in dimension k
) x = solution of k lin. eq. with coecients in f1; 0; 1g
) x = inv-matrix vector
) x = obtained by cofactors / det matrix
x k
) has denominator at most k
2
0k
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 14 / 26

26. How to realise ?
Under assumption that the Nash is sparse
x is rational with small denominator
So let us compute an -Nash (sublinear time!)
And let us compute its closest approximation with small
denominator (Hadamard)
variants for -Nash =) exact Nash
Rounding: switch to closest approximation
Truncation: remove small components and work on the remaining
submatrix (exact solving)
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 15 / 26

27. Evil in the details
jjy yjj1 does not imply V(y) V(y) + ;
indeed V(y) V(y) + jjyyjj1
k
k
2
Results : (if Grigoriadis)
For a K K matrix with Nash k-sparse
Exact solution in time O(poly (k) + (K log K)k3k ) with
truncation-algorithm
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 16 / 26

28. Experimental results: two card games
Previous results: ingaming of Urban Rivals
New results: metagaming of Pokemon
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 17 / 26

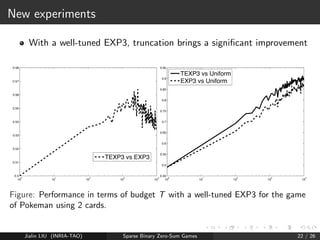
29. Ingaming results (Urban Rivals)
Previous work: [Flory and Teytaud(2011)], implementation of
Truncated-EXP3, without proof
Urban Rivals AI
= Monte Carlo Tree Search
([Coulom (2006)]),
using zero-sum matrix games
as a key component
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 18 / 26

30. Ingaming results (Urban Rivals)
Previous work: [Flory and Teytaud(2011)], implementation of
Truncated-EXP3, without proof
Results don't look impressive ( 56%), but the game is highly
randomized =) Reaching 55% is far from being negligible
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 19 / 26

31. New experiments
Test on Pokemon Deck choice (metagaming)
Based on EXP3+truncation
Various versions of EXP3 (6= parameters)
Code available https://www.lri.fr/~teytaud/games.html
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 20 / 26

32. New experiments
With a poorly tuned EXP3 : truncation brings a huge improvement
0
0.9
0.85
0.8
0.75
0.7
0.65
0.6
0.55
0.5
10
1
10
2
10
3
10
4
10
0.45
TEXP3 vs EXP3
0
0.9
0.85
0.8
0.75
0.7
0.65
0.6
0.55
0.5
10
1
10
2
10
3
10
4
10
0.45
TEXP3 vs Uniform
EXP3 vs Uniform
Figure: Performance in terms of budget T with a poorly tuned EXP3 for the
game of Pokeman using 2 cards.
Jialin LIU (INRIA-TAO) Sparse Binary Zero-Sum Games 21 / 26