Download as PDF, PPTX
MUMS Opening Workshop - Extrapolation: The Art of Connecting Model-Based Predictions to Reality - Dave Higdon, August 22, 2018
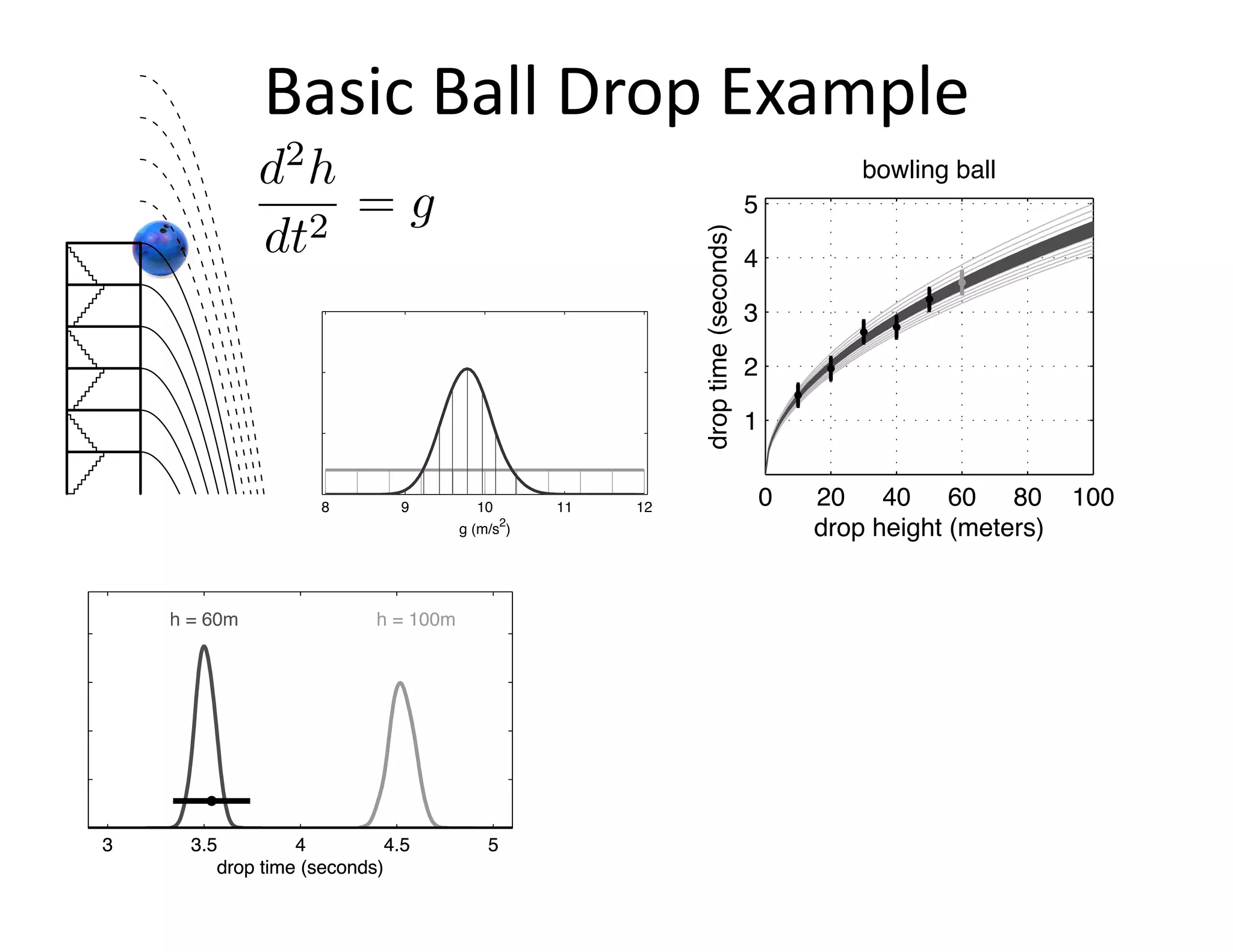
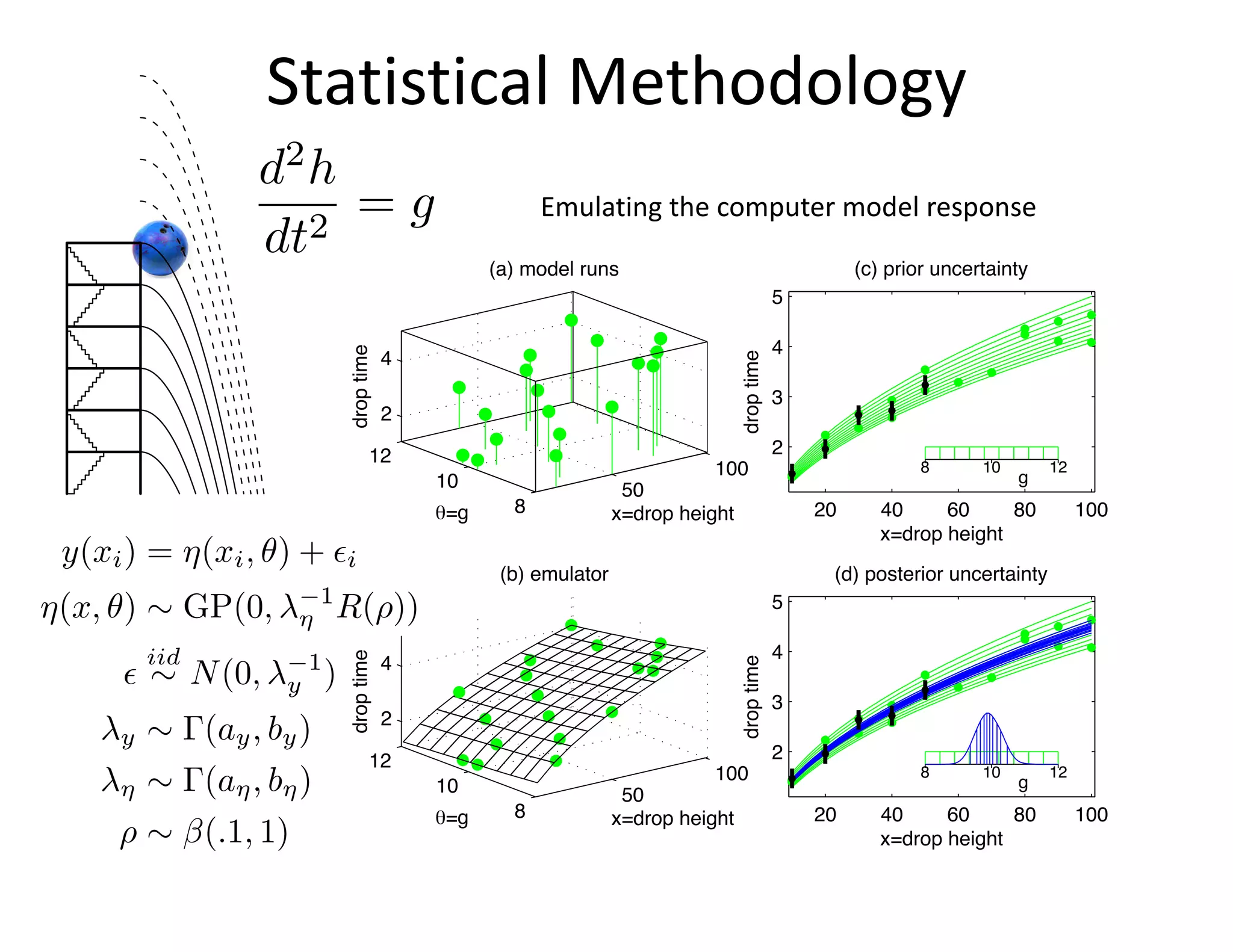
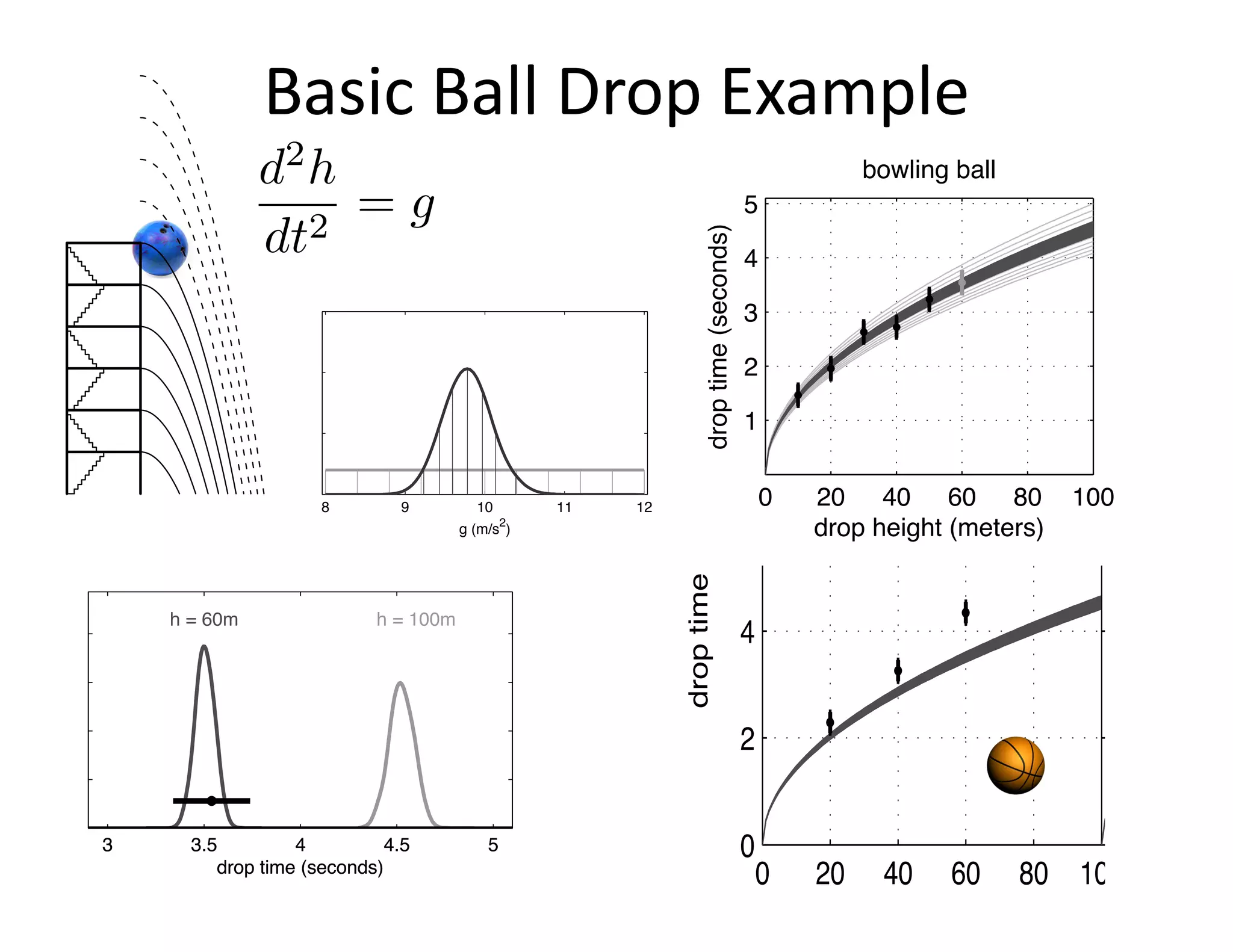
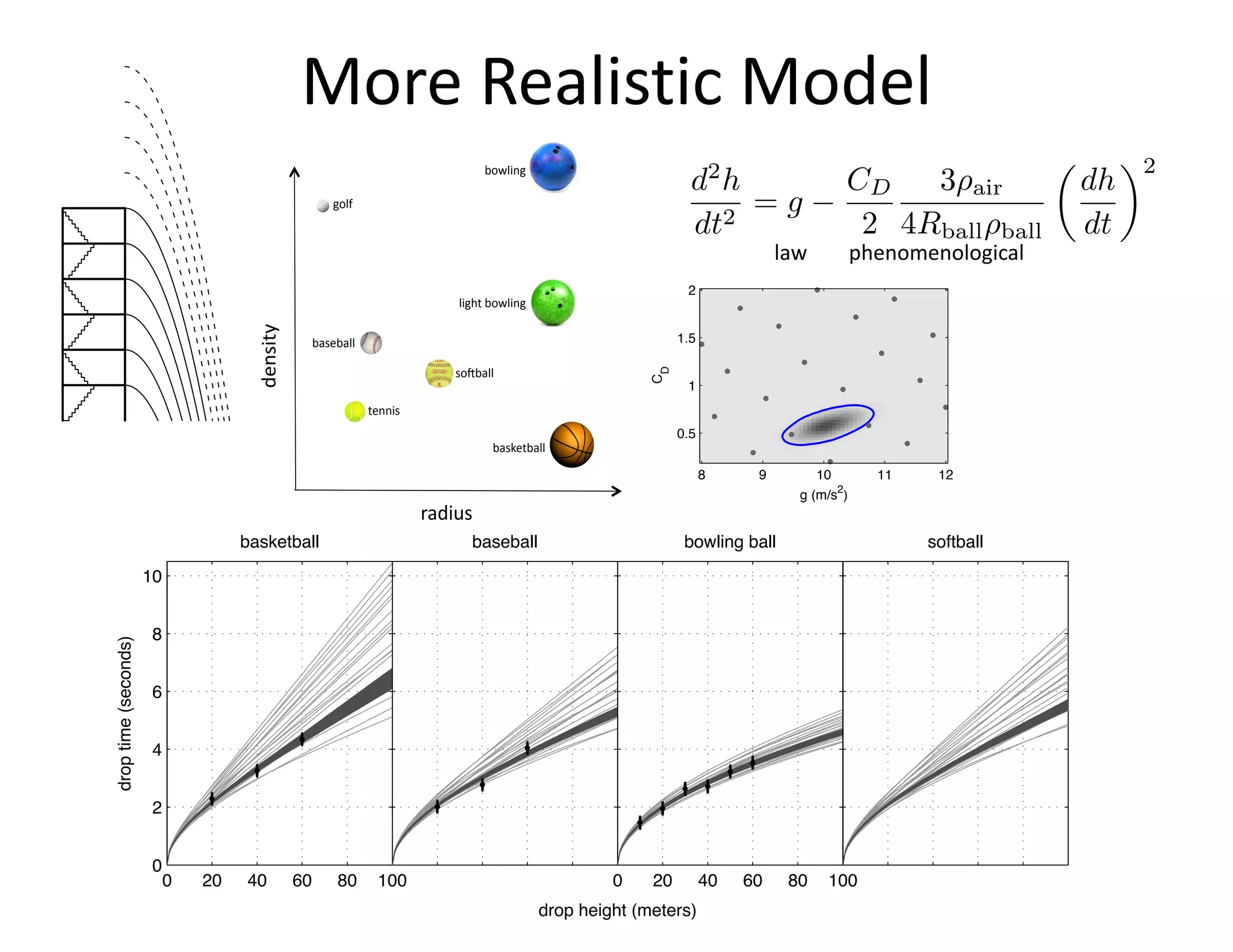
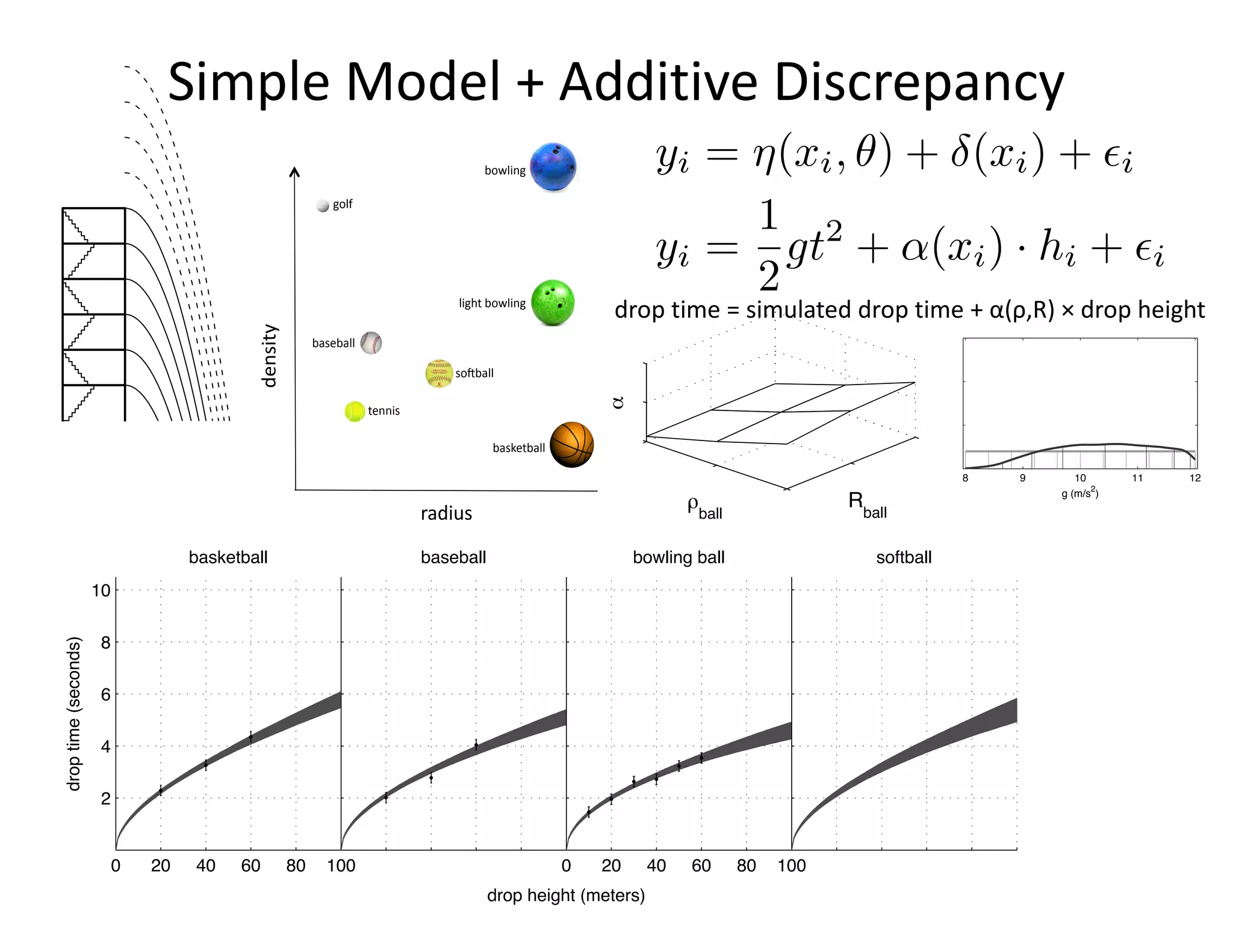
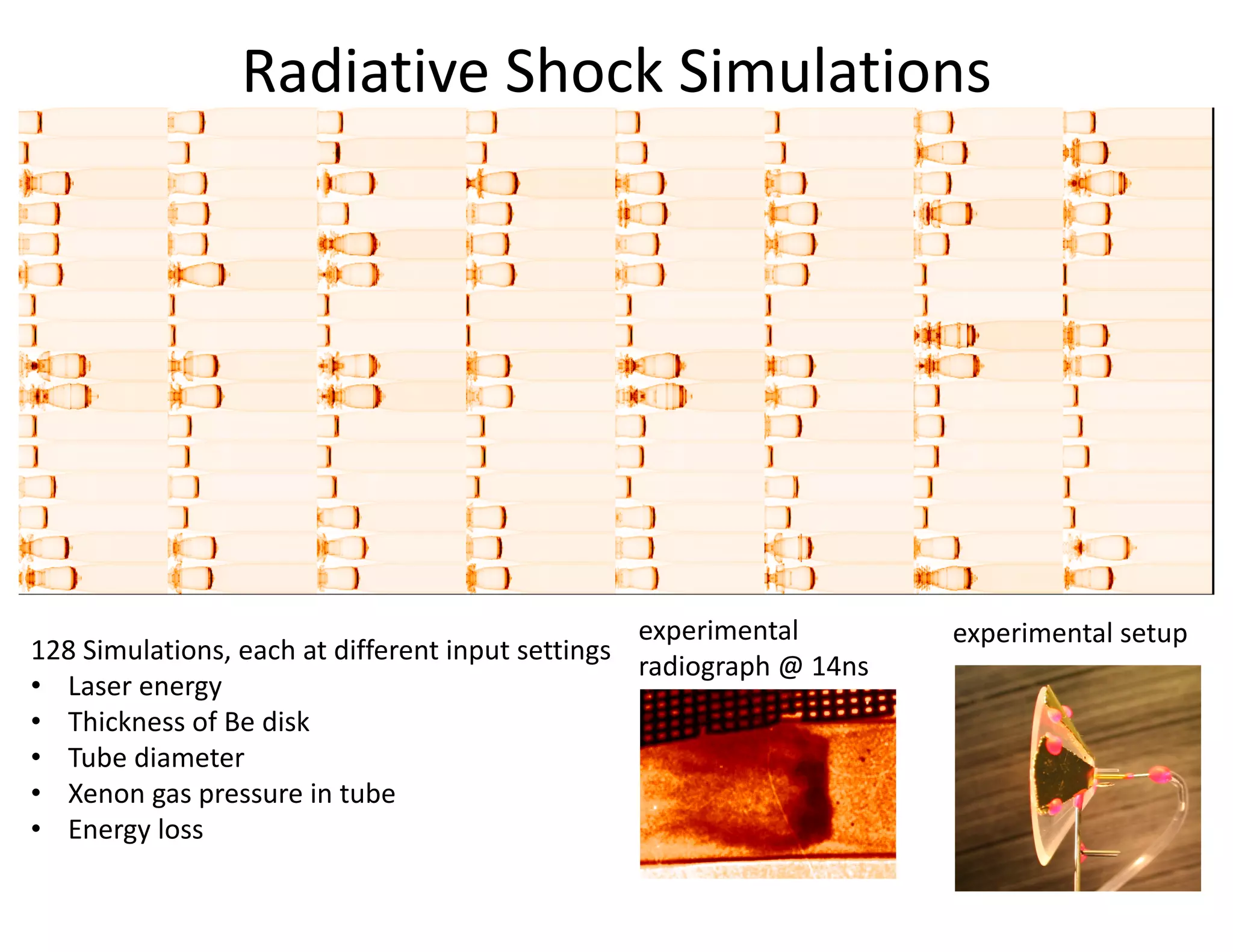
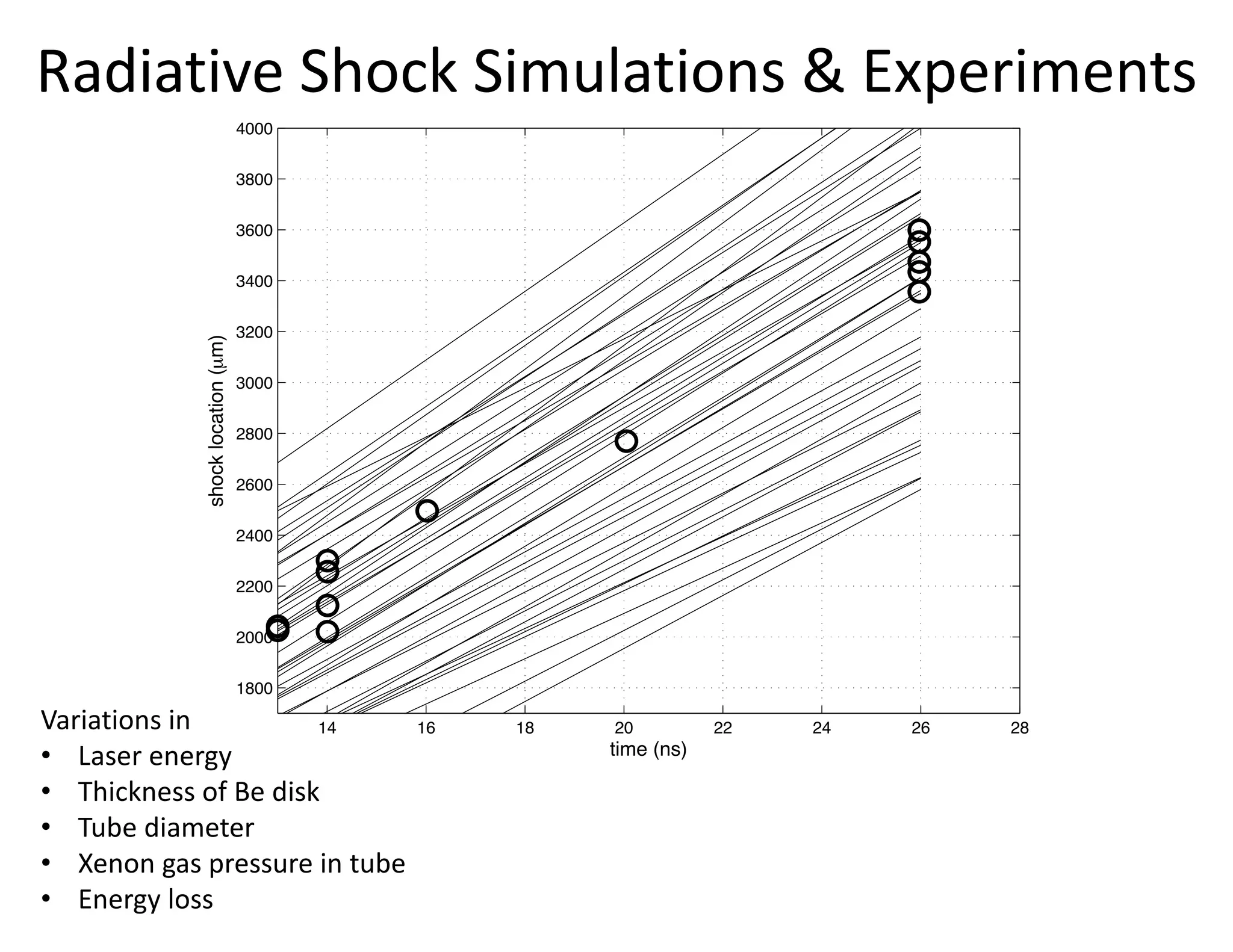
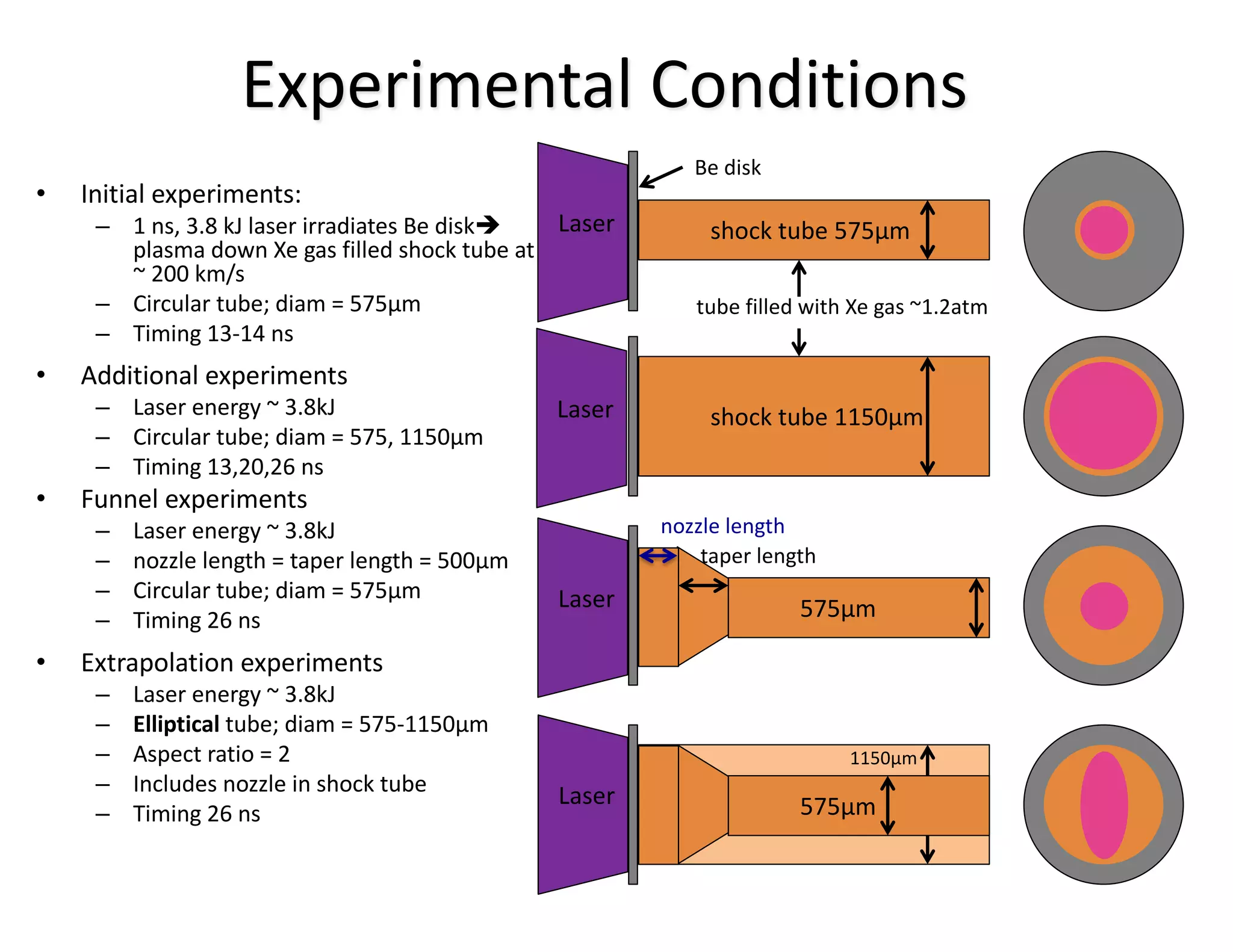
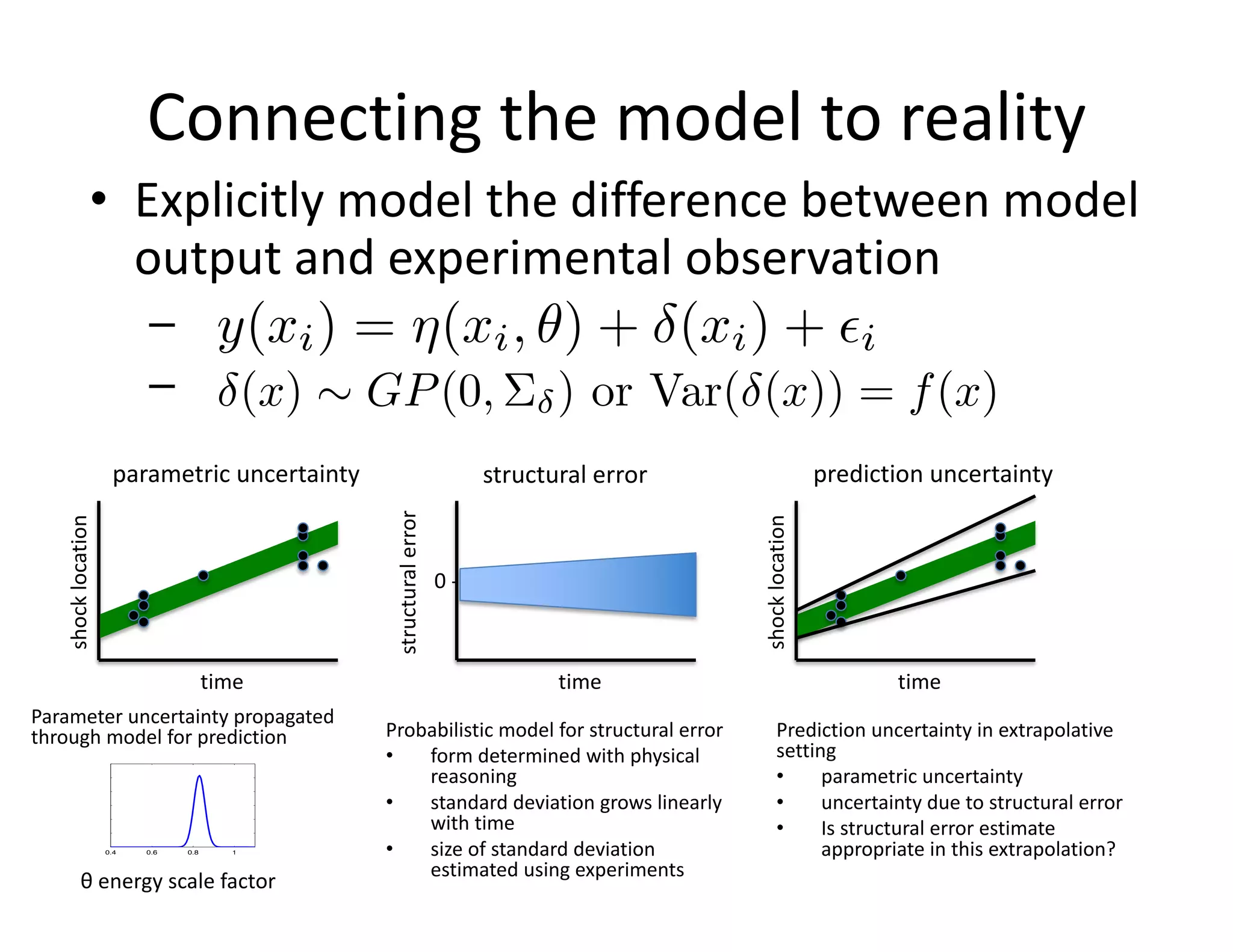
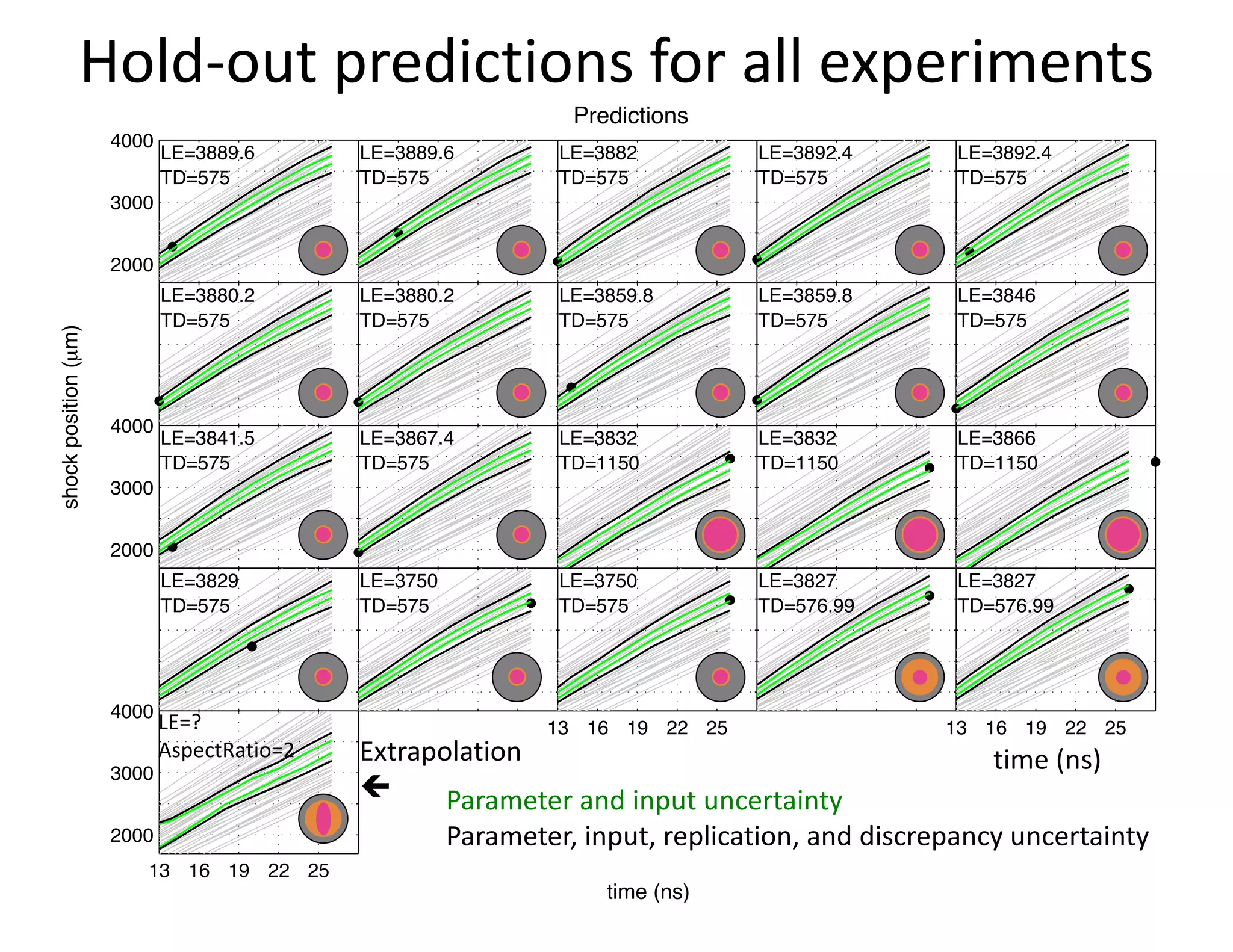
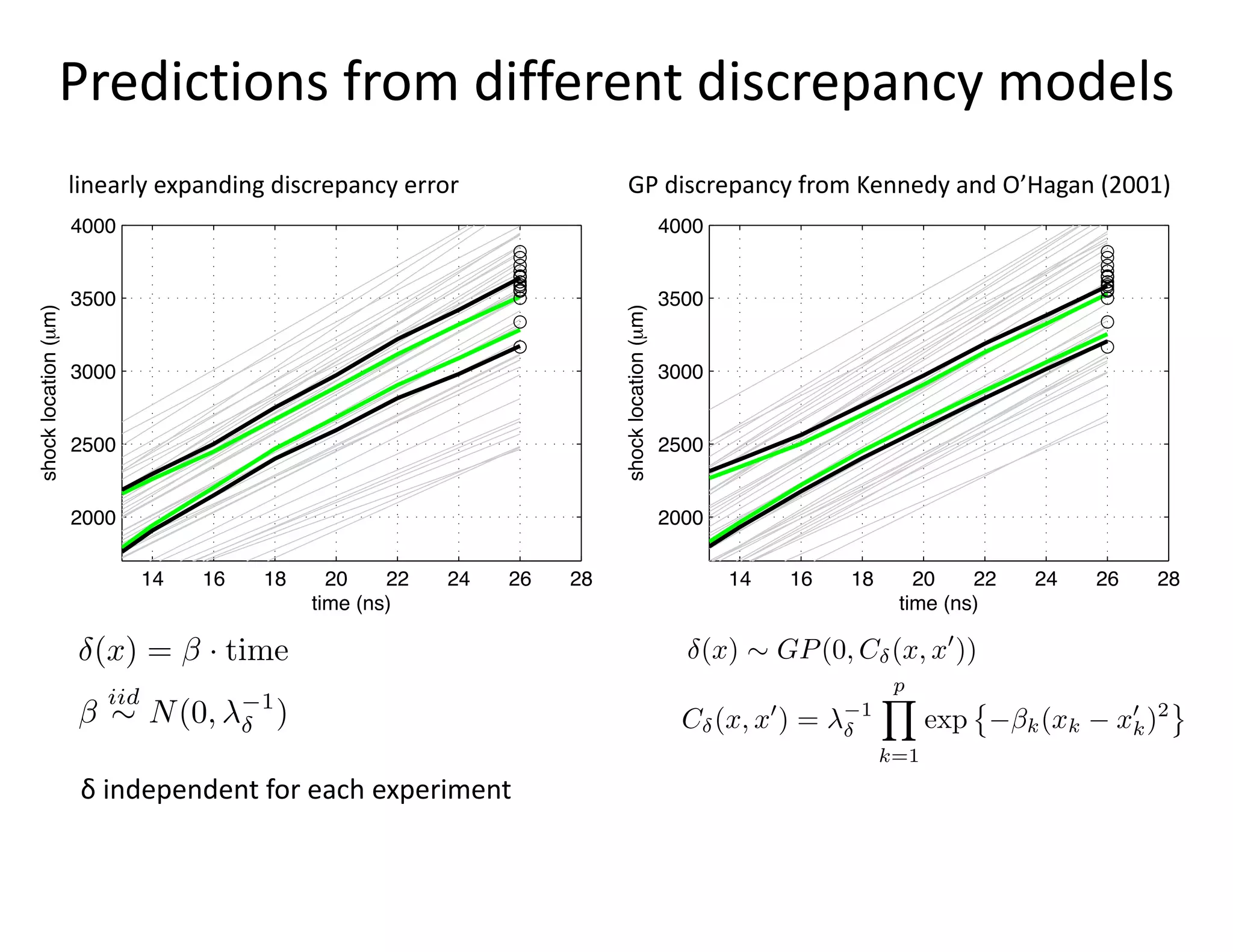
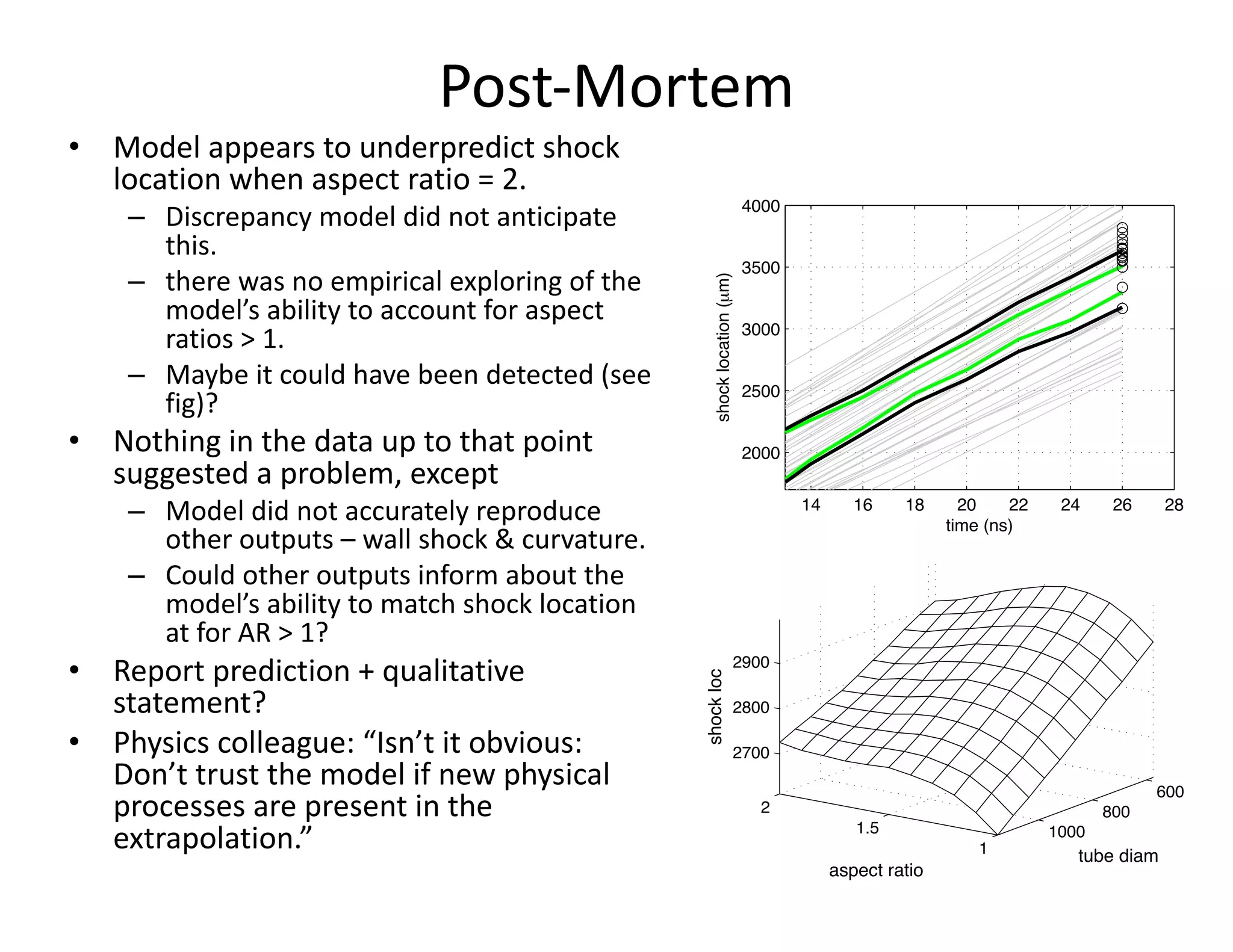
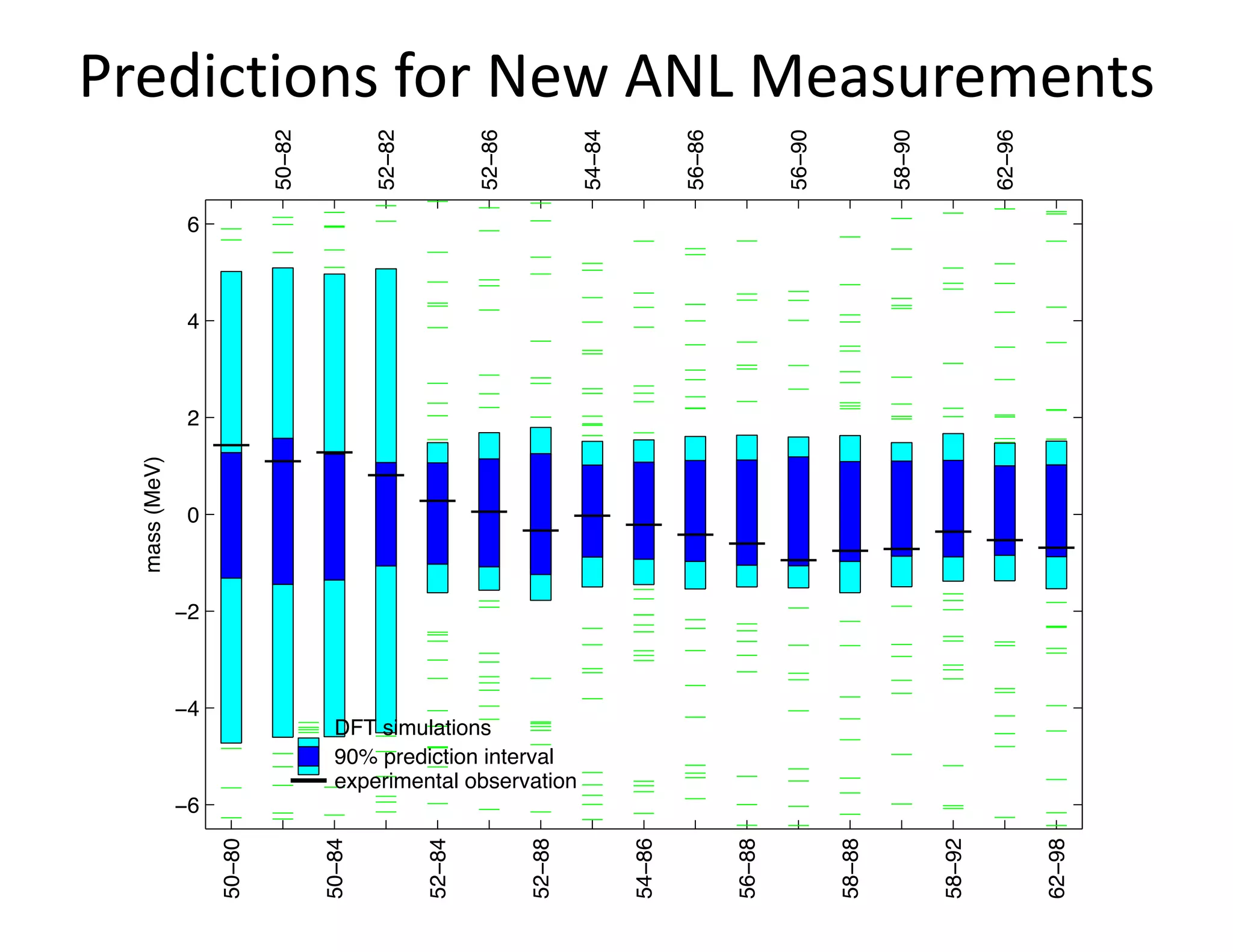
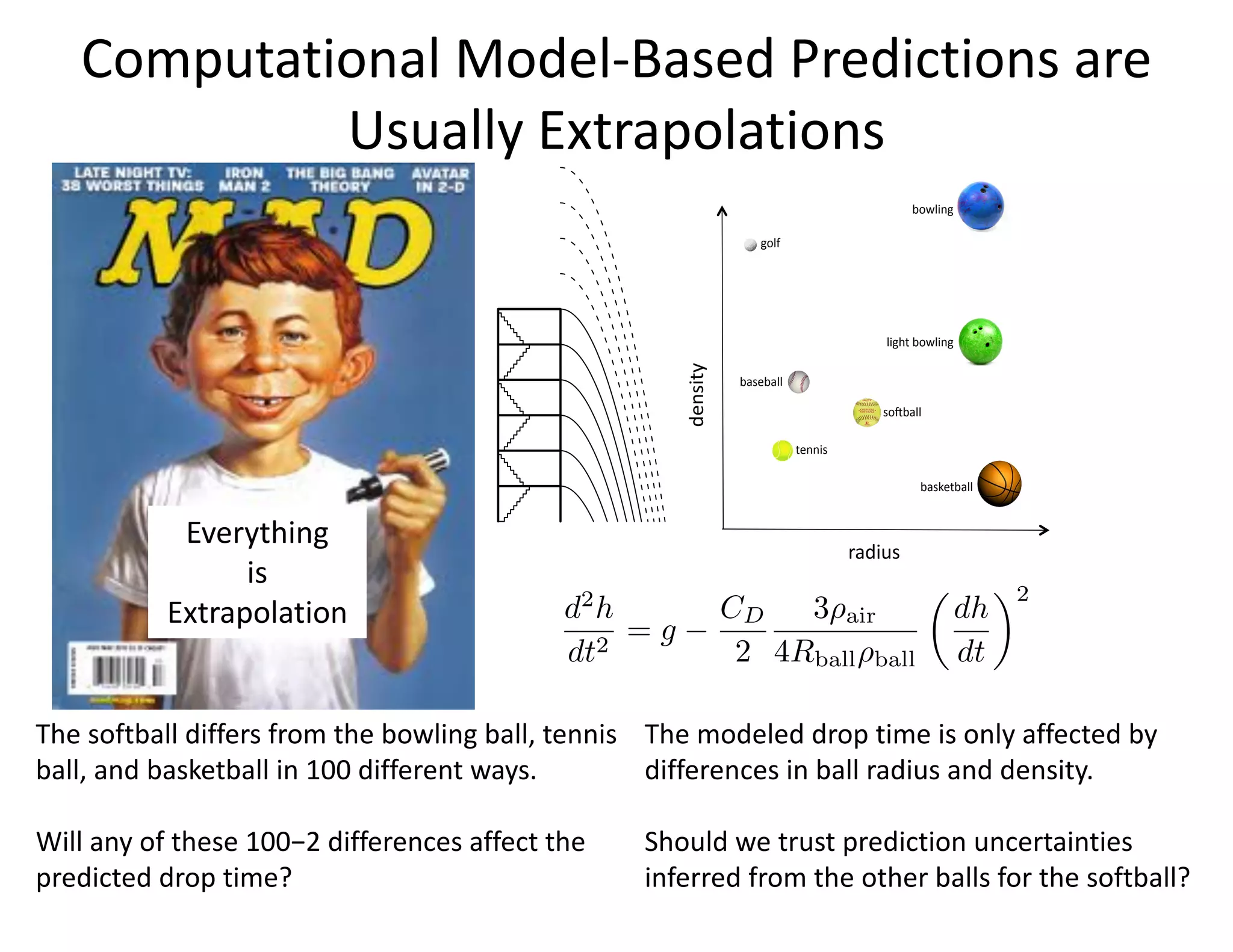
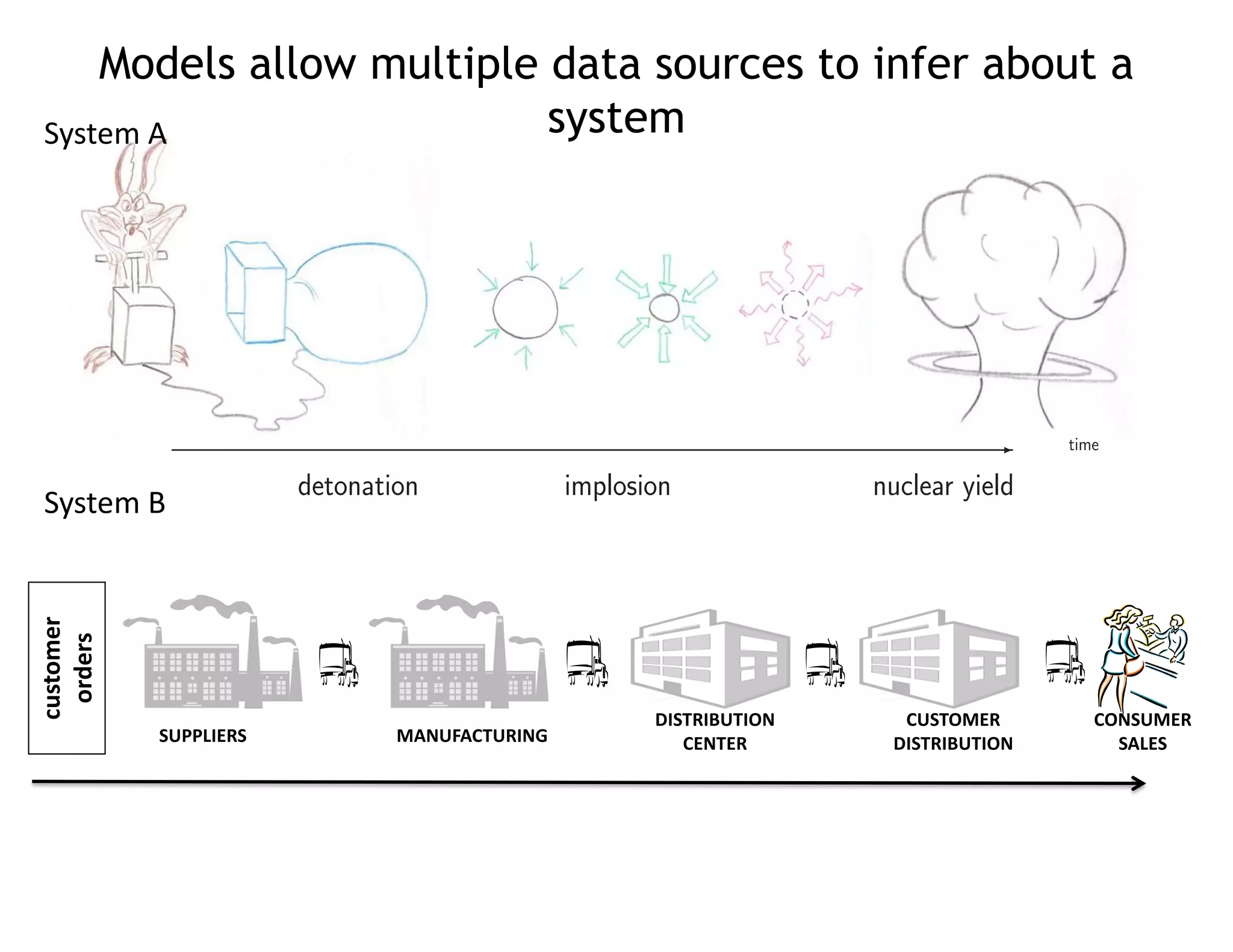
The document discusses methods for quantifying uncertainty in extrapolative predictions using statistical and computational models, focusing on experiments such as dropping balls from heights and radiative shock simulations. It highlights the importance of understanding model limitations and discrepancies when predicting outcomes in extrapolation scenarios. Several examples illustrate the application of these methodologies to improve predictions and manage uncertainties in various experimental settings.
More Related Content
Similar to MUMS Opening Workshop - Extrapolation: The Art of Connecting Model-Based Predictions to Reality - Dave Higdon, August 22, 2018
More from The Statistical and Applied Mathematical Sciences Institute
MUMS Opening Workshop - Extrapolation: The Art of Connecting Model-Based Predictions to Reality - Dave Higdon, August 22, 2018
- 1. Towards Quantifying Uncertaintyin Extrapolative Predictions Dave Higdon, Statistical Sciences, Los Alamos National Laboratory Derek Bingham, Statistics & Actuarial Science, Simon Fraser University Joslin Goh, Statistics & Actuarial Science, Simon Fraser University Mike Grosskopf, University of Michigan M Adams, TAMU, D. Higdon VT, J. Berger Duke, D. Bingham SFU, W. Chen, Northwestern, R. Ghanem, USC, O. Ghattas, UTexas, J. Meza, UCMerced; E. Michielssen, Mich, V. Nair, Mich, C. Nakhleh, LANL, D Nychka, NCAR, S. Pollock, Mich, H. Stone, Princeton, A. Wilson, NCSU, M. Zika, LLNL. Paul Drake, UMich; James Holloway, Mich; Ken Powell, CRASH; Quentin Stout, CRASH, Marvin Adams, TAMU, Joslin Goh, SFU; Mike Grosskopf, SFU; Erica Rutter, CRASH, Patrick Poon, CRASH; Bruce Fryxell, UMich; Natasha Andranoa, CRASH; Carolyn Kuranz, CRASH; Paul Keite, CRASH; Forrest Doss, CRASH; Gabor Toth, CRASH; Igor Sokolov, CRASH; Bart van der Holst, CRASH; Eric Myr, CRASH; Ben Torralva, CRASH; Bani Mallick, TAMU; Vijay Nair UMich; Lenny Smith, LSE; Todd Oliver, UT; Don Haynes, LANL; Mike Zika, LLNL; Leanna House, VaTech; Yousef Marzouk, MIT; Bob Moser, UT Jordan McDonnell, FrMarion; Nicolas Schunck, LLNL; Jason Sarich, ANL; Stefan Wild, ANL; Witek Nazarewicz, FRIB
- 2. M Adams, TAMU, D.Higdon VT, J. Berger Duke, D. Bingham SFU, W. Chen, Northwestern, R. Ghanem, USC, O. Ghattas, Utexas, J. Meza, UCMerced; E. Michielssen, Mich, V. Nair, Mich, C. Nakhleh, LANL, D Nychka, NCAR, S. Pollock, Mich (retired); H. Stone, Princeton, A. Wilson, NCSU, B. M. Zika, LLNL.
- 3. Basic Ball DropExample 8 9 10 11 12 g (m/s 2 ) 3 3.5 4 4.5 5 drop time (seconds) h = 60m 3 3.5 4 4.5 5 drop time (seconds) h = 60m h = 100m d2 h dt2 = g 0 20 40 60 80 100 1 2 3 4 5 bowling ball droptime(seconds) drop height (meters)
- 4. 50 100 8 10 12 2 4 x=drop height (a) modelruns =g droptime 20 40 60 80 100 2 3 4 5 x=drop height droptime g 8 10 12 (c) prior uncertainty 50 100 8 10 12 2 4 x=drop height (b) emulator =g droptime 20 40 60 80 100 2 3 4 5 x=drop height droptime g 8 10 12 (d) posterior uncertainty Statistical Methodology d2 h dt2 = g Emulating the computer model response y(xi) = ⇤(xi, ⌅) + ⇥i ⇤(x, ⌅) ⇠ GP(0, ⇧ 1 R(⌃)) ⇥ iid ⇠ N(0, ⇧ 1 y ) ⇧y ⇠ (ay, by) ⇧ ⇠ (a , b ) ⌃ ⇠ (.1, 1)
- 5. Basic Ball DropExample 8 9 10 11 12 g (m/s 2 ) 3 3.5 4 4.5 5 drop time (seconds) h = 60m 3 3.5 4 4.5 5 drop time (seconds) h = 60m h = 100m d2 h dt2 = g 0 20 40 60 80 100 1 2 3 4 5 bowling ball droptime(seconds) drop height (meters) 0 20 40 60 80 100 0 2 4 6 8 10 droptime(seconds) basketball b
- 6. More Realistic Model Simple'case'study:'dropping'balls'from' a'tower' • Can'get'field'data'from'tossing' objects'off'of'floors'1=6.' • Have'computaBonal'model' which'predicts'drop'Bmes' given'ball'radius,'density,'and' floor.' • ComputaBonal'model'has' parameter'for'air'fricBon'which' depends'on'cross'secBon,' density'and'velocity.' • Have'baseball,'basketball,'golf' ball,'tennis,'light'&'heavy' bowling'balls.' • Want'to'predict'soHball'drop' Bme'from'10th'floor'(100m).' • Also'want'to'understand'the' value'of'various'types'of' potenBal'experiments'&' simulaBons'for'the'soHball' predicBon'at'100m.' Slide'1' radius' density' physics'design'space' golf' baseball' tennis' soHball' basketball' light'bowling' bowling' d2 h dt2 = g CD 2 3 air 4Rball ball ✓ dh dt ◆2 CD g (m/s 2 ) 8 9 10 11 12 0.5 1 1.5 2 0 20 40 60 80 100 0 2 4 6 8 10 droptime(seconds) basketball baseball 0 20 40 60 80 100 bowling ball softball drop height (meters) law phenomenological
- 7. Simple Model +Additive Discrepancy Simple'case'study:'dropping'balls'from' a'tower' • Can'get'field'data'from'tossing' objects'off'of'floors'1=6.' • Have'computaBonal'model' which'predicts'drop'Bmes' given'ball'radius,'density,'and' floor.' • ComputaBonal'model'has' parameter'for'air'fricBon'which' depends'on'cross'secBon,' density'and'velocity.' • Have'baseball,'basketball,'golf' ball,'tennis,'light'&'heavy' bowling'balls.' • Want'to'predict'soHball'drop' Bme'from'10th'floor'(100m).' • Also'want'to'understand'the' value'of'various'types'of' potenBal'experiments'&' simulaBons'for'the'soHball' predicBon'at'100m.' Slide'1' radius' density' physics'design'space' golf' baseball' tennis' soHball' basketball' light'bowling' bowling' 0 20 40 60 80 100 2 4 6 8 10 droptime(seconds) basketball baseball 0 20 40 60 80 100 bowling ball softball drop height (meters) Rballball drop time = simulated drop time + α(ρ,R) × drop height 8 9 10 11 12 g (m/s 2 ) yi = ⌘(xi, ✓) + (xi) + ✏i yi = 1 2 gt2 + ↵(xi) · hi + ✏i
- 8. Connecting the modelto reality • Assume model = reality (at appropriate θ) – – absorb model inadequacy into measurement error • Parameterize missing processes within the computational model – e.g. • Explicitly model the difference between model and reality – – y(xi) = ⇥(xi, ⇤) + i d2 h dt2 = g CD 2 3 air 4Rball ball ✓ dh dt ◆2 y(xi) = ⇤(xi, ⌅) + (xi) + ⇥i (x) ⇠ GP(0, ) or Var( (x)) = f(x)
- 9. Three Extrapolation Examples •Radiative Shocks • Binding Energies • Ball Dropping CRASH Center University of Michigan NUCLEI Collaboration National Labs + Universities DOE NNSA activity to better deal with extrapolations
- 10. Radiative Shock Simulations 128Simulations, each at different input settings • Laser energy • Thickness of Be disk • Tube diameter • Xenon gas pressure in tube • Energy loss experimental radiograph @ 14ns experimental setup
- 11. 14 16 1820 22 24 26 28 1800 2000 2200 2400 2600 2800 3000 3200 3400 3600 3800 4000 shocklocation(µm) time (ns) Radiative Shock Simulations & Experiments Variations in • Laser energy • Thickness of Be disk • Tube diameter • Xenon gas pressure in tube • Energy loss
- 12. shock tube 1150μmLaser shocktube 1150μm575μm 1150μm Laser shock tube 575μmLaser Be disk 575μmLaser taper length nozzle length • Initial experiments: – 1 ns, 3.8 kJ laser irradiates Be diskè plasma down Xe gas filled shock tube at ~ 200 km/s – Circular tube; diam = 575μm – Timing 13-14 ns • Additional experiments – Laser energy ~ 3.8kJ – Circular tube; diam = 575, 1150μm – Timing 13,20,26 ns • Funnel experiments – Laser energy ~ 3.8kJ – nozzle length = taper length = 500μm – Circular tube; diam = 575μm – Timing 26 ns • Extrapolation experiments – Laser energy ~ 3.8kJ – Elliptical tube; diam = 575-1150μm – Aspect ratio = 2 – Includes nozzle in shock tube – Timing 26 ns tube filled with Xe gas ~1.2atm Experimental Conditions
- 13. Connecting the modelto reality • Explicitly model the difference between model output and experimental observation – – y(xi) = ⇤(xi, ⌅) + (xi) + ⇥i (x) ⇠ GP(0, ) or Var( (x)) = f(x) 0.4 0.6 0.8 1 − energy scale factor θ energy scale factor time shocklocation time structuralerror 0 - time shocklocation parametric uncertainty structural error prediction uncertainty Probabilistic model for structural error • form determined with physical reasoning • standard deviation grows linearly with time • size of standard deviation estimated using experiments Parameter uncertainty propagated through model for prediction Prediction uncertainty in extrapolative setting • parametric uncertainty • uncertainty due to structural error • Is structural error estimate appropriate in this extrapolation?
- 14. 2000 3000 4000 LE=3889.6 TD=575 LE=3889.6 TD=575 LE=3882 TD=575 LE=3892.4 TD=575 LE=3892.4 TD=575 LE=3880.2 TD=575 LE=3880.2 TD=575 LE=3859.8 TD=575 LE=3859.8 TD=575 LE=3846 TD=575 2000 3000 4000 LE=3841.5 TD=575 LE=3867.4 TD=575 LE=3832 TD=1150 LE=3832 TD=1150 LE=3866 TD=1150 LE=3829 TD=575 LE=3750 TD=575 13 16 1922 25 LE=3750 TD=575 LE=3827 TD=576.99 13 16 19 22 25 LE=3827 TD=576.99 13 16 19 22 25 2000 3000 4000 Predictions shockposition(µm) time (ns) Hold-out predictions for all experiments Parameter and input uncertainty Parameter, input, replication, and discrepancy uncertainty Extrapolation ç LE=? AspectRatio=2 time (ns)
- 15. Predictions from differentdiscrepancy models 14 16 18 20 22 24 26 28 2000 2500 3000 3500 4000 shocklocation(µm) time (ns) 14 16 18 20 22 24 26 28 2000 2500 3000 3500 4000 shocklocation(µm) time (ns) linearly expanding discrepancy error GP discrepancy from Kennedy and O’Hagan (2001) (x) ⇠ GP(0, C (x, x0 )) C (x, x0 ) = 1 pY k=1 exp k(xk x0 k)2 (x) = · time iid ⇠ N(0, 1 ) δ independent for each experiment
- 16. 14 16 1820 22 24 26 28 2000 2500 3000 3500 4000 shocklocation(µm) time (ns) Post-Mortem • Model appears to underpredict shock location when aspect ratio = 2. – Discrepancy model did not anticipate this. – there was no empirical exploring of the model’s ability to account for aspect ratios > 1. – Maybe it could have been detected (see fig)? • Nothing in the data up to that point suggested a problem, except – Model did not accurately reproduce other outputs – wall shock & curvature. – Could other outputs inform about the model’s ability to match shock location at for AR > 1? • Report prediction + qualitative statement? • Physics colleague: “Isn’t it obvious: Don’t trust the model if new physical processes are present in the extrapolation.” 1 1.5 2 600 800 1000 2700 2800 2900 tube diam aspect ratio shockloc
- 17. Binding Energy ofNuclei • Often called “mass” • Measured experimentally • Calculated using various computational models. – DFT for large nuclei BE(N,Z) per nucleon as predicted from a simple empirical model Curve of Binding Energy neutrons N atomicnumberZ N+Z
- 18. Nuclear Density FunctionalTheory (DFT) • Built on an effective field approximating nuclear forces between nucleons • Uses densities of nucleons as main building blocks DFT solver determines ρ, τ, J for specified parameters E = Z " Ekin(r) + ECou(r) + Epair(r) + X t=0,1 t(r) # d3 r ⇤t(r) =C⇥⇥ t 2 t + C⇥⇤ t t⇥t + CJJ t X µ Jµ ,tJµ ,t + C⇥ ⇥ t t t + C⇥rJ t t · Jt
- 19. Predicting Masses forPreviously Unobserved NucleiAtomicnumber Number of neutrons neutron-rich nuclei stable super-heavy nuclei? extrapolative DFT- based predictions Pb Sn Ni Ca O
- 20. Data & Statisticalmodel • yij denotes an experimental measurement – i denotes measurement type – sym-mass, def-mass, radius, fission isomer energy, odd-even staggering for neutrons, odd-even staggering for protons – j denotes nucleus (within a measurement type) – variance of errors depends on measurement type • θ denotes parameter 12-vector – want 12-d distribution to describe uncertainty – a priori, assume uniform over design rectangle • η(θ,i,j) denotes DFT result for measurement type i and nucleus j, at parameter setting θ. • Carry out 200 simulations at θ1,…,θ200 and estimate η(θ,i,j), for any θ, using a response surface (emulator). – inaccuracy in the emulator leads to additional uncertainty regarding θ. – also ran at UNDEF1 settings yij = ⌘(✓, i, j) + ij + ✏ij misfit experimental error
- 21. simulations experiment −1800 −1600 −1400 −1200 −1000 −800 −600 −400 −200 symmass(Mev) 20−20 20−24 20−28 28−28 28−32 28−36 50−62 50−66 50−70 50−74 82−118 82−122 82−126 82−130 20−22 20−26 20−30 28−30 28−34 50−58 50−64 50−68 50−72 82−116 82−120 82−124 82−128 82−132 −2100 −2000 −1900 −1800 −1700 −1600 −1500 −1400 −1300 −1200 −1100 defmass(Mev) 64−88 64−92 64−96 66−90 66−94 66−98 66−102 68−104 70−108 90−142 92−144 94−144 96−144 96−148 98−144 98−148 98−152 98−156 100−148 100−152 100−156 102−152 104−152 108−156 64−90 64−94 64−98 66−92 66−96 66−100 68−102 70−100 72−104 92−142 92−146 94−146 96−146 96−150 98−146 98−150 98−154 100−146 100−150 100−154 102−150 102−154 106−154 3 3.5 4 4.5 5 5.5 6 radii 20−20 20−24 20−28 28−28 28−32 28−36 50−62 50−66 50−70 50−74 82−118 82−122 82−126 82−130 20−22 20−26 20−30 28−30 28−34 50−58 50−64 50−68 50−72 82−116 82−120 82−124 82−128 82−132 −8 −6 −4 −2 0 2 4 6 8 10 fissionisomerenergies 92−144 94−146 92−146 96−146 0 0.5 1 1.5 2 2.5 3 OESneutrons 66−98 92−144 72−104 100−152 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 OESprotons 66−94 92−142 68−102 96−148 −1400 −1350 −1300 −1250 −1200 −1150 −1100 measuredmass(MeV) DFT simulations 90%prediction interval experimental observation 50−80 50−84 52−82 52−86 54−84 56−86 56−90 56−94 58−90 58−94 60−94 60−98 62−98 62−102 64−104 66−104 50−82 50−86 52−84 52−88 54−86 56−88 56−92 58−88 58−92 58−96 60−96 62−96 62−100 64−100 66−102 200 DFT simulations over the 12-d parameter space z: protons (atomic number) n: neutrons ANL mass measurements Ca Ni Sn Pb
- 22.
- 23.
- 24. Posterior uncertainty forθ −16 −15.5 28 30 0.8 1 1.2 −200−100 −220 −180 −80 0 −16 −15.5 200 220 240 28 30 20 40 60 0.8 1 1.2 −60 −40 −200 −100 −200 −150 −220 −200 −180 −80 −60 0.155 0.165 200 240 20 40 60 −60 −40 −200 −150 −80 −60 rc E NM /A K NM a NM sym L NM sym 1/M s * C rDr 0 CrDr 1 V n 0 Vp 0 CrÑJ 0 CrÑJ 1 UNEDF1Ÿ
- 25. Predictions for NewANL Measurements −1400 −1350 −1300 −1250 −1200 −1150 −1100 measuredmass(MeV) DFT simulations 90% prediction interval experimental observation 50−80 50−84 52−84 52−88 54−86 56−88 58−88 58−92 62−98 50−82 52−82 52−86 54−84 56−86 56−90 58−90 62−96 yij = ⌘(✓, i, j) + ij + ✏ij
- 26. Predictions for NewANL Measurements −6 −4 −2 0 2 4 6 mass(MeV) DFT simulations 90% prediction interval experimental observation 50−80 50−84 52−84 52−88 54−86 56−88 58−88 58−92 62−98 50−82 52−82 52−86 54−84 56−86 56−90 58−90 62−96
- 27. Predictions for NewANL Measurements −6 −4 −2 0 2 4 6 mass(MeV) DFT simulations 90% prediction interval experimental observation 50−80 50−84 52−84 52−88 54−86 56−88 58−88 58−92 62−98 50−82 52−82 52−86 54−84 56−86 56−90 58−90 62−96
- 28. Computational Model-Based Predictionsare Usually Extrapolations Everything is Extrapolation Simple'case'study:'dropping'balls'from a'tower' • Can'get'field'data'fro objects'off'of'floors'1 • Have'computaBonal'm which'predicts'drop'B given'ball'radius,'den floor.' • ComputaBonal'mode parameter'for'air'fric depends'on'cross'sec density'and'velocity.' • Have'baseball,'basket ball,'tennis,'light'&'he bowling'balls.' • Want'to'predict'soHb Bme'from'10th'floor'( • Also'want'to'understa value'of'various'types potenBal'experiment simulaBons'for'the'so predicBon'at'100m.' Slide'1' radius' density' physics'design'space' golf' baseball' tennis' soHball' basketball' light'bowling' bowling' The softball differs from the bowling ball, tennis ball, and basketball in 100 different ways. Will any of these 100−2 differences affect the predicted drop time? d2 h dt2 = g CD 2 3 air 4Rball ball ✓ dh dt ◆2 The modeled drop time is only affected by differences in ball radius and density. Should we trust prediction uncertainties inferred from the other balls for the softball?
- 29. Regression & Extrapolation:y = f(x) • Mathematically, all large p problems are extrapolations! • But, regression + model selection + assumptions of smoothness (regularity) often result in accurate predictions for large p – small n problems. – Gaussian Process – LASSO – Compressive Sensing – Random Forests, BART,… • Common practice: split data into “training” x and “test” x* sets • Freedom in how f(x) is chosen • Works when effect sparsity is present • Data split à not extrapolation! y = xf( ) + ε y = x*f( )y* ⌃compare
- 30. Models allow multipledata sources to infer about a systemCombining information and quality of models ✲ time detonation implosion nuclear yield ✇ ✇ implosion experiments ✇ ✇ sub-critcal experiments ✇ ✇ historical nuclear tests ✇ ✇ ✇ off-line experiments materials, equations of state (EOS), high explosive (HE) System A System B SUPPLIERS MANUFACTURING CUSTOMER DISTRIBUTION DISTRIBUTION CENTER CONSUMER SALES customer orders
- 31.
- 37. Ending thoughts onprediction & extrapolation • “Prediction is hard, especially about the future.” – Niels Bohr • Very often (always?) we’d like to make extrapolations – How can statistics/math/UQ help? • Understanding of “domain space” – Need to understand what predictions are/are not extrapolations – Determine conditions for which model predictions can be trusted – Construct error model (discrepancy) over this domain space. • Decompose model into trusted & phenomenological components – e.g. F=ma and drag (Moser, Terejanu, Oliver, Simmons 2012). – add thoughtful stochastic terms to the phenomenological components • Multiple model approaches – Success in data assimilation – can it be adapted to UQ applications? – Can one build ensembles where one could relate the ensemble to reality? • Highly parameterized models that cover reality • Theoretical approaches (e.g. bounding tail probabilities, bounding model errors) – Useful worst-case analyses?