Tensor Eigenvectors and Stochastic Processes

Tensor eigenvectors and
stochastic processes
Austin R. Benson · Cornell
David F. Gleich · Purdue
Act 1. 10:45-10:55am Overview
Act 2. 10:55-11:05am Motivating applications
Act 3. 11:05-11:30am Stochastic processes & Markov
chains
Act 4. 11:40-12:10pm Spacey random walk stochastic
process
Act 5. 12:10-12:30pm Theory of spacey random walks SIAM ALA'18Benson & Gleich 1
Papers, slides, & code ⟶ bit.ly/tesp-web, bit.ly/tesp-code
A
3
2
1

Stochastic processes offer a new and exciting set
of opportunities and challenges in tensor
algorithms.
After this is done, you should know a little bit about
And where to look for more info! bit.ly/tesp-web
1
3
2
P
• Tensor eigenvectors
• Z-eigenvectors
• Irreducible tensors
• Higher-order Markov chains
• Spacey random walks
• Vertex reinforced random walks
• Dynamical systems for trajectories
• Fitting spacey random walks to data
• Multilinear PageRank models
• Clustering tensors
• And lots of open problems in this area!
SIAM ALA'18Benson & Gleich 2

A quick overview of where we are going to go in
this tutorial and some rough timing.
Act 1. This overview
• Basic notation and operations
• The fundamental problems
Act 2. Motivating applications
• Compression
• Diffusion imaging
• Hardy-Weinberg genetics
Act 3. Review of Stochastic processes
Markov Chains & Higher-order chains
• Limiting and stationary distributions
• Irreducibility
Act 4. Spacey RWs as stochastic processes
• Pause for interpretations and thought
• FAQ
Act 5. Theory of spacey random walks
• Limiting dists are tensor evecs
• Dynamical systems & vertex reinforced
• (Non-) existence, uniqueness,
• Computation
Act 6. Applications of spacey random
walks
• Pólya urns, sequence data, tensor
• New algorithm for computing tensor

A note.
We tried to be a friendly tutorial instead of
trying to be comprehensive!
See the extensive work by HK groups!

3
2
1
Fundamental notations and some helpful pictures
tensor-vector product tensor-collapse product

Summary of fundamental notations
We assume the tensor is symmetric or permuted so the last operations are all that’s needed.

The tensor Z-eigenvector problem has different
properties than matrix eigenvectors

There are many generalizations of eigen-problems
to tensors. Their properties are very different.
All eigenvectors have unit 2-norm. ||x||2 = 1.
The H-eigenvalue spectrum is scale invariant.

There are many generalizations of eigen-problems
to tensors. Their properties are very different.
All eigenvectors have unit 2-norm. ||x||2 = 1.
Z-eigenvectors are not scale invariant. H-eigenvectors are.
There are even more types of eigen-probs!
• D-eigenvalues
• E-eigenvalues (complex Z-eigenvalues)
• Generalized versions too…
• Other normalizations! [Lim 05]
For more information about these tensor
eigenvectors and some of their fundamental
properties, we recommend the following resources
• Tensor Analysis: Spectral Theory and Special
Tensors. Qi & Luo, 2017.
• A survey on the spectral theory of nonnegative
tensors. Chang, Qi, & Zhang, 2013.

algorithms.
Usually, the properties of these objects are explored algebraically or through
polynomial interpretations.
Our tutorial focuses on interpreting the tensor objects stochastically!
A
3
2
1

• Compression
• Irreducibility
Act 4. Spacey RWs as stochastic
processes
• Pause for interpretations and
• FAQ
• Dynamical systems & vertex
RWs
• Computation
walks
clustering

The best rank-1 approximation to a symmetric
tensor is given by the principal eigenvector.
[De Lathauwer 97; De Lathauwer-De Moor-Vandewalle 00; Kofidis-Regalia 01, 02]
A is a symmetric if the entries are the same under any
permutation of the indices.
In data mining and signal processing applications, we
are often interested in the “best” rank-1 approximation.
Notes. The first k tensor eigenvectors do not necessarily give the best rank-
k approximation. In general, this problem is not even well-posed [de Silva-
Lim 08].
Furthermore, the first eigenvector is not necessarily in the best rank-k
“orthogonal approximation” from orthogonal vectors [Kolda 01, 03].
3
2
1

Quantum
entanglement
A(i,j,k,…,l) are the normalized
amplitudes of an m-partite pure
state |ψ>
A is a nonneg sym tensor
Diffusion imaging
W is a symmetric, fourth-order kurtosis
diffusion tensor
D is a symmetric, 3 x 3 matrix
⟶ both are measured from MRI data.
Michael S. Helfenbein
Yale University
https://www.eurekalert.org/pub_r
eleases/2016-05/yu-
ddo052616.php
[Wei-Goldbart 03; Hu-Qi-Zhang
16]
is the geometric
measure of
entanglement
Paydar et al., Am. J. of
Neuroradiology, 2014
[Qi-Wang-Wu 08]

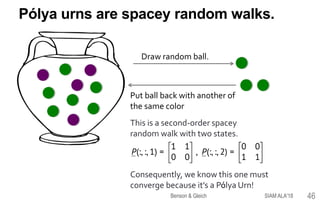
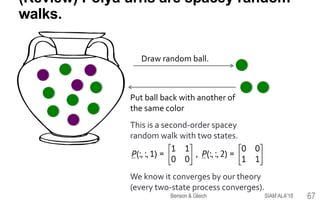
Markovian binary
trees.
Entry-wise minimal solutions
to x = Bx2 + a are extinction
Distribution of alleles (forms of a gene)
in a population at time t is x.
Start with an infinite population.
1. Every individual gets a random
mate.
2. Mates of type j and k produce
offspring of type i with probability
P(i, j, k) and then die.
Hardy-Weinberg equilibria of random mating
models are tensor eigenvectors.
Under Hardy-
Weinberg
equilibria
(steady-state), x
satisfies x = Px2.
[Bean-Kontoleon-Taylor 08;
Bini-Meini-Poloni 11; Meini-Poloni 11, 17]

• Compression
Act 3. Review of Stochastic
Markov Chains & Higher-order
• Limiting and stationary
• Irreducibility
processes
• FAQ
RWs
• Computation
walks
clustering

Markov chains, matrices, and eigenvectors have a
long-standing relationship.
[Kemeny-Snell 76] “In the land of Oz they never have two nice
days in a row. If they have a nice day, they are just as likely to
have snow as rain the next day. If they have snow or rain, they
have an even chance of having the same the next day. If there
is a change from snow or rain, only half of the time is this
change to a nice day.”
Column-stochastic in this tutorial
(since we are linear algebra people).
Equations for stationary distribution x.
The vector x is an
eigenvector of P.
Px = x.

Markov chains are a special case of a stochastic
process.
Stochastic processes are a (possibly infinite) sequence of RV.
Z1, Z2, …, Zt, Zt+1, …
• Zt is a random variable.
• This is a discrete time stochastic process
Stochastic processes are models throughout applied math and life
• The weather
• The stock market
• Natural language
• Random walks on graphs
• Pólya’s urn
• Brownian motion

Stochastic processes are just sets of random
variables (RV). Often they are infinite and coupled.
Brownian Motion.
• My value at the next time goes up or down
by a normal random variable.
• Z0 = 0, Zt+1 = Zt + N(0,1)
• Z = cumsum(randn(100,1))
Z is a realization of a Brownian motion
• Often used to model stock prices
normal random variable

variables (RV). Often they are infinite and coupled.
Pólya Urn.
• Consider an urn with 1 purple and 1
green ball, draw a ball at random,
replace it with one of the same
color.
• Z0 = 1, Zt+1 = Zt + B(1, Zt / (t+2))
1 with prob Zt / (t+2)
0 otherwise
Draw ball at random
Put ball back with
another of the same
color

variables (RV). Usually they are infinite and coupled
somehow.
Finite Markov chain & random walk.
Z0 = “state”, Pr(Zt+1 = i | Zt = j) = Pij
• States are indexed by 1, …, n
• The random walk on a graph is a
special Markov chain where
• Random walks on weighted graphs
and finite Markov chains are isomorphic

SIAM REVIEW c⃝ 2015 Society for Industrial and Applied Mathematics
Vol. 57, No. 3, pp. 321–363
PageRank Beyond the Web∗
David F. Gleich†
The PageRank Markov chain and random walk is
another well known instance.
Originally, the random surfer model
• States are web-pages and links between
pages make a directed graph.
• The random surfer is a Markov chain
with prob α follow a random outlink and
with prob (1-α) go to a random page
PageRank can be used for everything from
analyzing the world's most important books to
predicting traffic flow to ending sports arguments.
-JESSICA LEBER, Fast Information.David F. Gleich

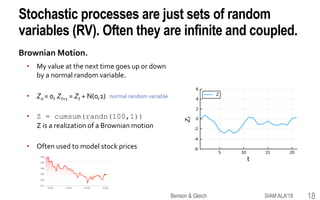
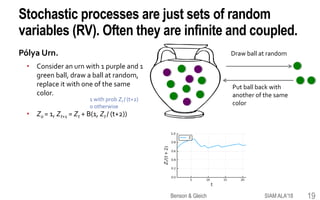
Higher-order Markov chains & random walks are
useful models for many data problems.
Higher order Markov chains & random walks
A second order chain uses the last two states
Z-1 = “state”, Z0 = “another state”
Pr(Zt+1 = i | Zt = j, Zt-1 = k) = Pi,j,k
Simple to understand and turn out to be better models
than standard (first-order) chains in several application
domains [Ching-Ng-Fung 08]
• Traffic flow in airport networks [Rosvall+ 14]
• Web browsing behavior [Pirolli-Pitkow 99; Chierichetti+ 12]
• DNA sequences [Borodovsky-McIninch 93; Ching-Fung-Ng
04]
• Non backtracking walks in networks
[Krzakala+ 13; Arrigo-Gringod-Higham-Noferini 18]
Rosvall et al., Nature Comm., 2014.
A tensor!

Higher-order Markov chains are actually first-order
Markov chains in disguise.
Start with a second-order Markov chain
Consider a new stochastic process
on pairs of variables
Higher-order Markov chains are Markov chains on the product space.

Tensors are a natural representation of transition
probabilities of higher-order Markov chains.
1
3
2
P
Often called transition probability tensors.
[Li-Ng-Ye 11, Li-Ng 14, Chu-Wu 14, Culp-Pearson-
Zhang 17]

A note. Often we use the “second-order” case as
a stand-in for the “general” higher-order case.
Second order Markov chain
Z-1 = “state”, Z0 = “another state”
Pr(Zt+1 = i | Zt = j, Zt-1 = k) = Pijk
General higher-order Markov chain
Pr(Zt+1 = i | Zt = j, Zt-1 = k, …, Zt-m+1 = l) = P(i, j, k, …, l)
Terminology
• Second-order = 2 states of history  3-mode tensor
• mth-order = m states of history  (m+1)-mode tensor
An m+1-mode tensor.

We love stochastic processes because
they give you an intuition and
“physics” about what is happening

A fundamental quantity for stochastic processes is
the fraction of time spent at each state (limiting
distribution).
Consider a stochastic process that goes on infinitely
where each Zj takes a discrete value from a finite set.
We want to know how often are we in a particular state in the long run?
Other fundamental quantities include
• Return times
• Hitting times
(Cesàro limit)

Example limiting distribution with a random walk.
Long time

In the Pólya Urn, the limiting distribution of ball
draws always exists. It can converge to any value.
Thisistheuniformdistribution
We have 1000 samples of the trajectories.

For each realization, the sequence of
random variables
Z1, Z2, …, Zt, Zt+1, …
converges.
It does not converge to a unique value, but
rather can converge to any value.

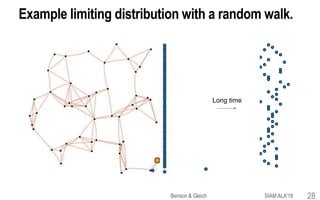
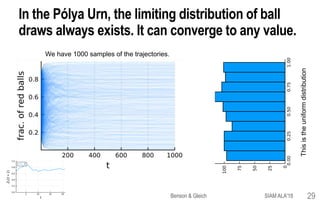
Limiting distributions and stationary distributions
for Markov chains have different properties.
This point is often mis-understood.We want to make sure you get it right!
Limiting distribution 
A stationary distribution  Pk estart converges to p*
Theorem. A finite Markov chain always has a limiting distribution.
Theorem. The limiting distribution is unique if and only if the chain has only a
single recurrent class.
Theorem.A stationary distribution is limt ⟶ ∞ Prob[Zt = i].This is unique if and
only if a Markov chain has a single aperiodic, recurrent class.

States in a finite Markov chain are either recurrent
or transient.
Proof by picture.
Recurrent:
Prob[another visit] = 1
Transient:
Prob[another visit] < 1.
Markov chains ⟺ Dir. graphs
Directed graphs +Tarjan’s
algorithm give the flow among
strongly connected
components. (Block triangular
form.)
Block triangular form
fromTarjan’s algorithm
Strongly connected components
Recurrent states

The fundamental theorem of Markov chains is that
any stochastic matrix is Cesàro summable.
Limiting distribution given start node is P*[:, start] because
Pk gives the k-state transition probability.
Result. Only one recurrent class iff P* is rank 1.
Proof sketch. A recurrent class is a fully-stochastic sub-
matrix. If there are >1 recurrent classes, then P* would be
rank >1 because we could look at the sub-chain on each
recurrent class; if P* is rank 1, then the distribution is the
same regardless of where you start and so “no choice” .
Cesàro summable This always exists!

Stationary distributions are much stronger than
limiting distribution
A stationary distribution  Pk converging to P*
This requires a single aperiodic recurrent class or irreducible & aperiodic
matrix. (There are some funky cases if your chain is really two disconnected,
independent chains.)
We can always make a limiting distribution a stationary distribution.Turn P
into a lazy-Markov chain.
This is automatically aperiodic and doesn’t change the recurrence.

Remember! Tensors are a natural representation
of transition probabilities of higher-order Markov
chains.
1
3
2
P
But the stationary distribution on pairs of states is
still a matrix eigenvector...
[Li-Ng 14] Making the “rank-1 approximation” Xj,k = xjxk gives a
formulation for tensor eigenvectors.

The vector x satisfying Px2 = x is nonnegative and sums to 1.
Thus, x often gets called a limiting distribution.
But all we have done is algebra!
What is a natural stochastic process that has this limiting distribution?

Spacey random walks are stochastic processes
whose limiting distribution(s) lead to such tensor
eigenvectors.
1
3
2
P
1. We are at state Zt = j and want to transition
according to P.
2. However, upon arriving at state Zt = j, we
space out and forget about Zt-1 = k.
3. We still want to do our best, so we choose
state Yt = r uniformly from our history Z1, Z2,
…, Zt
(technically, we initialize having visited each state once).
4. We then follow P pretending that Zt-1 = r.
Stochastic process Z1, Z2, …, Zt, Zt+1, … with states in {1, …,
n}.
Spacey or
space out?
走神
or
心不在焉
According to
David’s students

Spacey random walks are stochastic processes
whose limiting distributions are such tensor
eigenvectors.
10
12
4
9
7
11
4
Zt-1
Zt
Yt
Key insight [Benson-Gleich-Lim 17]
Limiting distributions of this process are tensor eigenvectors of P.
1
3
2
P
Prob(Zt+1 = i | Zt = j, Yt = r) = P(i, j, r).

The main point.
Limiting distributions of the spacey random walk
stochastic process are tensor eigenvectors of P
(we’ll prove this later).

We have to be careful with undefined transitions,
which correspond to zero columns in the tensor.
10
12
4
9
7
11
4
Zt-1
Zt
Yt
1
3
2
P
Prob(Zt+1 = i | Zt = j, Yt = r) = ? P(:, j, r) = 0.
A couple options.
1. Pre-specify a distribution for when P(:, j, r) = 0.
2. Choose a random state from history ⟶ super SRW [Wu-Benson-Gleich 16]

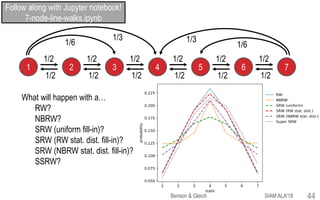
1
2 3
1/2
1/2
1/2
1/2
1/2
1/2
Limiting distribution of
RW is [1/3, 1/3, 1/3].
What about non-backtracking RW?
NBRW disallows going back to where you came from
and re-normalizes the probabilities.
Lim. dist. is still [1/3, 1/3, 1/3], but for far different
reasons.
NBRW is a second-order Markov chain!
What happens with the spacey random walk using the NBRW transition probabilities?
Zero-column fill-in
affects the limiting
distribution and tensor
evec.
Follow along with Jupyter notebook!
3-node-cycle-walks.ipynb

FAQ. Please ask your own questions, too!
1. What’s a spacey random walk, again?
A stochastic process defined by a transition probability tensor.
2. Is the spacey random walk a Markov chain?
No, not in general—the transitions depends on the entire history.
3. Is the limiting distribution of a higher-order MC a tensor e-vec?
No, not in general.
4. Why not just compute the stat. dist. of the higher-order MC?
We are motivating tensor eigenvectors from a stochastic processes view.
5. What is an e-vec with e-val 1 of a transition probability tensor?
It could be the limiting distribution of a spacey random walk.
1
3
2
P

1 2 3
1/2
1/2
Follow along with Jupyter notebook!
7-node-line-walks.ipynb
4 5 6 7
1/2
1/2
1/2
1/2
1/2
1/2
1/2
1/2
1/2
1/2
1/3 1/3
1/61/6
What will happen with a…
RW?
NBRW?
SRW (uniform fill-in)?
SRW (RW stat. dist. fill-in)?
SRW (NBRW stat. dist. fill-in)?
SSRW?

(Not well defined) conjecture.
When the transition probability tensor entries come from
a non-backtracking random walk, the spacey random
walk “interpolates” between the standard random walk
and the non-backtracking one.

Pólya urns are spacey random walks.
Draw random ball.
Put ball back with another of
the same color
This is a second-order spacey
random walk with two states.
Consequently, we know this one must
converge because it’s a Pólya Urn!

But didn’t Pólya Urns have any limiting
distribution? Does this mean that tensor is
interesting? Yes!
Any stochastic vector is a tensor eigenvector
and these are also limiting distributions.

• Compression
• Irreducibility
processes
• FAQ
Act 5. Theory of spacey random
RWs
convergence
• Computation
walks
clustering

Spacey random walks have a number of
interesting properties as well as a number of open
challenges!
Properties
1. Limiting distributions of SRWs are tensor evecs with
eval 1 (proof shortly!)
2. Asymptotically, SRWs are first-order Markov chains.
3. If there are just 2 states, then the SRW converges but
possibly to one of several distributions.
4. If P is sufficiently “regularized”, then the SRW
converges to a unique limiting distribution.
Open problems
• Existence?
• Uniqueness?
• Computation?
1
3
2
P
Note. Spacey random walks
are defined by a stochastic
transition tensor, so these
are all tensor questions!

An informal and intuitive proof that
spacey random walks converge to tensor
eigenvectors
Idea. Let wT be the fraction of time
spent in each state after T ≫ 1 steps.
Consider an additional L steps, T ≫ L ≫
1.Then wT ≈ wT+L if we converge.
1
3
2
P
Long time
wT wT+L
Suppose M(x) = P[wT]m-2 has a unique
stationary distribution, xT.
If the SRW converges, then xT = wT+L,
otherwise wT+L would be different.
Thus, xT = P[wT]m-1 xT ≈ P[wT+L]m-1 xT =
P[xT]m-1 xT = PxT
m-1.
Long time
wT wT+L

To formalize convergence, we need the theory of
generalized vertex reinforced random walks
(GVRRW).
A stochastic process X1, …, Xt, … is a GVRRW if
wT is the fraction of time in each state
FT is the sigma algebra generated by X1, …, XT.
M(wT) is a column stochastic matrix that depends on wT .
[Diaconis 88; Pemantle 92, 07; Benaïm 97]
The classicVRRW is the following
• Given a graph, randomly move to a
neighbor with probability propotional to
how often we’ve visited the neighbor!

(GVRRW).
A stochastic process X1, …, Xt, … is a GVRRW if
wT is the fraction of time in each state
FT is the sigma algebra generated by X1, …, XT.
M(wT) is a column stochastic matrix that depends on wT .
Spacey random walks are GVRRWs with the map M: M(wT) = P[wT]m-2.
[Diaconis 88; Pemantle 92, 07; Benaïm 97]

(GVRRW).
Theorem [Benaïm97] heavily paraphrased
In a discrete GVRRW, the long-term behavior of the occupancy distribution wT
follows the long-term behavior of the dynamical system
To study convergence properties of the SRW, we just need to study the
dynamical system for our map M: M(wT) = P[wT]m-2:
where maps a column stochastic matrix to its Perron vector.

More on how stationary distributions of GVRRWs
correspond to ODEs
THEOREM [Benaïm, 1997] Less Paraphrased
The sequence of empirical observation probabilities ct
is an asymptotic pseudo-trajectory for the dynamical
system
Thus, convergence of the ODE to a fixed point is
equivalent to stationary distributions of the VRRW.
• M must always have a unique stationary distribution!
• The map to M must be very continuous
• Asymptotic pseudo-trajectories satisfy

Spacey random walks converge to tensor
eigenvectors (a more formal proof).
Suppose that the SRW converges.Then we converge to a stationary point.
1
3
2
P
Long time
wT wT+L
Remember the informal proof. All we’ve
done is just formalize this by using the
dynamical system to map behavior!

Corollary. Asymptotically, GVRRWs (including
spacey random walks) act as first-order Markov
chains.
Suppose that the SRW converges to x.
Then

Relationship between spacey random walk
convergence and existence of tensor
eigenvectors.
SRW converges ⇒ existence of tensor e-vec of P with e-val 1.
SRW converges ⇍ existence of tensor e-vec of P with e-val 1.
Apply map f(x) = Pxm-1 satisfies conditions of Brouwer’s fixed point
theorem, so there always exists an x such that Pxm-1 = x.
Furthermore, 𝜆 = 1 is the largest eigenvalue. [Li-Ng 14]
There exists a P for which the SRW does not converge [Peterson 18]

General Open Question.
Under what conditions does the spacey random walk converge?
Peterson’s Conjecture.
If P is a 3-mode tensor, then the spacey random walk converges.
Broader conjecture
There is always a (generalized) SRW that converges to a tensor evec.
What we have been able to show so far.
1. If there are just 2 states, then the SRW converges.
2. If P is sufficiently “regularized”, then the SRW converges.

Almost every 2-state spacey random walk
converges.
[Benson-Gleich-Lim 17]
Special case of 2 x 2 x 2 system...

Almost every 2-state spacey random walk
converges.
Theorem [Benson-Gleich-Lim 17]
The dynamics of almost every
2 x 2 x … x 2 spacey random
walk (of any order) converges
to a stable equilibrium point.
stable
stable
unstable
Things to note…
1. Multiple stable points in above example; SRW could converge to any.
2. Randomness of SRW is “baked in” to initial condition of system.

A sufficiently regularized spacey random walk
converges.
Consider a modified “spacey random surfer” model. At each step,
1. with probability α, follow SRW model P.
2. with probability 1 - α, teleport to a random node.
Equivalent to a SRW on S = αP + (1 – α)J, where J is normalized ones tensor.
Theorem.
If α < 1 / (m – 1),
1. the SRW on S converges [Benson-Gleich-Lim 17]
2. there is a unique tensor x e-vec satisfying Sxm-1 = x [Gleich-Lim-Yu 15]
[Gleich-Lim-Yu 15; Benson-Gleich-Lim 17]

A sufficiently regularized spacey random walk
converges.
The higher-order power method is an algorithm to compute the
dominant tensor eigenvector.
yk+1 = Txk
m-1
xk+1 = yk+1 / || yk+1 ||
Theorem [Gleich-Lim-Yu 15]
If α < 1 / (m – 1), the power method on S = αP + (1 – α)J converges to
the unique vector satisfying Sxm-1 = x.
Conjecture.
If the higher-order power method on P always converges, then
the spacey random walk on P always converges.

Conjecture.
Determining if a SRW converges is PPAD-complete.
Computing a limiting distribution of SRW is PPAD-complete.
Why?
In general, NP-hard to determine if tensor evec for eval 𝜆 [Hillar-Lim 13].
Know evec exists for transition probability tensor P, eval 𝜆 = 1 [Li-Ng 14].
However, no obvious way to compute it.
Similar to other PPAD-complete problems (e.g., Nash equilibria).

General Open Question.
What is the best way to compute tensor eigenvectors?
• Higher-order power method
[Kofidis-Regalia 00, 01; De Lathauwer-De Moor-Vandewalle 00]
• Shifted higher-order power method [Kolda-Mayo 11]
• SDP hierarchies [Cui-Dai-Nie 14; Nie-Wang 14; Nie-Zhang 18]
• Perron iteration [Meini-Poloni 11, 17]
For SRWs, the dynamical system offers another way.
Numerically integrate the dynamical system!
[Benson-Gleich-Lim 17; Benson-Gleich 18]
Equivalent to Perron iteration with Forward Euler & unit time-step.

• Compression
• Irreducibility
processes
• FAQ
RWs
• Computation
Act 6. Applications of spacey
walks
clustering
• New algorithm for computing
evecs

Applications of spacey random walks.
1. Pólya urns are SRWs.
2. SRWs model taxi sequence data.
3. Asymptotics of SRWs for data clustering.
4. Insight for new algorithms to compute tensor eigenvectors.
Stochastic processes offer a new and exciting set of
opportunities and challenges in tensor algorithms. (Us, Slide 10)
66SIAM ALA'18Benson & Gleich

(Review) Pólya urns are spacey random
walks.
Draw random ball.
Put ball back with another of
the same color
This is a second-order spacey
We know it converges by our theory
(every two-state process converges).

Generalized Pólya urns are spacey random walks.
Draw m random balls
with replacement.
Put in new green ball with
probability q(b1, b2, …, bm).
This is a (m-1)-order spacey
We know it converges by our theory
(every two-state process converges).
b1 b2 bm
…

Spacey random walks model sequence data.
Maximum likelihood estimation problem
(most likely P for the SRW model and the observed data).
convex
objective
linear constraints
nyc.gov
[Benson-Gleich-Lim 17]

What is the SRW model saying for this data? Model people by locations.
• A passenger with location k is drawn at random.
• The taxi picks up the passenger at location j.
• The taxi drives the passenger to location i with probability Pi,j,k
Approximate location dist. by history ⟶ spacey random walk.
nyc.gov

• One year of 1000 taxi trajectories in NYC.
• States are neighborhoods in Manhattan.
• Compute MLE P for SRW model with 800 taxis.
• Evaluate RMSE on test data of 200 taxis.
RMSE = 1 – Prob[sequence generated by process]

Spacey random walks are identifiable via this
procedure.
73
Two difficult test tensors from [Gleich-Lim-Yu 15]
1. Generate 80 sequences with 200 transitions each from SRW model
Learn P for 2nd-order SRW, R for 2nd-order MC, P for 1st-order MC
2. Generate 20 sequences with 200 transitions each and evaluate RMSE.
Evaluate RMSE = 1 – Prob[sequence generated by process]
SIAM ALA'18Benson & Gleich

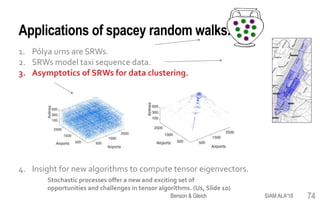
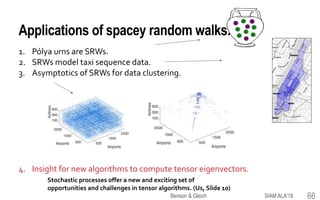
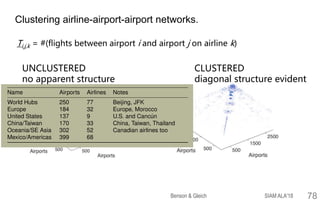
Co-clustering nonnegative tensor data.
Joint work with
Tao Wu, Purdue
Spacey random walks that converge are
asymptotically Markov chains.
• occupancy vector wT converges to w
⟶ dynamics converge to P[w]m-2.
1
3
2
P
2
1 M(wt )
This connects to spectral clustering on graphs.
• Eigenvectors of the normalized Laplacian of a graph are
eigenvectors of the random walk matrix.
• Instead, we compute a stationary distribution w and use
eigenvectors of P = P[w]m-2.
[Wu-Benson-Gleich 16]

We possibly symmetrize and normalize
nonnegative data to get a transition probability
tensor.
[1, 2, …, n] x
[1, 2, …, n] x
[1, 2, …, n]
[i1, i2, …, in1
]x
[j1, j2, …, jn2
]x
[k1, k2, …, kn3
]
If the data is a brick, we symmetrize before
normalization [Ragnarsson-Van Loan 13]
Generalization of
If the data is a symmetric cube,
we can normalize it to get a
transition tensor P.

77
Input. Nonnegative brick of data.
1. Symmetrize the brick (if necessary).
2. Normalize to a stochastic tensor.
3. Estimate the stationary distribution of the spacey random walk
(or super-spacey random walk for sparse data).
4. Form the asymptotic Markov model.
5. Bisect indices using eigenvector of the asymptotic Markov model.
6. Recurse.
Output. Partition of indices.
The clustering methodology.
1
3
2
T

78
Ti,j,k = #(flights between airport i and airport j on airline k)
Clustering airline-airport-airport networks.
UNCLUSTERED
no apparent structure
CLUSTERED
diagonal structure evident

79
“best” clusters
• pronouns & articles (the, we, he, …)
• prepositions & link verbs (in, of, as, to, …)
fun 3-gram clusters
• {cheese, cream, sour, low-fat, frosting, nonfat, fat-free}
• {bag, plastic, garbage, grocery, trash, freezer}
fun 4-gram cluster
• {german, chancellor, angela, merkel, gerhard, schroeder, helmut, kohl}
Ti,j,k = #(consecutive co-occurrences of words i, j, k in corpus)
Ti,j,k,l = #(consecutive co-occurrences of words i, j, k, l in corpus)
Data from Corpus of ContemporaryAmerican English (COCA) www.ngrams.info
Clustering n-grams in natural language.

New framework for computing tensor evecs.
[Benson-Gleich 18]
Our stochastic viewpoint gives a new approach.
We numerically integrate the dynamical system.
Many tensor eigenvector computation algorithms are
algebraic, look like generalizations of matrix power
method, shifted iteration, Newton iteration.
[Lathauwer-Moore-Vandewalle 00, Regalia-Kofidis 00, Li-Ng
14; Chu-Wu 14; Kolda-Mayo 11, 14]
Higher-order power method
Dynamical system
Many known convergence issues!
1. The dynamical system is empirically more robust for
principal evec of transition probability tensors.
2. Can generalize for symmetric tensors & any evec.

[Benson-Gleich 18]
Let Λ be a prescribed map from a matrix to one of its eigenvectors, e.g.,
Λ(M) = eigenvector of M for kth smallest algebraic eigenvalue,
Λ(M) = eigenvector of M for largest magnitude eigenvalue
Suppose the dynamical system converges.Then
New computational framework.
1. Choose a mapΛ
2. Numerically integrate the dynamical system

The algorithm is evolving this system!
The algorithm has a simple Julia code
function mult3(A, x)
dims = size(A)
M = zeros(dims[1],dims[2])
for i=1:dims[3]
M += A[:,:,i]*x[i]
end
return M
end
function dynsys_tensor_eigenvector(A;
maxit=100, k=1, h=0.5)
x = randn(size(A,1)); normalize!(x)
# This is the ODE function
F = function(x)
M = mult3(A, x)
d,V = eig(M) # we use Julia's ordering (*)
v = V[:,k] # pick out the kth eigenvector
if real(v[1]) >= 0; v *= -1.0; end # canonicalize
return real(v) – x
end
# evolve the ODE via Forward Euler
for iter=1:maxit; x = x + h*F(x); end
return x, x'*mult3(A,x)*x
end
Benson & Gleich SIAM ALA'18 83

Empirically, we can compute all the tensor eigenpairs with this approach (including
unstable ones that higher-order power method cannot compute).
tensor is Example 3.6 from [Kolda-Mayo 11]

Why does this work? (Hand-wavy version)
Trajectory of dynamical system for Example 3.6
from Kolda and Mayo [2011]. Color is projection
onto first eigenvector of Jacobian which is +1 at
stationary points. Numerical integration with
forward Euler.
Why does this work?
The eigenvector map shifts
the spectrum around
unstable eigenvectors.

There are tons of open questions with this
approach that we could use help with!
Can the dynamical system cycle?
Yes, but what problems produce this behavior?
Which eigenvector (k) to use?
It really matters 
How to numerically integrate?
Seems like ODE45 does the trick!
SSHOPM -> Dyn Sys?
If SSHOPM converges, can you show the dyn.
sys will converge for some k?
Can you show there are inaccessible vecs?
No clue right now!
Trajectory of dynamical system for Example 3.6
from Kolda and Mayo [2011]. Color is projection
onto first eigenvector of Jacobian which is +1 at
stationary points. Numerical integration with
forward Euler.

• SDP methods can compute all eigenpairs but have
scalability issues [Cui-Dai-Nie 14, Nie-Wang 14, Nie-Zhang
17]
• Empirically, we can compute the same eigenvectors
while maintaining scalability.
tensor is Example 4.11 from [Cui-Dai-Nie 14]

algorithms.
Usually, the properties of these objects are explored algebraically or through
polynomial interpretations.
Our tutorial focused on interpreting the tensor objects stochastically!
A
3
2
1

algorithms.
Hopefully, you should know a little bit about…
And where to look for more info! www.cs.cornell.edu/~arb/tesp
1
3
2
P
• Tensor eigenvectors
• Z-eigenvectors
• Irreducible tensors
• Higher-order Markov chains
• Spacey random walks
• Vertex reinforced random walks
• Dynamical systems for trajectories
• Fitting spacey random walks to data
• Multilinear PageRank models
• Clustering tensors
• And lots of open problems in this area!

Open problems abound!
General Open Questions.
1. What is the relationship between RWs, non-backtracking RWs, and SRWs?
2. Under what conditions does the spacey random walk converge?
3. What is the computational complexity surrounding SRWs?
4. How well does the dynamical system work for computing tensor evecs?
5. How can we use stochastic or dynamical systems views for H-eigenpairs?
6. More data mining applications?
Conjectures.
1. If P is a 3-mode tensor, then the spacey random walk converges.
2. If the HOPM on P always converges, the SRW on P always converges.
3. Determining if a SRW converges is PPAD-complete.
4. Computing a limiting distribution of SRW is PPAD-complete.

Tensor Eigenvectors and Stochastic Processes.
Thanks for your attention!
Today’s information & more. www.cs.cornell.edu/~arb/tesp
Austin R. Benson
http://cs.cornell.edu/~arb
@austinbenson
arb@cs.cornell.edu
David F. Gleich
https://www.cs.purdue.edu/homes/dgleich/
@dgleich
dgleich@purdue.edu

Tensor Eigenvectors and Stochastic Processes

More Related Content

Similar to Tensor Eigenvectors and Stochastic Processes

More from Austin Benson

Recently uploaded

Tensor Eigenvectors and Stochastic Processes