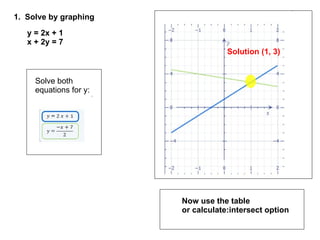
The document provides examples of solving different types of linear systems of equations, including graphing, substitution, and addition methods. It demonstrates setting up and solving systems to find unknown variables from word problems involving gardeners and helpers earning different amounts. The final section defines a linear system as a set of two or more linear equations.

1. Review problems: Solving by using Graphing Substitution Addition Word problem Linear Systems

2. y = 2x + 1 x + 2y = 7 1. Solve by graphing Now use the table or calculate:intersect option Solve both equations for y: Solution (1, 3)

3. x = y - 2 x + y = 18 2. Solve by using the Substitution Method in place of x, substitute (y - 2) NOW SOLVE FOR Y (y - 2) + y = 18 2y - 2 = 18 +2 +2 2y = 20 2 2 y = 10 NOW THAT YOU KNOW THAT y = 10, SUBSTITUTE INTO ONE OF THE ORIGINAL EQUATIONS TO FIND x x = y - 2 x = (10) - 2 x = 8 SOLUTION: (8, 10)

4. 3a - b = 3 a + 3b = 11 3. Solve by using the Addition Method 3a - b = 3 a + 3b = 11 Multiply by 3 to get (-3b) in the first equation which when added together to (+3b) in the second equation will then cancel out. This will allow you to solve for a. 9a - 3b = 9 a + 3b = 11 NOW THAT YOU KNOW THAT a = 2, SUBSTITUTE INTO ONE OF THE ORIGINAL EQUATIONS TO FIND b a + 3b = 11 (2) + 3b = 11 2 + 3b = 11 -2 -2 3b = 9 3 3 b = 3 SOLUTION: a = 2, b = 3 3( ) 10a = 20 10 10 a = 2 +

6. NOW THAT YOU KNOW THAT h = 30, SUBSTITUTE INTO ONE OF THE ORIGINAL EQUATIONS TO FIND g 4g + 4h = 360 4g + 4(30) = 360 4g + 120 = 360 - 120 -120 4g = 240 4 4 g = 60 SOLUTION: Gardeners make $60 an hour, Helpers make $30 an hour 4g + 4h = 360 5g + 6h = 480 -5( ) -20g - 20h = -1800 4h = 120 4 4 h = 30 20g + 24h = 1920 4( )

7. 5. What is a linear system? A set of two or more linear equations