The document discusses key concepts related to ideal and non-ideal solutions including: - Raoult's law describes the vapor pressure of components in an ideal solution. It states the partial vapor pressure of a component is directly proportional to its mole fraction in the liquid. - Deviations from Raoult's law occur for non-ideal solutions where interactions between unlike molecules differ from those between like molecules. - Henry's law describes the solubility of gases in liquids, stating the concentration of a gas is directly proportional to its partial pressure above the solution. 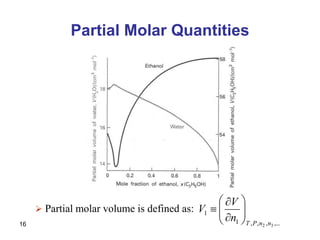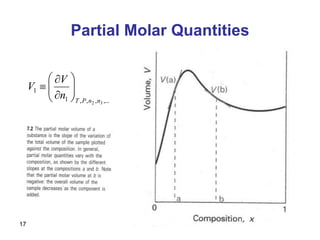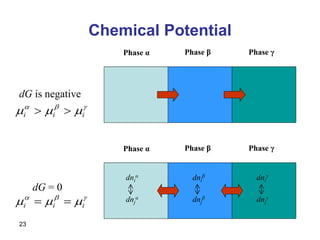- Partial molar quantities allow treatment of non-ideal solutions by considering how properties change with changes in composition.

1. 1
Ideal Solutions
A Solution is any homogeneous phase that contains more
than one component. These components can’t be physically
differentiated.
A Solvent is the component with the larger proportion or
quantity in the solution. A Solute is the component with the
smaller proportion or quantity in the solution.
The idea of Ideal Solutions is used to simplify the study of
the phase equilibrium for solution. The solution is considered
to be ideal when:
 its components are assumed to have similar structures
and sizes, and when
 it represents complete uniformity of molecular forces
(basically attraction forces).

2. 2
Ideal Solutions
When considering a binary system, we are
often interested to study the behavior of that
system in terms of the variables P, T and n.

3. 3
Raoult’s Law
Recall that the vapor pressure is
a measure of the tendency of
the substance to escape from
the liquid.
For an ideal solution composed
of two components (binary
systems) , Raoult’s law relates
between the vapor pressure of
each component in its pure state
(P*) to the partial vapor
pressure of that component
when it is in the ideal solution
(P).

4. 4
Raoult’s Law
To know what partial vapor
pressure a component in a
solution has is important. This
is because it gives you
information about the cohesive
forces in the system.

5. 5
Raoult’s Law
If the solution has partial
vapor pressures that follow:
*
2
2
2
*
1
1
1
P
x
P
P
x
P


then the system is said to obey
Raoult’s law and to be ideal,
taken into consideration T is
fixed for the solvent and
solution.
Examples include:
 Benzene – toluene.
 C2H5Cl – C2H5Br.
 CHCl3 – HClC=CCl2.

6. 6
Application of Raoult’s Law
Problem 5.21:
Benzene and toluene form nearly ideal solutions. If at 300
K, P*(toluene) = 3.572 kPa and P*(benzene) = 9.657 kPa,
compute the vapor pressure of a solution containing 0.60
mole fraction of toluene. What is the mole fraction of
toluene in the vapor over this liquid?

7. 7
Deviations from Raoult’s Law
Deviations from Raoult’s law
occur for nonideal solutions.
Consider a binary system made of
A and B molecules.
Positive deviation occurs when
the attraction forces between A-A
and B-B pairs are stronger than
between A-B. As a result, both A
and B will have more tendency to
escape to the vapor phase.
Examples:
 CCl4 – C2H5OH system.
 n-C6H14 – C2H5OH system

8. 8
Deviations from Raoult’s Law
For a binary system made of A
and B molecules.
Negative deviation occurs when
the attraction force between A-B
pairs is stronger than between A-
A and B-B pairs. As a result, both
A and B will have less tendency
to escape to the vapor phase.
Examples:
 CCl4 – CH3CHO system.
 H2O – CH3CHO system

9. 9
Deviations from Raoult’s Law
Another important
observation is that
at the limits of infinite
dilution, the vapor
pressure of the solvent
obeys Raoult’s law.

10. 10
Henry’s Law
 The mass of a gas (m2)
dissolved by a given
volume of solvent at
constant T is
proportional to the
pressure of the gas (P2)
above and in equilibrium
with the solution.
m2 = k2 P2
where k2 is the Henry’s
law constant.

11. 11
Henry’s Law
 For a mixture of gases
dissolved in a solution.
Henry’s law can be
applied for each gas
independently.
 The more commonly
used forms of Henry’s
law are:
P2 = k’ x2
P2 = k” c2

12. 12
Henry’s Law
 The vapor pressure of a
solute, P2 , in a solution in
which the solute has a mole
fraction of x2 is given by:
P2 = x2 P2*
where P2* is the vapor pressure
of the solute in a pure liquefied
state.
 It is also found that at the
limits of infinite dilution, the
vapor pressure of the solute
obeys Henry’s law.

13. 13
Application of Henry’s Law

14. 14
Partial Molar Quantities
 The method using partial molar quantities enables us to
treat nonideal solutions. In this method we consider the
changes in the properties of the system as its compositions
change by adding or subtracting.
 The thermodynamic quantities, such as U, H, and G, are
extensive functions, i.e. they depend on the amounts of the
components in the system. Also they depend on the P and
T. For example, G = G(P, T, n1, n2, n3, …).

15. 15
In this treatment, the volume is used as starting point to
lead to the thermodynamic functions in terms of partial
molar quantities.
 The volume occupied by H2O molecules added is
dependent on the nature of surrounding molecules.
Partial Molar Volume
water
V = Vw
ethanol
V = Veth
V*(H2O) = 18 mL
Vtot = Vw + 18 mL Vtot = Vw + 14 mL

16. 16
Partial Molar Quantities
 Partial molar volume is defined as:
,...
,
,
,
1
1
3
2 n
n
P
T
n
V
V 











17. 17
Partial Molar Quantities
,...
,
,
,
1
1
3
2 n
n
P
T
n
V
V 











18. 18
Partial Molar Volumes
Exercise:
The partial molar volumes of acetone and
chloroform in a solution mixture in which mole
fraction of chloroform is 0.4693 are 74.166
cm3/mol and 80.235 cm3/mol, respectively. What
is the volume of a solution of a mass 1.000 kg?

19. 19
Chemical Potential
 The chemical potential (μi) of a thermodynamic system
is the amount by which the energy of the system would
change if an additional particle (dni) were introduced.
If a system contains more than one species of particles,
there is a separate chemical potential associated with each
species (μi , μj , …).

20. 20
Chemical Potential
 The chemical potential (μi) of a thermodynamic system
is the amount by which the energy of the system would
change if an additional particle (dni) were introduced.
If a system contains more than one species of particles,
there is a separate chemical potential associated with each
species (μi , μj , …).

21. 21
Chemical Potential
In spontaneous processes at constant T and P, system moves towards a
state of minimum Gibbs energy. (dG < 0)
In the condition of equilibrium at constant T and P, there is no change
in Gibbs energy (dG = 0)

22. 22
Chemical Potential
dG = (μi
β – μi
α) dni
In a spontaneous processes, dG < 0 at constant T and P. dni moves
from phase α to phase β to have negative change in free energy.
The spontaneous transfer of a substance takes place from a region with
a higher μi to a lower μi. The process continues to equilibrium where
dG = 0, and μi and μi become equal.
Phase β
Phase α

23. 23
Chemical Potential
dG is negative
Phase β
Phase α Phase γ
dG = 0
Phase β
Phase α Phase γ





 i
i
i 






 i
i
i 

dni
α
dnj
α
dni
β
dnj
β
dni
γ
dnj
γ

24. 24
Thermodynamic of an Ideal Solution

25. 25
Colligative Properties

26. 26
Colligative Properties

27. 27
Colligative Properties

28. 28
Colligative Properties

29. 29
Colligative Properties

30. 30
Colligative Properties

31. 31
Colligative Properties

32. 32
Colligative Properties

33. 33
Colligative Properties