Download to read offline
Measuring adult mortality using sibling survival
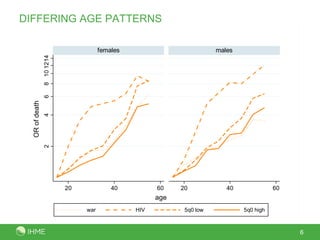
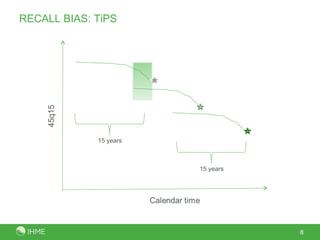
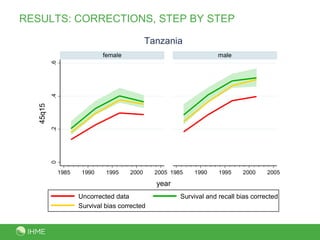
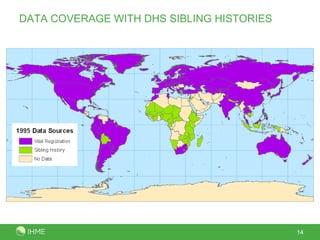
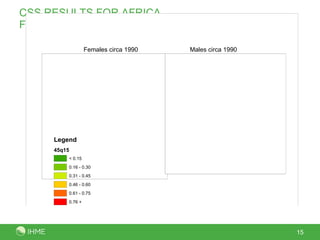
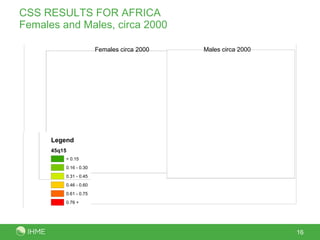
This document presents a new method called the CSS method for measuring adult mortality using sibling survival data from Demographic and Health Surveys. The method uses logistic regression to estimate mortality probabilities while accounting for selection and recall biases. Key results show the CSS method raises estimated mortality rates by an average of 28% after accounting for selection bias, and finds an annual decrease in reported deaths of 1.4-2.1% per year prior to the survey to correct for recall bias. Maps of CSS results for Africa circa 1990 and 2000 are also presented.
More Related Content
Similar to Measuring adult mortality using sibling survival
More from Institute for Health Metrics and Evaluation - University of Washington
![Getting Started with Apache Spark: Big Data Made Simple [Free Meetup]](https://cdn.slidesharecdn.com/ss_thumbnails/apachesparkgettingstarted-260203175547-8361bcc3-thumbnail.jpg?width=640&height=640&fit=bounds)
Measuring adult mortality using sibling survival
- 1. Measuring adult mortalityusing sibling survival A new analytical method and new results for 44 countries, 1974-2006
- 2. SURVEY DATA FORADULT MORTALITY Sibling histories Yield high return of observations per respondent Included in the DHS as a way to measure maternal mortality Respondent asked to report on total number of siblings born to the same mother (“sibship”) Akin to a complete birth history Direct estimates from sibling history data are implausibly low Timaeus & Jasseh (2004) 26 surveys in sub-Saharan Africa Used model life tables to smooth sibling history data Modeled change in age pattern due to HIV
- 3. BIASES IN SIBLINGHISTORY DATA Selection bias: Underrepresentation of high-mortality families Recall bias Deaths omitted from respondent report
- 4. BASICS OF THECSS METHOD Use the observed, generally consistent age patterns of mortality across contexts Consistent patterns in shape of log death rates between the ages of 15 and 60, regardless of level of mortality Use logistic regression to estimate the probability of dying for a given country, sex, age group, and time period Apply the regression model to multiple surveys pooled together Can be applied to: Single population with multiple surveys over time Any grouping of populations where at least some have multiple surveys over time Correct for known selection and recall biases
- 5. LOGISTIC REGRESSION MODEL= survival or death in age group a , in country i for a one-year period of time t = dummy indicators for each age group, a = a set of dummy indicators for country i in the five-year period containing t = a continuous variable representing the time prior to the survey
- 6.
- 7. RECALL BIAS Empiricalwork suggests that respondents omit some sibling deaths TiPS (Time Prior to the Survey) variable Captures difference between deaths reported in the more recent periods of older surveys and the older periods of more recent surveys Exponentiated coefficient approximates the annual incremental reduction in observed probability of death due to omitted deaths Can only be estimated with sufficient overlap of observations from different surveys in the same country year
- 8. RECALL BIAS: TiPS15 years 15 years
- 9. SELECTION BIAS Underrepresentationof high-mortality sibships Families with higher mortality are less likely to be sampled Empirically, larger families have higher mortality Higher death rates in larger sibships means that high mortality sibships are underrepresented and thus bias the estimated rates downward
- 10. SELECTION BIAS: GKWEIGHTS Underrepresentation of high-mortality sibships “ Upweight” observations from high-mortality families: B f /S f is the inverse of the probability of surviving to the time of the survey Multiply the survey sampling weight by the GK weight for final weight; use weights in logistic regression
- 11. RESULTS FROM PRACTICALAPPLICATION Demographic and Health Surveys: Sibling history module 85 surveys 44 countries Respondents: women aged 15-49 Use sibling history data up to 15 years prior to the survey Combine with: 2008 UNAIDS historical HIV seroprevalence data
- 12. RESULTS: CORRECTIONS, STEPBY STEP
- 13. RESULTS: CORRECTIONS Effectof including GK weights – selection bias correction Raise estimated 45 q 15 by an average of 28% Maximum: 66%; minimum: 6% Effect of TiPS – correction for recall bias Males: Annual decrease of 2.1% per year prior to the survey Females: Annual decrease of 1.4% per year prior to the survey Country-specific TiPS not significantly different from average effect, but: Country-specific effects ranged from -0.8% (Mali females) to 7.7% (Madagascar males)
- 14. DATA COVERAGE WITHDHS SIBLING HISTORIES
- 15. CSS RESULTS FORAFRICA Females and Males, circa 1990
- 16. CSS RESULTS FORAFRICA Females and Males, circa 2000
- 17. DISCUSSION: FURTHER RESEARCHMore sibling history data mean more power to estimate and correct for context-specific recall bias TiPS assumes the recall pattern is consistent across settings and over time Gives estimate of “average” recall bias across all surveys Strong assumption From countries with multiple surveys, some evidence that it doesn’t always hold Broader respondent pool needed Male respondents Older ages
Editor's Notes
- #3 The use of survey data to measure adult mortality has been limited, largely because adult deaths are rare events, so large sample sizes are required to generate useful estimates. Sibling histories present a way to capture more information on adult deaths from a survey, especially in settings with a recent history of high fertility. A sibling history captures information on all the siblings of a respondent, including sex, whether alive or dead, current age if alive, and, if the sibling has died, the time of death and age at death. This is essentially a complete birth history of the mother of the respondent. From this information, death rates can be directly computed.
- #5 To address these two sources of bias, we have developed the CSS (Corrected Sibling Survival) method. The CSS method makes use of similarities in age patterns of mortality across contexts. It is a logistic regression model hatestimates the probability of death in a given country, sex, age group and time period (and it requires the data to be in person-year format). The model pools data from multiple surveys – can be applied to a single population with multiple surveys over time or to any grouping of populations where at least some of them have multiple surveys (this is so the recall bias adjustment can be made). The method corrects for selection and recall biases.
- #6 This is the basic logistic regression model. The outcome variable is binary and indicates whether the sibling was alive or died in a particular country, time period, and age group. Ia represents a set of dummy indicators for each five-year age group between ages 15 and 60. This means the age pattern is not assumed to be linear between 15 and 60 but is common across all country and time periods. Note that the model can be extended to allow for different age patterns of mortality, such as those that might be observed due to HIV/AIDS or war, but that is not represented here in this basic notation. It is a set of dummy indicators for country-time periods. The TiPS variable is a continuous variable representing the time prior to the survey of each observation and is what we use to estimate and correct for recall bias.
- #7 The model can be made more flexible to account for different age patterns of mortality. Additional sets of dummy variables can be included that turn on for contexts where the age pattern would be expected to be different. HIV/AIDS is the obvious example, as seen here in the example for Zimbabwe, but other reasons such as conflict/war or high injury rates can also result in different age patterns of mortality.
- #8 The method assumes no omission of deaths at the time of the survey.
- #9 This graph illustrates the concept of recall bias as measured by the time prior to the survey variable. Here is a simplified example of a country with three surveys with sibling histories. From each is obtained a series of estimates of 45q15. For some of the time periods, the estimates from two surveys overlap, such as in this green shaded area here [click to show green area if it’s not on the graph]. The difference between the more recent estimates from the older survey (on top) and the more distal estimates from the newer survey (on bottom) is what is quantified in the TiPS variable. We assume this difference is attributable to recall bias. When the model is used for prediction of age-specific q’s, we set the TiPS variable to zero and thus adjust for recall bias.
- #10 The next adjustment that is needed is an adjustment for selection bias. [Explain here what selection bias is]
- #11 To adjust for selection bias, we apply a set of weights (derived by Gakidou & King, 2006). The GK weights “upweight” observations from high-mortality families. The survival weights are analogous to applying a population sampling weight (the inverse of the probability of selection into the sample). in this case, the weights are the inverse of the probability of surviving to the time of the survey.
- #13 Here is an example of the results for Tanzania showing the raw sibling history data in red. You can see how the estimates change as each adjustment is applied. When the adjustment for selection bias is applied using GK weights, the estimates increase from the red to orange line. When both GK weights and recall bias adjustments are made, the estimates increase from the orange line to green (males) and from orange to yellow (females). The minimal difference between the yellow and green lines in females is due to the zero-survivor adjustment.
- #14 This slide quantifies the adjustment effects.
- #15 Now that known biases have been corrected in these data, estimates of adult mortality from sibling history data are much more plausible. This provides a wealth of empirically based information for countries (especially in Africa) where vital registration data are not available. Here you can see the gap in global coverage for vital registration data in 1995 and the number of countries for which estimates can now be produced from sibling histories – a significant reduction in the data gap.
- #18 TiPS variable assumes constant recall pattern across countries. Evidence suggests this is not true. More data would allow estimation of recall bias that is more context-specific. Including older respondents would mean greater power to estimate stable age patterns to age 60 without pooling so much data.