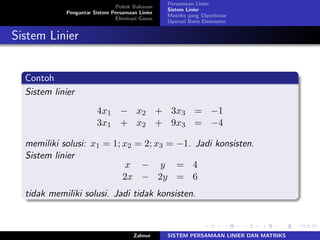
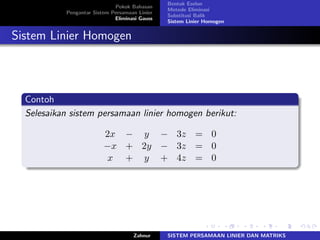
Dokumen tersebut membahas tentang sistem persamaan linier dan matriks. Terdapat penjelasan mengenai pengertian persamaan linier, sistem linier, matriks koefisien dan matriks yang diperbesar, serta operasi baris elementer yang digunakan untuk menyelesaikan sistem persamaan linier.