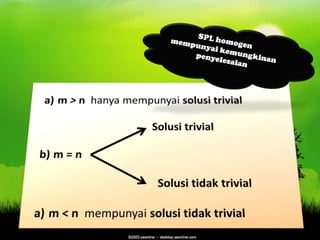
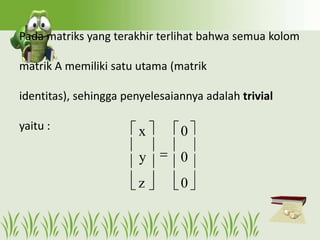
Dokumen tersebut membahas tentang persamaan linear homogen dan penyelesaian sistem persamaan linear homogen (SPLH). SPLH diselesaikan dengan menentukan variabel bebasnya sehingga diperoleh penyelesaian umum berupa vektor kolom yang berisi koefisien variabel bebas.

3. Suatu persamaan
linear disebut
homogen jika semua
bentuk konstantanya
adalah nol.
Dengan bentuk
umum:

4. Amn x = 0
Bentuk umum
matriks

7. Carilah penyelesaian SPL homogen berikut :
x+2y
=0
m=n
-x–2y+z=0
2x + 3 y + z = 0
Jawab :

8. Pada matriks yang terakhir terlihat bahwa semua kolom
matrik A memiliki satu utama (matrik
identitas), sehingga penyelesaiannya adalah trivial
yaitu :
x
0
y
0
z
0

9. Carilah penyelesaian SPL homogen berikut ini :
x– y+ 2z– w=0
2x + y – 2 z – 2w = 0
m=n
x + 2y – 4 z + w = 0
3x
– 3w = 0
Jawab :

10. Dengan memisalkan z =s dan w = t, maka diperoleh
penyelesaian umum :
x
t
y
2s
z
s
w
t
OBE pada SPL Homogen hanya dilakukan pada matrik A
saja, karena tidak akan mempengaruhi hasil perhitungan.