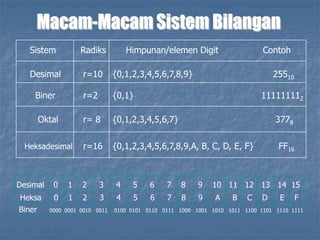
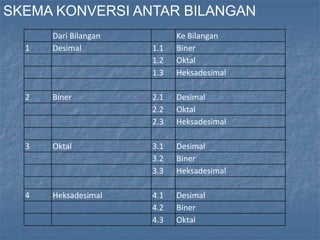
Dokumen ini menjelaskan berbagai sistem bilangan yang digunakan dalam sistem digital, termasuk desimal, biner, oktal, dan heksadesimal. Ia membahas cara representasi bilangan, konversi antar sistem bilangan, serta contoh konversi dari bilangan desimal ke biner, oktal, dan heksadesimal. Selain itu, dokumen ini memberikan rumus dan metode untuk konversi dari satu sistem ke sistem lainnya.

1. Sistem Bilangan
dan
Konversi Bilangan

2. Pendahuluan
 Ada beberapa sistem bilangan yang
digunakan dalam sistem digital. Yang
paling umum adalah sistem bilangan
desimal, biner, oktal dan heksadesimal
 Sistem bilangan desimal merupakan
sistem bilangan yang paling familier
dengan kita karena berbagai
kemudahannya yang kita pergunakan
sehari – hari.

3. REPRESENTASI BILANGAN
 Dinyatakan dengan sign, bilangan magnitude dan posisi
titik radiks.
 Titik radiks memisahkan bilangan bulat dan pecahan.
 Penggunaan titik radiks berkaitan dengan jajaran
bilangan yang dapat ditampung oleh komputer.
 Representasi Fixed-point : titik radiks selalu pada posisi
tetap.
 Representasi Floating-point :
a = m x r e
r = radiks, m = mantissa, e = eksponen
 Untuk menyatakan bilangan yang sangat besar atau
sangat kecil, dengan menggeser titik radiks
dan mengubah eksponen untuk mempertahankan
nilainya.

4.  Contoh:
 Bilangan desimal:
5185.6810 = 5x103 + 1x102 + 8x101 +
5x100 + 6 x 10-1 + 8 x 10-2
= 5x1000 + 1x100 + 8x10 + 5 x 1 +
6x0.1 + 8x0.01
 Bilangan biner (radiks=2, digit={0, 1})
100112 = 1  16 + 0  8 + 0  4 + 1 
2 + 1  1 = 1910
101.0012 = 1x4 + 0x2 + 1x1 + 0x.5 + 0x.25
+ 1x.125 = 5.12510

5. SISTEM BILANGAN
BINER (radiks / basis 2)
Notasi : (n)2
Simbol : angka 0 dan 1
OKTAL (radiks / basis 8)
Notasi : (n)8
Simbol : angka 0, 1, 2, 3, 4, 5, 6, 7
DESIMAL (radiks / basis 10)
Notasi : (n)10
Simbol : angka 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
HEKSADESIMAL (radiks / basis 16)
Notasi : (n)16
Simbol : angka 0,1,2,3,4,5,6,7,8,9,A,B, C,D,E,F

6. Sistem Radiks Himpunan/elemen Digit Contoh
Desimal r=10
r=2
r=16
r= 8
{0,1,2,3,4,5,6,7,8,9} 25510
Biner
{0,1,2,3,4,5,6,7} 3778
{0,1} 111111112
{0,1,2,3,4,5,6,7,8,9,A, B, C, D, E, F} FF16
Oktal
Heksadesimal
Biner 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
Heksa 0 1 2 3 4 5 6 7 8 9 A B C D E F
Desimal 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

7. Dari Bilangan Ke Bilangan
1 Desimal 1.1 Biner
1.2 Oktal
1.3 Heksadesimal
2 Biner 2.1 Desimal
2.2 Oktal
2.3 Heksadesimal
3 Oktal 3.1 Desimal
3.2 Biner
3.3 Heksadesimal
4 Heksadesimal 4.1 Desimal
4.2 Biner
4.3 Oktal
SKEMA KONVERSI ANTAR BILANGAN

8. 1.1 Konversi Bilangan Desimal ke
Biner
 Konversi bilangan desimal bulat ke
bilangan Biner: Gunakan pembagian dgn
2 secara suksesif sampai sisanya = 0.
Sisa-sisa pembagian membentuk
jawaban, yaitu sisa yang pertama akan
menjadi least significant bit (LSB) dan
sisa yang terakhir menjadi most
significant bit (MSB).

9.  Contoh: Konersi 17910 ke biner:
 179 / 2 = 89 sisa 1 (LSB)
 / 2 = 44 sisa 1
 / 2 = 22 sisa 0
 / 2 = 11 sisa 0
 / 2 = 5 sisa 1
 / 2 = 2 sisa 1
 / 2 = 1 sisa 0
 / 2 = 0 sisa 1 (MSB)
  17910 = 101100112

 MSB LSB

10. 1.2 Konversi Bilangan Desimal ke
Oktal
 Konversi bilangan desimal bulat ke
bilangan oktal: Gunakan pembagian dgn
8 secara suksesif sampai sisanya = 0.
Sisa-sisa pembagian membentuk
jawaban, yaitu sisa yang pertama akan
menjadi least significant bit (LSB) dan
sisa yang terakhir menjadi most
significant bit (MSB).

11.  Contoh: Konersi 17910 ke oktal:
 179 / 8 = 22 sisa 3 (LSB)
 / 8 = 2 sisa 6
 / 8 = 0 sisa 2 (MSB)
  17910 = 2638

 MSB LSB

12. 1.3 Konversi Bilangan Desimal ke
Hexadesimal
 Konversi bilangan desimal bulat ke bilangan
hexadesimal: Gunakan pembagian dgn 16
secara suksesif sampai sisanya = 0. Sisa-
sisa pembagian membentuk jawaban, yaitu
sisa yang pertama akan menjadi least
significant bit (LSB) dan sisa yang terakhir
menjadi most significant bit (MSB).

13.  Contoh: Konersi 17910 ke hexadesimal:
 179 / 16 = 11 sisa 3 (LSB)
 / 16 = 0 sisa 11 (dalam
bilangan hexadesimal berarti B)MSB
  17910 = B316

 MSB LSB

14. Konversi Radiks-r ke desimal
 Rumus konversi radiks-r ke desimal:
 Contoh:
 11012 = 123 + 122 + 120
= 8 + 4 + 1 = 1310
 5728 = 582 + 781 + 280
= 320 + 56 + 16 = 39210
 2A16 = 2161 + 10160
= 32 + 10 = 4210






1
n
n
i
i
i
r r
d
D

15.  Uraikan masing-masing digit bilangan
biner kedalam susunan radik 2
2.1 Konversi Bilangan Biner
ke Desimal






1
n
n
i
i
i
r r
d
D
1011012 = 125 + 123 + 122 + 120
= 32 + 8 + 4 + 1 = 4510

16. 2.2 Konversi Bilangan Biner
ke Oktal
Untuk mengkonversi bilangan biner ke
bilangan oktal, lakukan
pengelompokan 3 digit bilangan biner
dari posisi LSB sampai ke MSB

17.  Contoh: konversikan 101100112 ke
bilangan oktal
 Jawab : 10 110 011
 2 6 3
 Jadi 101100112 = 2638

18. 2.3 Konversi Bilangan Biner
ke Hexadesimal
Untuk mengkonversi bilangan biner ke
bilangan hexadesimal, lakukan
pengelompokan 4 digit bilangan biner
dari posisi LSB sampai ke MSB

19.  Contoh: konversikan 101100112 ke
bilangan oktal
 Jawab : 1011 0011
 B 3
 Jadi 101100112 = B316

20.  Uraikan masing-masing digit bilangan
biner kedalam susunan radik 8
3.1 Konversi Bilangan Oktal
ke Desimal






1
n
n
i
i
i
r r
d
D
12348 = 183 + 282 + 381 + 480
= 4096 + 128 + 24 + 4 = 425210

21. 3.2 Konversi Bilangan Oktal
ke Biner
Sebaliknya untuk mengkonversi Bilangan
Oktal ke Biner yang harus dilakukan
adalah terjemahkan setiap digit bilangan
oktal ke 3 digit bilangan biner

22.  Contoh Konversikan 2638 ke bilangan
biner.
 Jawab: 2 6 3
 010 110 011
 Jadi 2638 = 0101100112 Karena 0 didepan
tidak ada artinya kita bisa menuliskan
101100112

23. 3.3 Konversi Bilangan Oktal
ke Heksadesimal

24. Konversi Bilangan Hexadesimal
ke Biner
Sebaliknya untuk mengkonversi Bilangan
Hexadesimal ke Biner yang harus
dilakukan adalah terjemahkan setiap digit
bilangan Hexadesimal ke 4 digit bilangan
biner

25.  Contoh Konversikan B316 ke bilangan
biner.
 Jawab: B 3
 1011 0011
 Jadi B316 = 101100112

26. Tugas
Konversikan Bilangan di Bawah ini
 8910 = ……16
 3678 = ……2
 110102 = ……10
 7FD16 = ……8
 29A16 = ……10
 1101112 = …….8
 35910 = ……2
 4728 = ……16

27. Daftar Pustaka
 Digital Principles and Applications, Leach-
Malvino, McGraw-Hill
 Sistem Diugital konsep dan aplikasi,
freddy kurniawan, ST.
 Elektronika Digiltal konsep dasar dan
aplikasinya, Sumarna, GRAHA ILMU