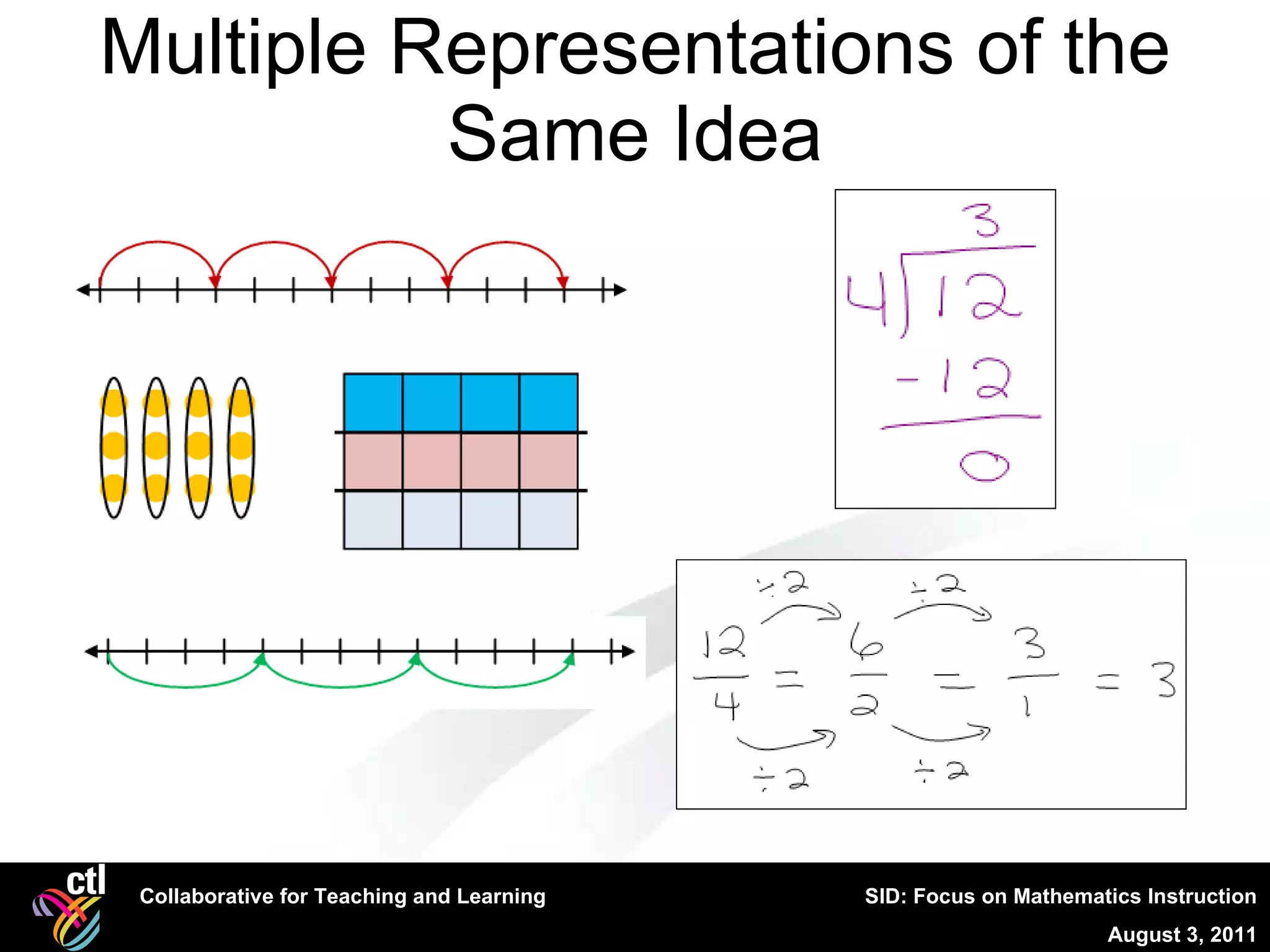
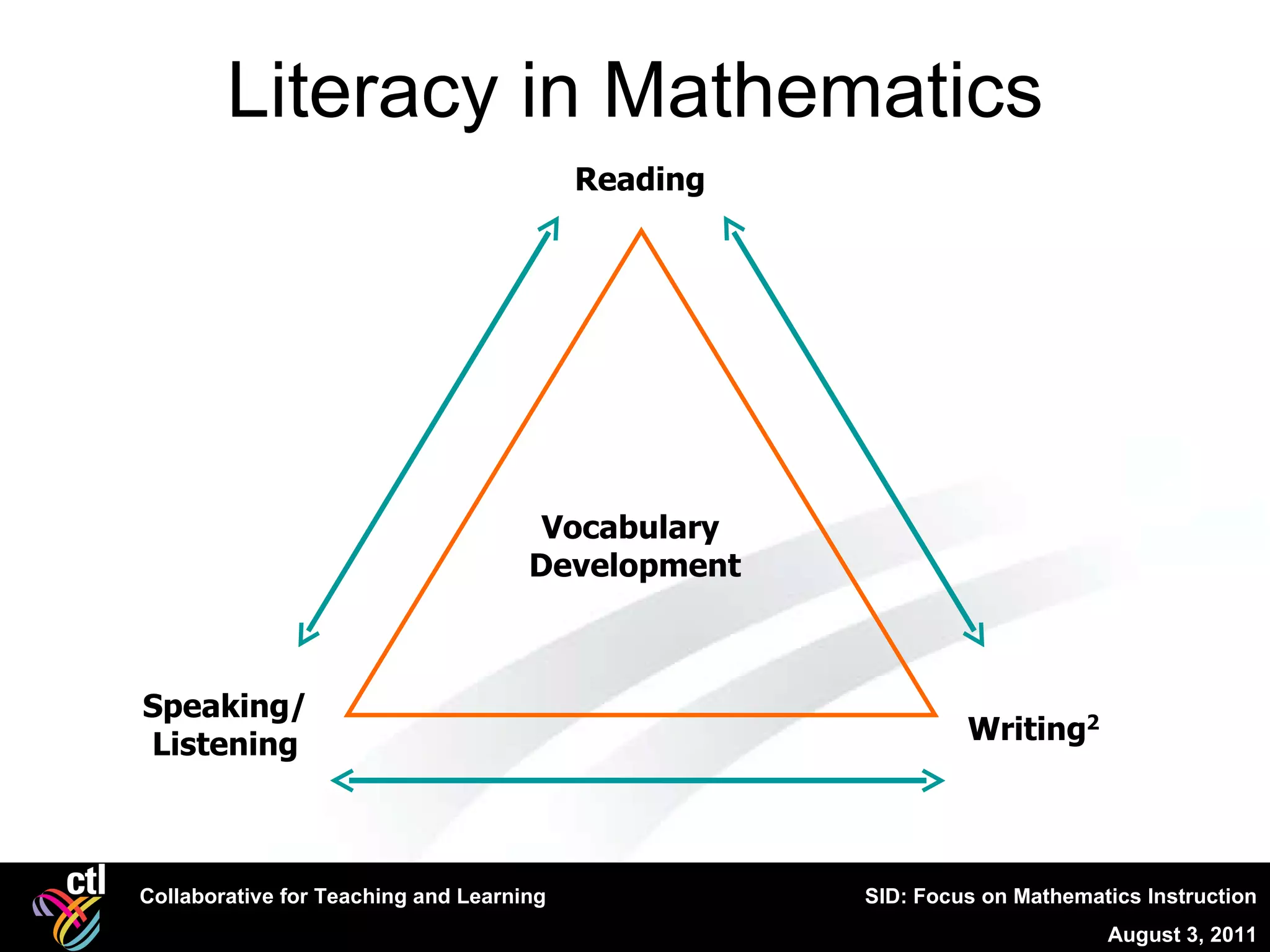
1. The mathematics summit focused on developing mathematical literacy in classrooms through instructional strategies like discourse, multiple representations, and connecting standards to classroom practice. 2. The agenda included lessons on vocabulary, routines, classroom discourse, analyzing standards, and using representations and manipulatives to develop conceptual understanding. 3. The project aims to provide teachers support through coaching, analyzing student work, and discussions to help develop curriculum and instruction aligned to new standards.

1. Mathematics Summit Southern Indiana Deanery: Focus on Mathematics Instruction

2. Standards for the Day Deepen understanding of creating a mathematically literate classroom Apply a variety of strategies to support and promote the learning of mathematics Promote own and others’ learning through community conversation, collaboration and reflection

3. Agenda DAY I Grant Overview/Introduction Mini-lesson: connecting Mathematical Literacy Vocabulary Development Routines- GOs and Word Walls Developing Classroom Discourse for Deeper Understanding DAY II Analysis of New Common Core State Standards Using Multiple Representations to Develop Deeper Understanding Using Number lines and manipulatives to support conceptual understanding

4. Introductions Introduce yourself, let us know School, grade, experience (if you want) Something interesting you did or are going to do this summer Anything else you want to share! Be sure you have a name tag and have signed in

5. Project Overview- Part 1 6 days of PD during the year Developing curriculum, instructional practices, and resources that support mathematics instruction Provide teachers with feedback through: coaching, analysis of student work, & informal discussion

6. Project Overview- Part 2 2 days of summer training 1 st Semester: 1 cadre day to be held at a school, during September/early October 2 x 1 day grade level coaching for each group (5/6, 7/8), late October/early November 2 nd Semester: 1 cadre day, during late February/early March Distance support for mathematics teachers

7. Take a few moments to compare the NCTM Processes and CCSS Practice Standards Guiding Questions: How are the processes and practices similar? How do they differ? What do the new practices mean for my instruction? Indiana Transition Info

8. NCTM Standards for Mathematics Content Number Algebra Geometry & Measurement Probability & Statistics Process Problem Solving Reasoning & Proof Communication Connections Representations CTL, Mathematical Literacy

9. Instructional Programs Pre K-12 Should Enable All Students To: Organize & consolidate their mathematical thinking through communication Communicate their mathematical thinking coherently and clearly to peers, teachers, and others Analyze & evaluate the mathematical thinking & strategies of others Use the language of mathematics to express mathematical ideas precisely ( NCTM Standards, p. 269) CTL, Mathematical Literacy

10. CCSS Content for Mathematics Number and Operations k – 12 Algebra k – 5, 9 – 12 Measurement & Data k – 5 Geometry k – 12 Expressions & Equations 6 – 8 Proportionality 6 – 7 Statistics & Probability 6 – 12 Functions 8 – 12 Modeling 9 – 12 CCSS Mathematics Standards

11. CCSS Practices for Mathematics Make sense of problems/persevere in solving them. Reason abstractly and quantitatively. Construct viable arguments and critique the reasoning of others. Model with mathematics. Use appropriate tools strategically. Attend to precision. Look for and make use of structure. Look for and express regularity in repeated reasoning .

12. Take a few moments to compare the NCTM Processes and CCSS Practice Standards Guiding Questions: How are the processes and practices similar? How do they differ? What do the new practices mean for my instruction?

13. "The ability to read, listen, think creatively, and communicate about problem situations, mathematical representations, and the validation of solution will help students to develop and deepen their understanding of mathematics." (NCTM Standards, p. 80)

14. What are the necessary ingredients to communicate mathematics effectively?

15. “ Students should be encouraged to increase their ability to express themselves clearly and coherently. As they become older, their styles of argument and dialogue should more closely adhere to established conventions, and students should become more aware of, and responsive to, their audience. The ability to write about mathematics should be particularly nurtured across the grades .”

16. “ Students should be encouraged to increase their ability to express themselves clearly and coherently. As they become older, their styles of argument and dialogue should more closely adhere to established conventions, and students should become more aware of, and responsive to, their audience. The ability to write about mathematics should be particularly nurtured across the grades .”

17. “ Students should be encouraged to increase their ability to express themselves clearly and coherently. As they become older, their styles of argument and dialogue should more closely adhere to established conventions, and students should become more aware of, and responsive to, their audience. The ability to write about mathematics should be particularly nurtured across the grades.”

18. Mathematics as a Language Includes Elements, Notation, and Syntax Is the language (science) of patterns and change Is a way of thinking about the world Is a necessary ingredient for developing & demonstrating understanding – both oral & written language ( Sensible, Sense-Making Mathematics , by Steve Leinwand ) CTL, Mathematical Literacy

19. How do we represent in mathematics?

20. CTL, Mathematical Literacy How many ways can we say or represent 12 ÷ 4 mathematically?

21. Multiple Representations of the Same Idea

22. Literacy in Mathematics Vocabulary Development Reading Writing 2 Speaking/ Listening

24. “ Research in the past ten years reveals that vocabulary knowledge is the single most important factor contributing to reading comprehension.” Teaching Reading in the Content Areas , Billmeyer & Barton

25. “ Reading mathematics means decoding and comprehending not only words but mathematical signs, symbols, and diagrams/graphs.” “ Consequently, students need to learn the meaning of each symbol and to connect each symbol, the idea that the symbol represents, and the written or spoken word(s) that correspond to that idea.” (McREL, Teaching Reading in Mathematics)

26. The Precise Language of Mathematics CTL, Mathematical Literacy Graphic Organizers that allow for multiple representations/interactions Frayer Model, VVWA, Alphablocks, Foldables

27. Gradual Release Model I Do, You Watch I Do, You Help You Do, I Help You Do, I Watch Extended Scaffolding I Suggest, You Do You Decide to Do

28. CTL, Mathematical Literacy “ The Mathematical Communication Standard is closely tied to problem solving and reasoning. Thus as students’ mathematical language develops, so does their ability to reason and solve problems. Additionally, problem-solving situations provide a setting for the development & extension of communication skills & reasoning ability.” (NCTM Standards, pp 80)

29. Something that squared with your beliefs Something going ‘round and ‘round in your head Three points you want to remember Exit Slip

30. Developing Discourse in the Classroom Choose an article to read We are using two reading strategies as we read: Text coding Margin notes You have 30 minutes to read the article

31. Sample Margin Notes

32. Text Coding !- Important Idea ?- I have a question - I disagree with - agrees with my thinking

33. Discourse Discussion In similar article groups discuss the main idea of the article and the appropriate guiding questions In mixed groups we are going to have a Café Conversation

34. Something that squared with your beliefs Something going ‘round and ‘round in your head Three points you want to remember Exit Slip