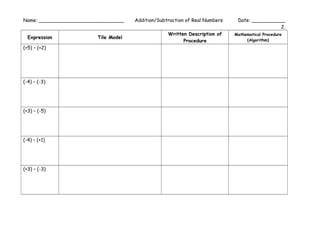
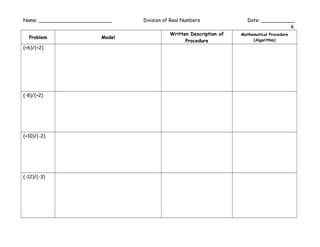
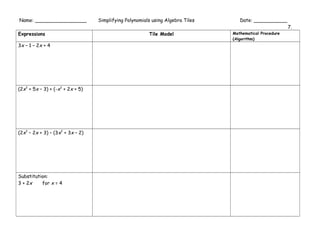
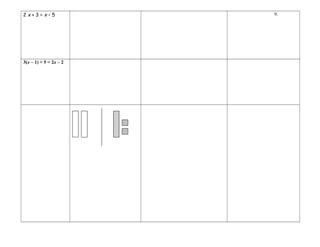
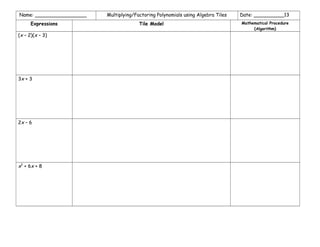
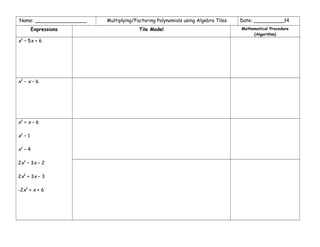
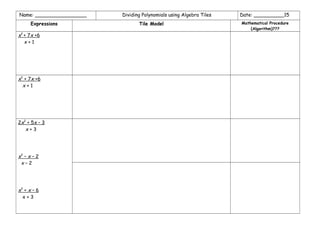
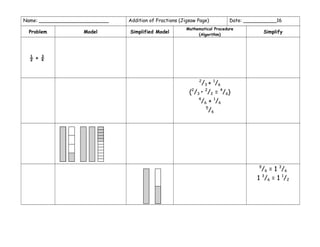
The document outlines various mathematical procedures and algorithms related to addition, subtraction, multiplication, division, and simplification of real numbers and polynomials using algebra tiles. It includes different expressions, equations, and specific step-by-step descriptions for modeling and solving mathematical problems. The document serves as a resource for understanding and applying mathematical concepts with tile models.

1. Name: ____________________________
Expression
(+3) + (+1)
(-2) + (-1)
(+3) + (-1)
(+3) + (-4)
Tile Model
Addition/Subtraction of Real Numbers
Written Description of
Procedure
Date: ___________
1.
Mathematical Procedure
(Algorithm)

2. Name: ____________________________
Expression
(+5) – (+2)
(-4) – (-3)
(+3) – (-5)
(-4) – (+1)
(+3) – (-3)
Tile Model
Addition/Subtraction of Real Numbers
Written Description of
Procedure
Date: ___________
2.
Mathematical Procedure
(Algorithm)

3. Name: ________________________
Problem
(+2)(+3)
(+3)(-4)
(-2)(+3)
(-3)(-1)
Model
Multiplication of Real Numbers
Written Description of
Procedure
Date: ___________
3.
Mathematical Procedure
(Algorithm)

4. Name: ________________________
Problem
(+6)/(+2)
(-8)/(+2)
(+10)/(-2)
(-12)/(-3)
Model
Division of Real Numbers
Written Description of
Procedure
Date: ___________
4.
Mathematical Procedure
(Algorithm)

5. Name: ____________________
Expression
3(x + 2)
3(x – 4)
-2(x + 2)
-3(x – 2)
Simplifying the Distributive Property using Algebra
Tiles
Tile Model
Written Description of Procedure
Date: ___________
5.
Mathematical Procedure
(Algorithm)

6. Name: _________________
Expressions
2x + 3
4x – 2
2x + 4 + x + 2
- 3x + 1 + x + 3
Simplifying Polynomials using Algebra Tiles
Tile Model
Date: ___________
6.
Mathematical Procedure
(Algorithm)

7. Name: _________________
Simplifying Polynomials using Algebra Tiles
Date: ___________
7.
Expressions
3x – 1 – 2x + 4
(2x2 + 5x – 3) + (-x2 + 2x + 5)
(2x2 – 2x + 3) – (3x2 + 3x – 2)
Substitution:
3 + 2x
for x = 4
Tile Model
Mathematical Procedure
(Algorithm)

8. Name: ____________________
Equation
x+2=3
-5 = 2x
1
= −x
2
x
= −2
3
Solving/Modeling Equations using Algebra Tiles
Tile Model
Written Description of Procedure
Date: ___________ 8.
Mathematical Procedure
(Algorithm)

9. 2x+3=x–5
3(x – 1) + 5 = 2x – 2
9.

10. Name: _________________
Equation
Solving/Modeling Equations using Algebra Tiles (Jigsaw Page 1)
Tile Model
Written Description of Procedure
Date: _________ 10.
Mathematical Procedure
(Algorithm)
2x = -8
One negative x is equal to 5
2. Take the opposite of each
side of the equation
3. One x is equal to five
negative units
1.
3x = 2 + x
-x
-x
2x = 2
÷2 ÷ 2
x = 1

11. Name: _________________
Equation
Solving/Modeling Equations using Algebra Tiles (Jigsaw Page 2) Date: ___________11
Tile Model
Written Description of Procedure
Mathematical Procedure
(Algorithm)
2x + 1 = 5
1. Three negative x’s and two units are
same as 5
2. Subtract two units from each side
of the equation
3. Divide both sides of the equation
into two equal groups
4. Flip both sides of the equation to
make them opposites
5. One x is equal to one negative unit
2x-3 =2+x
-x
-x
x–3= 2
+3 +3
x = 5

12. Name: _________________
Expressions
(12)(13) = (10+2)(10+3)
(x + 2)(x + 3)
(x – 1)(x +4)
(x + 2)(x – 3)
Multiplying Polynomials using Algebra Tiles
Tile Model
Date: __________12
Mathematical Procedure
(Algorithm)

13. Name: _________________
Expressions
(x – 2)(x – 3)
3x + 3
2x – 6
x2 + 6x + 8
Multiplying/Factoring Polynomials using Algebra Tiles
Tile Model
Date: __________13
Mathematical Procedure
(Algorithm)

14. Name: _________________
Expressions
x 2 – 5x + 6
x2 – x – 6
x2 + x – 6
x2 – 1
x2 – 4
2x2 – 3x – 2
2x2 + 3x – 3
-2x2 + x + 6
Multiplying/Factoring Polynomials using Algebra Tiles
Tile Model
Date: __________14
Mathematical Procedure
(Algorithm)

15. Name: _________________
Expressions
x2 + 7x +6
x+1
x2 + 7x +6
x+1
2x2 + 5x – 3
x+3
x2 – x – 2
x–2
x2 + x – 6
x+3
Dividing Polynomials using Algebra Tiles
Tile Model
Date: __________15
Mathematical Procedure
(Algorithm)???

16. Name: _______________________
Problem
Model
Addition of Fractions (Jigsaw Page)
Simplified Model
Date: ___________16
Mathematical Procedure
(Algorithm)
Simplify
½+¾
2
/3 + 1/6
(2/3 • 2/2 = 4/6)
4
/6 + 1/6
5
/6
9
/6 = 1 3/6
1 3 / 6 = 1 1/ 2