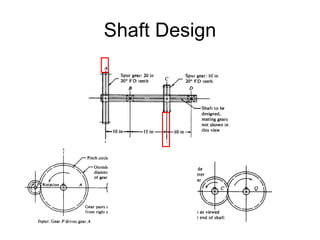
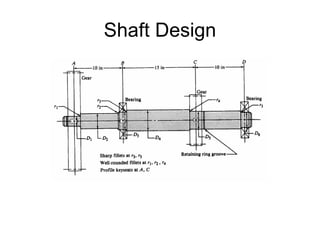
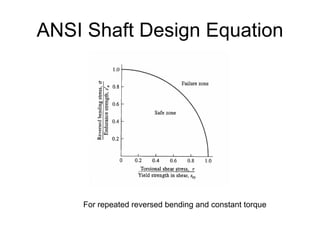
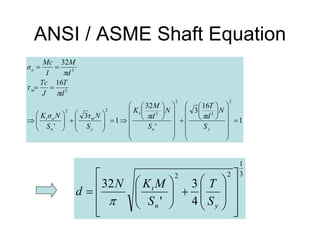
The document discusses shaft design and analysis. It provides information on forces acting on shafts, developing shear and moment diagrams, stress concentration factors, fatigue failure criteria, and the ANSI shaft design equation. An example is presented to demonstrate calculating torque and forces on a shaft, developing shear and moment diagrams, and determining the shaft diameter at critical locations using the design equation.

1. Shaft Design
ENTC 463
Mechanical Design Applications II

2. Next Thursday
4/3/2008
Meet @ Thompson 009B
ENTC 463
Mechanical Design Applications II
Allen to Hagan –2:20 to 3:00 PM
Higginbotham to Winniford–3:00 to 3:35 PM

3. ATTENTION: MMET Students, the IAC members would like to meet YOU on April 11th! WHO?IAC MembersWHAT?Meet and GreetWHERE?510, 5th Floor Rudder TowerWHEN?April 11th3:30-5:00pmWHY?They will also be available to review your resume and help you improve it for potential employers. Please sign up with Courtney in THOM 117Deadline to sign up is April 8th.

4. MMET IAC Meeting
April 11th2008
STUDENTS NEEDED!!
MMET Majors ONLY
Come join us for the 2008 Spring IAC Meeting
Great DOOR PRIZES!
I-POD NANO and much more!
(Must Be Present to Win)
Sign up with Courtney in THOM 117

5. ENTC 463
•Lab 3 Due 4/10
•Homework HW 12 Due 4/15
–Chapter 12 –2, 4, 25, 27

6. Shafts
•Mott, Chapter 12
•Why use shaft?
–To transmit power
•Shaft geometry
–Cylinder, bar, beam (length and diameter)
•Load acting on shaft
–Torsion (shear stress)
–Bending (normal stress)

7. Shaft Design

8. Shaft Design

9. Shaft Design
•Given required power to be transmitted
–Calculate torque,
–Calculate forces,
–Calculate stresses (if geometry is known),
–Select material
•Given required power to be transmitted
–Calculate torque,
–Calculate forces,
–Determine shaft diameter (if the material is known)

10. Shaft Design Procedure
1.Develop the free body diagram; model the various machine elements mounted on the shaft in terms of forces and torques
2.Develop the shear and moment diagram; identify bending moment (leads to normal stress) and torque (leads to shear stress)
3.Identify critical locations for stress analysis; calculate stresses (known diameter)
4.Determine diameter or select material based on failure theories

11. Forces Acting on Shaft
•Forces due to gear (spur gear) gear) (helical tantan263000 ψφ txtrtWWWWDTWnhpT= = = =

12. Forces due to Gears

13. Forces Acting on Shaft
•Forces due to chain and sprocket θθ sincos222ccyccxBBAAcFFFFDTDTDTF= = ===

14. Forces Acting on Shaft
•Forces due to V-belt and sheave20.2pulley andbelt flat For 25.121DTFDTFFFFBBB≈ ≈ −=

15. Example
•A chain is transmitting 100 kW with the chain speed at 6000 rpm and V = 50 m/s. The shaft material is AISI 1040 cold drawn. Determine the shaft diameter required.

16. Shaft Design Considerations
•Stress Concentration (fillet or key seat)
1.5 < Kt < 2.5
•Combined tangential and radial load (3-D)
–Two shear and moment diagramsWtWr22yzxyyMMM+= xz
y

17. Stress Concentration
•Keyseats
–Kt = 2.0 for profile keyseat
–Kt = 1.6 for sled keyseat
•Shoulder fillets
–Kt = 2.5 for sharp fillet
–Kt = 1.5 for well-rounded fillet
•Retaining ring grooves
–Kt = Kt= 3.0, or
–Increase diameter by 6%

18. Forces Acting on A Shaft

19. Shear and Moment DiagramsFrom bottom look upFront view

20. Shaft Design/Analysis Example()() () 31223122223223223313232321616: ⎟⎟⎟ ⎠ ⎞ ⎜⎜⎜⎝ ⎛ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≥ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +≥ ≤+ ≤+−−++ ≤− yyyyyySTSMNdTMSNdNSTMdNSTMMdTMMdNSMSST πππππσσ () () () () () ()2232212232213434162216221632232642TMMdTMMddTddTJTcdMddMIMcxyxxxyxxxyx+−=+⎟⎠ ⎞ ⎜⎝ ⎛−= ++=+⎟⎠ ⎞ ⎜⎝ ⎛+= === === πτσσσπτσσσππτππσ
Is this correct ?

21. Fatigue Failure Criterion
•Cyclic loading due to shaft rotation
–Find mean and alternating stresses
–Construct Mohr’s circles for mean stress and alternating stress
–Derive effective mean and alternating stresses (based on MSST or DET)
–Use Soderbergor Goodman for design and analysis

22. Fatigue Failure of Shaft3316032dTdMxyyx πτσπσ = = ±= 31600:MeandTmxymymx πτσσ = = = 0032:gAlternatin3= = = mxymyaxdM τσπσ NSSKdMdTymnatam1' ' ' :Soderberg32' 32' 33=+ = = σσπσπσ 1' :sionsteady tor and bending reversedfully for equation ANSI/ASME22=⎟⎟ ⎠ ⎞ ⎜⎜⎝ ⎛ +⎟⎟⎠⎞ ⎜⎜⎝ ⎛ ysmnaSτSσ

23. ANSI Shaft Design Equation
For repeated reversed bending and constant torque

24. ANSI/ASME Shaft Equation1' :sionsteady tor and bending reversedFully 22=⎟⎟⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ysmnaSτSσ1' 1' 1' :factorsafety Consider 222222=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⇒=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⇒ =⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ysmnaysmnaysmnaSNτSNσNSτNSσSτSσ

25. ANSI / ASME Shaft Equation13' 31' 1' :n)for torsioshear (pure DET Use222222=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⇒ ⎟⎟⎟⎟ ⎠ ⎞ ⎜⎜⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⇒=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ymnaymnaysmnaSNτSNσSNτSNσSNτSNσ13' 13' :ionconcentrat stressConsider 2222=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⇒=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ymnatymnaSNτSNσKSNτSNσ

26. ANSI / ASME Shaft Equation1163' 3213' 163223232233= ⎟⎟⎟⎟ ⎠ ⎞ ⎜⎜⎜⎜ ⎝ ⎛ ⎟⎠ ⎞ ⎜⎝ ⎛ + ⎟⎟⎟⎟ ⎠ ⎞ ⎜⎜⎜⎜ ⎝ ⎛ ⎟⎠ ⎞ ⎜⎝ ⎛ ⇒=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ⇒ == == yntymnatmaSNdTSNdMKSNτSNσKdTJTcdMIMcσ πππτπ 312243' 32⎥⎥⎥ ⎦ ⎤ ⎢⎢⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ = yntSTSMKNd π

27. ANSI / ASME Shaft Equation312243' 32sionsteady torandbendingreversedFully ⎥⎥⎥ ⎦ ⎤ ⎢⎢⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ≥ yntSTSMKNd π 31224332Static⎥⎥⎥⎦ ⎤ ⎢⎢⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≥ yySTSMNd π

28. ANSI Shaft Design Equation312243' 32sionsteady torandbendingreversedFully ⎥⎥⎥ ⎦ ⎤ ⎢⎢⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ≥ yntSTSMKNd π 1' :sionsteady tor and bending reversedFully 22=⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ +⎟⎟⎠ ⎞ ⎜⎜⎝ ⎛ ysmnaSτSσ
Can we use Soderbergor Goodman criterion?

29. Example 12-1 (p. 548)
•The system transmitting 200 hp from pinion P to gear A, and from pinion C to gear Q.
•The shaft rotating speed is 600 rpm.
•Shaft material is AISI 1144 OQT 1000

31. Example (p. 549)
•Free body diagram
•Shear and moment diagrams
•Torque at each segment
•Calculate diameter for locations A, B, C, and D (at both left and right) ABCDNo momentTorque = 21000No torque, no moment, vertical shear onlyNo torque

32. Shear and Moment DiagramsFrom bottom look upFront view

33. Design Examples

35. Design Example -Torque

37. Design Example -Forces

39. Design Examples –Shear and Moment