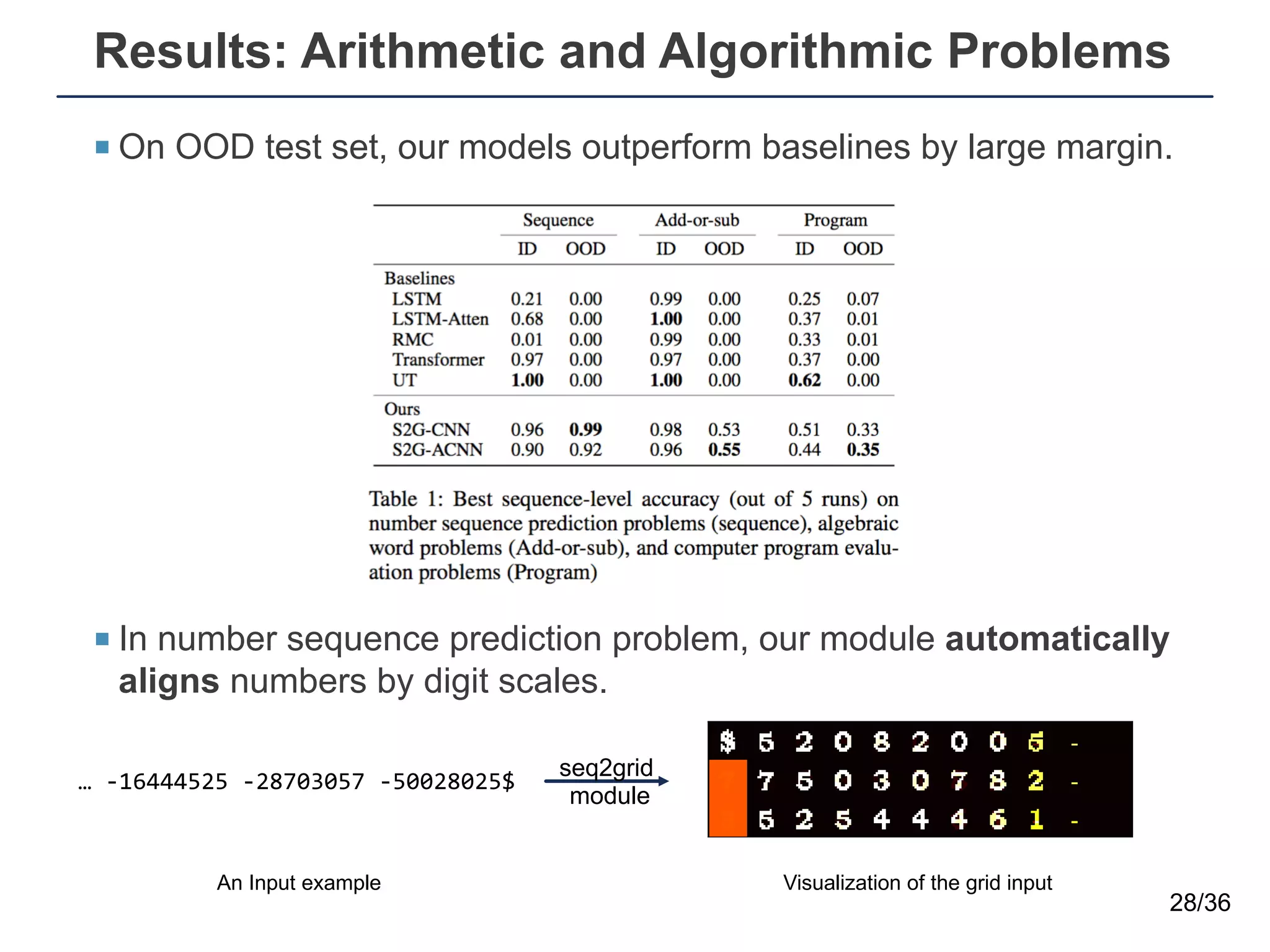
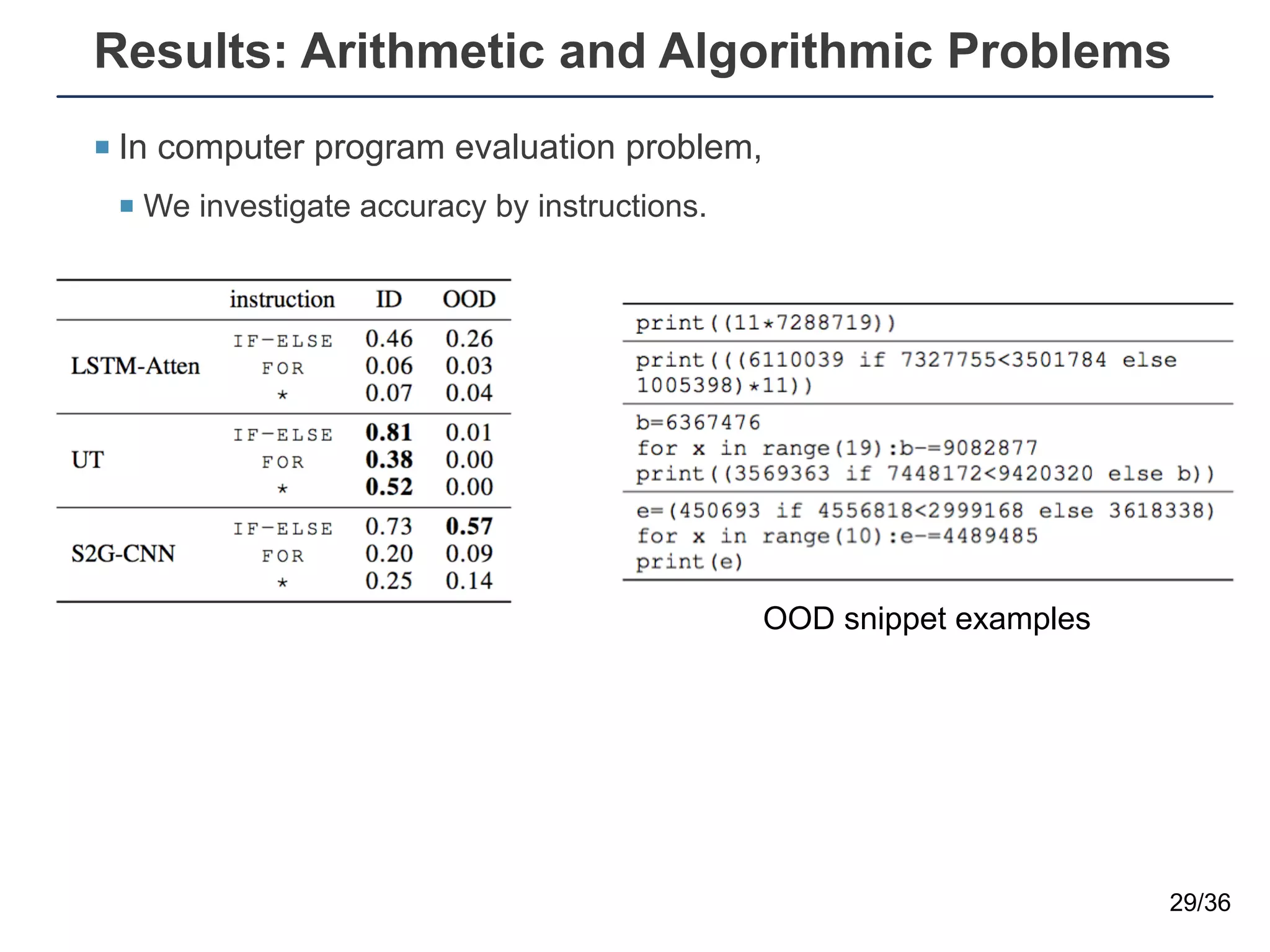
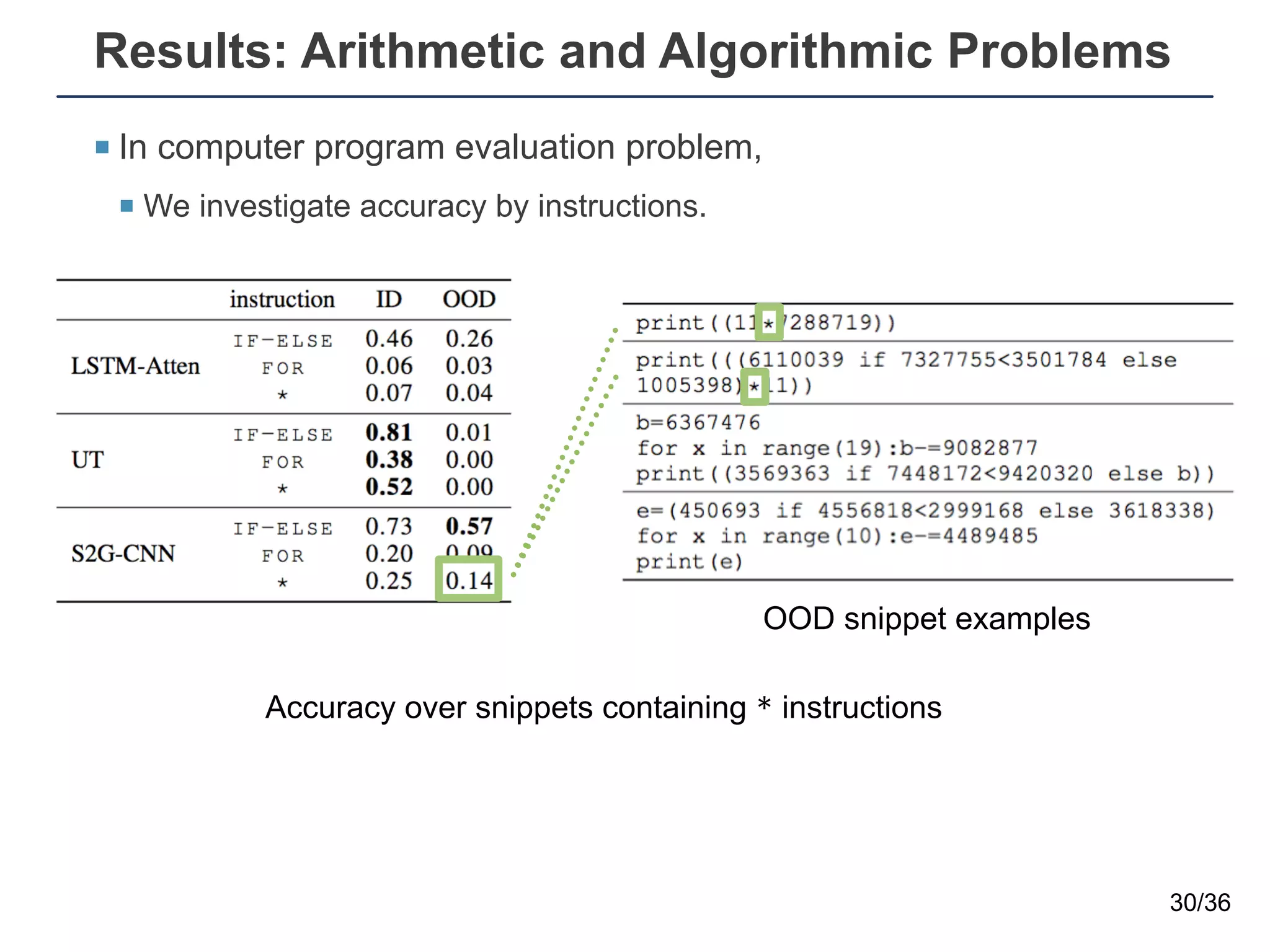
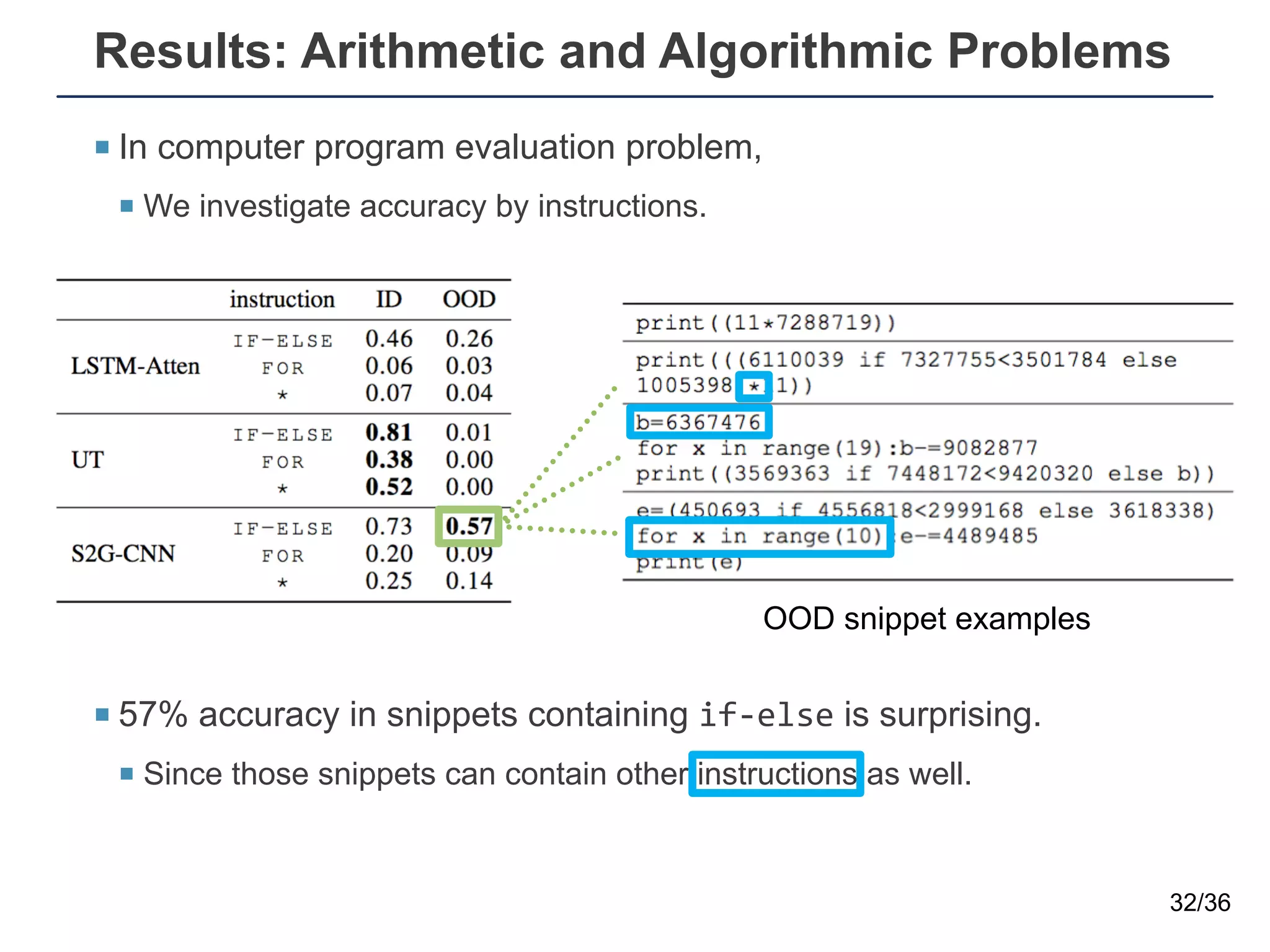
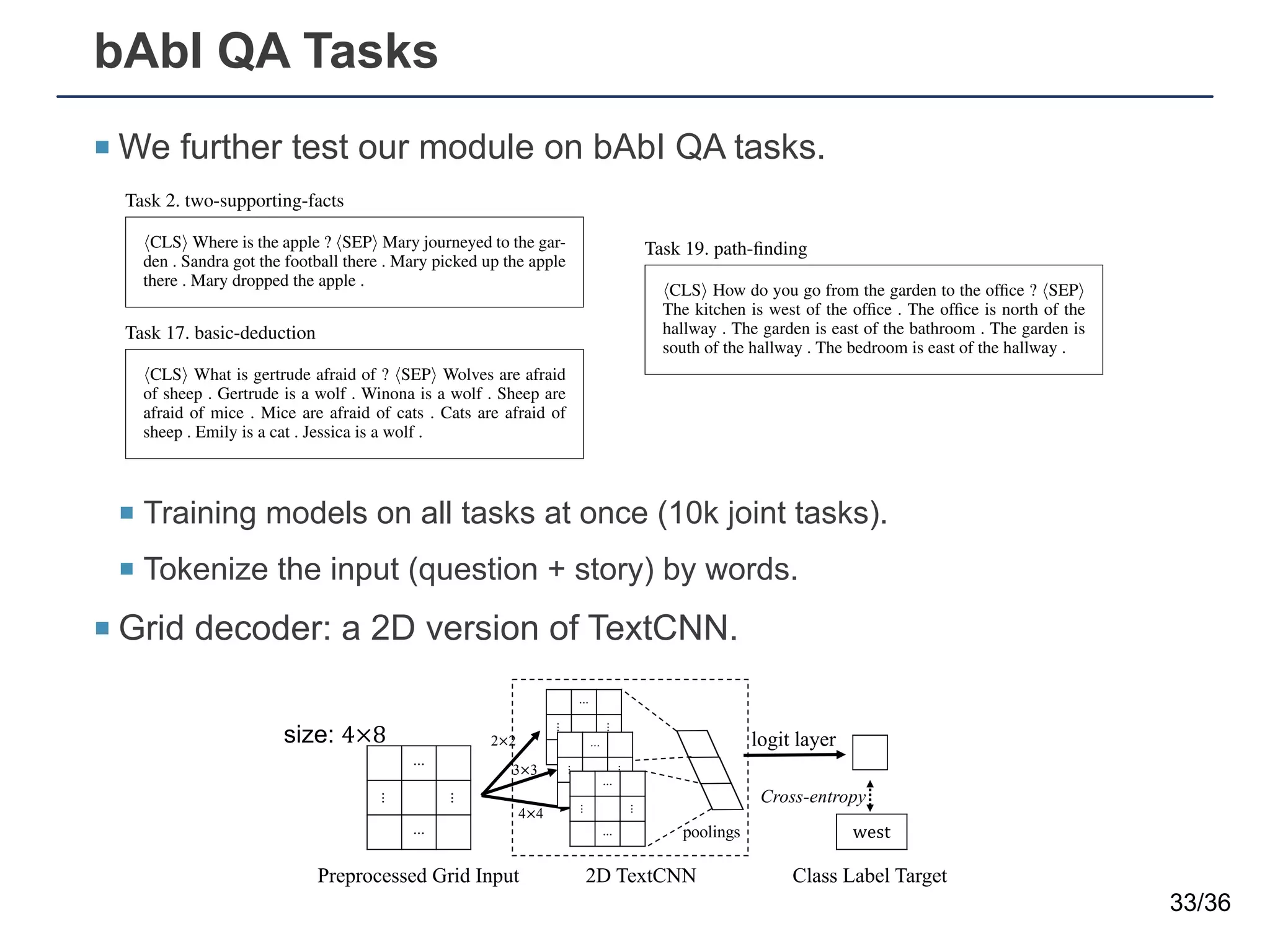
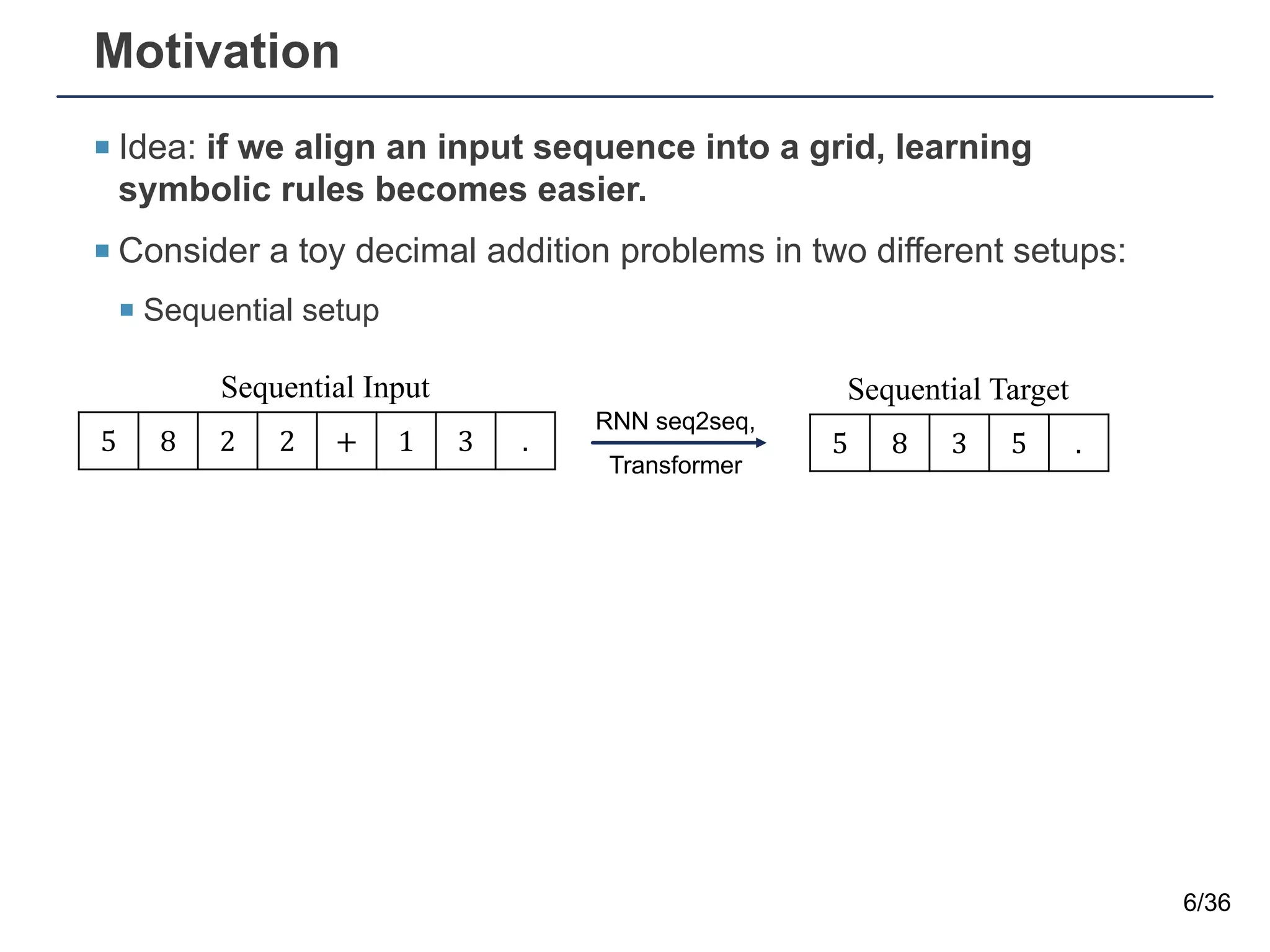
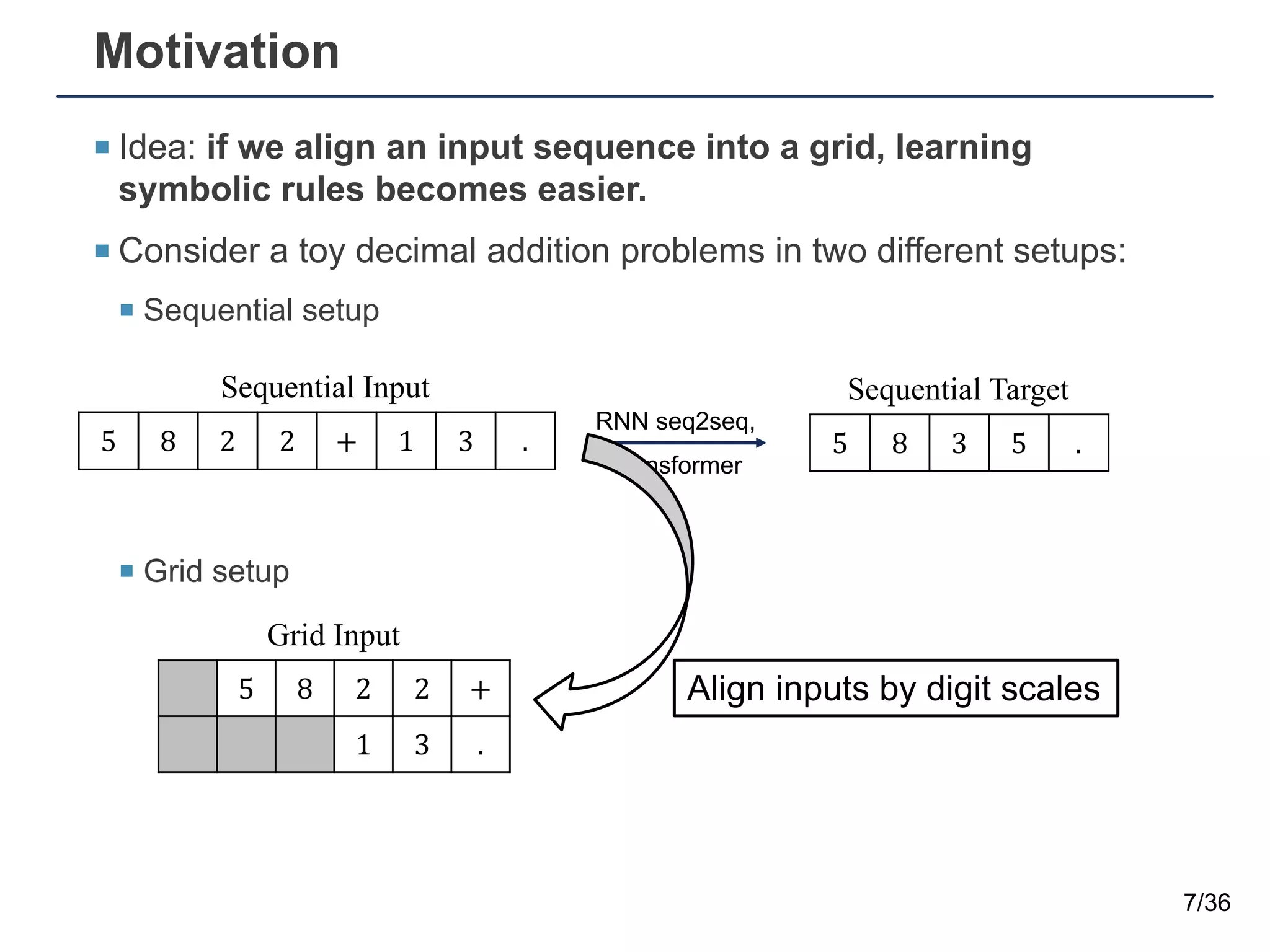
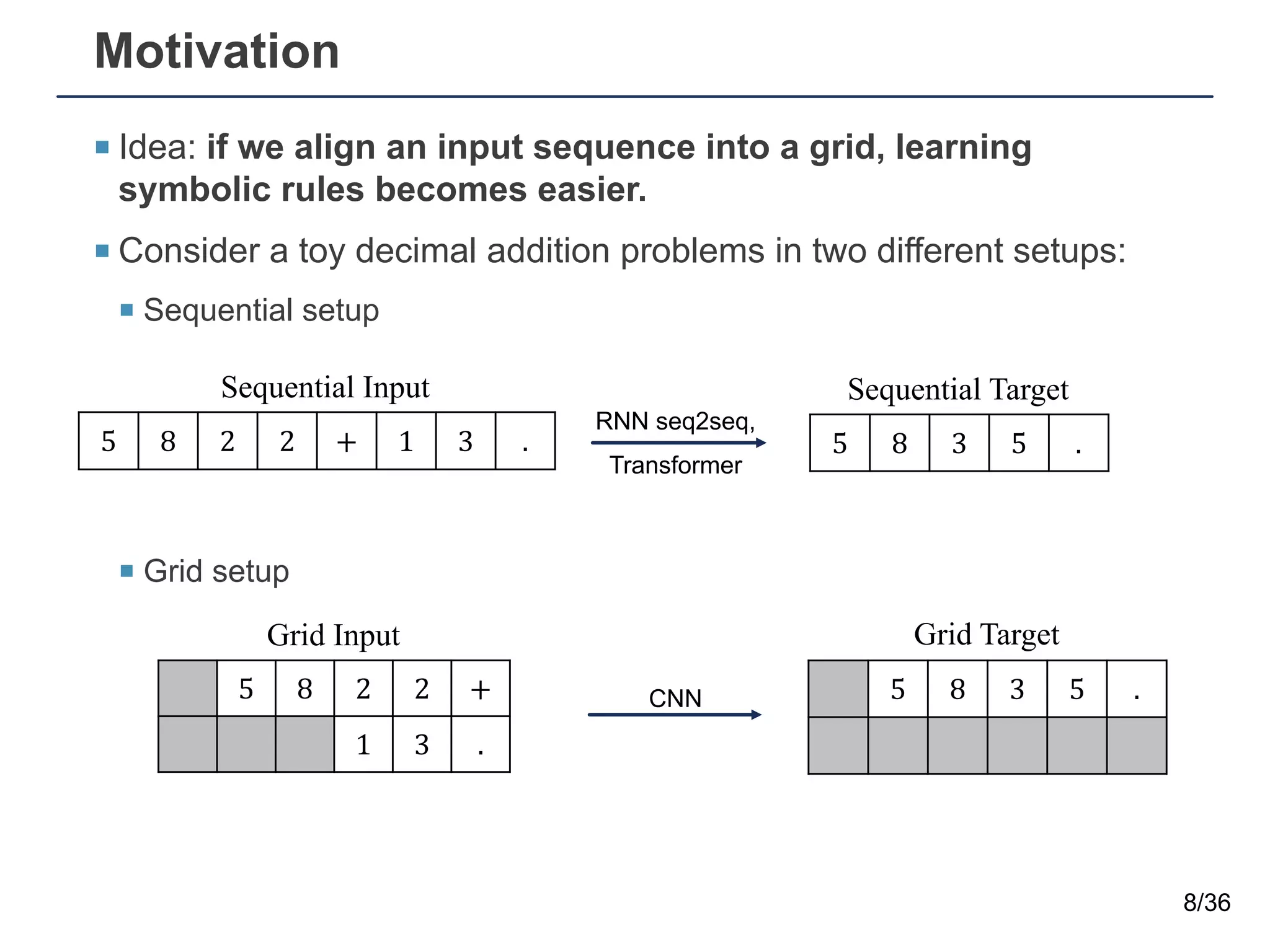
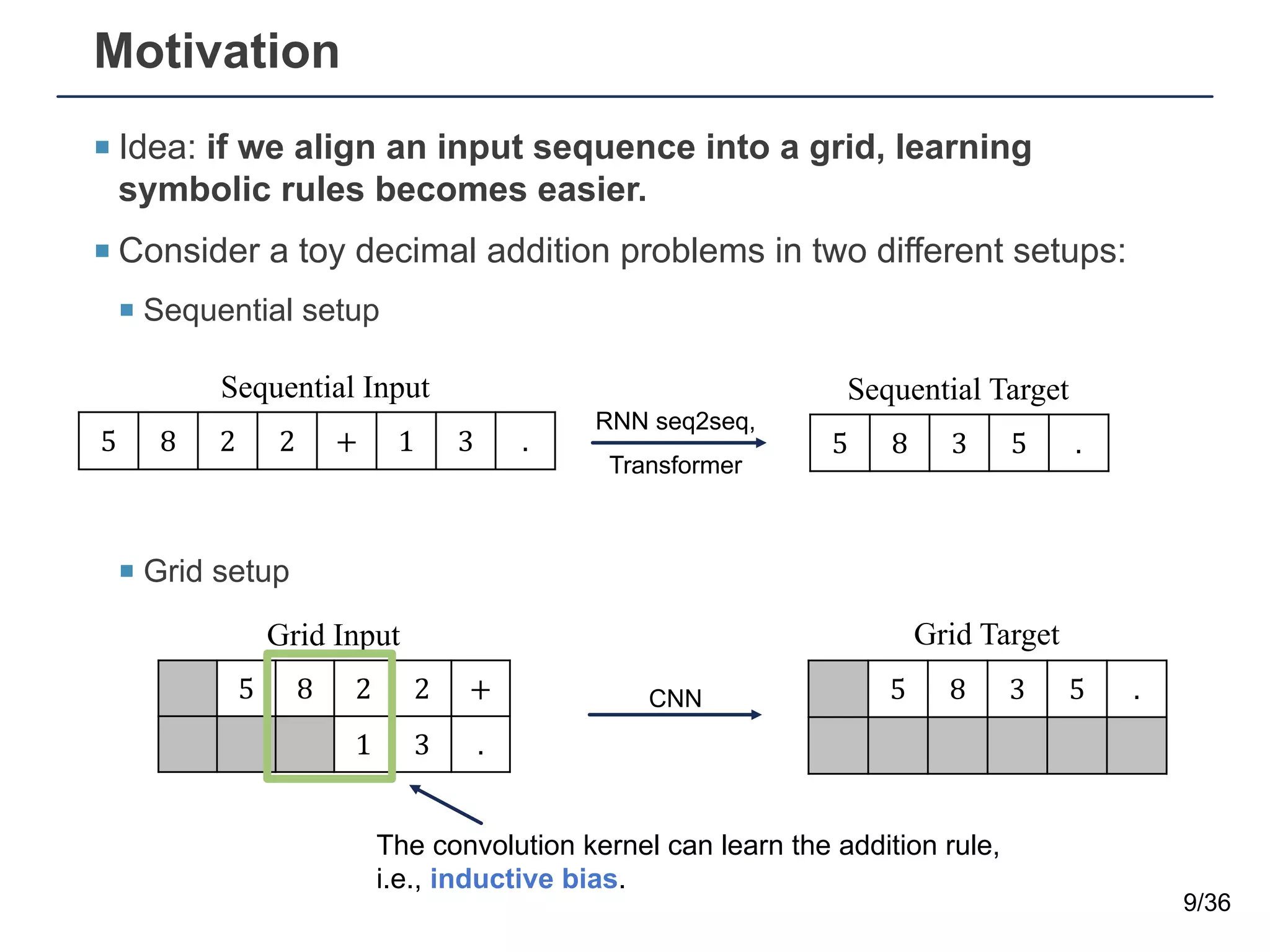
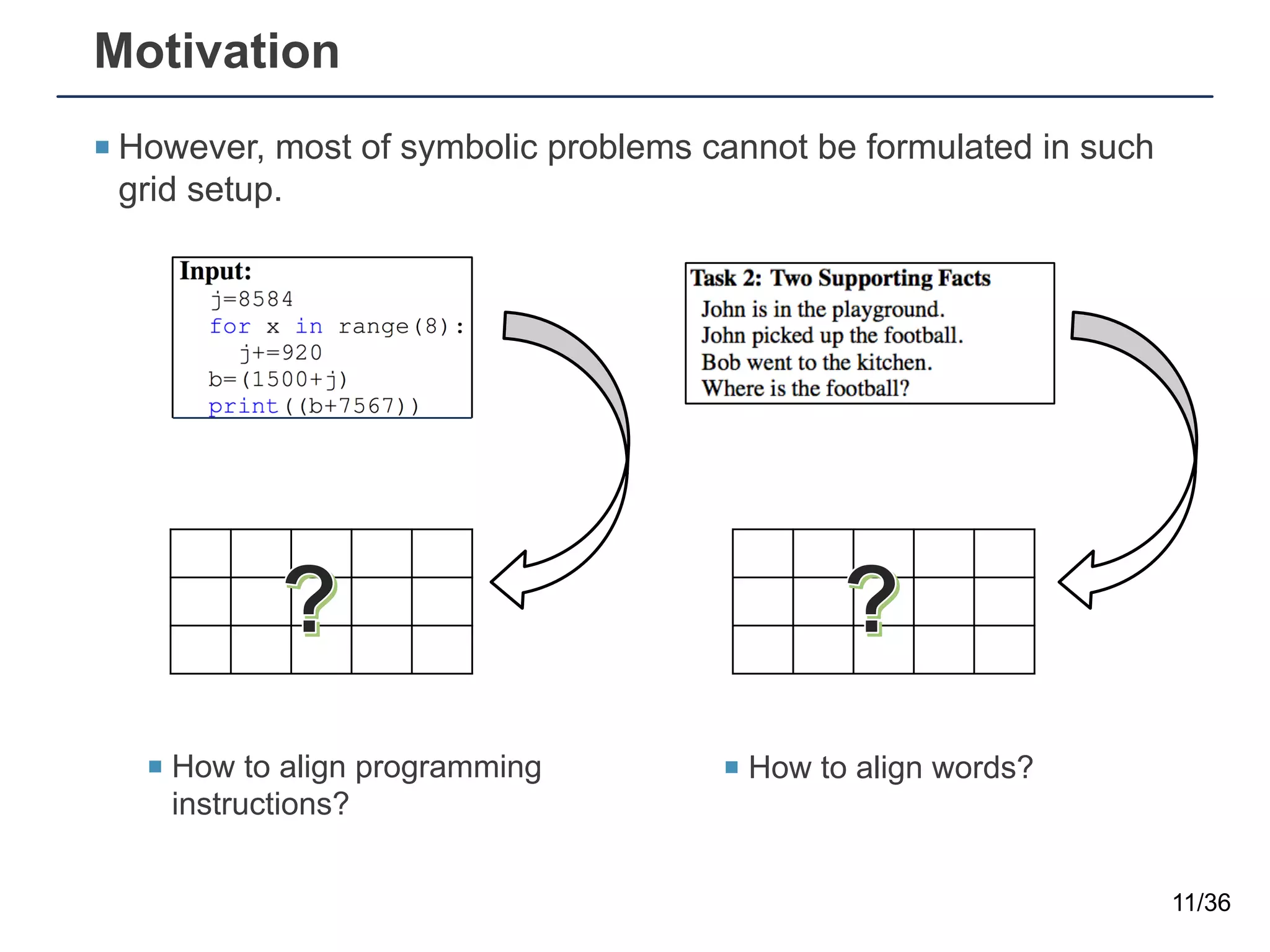
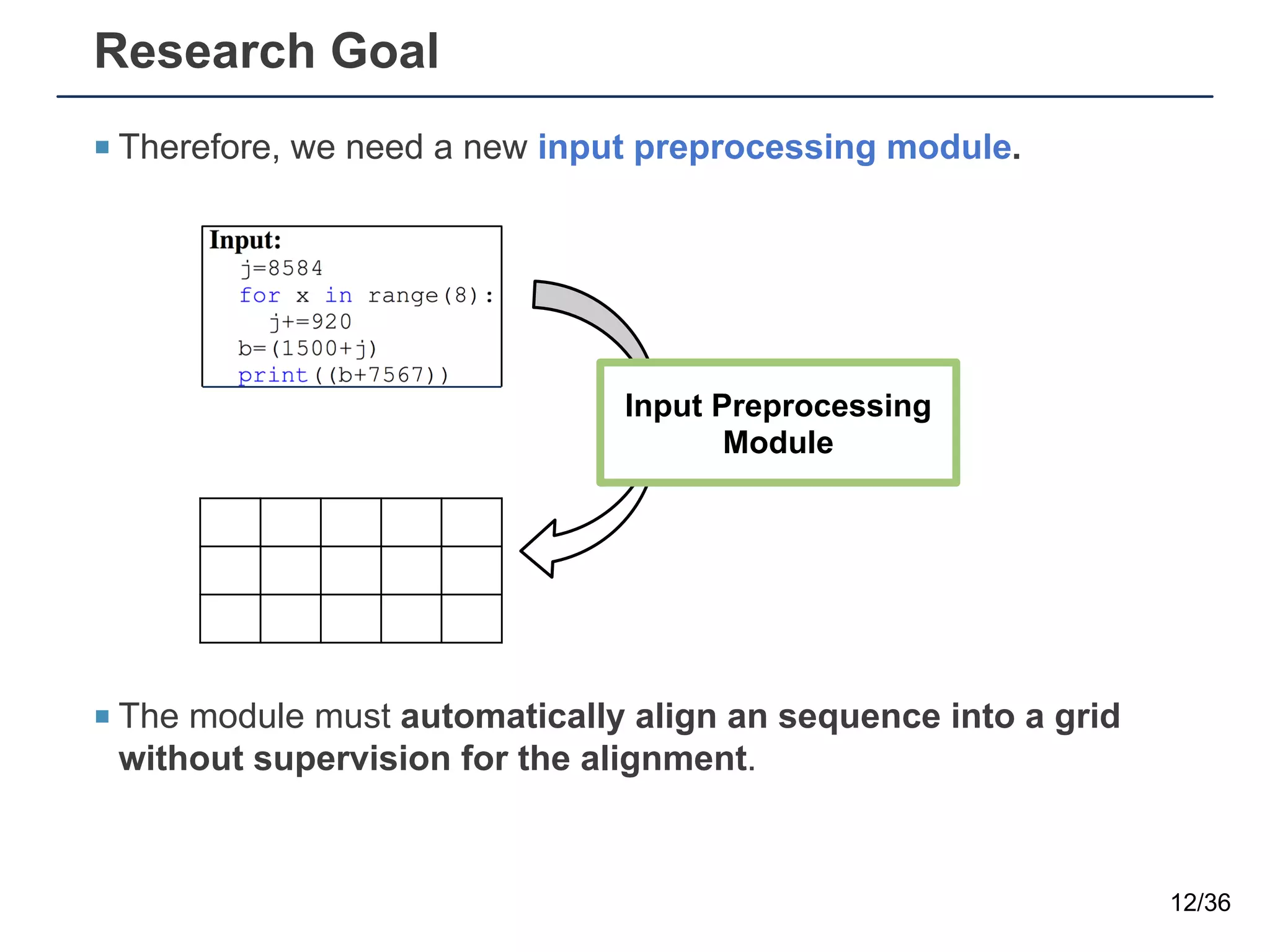
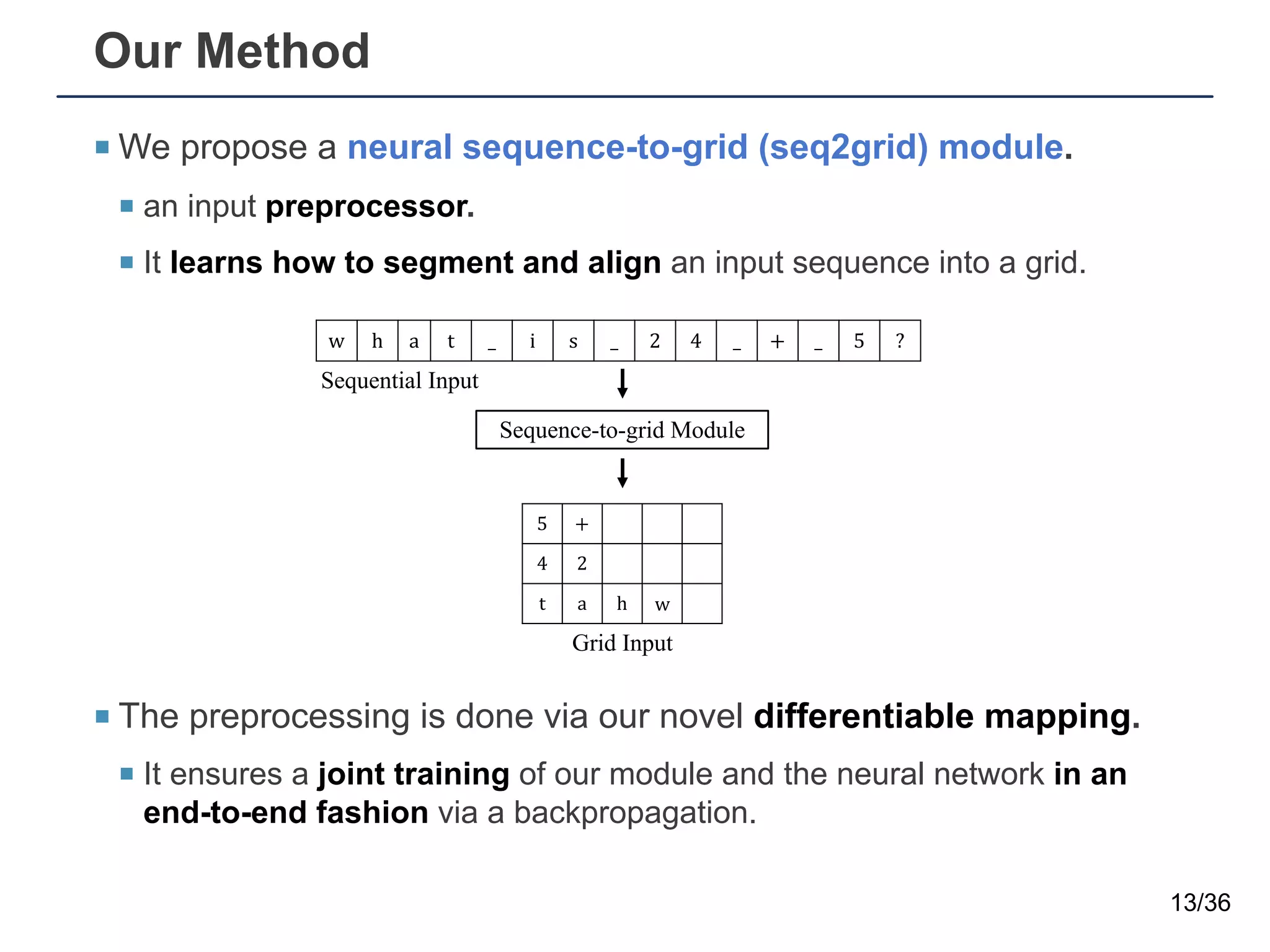
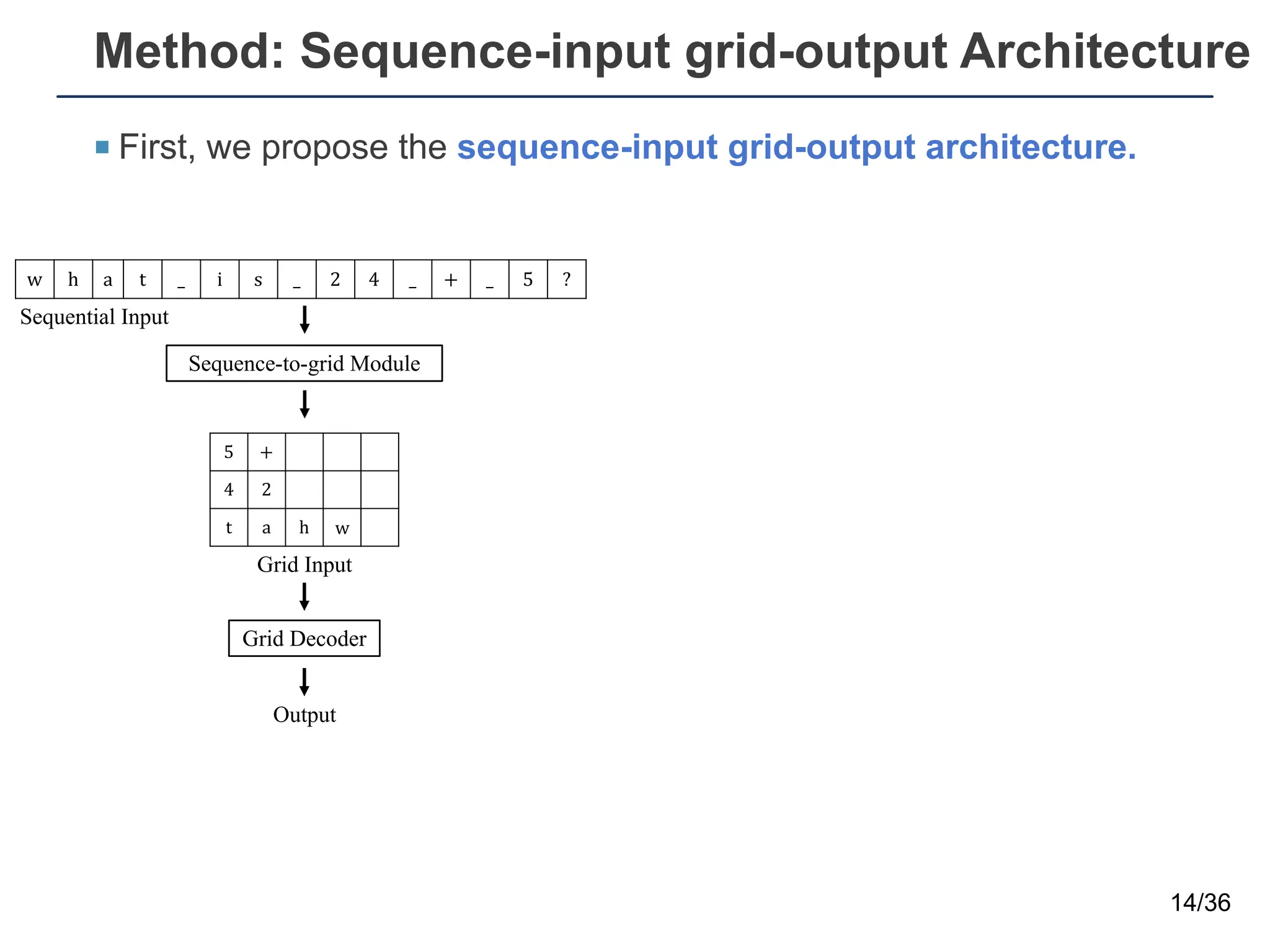
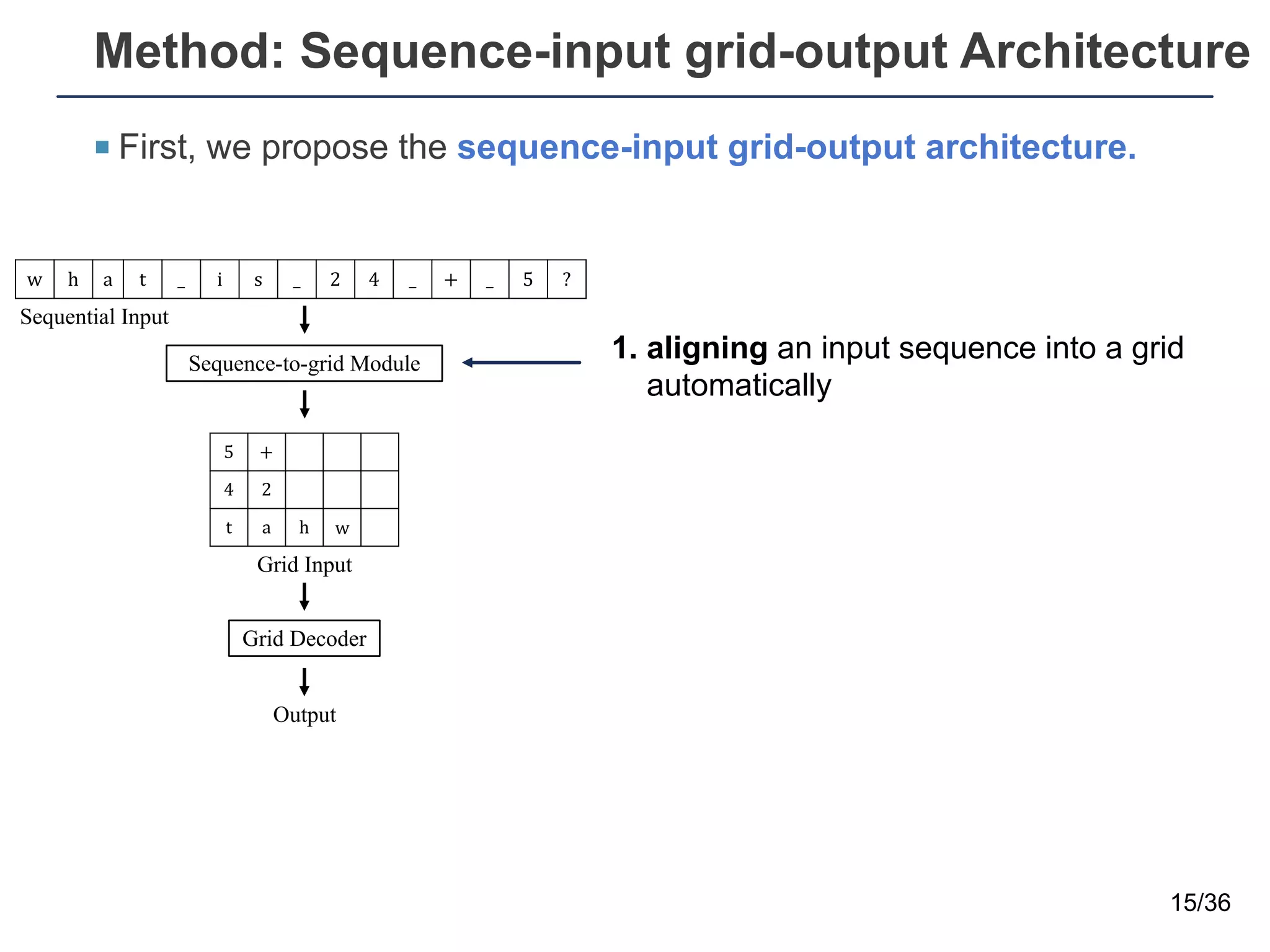
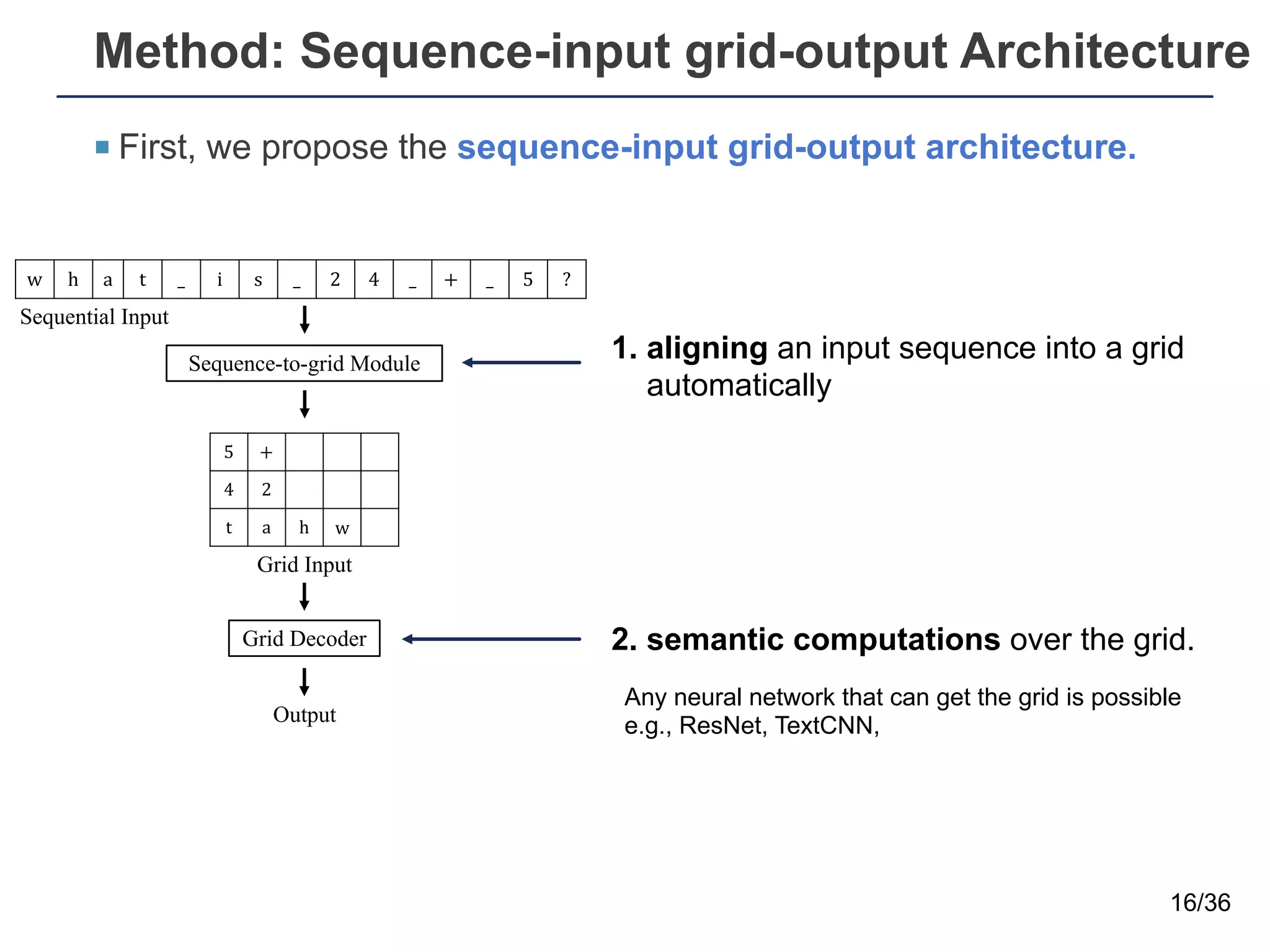
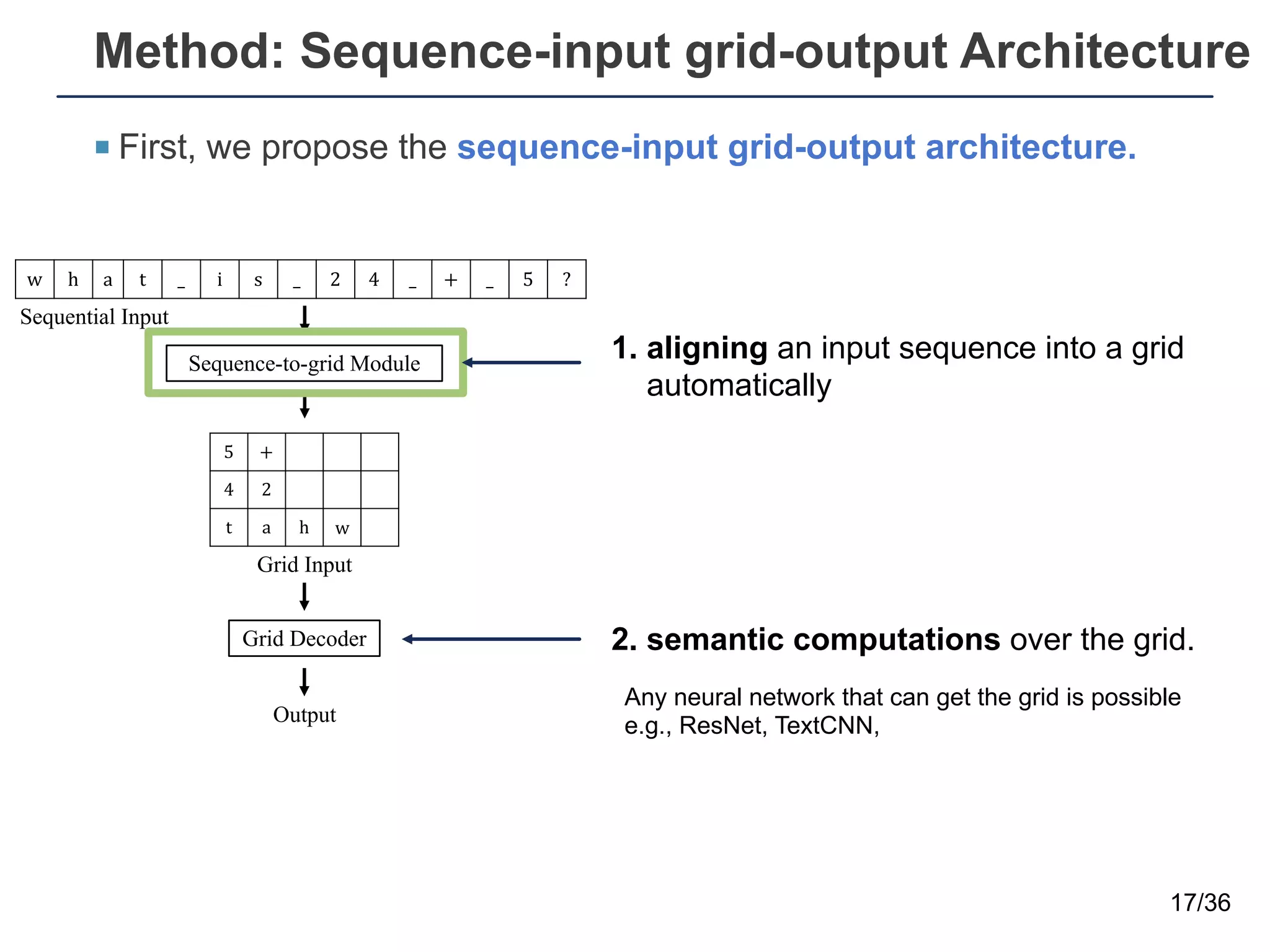
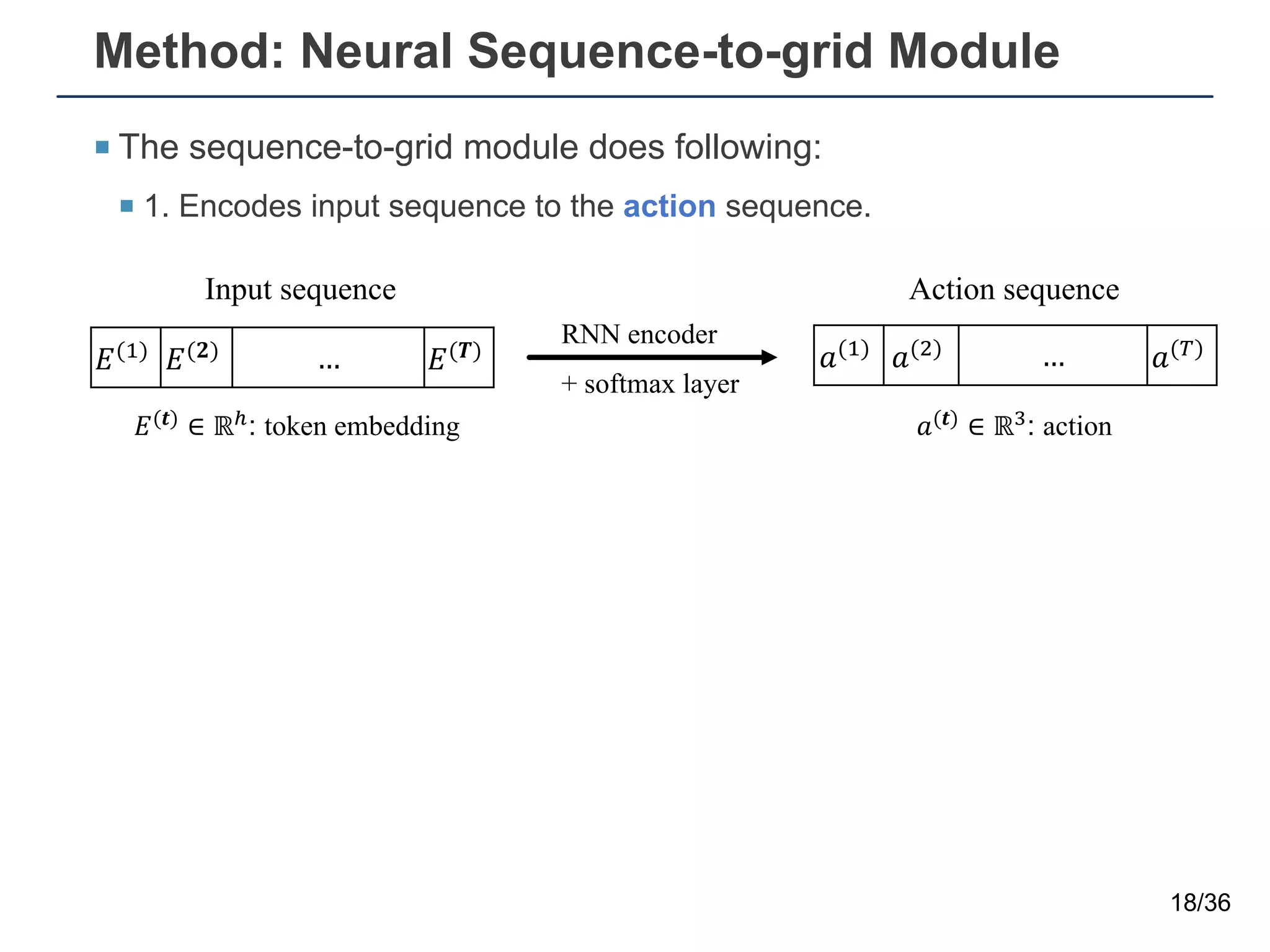
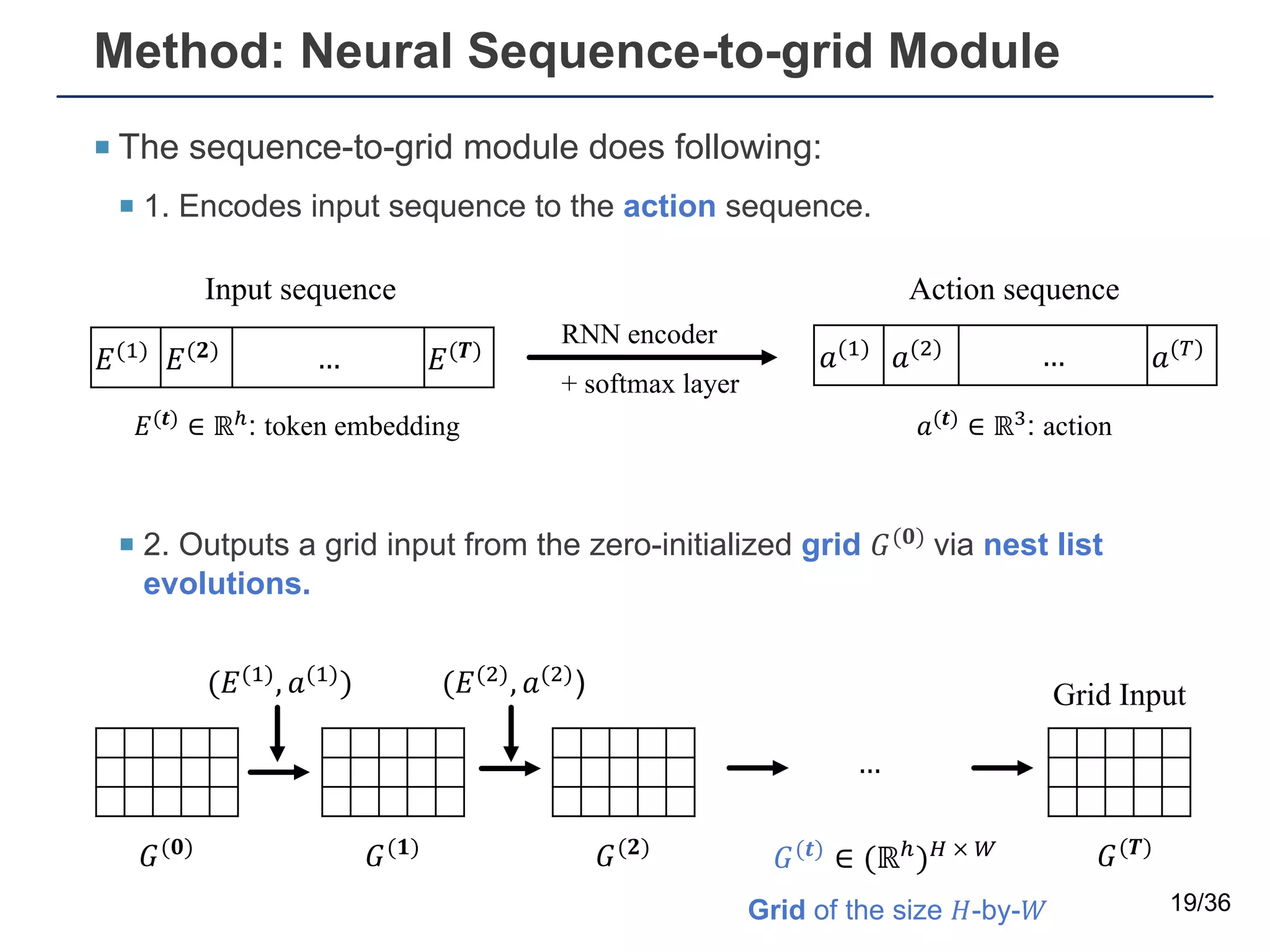
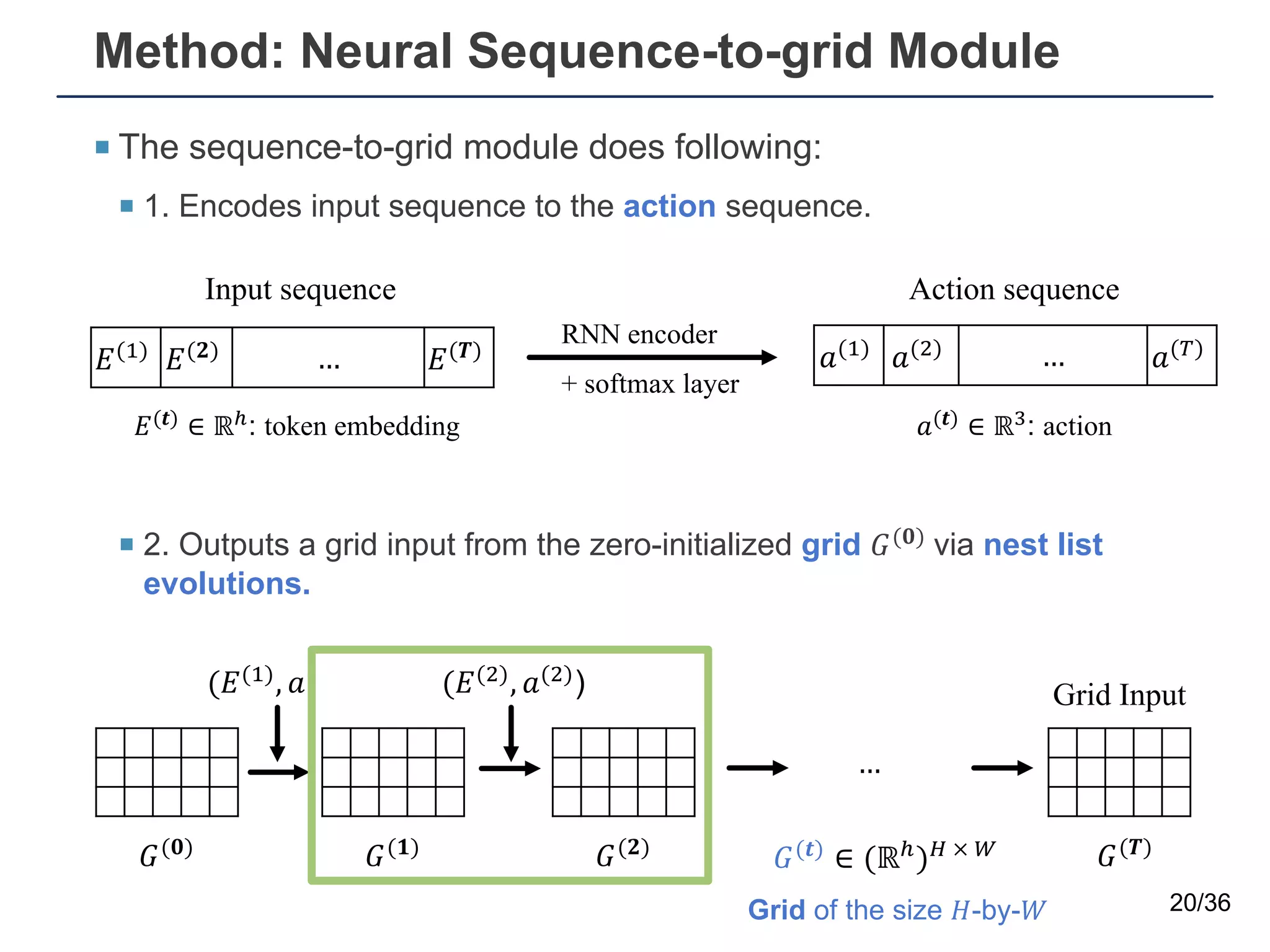
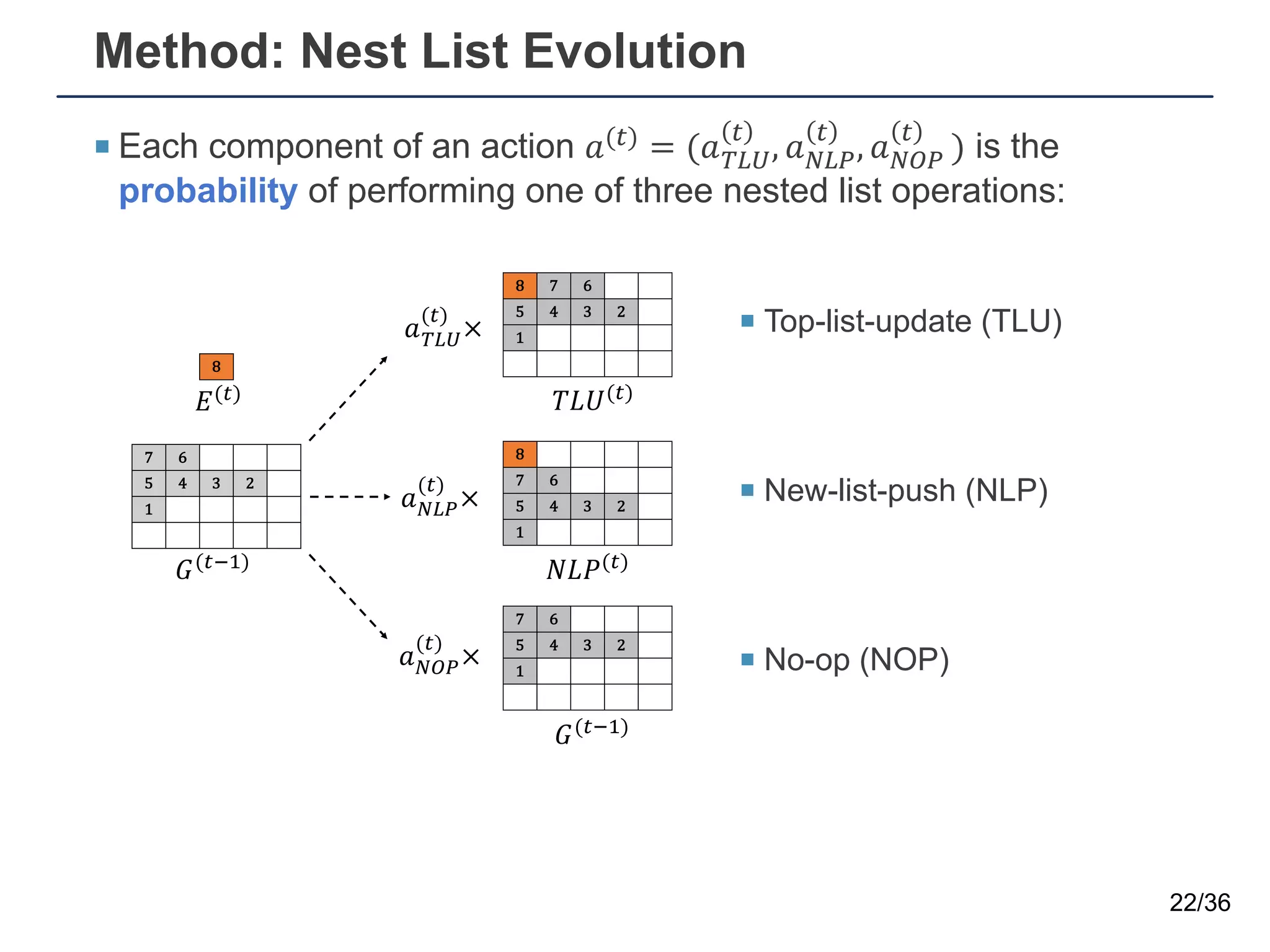
The document presents a neural sequence-to-grid (seq2grid) module designed to improve the ability of deep learning models to learn symbolic rules by aligning input sequences into grids. This method enhances the models' performance on out-of-distribution (OOD) examples, particularly in tasks like arithmetic and algorithmic problems. The seq2grid module undergoes joint training with the neural network, allowing it to effectively preprocess inputs for better generalization.

1. Neural Sequence-to-grid Module for Learning
Symbolic Rules
Segwang Kim1, Hyoungwook Nam2, Joonyoung Kim1, Kyomin Jung1
1 Seoul National University, Seoul, Korea
2 University of Illinois at Urbana-Champaign, Urbana, Illinois, USA

2. Background
¡ Symbolic reasoning problems are testbeds for assessing logical
inference abilities of deep learning models.
2/36
Program code evaluation [1] bAbI tasks [2]
[1] Zaremba, et al. Learning to execute. arXiv 2014.
[2] Weston, et al. Towards ai-complete question answering: A set of prerequisite toy tasks. ICLR 2016.

3. Background
¡ Symbolic reasoning problems are testbeds for assessing logical
inference abilities of deep learning models.
¡ The determinism of symbolic problems allows us to systematically
test deep learning models with out-of-distribution (OOD) data.
¡ Humans with algebraic mind can naturally extend learned rules.
3/36
5 8 2 + 1 = 3 0 5 3 4 + 4 2 1 =
[1] Zaremba, et al. Learning to execute. arXiv 2014.
[2] Weston, et al. Towards ai-complete question answering: A set of prerequisite toy tasks. ICLR 2016.
Program code evaluation [1] bAbI tasks [2]
6 7 + 3 = 6 9 5 2 1 + 5 0 0 2 9 =
Training examples OOD Test Examples

4. Background
¡ However, deep learning models cannot extend learned rules to
OOD (out-of-distribution) examples.
4/36
[3] Nam, et al. Number sequence prediction problems and computational power of neural networks, AAAI 2019
[4] Saxton, et al. Analysing Mathmatical Reasoning Abilities of Neural Models, ICLR 2019.
Number sequence prediction problems [3]
Middle school level mathematics problems [4]
Error
Accuracy

5. Motivation
¡ Idea: if we align an input sequence into a grid, learning
symbolic rules becomes easier.
5/36

6. Motivation
¡ Idea: if we align an input sequence into a grid, learning
symbolic rules becomes easier.
¡ Consider a toy decimal addition problems in two different setups:
¡ Sequential setup
6/36
5 8 2 2 + 1 3 . 5 8 3 5 .
Sequential Input Sequential Target
RNN seq2seq,
Transformer

7. Motivation
¡ Idea: if we align an input sequence into a grid, learning
symbolic rules becomes easier.
¡ Consider a toy decimal addition problems in two different setups:
¡ Sequential setup
¡ Grid setup
7/36
5 8 2 2 +
1 3 .
5 8 2 2 + 1 3 . 5 8 3 5 .
Sequential Input Sequential Target
Grid Input
RNN seq2seq,
Transformer
Align inputs by digit scales

8. Motivation
¡ Idea: if we align an input sequence into a grid, learning
symbolic rules becomes easier.
¡ Consider a toy decimal addition problems in two different setups:
¡ Sequential setup
¡ Grid setup
8/36
5 8 2 2 +
1 3 .
5 8 2 2 + 1 3 . 5 8 3 5 .
5 8 3 5 .
Sequential Input Sequential Target
Grid Target
Grid Input
RNN seq2seq,
Transformer
CNN

9. Motivation
¡ Idea: if we align an input sequence into a grid, learning
symbolic rules becomes easier.
¡ Consider a toy decimal addition problems in two different setups:
¡ Sequential setup
¡ Grid setup
9/36
5 8 2 2 +
1 3 .
5 8 2 2 + 1 3 . 5 8 3 5 .
5 8 3 5 .
Sequential Input Sequential Target
Grid Target
Grid Input
The convolution kernel can learn the addition rule,
i.e., inductive bias.
RNN seq2seq,
Transformer
CNN

10. ____________________________
Sequential
Setup
Grid
Setup
Usefulness of Aligned Grid Inputs
¡ Depending on setups, OOD generalization is achieved or not.
¡ Providing aligned grid inputs for CNN can be key to extend
symbolic rules.
10/36

11. Motivation
¡ However, most of symbolic problems cannot be formulated in such
grid setup.
11/36
¡ How to align programming
instructions?
¡ How to align words?

12. Research Goal
¡ Therefore, we need a new input preprocessing module.
¡ The module must automatically align an sequence into a grid
without supervision for the alignment.
12/36
Input Preprocessing
Module

13. Our Method
¡ We propose a neural sequence-to-grid (seq2grid) module.
¡ an input preprocessor.
¡ It learns how to segment and align an input sequence into a grid.
¡ The preprocessing is done via our novel differentiable mapping.
¡ It ensures a joint training of our module and the neural network in an
end-to-end fashion via a backpropagation.
13/36
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output

14. Method: Sequence-input grid-output Architecture
¡ First, we propose the sequence-input grid-output architecture.
14/36
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output

15. Method: Sequence-input grid-output Architecture
¡ First, we propose the sequence-input grid-output architecture.
15/36
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output
1. aligning an input sequence into a grid
automatically

16. Method: Sequence-input grid-output Architecture
¡ First, we propose the sequence-input grid-output architecture.
16/36
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output
2. semantic computations over the grid.
Any neural network that can get the grid is possible
e.g., ResNet, TextCNN,
1. aligning an input sequence into a grid
automatically

17. Method: Sequence-input grid-output Architecture
¡ First, we propose the sequence-input grid-output architecture.
17/36
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output
Any neural network that can get the grid is possible
e.g., ResNet, TextCNN,
2. semantic computations over the grid.
1. aligning an input sequence into a grid
automatically

18. ¡ The sequence-to-grid module does following:
¡ 1. Encodes input sequence to the action sequence.
Method: Neural Sequence-to-grid Module
18/36
Input sequence
!(#)
!(%) … !(') ((#)
(()) … ((*)
Action sequence
!(+) ∈ ℝ.: token embedding ((+) ∈ ℝ/: action
RNN encoder
+ softmax layer

19. ¡ The sequence-to-grid module does following:
¡ 1. Encodes input sequence to the action sequence.
¡ 2. Outputs a grid input from the zero-initialized grid !(#) via nest list
evolutions.
Method: Neural Sequence-to-grid Module
19/36
Input sequence
%(&)
%(') … %())
Grid Input
*(&)
*(+) … *(,)
Action sequence
%(-) ∈ ℝ0: token embedding *(-) ∈ ℝ1: action
RNN encoder
+ softmax layer
!(#)
!(-)
∈ (ℝ0
)2 × 4
!(5)
!(')
!())
…
(%(&), *(&)) (%(+), *(+))
Grid of the size 7-by-8

20. ¡ The sequence-to-grid module does following:
¡ 1. Encodes input sequence to the action sequence.
¡ 2. Outputs a grid input from the zero-initialized grid !(#) via nest list
evolutions.
Method: Neural Sequence-to-grid Module
20/36
Input sequence
%(&)
%(') … %())
Grid Input
*(&)
*(+) … *(,)
Action sequence
%(-) ∈ ℝ0: token embedding *(-) ∈ ℝ1: action
RNN encoder
+ softmax layer
!(#)
!(-)
∈ (ℝ0
)2 × 4
!(5)
!(')
!())
…
(%(&), *(&)) (%(+), *(+))
Grid of the size 7-by-8

21. Method: Nest List Evolution
21/36
7 6
5 4 3 2
1
8
7 6
5 4 3 2
1
8 7 6
5 4 3 2
1
8
7 6
5 4 3 2
1
)*+,
(.)
×
)1+2
(.)
×
)132
(.)
×
4(.)
5(.67)
89:(.)
;9<(.)
5(.67)
= 5(.)
+
¡ Top-list-update (TLU)
¡ New-list-push (NLP)
¡ No-op (NOP)
nested list operations
Candidates

22. ¡ Each component of an action !(#) = (!&'(
#
, !*'+
#
, !*,+
#
) is the
probability of performing one of three nested list operations:
Method: Nest List Evolution
22/36
7 6
5 4 3 2
1
8
7 6
5 4 3 2
1
8 7 6
5 4 3 2
1
8
7 6
5 4 3 2
1
)*+,
(.)
×
)1+2
(.)
×
)132
(.)
×
4(.)
5(.67)
89:(.)
;9<(.)
5(.67)
= 5(.)
+
¡ Top-list-update (TLU)
¡ New-list-push (NLP)
¡ No-op (NOP)

23. ¡ Each component of an action !(#) = (!&'(
#
, !*'+
#
, !*,+
#
) is the
probability of performing one of three nested list operations:
¡ In each evolution step, -(#./) with 0 # , ! # grows to -(#)
Method: Nest List Evolution
23/36
7 6
5 4 3 2
1
8
7 6
5 4 3 2
1
8 7 6
5 4 3 2
1
8
7 6
5 4 3 2
1
)*+,
(.)
×
)1+2
(.)
×
)132
(.)
×
4(.)
5(.67)
89:(.)
;9<(.)
5(.67)
= 5(.)
+
-(#)
= !&'(
#
⋅ 234 #
+ !*'+
#
⋅ 234 #
+ !*,+
#
⋅ - #./
¡ Top-list-update (TLU)
¡ New-list-push (NLP)
¡ No-op (NOP)

24. Arithmetic and Algorithmic Problems
¡ We test our module on three arithmetic and algorithmic problems.
¡ 1M training examples.
¡ Tokenize all examples by characters and decimal digits.
24/36
Number sequence prediction problem
Computer program evaluation problem
Algebraic word problem
Input
Target
7008 -205 4 7221.
14233.
Input
Target
j=891
for x in range(11):j-=878
print((368 if 821<874 else j)).
368.
Input
Target
Sum -3240245475 and 11.
368.
Number sequence prediction problem
Computer program evaluation problem
Algebraic word problem
Input
Target
7008 -205 4 7221.
14233.
Input
Target
j=891
for x in range(11):j-=878
print((368 if 821<874 else j)).
368.
Input
Target
Sum -3240245475 and 11.
368.
Number sequence prediction problem
Computer program evaluation problem
Algebraic word problem
Input
Target
7008 -205 4 7221.
14233.
Input
Target
j=891
for x in range(11):j-=878
print((368 if 821<874 else j)).
368.
Input
Target
Sum -3240245475 and 11.
368.

25. Arithmetic and Algorithmic Problems
¡ We test our module on three arithmetic and algorithmic problems.
¡ 1M training examples.
¡ Tokenize all examples by characters and decimal digits.
¡ Two test sets (10k test examples each).
¡ In-distribution (ID): examples sampled from the training distribution.
¡ Out-of-distribution (OOD): examples with unprecedented longer digits.
25/36
Number sequence prediction problem
Computer program evaluation problem
Algebraic word problem
Input
Target
7008 -205 4 7221.
14233.
Input
Target
j=891
for x in range(11):j-=878
print((368 if 821<874 else j)).
368.
Input
Target
Sum -3240245475 and 11.
368.
Number sequence prediction problem
Computer program evaluation problem
Algebraic word problem
Input
Target
7008 -205 4 7221.
14233.
Input
Target
j=891
for x in range(11):j-=878
print((368 if 821<874 else j)).
368.
Input
Target
Sum -3240245475 and 11.
368.
Number sequence prediction problem
Computer program evaluation problem
Algebraic word problem
Input
Target
7008 -205 4 7221.
14233.
Input
Target
j=891
for x in range(11):j-=878
print((368 if 821<874 else j)).
368.
Input
Target
Sum -3240245475 and 11.
368.

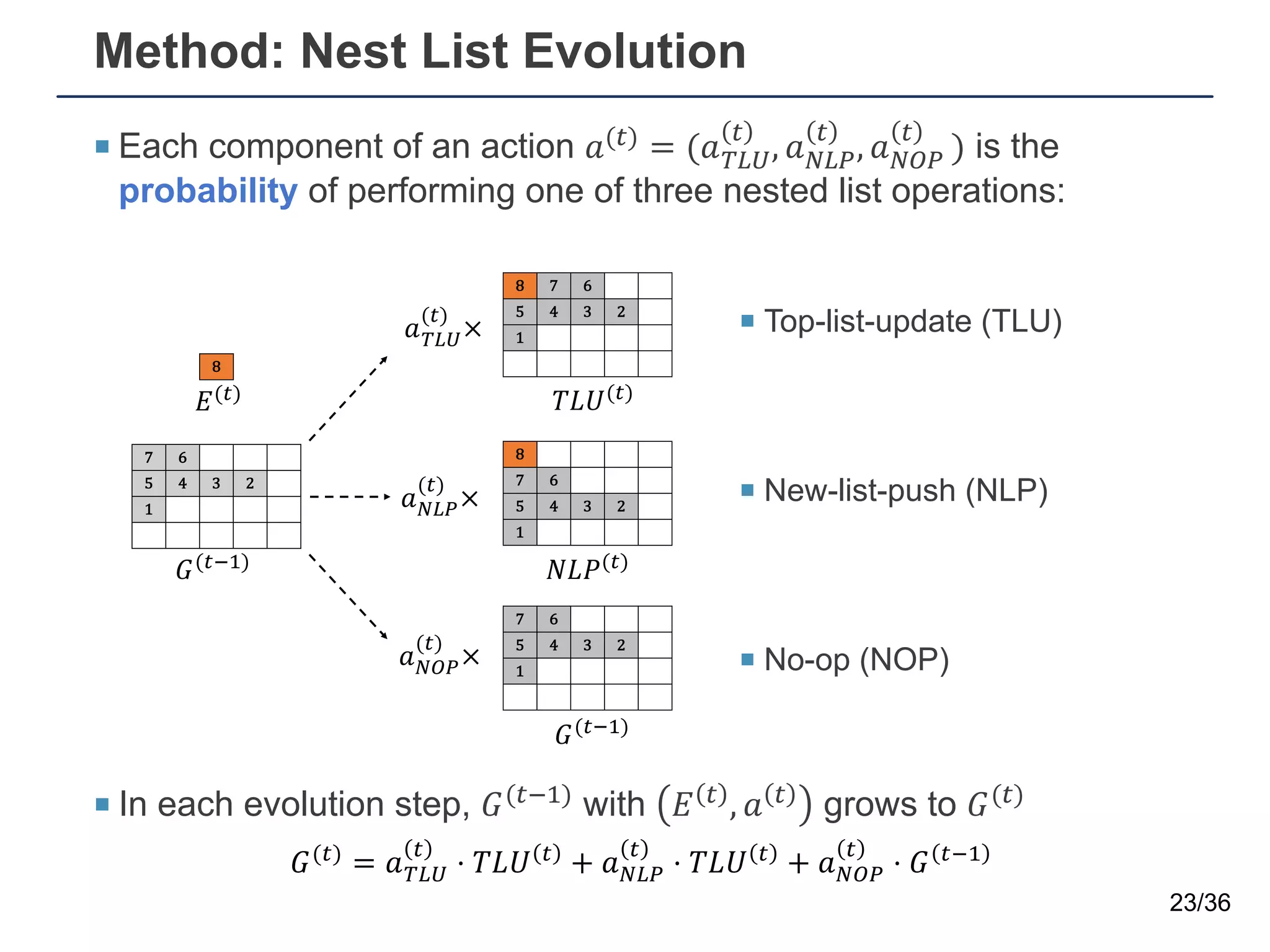
26. Arithmetic and Algorithmic Problems
¡ Grid decoder: three stacks of 3-layered bottleneck blocks of ResNet.
26/36
[5] He, et al. Deep Residual Learning for Image Recognition, CVPR 2015
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output
3-layered bottleneck blocks [5]
×3
size: 3×25

27. Arithmetic and Algorithmic Problems
¡ Grid decoder: three stacks of 3-layered bottleneck blocks of ResNet.
¡ The seq2grid module and the grid decoder are simultaneously
trained by reducing cross-entropy loss.
27/36
[5] He, et al. Deep Residual Learning for Image Recognition, CVPR 2015
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output
Sequence-to-grid Module
Sequential Input
w h a t _ i s _ 2 4 _ + _ 5 ?
5 +
4 2
t a h w
Grid Input
Grid Decoder
Output
3-layered bottleneck blocks [5]
×3
bottleneck
blocks
9 2 ∅
Flipped Sequential Target
Cross-entropy
logit layer
Preprocessed Grid Input
2 9
Original Target
size: 3×25
pad token

28. Results: Arithmetic and Algorithmic Problems
¡ On OOD test set, our models outperform baselines by large margin.
¡ In number sequence prediction problem, our module automatically
aligns numbers by digit scales.
28/36
… -16444525 -28703057 -50028025$
An Input example Visualization of the grid input
seq2grid
module

29. Results: Arithmetic and Algorithmic Problems
¡ In computer program evaluation problem,
¡ We investigate accuracy by instructions.
29/36
OOD snippet examples

30. Results: Arithmetic and Algorithmic Problems
¡ In computer program evaluation problem,
¡ We investigate accuracy by instructions.
30/36
Accuracy over snippets containing * instructions
OOD snippet examples

31. Results: Arithmetic and Algorithmic Problems
31/36
¡ In computer program evaluation problem,
¡ We investigate accuracy by instructions.
¡ 57% accuracy in snippets containing if-else is surprising.
OOD snippet examples

32. Results: Arithmetic and Algorithmic Problems
¡ In computer program evaluation problem,
¡ We investigate accuracy by instructions.
¡ 57% accuracy in snippets containing if-else is surprising.
¡ Since those snippets can contain other instructions as well.
32/36
OOD snippet examples

33. bAbI QA Tasks
¡ We further test our module on bAbI QA tasks.
¡ Training models on all tasks at once (10k joint tasks).
¡ Tokenize the input (question + story) by words.
¡ Grid decoder: a 2D version of TextCNN.
33/36
LSTM-Atten F O R 0.06 0.03
* 0.07 0.04
UT
I F-E L S E 0.81 0.01
F O R 0.38 0.00
* 0.52 0.00
S2G-ACNN
I F-E L S E 0.80 0.69
F O R 0.14 0.12
* 0.28 0.15
Table 2: Accuracy by instruction types of the best runs on the
computer program evaluation problems. Each test set is split
into three by the instructions used (for, multiply, if-else).
print((11*9223698))
print((12*(6707143 if 2025491>9853525 else
6816666)))
b=8582286
for x in range(20):b-=8256733
print(b)
d=(1017291 if 7117986>9036040 else 5725637)
for x in range(2):d-=6827279
print(d)
Figure 7: Some OOD code snippet examples correctly pre-
dicted by the best run of the S2G-ACNN. Note that FOR or
* instruction requiring non-linear time complexity.
ID test set. This shows that extending learned rules to longer
numbers is extremely difficult via sequential processing.
As for the number sequence prediction problems, their
OOD test results serve as unit tests for the seq2grid module
since it needs to align digit symbols on the grid according
to their scales. Indeed, Figure 6a shows that our module au-
tomatically finds such alignments which are similar to the
manually designed grid of digits as shown in Figure 1.
As for the algebraic word problems, they require context-
dependent arithmetic unlike the fixed progression rules in
number sequence prediction problems. In particular, linguis-
hCLSi Where is the apple ? hSEPi Mary journeyed to the gar-
den . Sandra got the football there . Mary picked up the apple
there . Mary dropped the apple .
Task 17. basic-deduction
hCLSi What is gertrude afraid of ? hSEPi Wolves are afraid
of sheep . Gertrude is a wolf . Winona is a wolf . Sheep are
afraid of mice . Mice are afraid of cats . Cats are afraid of
sheep . Emily is a cat . Jessica is a wolf .
Task 19. path-finding
hCLSi How do you go from the garden to the office ? hSEPi
The kitchen is west of the office . The office is north of the
hallway . The garden is east of the bathroom . The garden is
south of the hallway . The bedroom is east of the hallway .
Figure 8: Input examples of the bAbI QA tasks.
structions, our S2G-ACNN achieves almost 70% accuracy,
implying that it does not randomly pick one branch between
two possible branches. For the non-linear operations, the
S2G-ACNN shows little understanding compared with the
UT on the ID test set. However, the UT fails to extend rules
of FOR and * instructions on the OOD test set while the
S2G-ACNN does so on some examples as shown in Fig-
ure 7. These are surprising in that both the seq2grid module
and the ACNN grid decoder do linear time computations in
the input length.
bAbI QA Tasks
Given as natural language with the small number of vocab-
ulary about 170, the bAbI QA tasks (Weston et al. 2015)
test 20 types of simple reasoning abilities such as counting,
induction, deduction, and path-finding. A problem instance
consists of a story, a question, and the answer. Here, the
story contains supporting sentences about the answer and
distractors which are irrelevant sentences to the answer. We
formulate the bAbI QA tasks (Weston et al. 2015) in se-
∙∙∙
∙∙∙
∙∙∙
∙∙∙
Preprocessed Grid Input 2D TextCNN
west
Class Label Target
Cross-entropy
poolings
3×3
logit layer
2×2
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
∙∙∙
4×4
on the
is split
se).
lse
637)
ly pre-
FOR or
longer
Task 2. two-supporting-facts
hCLSi Where is the apple ? hSEPi Mary journeyed to the gar-
den . Sandra got the football there . Mary picked up the apple
there . Mary dropped the apple .
Task 17. basic-deduction
hCLSi What is gertrude afraid of ? hSEPi Wolves are afraid
of sheep . Gertrude is a wolf . Winona is a wolf . Sheep are
afraid of mice . Mice are afraid of cats . Cats are afraid of
sheep . Emily is a cat . Jessica is a wolf .
Task 19. path-finding
hCLSi How do you go from the garden to the office ? hSEPi
The kitchen is west of the office . The office is north of the
hallway . The garden is east of the bathroom . The garden is
south of the hallway . The bedroom is east of the hallway .
Figure 8: Input examples of the bAbI QA tasks.
structions, our S2G-ACNN achieves almost 70% accuracy,
implying that it does not randomly pick one branch between
two possible branches. For the non-linear operations, the
S2G-ACNN shows little understanding compared with the
UT on the ID test set. However, the UT fails to extend rules
of FOR and * instructions on the OOD test set while the
S2G-ACNN does so on some examples as shown in Fig-
ure 7. These are surprising in that both the seq2grid module
and the ACNN grid decoder do linear time computations in
the input length.
size: 4×8

34. Results: bAbI QA Tasks
¡ Our sequence-to-grid method makes bAbI tasks easier.
¡ TextCNN fail at almost all tasks.
34/36

35. Results: bAbI QA Tasks
¡ Our sequence-to-grid method makes bAbI tasks easier.
¡ TextCNN fail at almost all tasks.
¡ Our module can compress long inputs into grid inputs.
¡ 79 (average # of input tokens ) > 32 (# of the grid slots)
¡ Only necessary words along story arcs are selected.
¡ Our model does not need a complex and expensive memory.
35/36

36. Closing Remarks
¡ Our seq2grid module:
- Input preprocessor.
- It automatically aligns an sequential input into a grid.
- During training, it requires no supervision for the alignment.
- Its nest list operations ensure the joint training of the module and the
grid decoder.
- It enhances neural networks in various symbolic reasoning tasks.
¡ Code: https://github.com/segwangkim/neural-seq2grid-module
¡ Contact: ksk5693@snu.ac.kr
36/36