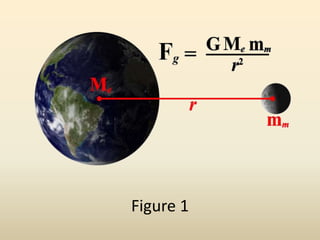
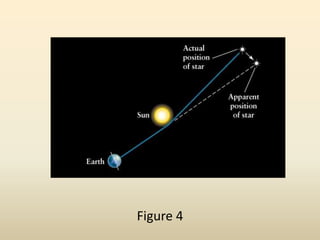
This document compares Newton and Einstein's theories of gravity. Newton's theory stated that gravity is an instantaneous force between objects, but it failed to explain observations like Mercury's orbit. Einstein's theory of general relativity improved upon Newton by stating that gravity is the curvature of spacetime caused by massive objects. Some successful tests of Einstein's theory included the bending of light and explaining Mercury's perihelion precession.

1. Gravity
Newton vs. Einstein
By
Halo Anwar Abdulkhalaq
Sep 2015

2. Overview
• Aim of the seminar
• Introduction
• Newton’s theory gravity
• Newton’s failure
• Einstein’s theory of gravity
• The successful tests of Einstein theory

3. 1. Aim of the seminar
The Aim of this seminar is studying the gravity in
two important theories (Newtonian and General
relativity). By the end of the seminar we should be able
to recognise both theories and be able to understand
the failure of Newton’s theory and the need to
Einstein’s correction.

4. 2.Introduction
• Throughout the history of physics there were
many attempts to understand natural forces in
the Universe.
• Gravity is one of the four fundamental forces
exist in nature and it is the weakest one
• Newton published the idea of gravity in his
book ‘’ the Principa’’ on 5th of July 1687.
• While Einstein published his famous paper on
general relativity theory in November 1915.

5. 3.Newton’s theory of gravity
• states that any two objects exert a gravitational force of
attraction on each other. The magnitude of the force is
proportional to the product of the gravitational masses
of the objects, and inversely proportional to the square
of the distance between them (fig. 1). For example in
the case of Earth and moon it is given as:
G: is universal gravitational constant = 6.67 x 10-11 N m 2 /kg 2
2
r
mM
GF me
grav 

6. Figure 1

7. • In the case of an object on earth the force of
gravity is given as:
it can be written as:
where Me = 5.98 x 1024 kg is the mass of the Earth
and Re = 6.38 x 106 m is the radius of the earth hence:
2
e
e
grav
R
mM
GF 
mgFgrav 
22
8.9
s
m
R
M
Gg
e
e


8. 4. Newton’s failure
• Newton claimed, gravity was a constant,
instantaneous force, the information about a sudden
change of mass would have to be somehow
communicated across the entire universe at once.
• And even the action between two very distant
masses would happen faster than the velocity of light
which is ultimate speed exist in the Universe and
nothing would exceed that speed according to
Einstein.
• The light from sun takes 8 minutes to reach earth,
but according to Newton if Sun disappears we on
earth feel it instantaneously.

9. 5. Einstein’s theory of gravity
• Einstein states that the gravity is geometry
through his famous equation (the Einstein
field equations), more specifically he says the
curvature of spacetime is gravity.
• The idea is that the massive objects in the
Universe warp spacetime and produce a
curvature around themselves which let the
other small particles to move according to it.

10. The path that each body takes in the curved spacetime
is called geodesic, and the body moves according to
geodesic equation which is equivalent to equation of
motion in classical mechanics.

11. Einstein Field Equations:
• is Einstein tensor which describes the
geometry of spacetime, G is Newtonian constant.
• is stress-energy tensor which describes the
properties of matter.
• It is easy to notice that this equation is linking
geometry to matter as Einstein himself claims.
G
T
 RgRG
2
1


12. • In this formula matter tells geometry how to be and
geometry tells matter how to move (fig. 2,3)
• Einstein tensor ( ) completely depends on
geometry of spacetime:
depends on which is Recci tensor and it
depends on a spacetime connection ( ) this
comes from spacetime metric
*
*
*
G
G R
 

         












  ,,R
  )(
2
1
,,, 

 gggg 

 dxdxgds 2

13. Figure 2

14. Figure 3

15. 6. The successful tests of Einstein theory
• Every theory goes under tests to examine its success,
Einstein’s general relativity theory (Gravity theory)
passed many tests successfully in the macro scales.
• One of those tests is bending of light, as it was
believed that light is move in the straight path but
Einstein corrected this and stated that even light will
follow the path on the curved spacetime produced by
massive objects (fig. 4)
• Another test was a perihelion precession of mercury
(fig.5), Newton formula was not precise to explain this
problem in exact way.

16. • On the other hand Einstein’s formula was successful to
find this precession.
• The relativistic precession is given by
Where (a) is semimajor axis, (T) is period and (e) is
eccentricity of Mercury’s orbit. (c) is speed of light.
• The precession observationally is (5600 arcsec/century),
Einstein’s theoretical value was exactly the same, while
Newton’s value was (5557 arcsec/century)
)1(
24
22
23
ecT
a
precession




17. Figure 4

18. Figure 5

19. References
1. Carroll, S., lecture note on general relativity,
http://arxiv.org/pdf/gr-qc/9712019.pdf
2. http://physics.ucr.edu/~wudka/Physics7/Notes_www/node9
8.html
3. http://theory.uwinnipeg.ca/physics/circ/node7.html
4. Pollock, C., Mercury’s Perihelion, 2003.