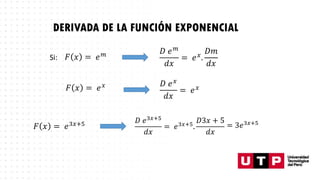
The document provides instructions on how to take derivatives of various functions using basic derivative rules. It includes examples of deriving exponential, logarithmic, and composite functions. Students are asked to find the derivatives of several example functions provided.

1. MATEMÁTICAS PARA LOS NEGOCIOS 2

2. Datos/Observaciones
Al finalizar la sesión de aprendizaje el alumno. Realiza derivadas
mediante reglas básicas de derivación.

3. Derivada de una Función Constante:

4. Regla de las Potencias:

5. Regla del producto de una constante por la función:

6. Regla de la suma o diferencia de funciones

7. Regla de la suma o diferencia de funciones

8. Resolver:
Derive 𝑓 𝑥 = 3 𝑥 +
2
𝑥3 − 𝑥5 +
3
5

9. Cuanto Aprendiste?
D𝑒𝑟𝑖𝑣𝑒: 𝑓 𝑥 = 5 + 3𝑥 − 2𝑥2 +
5
𝑥4

10. 𝑆í 𝑓 𝑥 𝑦 𝑔 𝑥 𝑠𝑜𝑛 𝑑𝑒𝑟𝑖𝑣𝑎𝑏𝑙𝑒𝑠 𝑠𝑢 𝑝𝑟𝑜𝑑𝑢𝑐𝑡𝑜 𝑡𝑎𝑚𝑏𝑖𝑒𝑛 𝑒𝑠 𝑑𝑒𝑟𝑖𝑣𝑎𝑏𝑙𝑒
𝐷𝑓 𝑥 𝑔(𝑥)
𝑑𝑥
= 𝑓 𝑥 𝑔′ 𝑥 + 𝑔 𝑥 𝑓′(𝑥)

11. 𝑆𝑒𝑎 𝑓 𝑥 = 5 − 3𝑥 + 𝑥2 𝑦 𝑔 𝑥 = 𝑥3 + 4
𝐻𝑎𝑙𝑙𝑒 𝑙𝑎 𝑑𝑒𝑟𝑖𝑣𝑎𝑑𝑎 𝑑𝑒 𝑓 𝑥 . 𝑔 𝑥
𝐷𝑓 𝑥 𝑔(𝑥)
𝑑𝑥
= 𝑓 𝑥 𝑔′
𝑥 + 𝑔 𝑥 𝑓′(𝑥) …….*
𝑓 𝑥 = 5 − 3𝑥 + 𝑥2 → 𝑓′ 𝑥 = −3 + 2𝑥
𝑔 𝑥 = 𝑥3
+ 4 → 𝑔′
𝑥 = 3𝑥2
Reemplazando en (*) (5 − 3𝑥 + 𝑥2
)(3𝑥2
) + (𝑥3
+ 4)(−3 + 2𝑥)
15𝑥2 − 9𝑥3 + 3𝑥4 − 3𝑥3 − 12 + 2𝑥4 + 8𝑥
𝑹𝒑𝒕𝒂. 5𝑥4 − 12𝑥3 + 15𝑥2 + 8𝑥 − 12

12. 𝑆𝑒𝑎 𝑓 𝑥 = 𝑥3/2 + 3𝑥 − 6 𝑦 𝑔 𝑥 = 𝑥4 + 4𝑥2 + 8
𝐻𝑎𝑙𝑙𝑒 𝑙𝑎 𝑑𝑒𝑟𝑖𝑣𝑎𝑑𝑎 𝑑𝑒 𝑓 𝑥 . 𝑔 𝑥

13. 𝑆í 𝑓 𝑥 𝑦 𝑔 𝑥 𝑠𝑜𝑛 𝑑𝑒𝑟𝑖𝑣𝑎𝑏𝑙𝑒𝑠 𝑠𝑢 𝑐𝑜𝑐𝑖𝑒𝑛𝑡𝑒 𝑡𝑎𝑚𝑏𝑖𝑒𝑛 𝑒𝑠 𝑑𝑒𝑟𝑖𝑣𝑎𝑏𝑙𝑒,
𝐷
𝑓 𝑥
𝑔(𝑥)
=
𝑔(𝑥)𝑓′ 𝑥 + 𝑓(𝑥)𝑔′ 𝑥
{𝑔 𝑥 }2
𝑆𝑖𝑒𝑚𝑝𝑟𝑒 𝑞𝑢𝑒 𝑔 𝑥 ≠ 0

14. 𝑆𝑒𝑎 𝑓 𝑥 = 𝑥2 + 4𝑥 + 8 𝑦 𝑔 𝑥 = 𝑥3 + 4𝑥 − 2
𝐻𝑎𝑙𝑙𝑒 𝑙𝑎 𝑑𝑒𝑟𝑖𝑣𝑎𝑑𝑎 𝑑𝑒
𝑓 𝑥
𝑔(𝑥)
𝐷
𝑓 𝑥
𝑔(𝑥)
=
𝑔 𝑥 𝑓′ 𝑥 −𝑓 𝑥 𝑔′(𝑥)
{𝑔 𝑥 }2 …….*
𝑓 𝑥 = 𝑥2 + 4𝑥 + 8 → 𝑓′ 𝑥 = 2𝑥 + 4
𝑔 𝑥 = 𝑥3 + 4𝑥 − 2 → 𝑔′ 𝑥 = 3𝑥2 + 4
Reemplazando en (*) (𝑥3 + 4𝑥 − 2)(2𝑥 + 4) − (𝑥2 + 4𝑥 + 8)(3𝑥2 + 4)
{𝑥3 + 4𝑥 − 2}2
2𝑥4 + 8𝑥2 − 4𝑥 + 4𝑥3 + 16𝑥 − 8 − 3𝑥4 − 12𝑥3 − 24𝑥2 − 4𝑥2 − 16𝑥 − 32
{𝑥3 + 4𝑥 − 2}2
Rpta:
−𝑥4−8𝑥3−20𝑥2−20𝑥−40
{𝑥3+4𝑥−2}2

15. Ejercicio Explicativo:
𝑆𝑒𝑎 𝑓 𝑥 = 3 − 𝑥2 𝑦 𝑔 𝑥 = 𝑥2 − 3𝑥 + 6
𝐻𝑎𝑙𝑙𝑒 𝑙𝑎 𝑑𝑒𝑟𝑖𝑣𝑎𝑑𝑎 𝑑𝑒
𝑓 𝑥
𝑔(𝑥)
+ f x . g(x)

16. 𝑆𝑒𝑎 𝑓 𝑥 = 3𝑥 − 2𝑥2
− 2 𝑦 𝑔 𝑥 = 4𝑥2
− 𝑥 + 2
𝐻𝑎𝑙𝑙𝑒 𝑙𝑎 𝑑𝑒𝑟𝑖𝑣𝑎𝑑𝑎 𝑑𝑒
𝑔 𝑥
𝑓(𝑥)
¿Cuánto aprendiste?

17. Dada la función 𝒇 𝒙 = 𝐥𝐧 𝒖 , 𝑑𝑜𝑛𝑑𝑒 𝑢 𝑒𝑠 𝑓𝑢𝑛𝑐𝑖ó𝑛 𝑑𝑒 "𝑥",luego:
𝒅𝒇(𝒙)
𝒅𝒙
=
𝒅 𝐥𝐧 𝒖
𝒅𝒙
=
𝟏
𝒖
.
𝒅𝒖
𝒅𝒙
Se entiende como: “La derivada del logaritmo natural de una función
es igual a la derivada de la función dividida por la función”
Caso particular:
𝒅
𝒅𝒙
𝐥𝐧 𝒙 =
𝟏
𝒙

18. Dada la función 𝒇 𝒙 = 𝒍𝒐𝒈𝒂 𝒖 , donde “u” es una función de “x”,
luego:
𝒅
𝒅𝒙
𝒍𝒐𝒈𝒂 𝒖 =
𝟏
𝒙∗𝒍𝒏 𝒂
*
𝒅𝒖
𝒅𝒙
Caso Particular:
𝒅
𝒅𝒙
𝐥𝐨𝐠𝒂 𝒙 =
𝟏
𝒙 ∗ 𝐥𝐧 𝒂

19. 1. 𝐻𝑎𝑙𝑙𝑎𝑟
𝑑𝑓
𝑑𝑥
siendo 𝑓 𝑥 = 𝑥3 ∗ ln 𝑥
Solución:
Aplicamos: f′ x = u′ ∗ v + u ∗ v′
𝑓′ 𝑥 = 𝑥3 ′ ∗ ln 𝑥 + 𝑥3 ∗ ln 𝑥 ′
𝑓′ 𝑥 = 3𝑥2 ∗ ln 𝑥 + 𝑥3 ∗
1
𝑥
𝑓′ 𝑥 = 3𝑥2 ∗ ln 𝑥 + 𝑥2
𝑓′ 𝑥 = 𝑥2 3 ln 𝑥 + 1 … 𝑅𝑝𝑡𝑎

20. 02. 𝐻𝑎𝑙𝑙𝑎𝑟
𝑑𝑓
𝑑𝑥
siendo 𝑓 𝑥 = 𝑥/ ln 𝑥
SOLUCIÓN: Aplicamos:
𝑓 𝑥 =
𝑢
𝑣
; 𝑓′
𝑥 =
𝑣 ∗ 𝑢′ − 𝑢 ∗ 𝑣′
𝑣2
𝑓′ 𝑥 =
(ln 𝑥) ∗ 𝑥 ′
− 𝑥 ∗ (ln 𝑥)′
ln 𝑥 2
𝑓′ 𝑥 =
(ln 𝑥) ∗ (1) − 𝑥 ∗ (
1
𝑥
)
ln 𝑥 2
𝑓′
(𝑥) =
ln 𝑥 − 1
ln 𝑥 2 … . 𝑅𝑝𝑡𝑎.

21. 03. 𝐻𝑎𝑙𝑙𝑎𝑟
𝑑𝑓
𝑑𝑥
siendo 𝑓 𝑥 = 𝑥1/2
∗ ln 𝑥
SOLUCIÓN: Aplicamos:
𝑓 𝑥 = 𝑢 ∗ 𝑣 ; 𝑓′
𝑥 = 𝑢′
∗ 𝑣 + 𝑢 ∗ 𝑣′
𝑓′(𝑥) = 𝑥
1
2
′
∗ (ln 𝑥) + 𝑥
1
2 ∗ ln 𝑥 ′
𝑓′
(𝑥) =
1
2
𝑥−
1
2 ∗ (ln 𝑥) + 𝑥
1
2 ∗
1
𝑥
𝑓′
(𝑥) =
1
2
𝑥−
1
2 ∗ (ln 𝑥) + 𝑥−
1
2
𝑓′
(𝑥) =
ln 𝑥 + 2
2 𝑥
… . 𝑅𝑝𝑡𝑎.

22. 04. 𝐻𝑎𝑙𝑙𝑎𝑟
𝑑𝑓
𝑑𝑥
siendo 𝑓 𝑥 = ln 𝑥3 − 2𝑥
SOLUCIÓN: Aplicamos:
𝒅𝒇(𝒙)
𝒅𝒙
=
𝟏
𝒖
.
𝒅𝒖
𝒅𝒙
𝑓′ 𝑥 =
1
(𝑥3 − 2𝑥)
∗ 𝑥3 − 2𝑥 ′
𝑓′ 𝑥 =
1
(𝑥3 − 2𝑥)
∗ 3𝑥2 − 2
𝑓′ 𝑥 =
3𝑥2
+ 2
𝑥3 − 2𝑥
… . 𝑅𝑝𝑡𝑎.

23. Cuanto aprendiste?
𝐻𝑎𝑙𝑙𝑎𝑟
𝑑𝑓
𝑑𝑥
siendo 𝑓 𝑥 = 𝑥 log2 𝑥 − 𝑙𝑜𝑔𝑥. ln 𝑥
𝐻𝑎𝑙𝑙𝑎𝑟
𝑑𝑓
𝑑𝑥
siendo 𝑓 𝑥 =
log5 𝑥
ln(𝑥+1)
+ log(𝑥 − 4). ln 𝑥

24. DERIVADA DE LA FUNCIÓN EXPONENCIAL
Si:
𝐹 𝑥 = 𝑒𝑥 𝐷 𝑒𝑥
𝑑𝑥
= 𝑒𝑥
𝐹 𝑥 = 𝑒𝑚 𝐷 𝑒𝑚
𝑑𝑥
= 𝑒𝑥
.
𝐷𝑚
𝑑𝑥
𝐹 𝑥 = 𝑒3𝑥+5 𝐷 𝑒3𝑥+5
𝑑𝑥
= 𝑒3𝑥+5.
𝐷3𝑥 + 5
𝑑𝑥
= 3𝑒3𝑥+5

25. DERIVADA DE LA FUNCIÓN EXPONENCIAL
Si:
𝐹 𝑥 = 3𝑥 𝐷 3𝑥
𝑑𝑥
= 3𝑥
. 𝑙𝑛3
𝐹 𝑥 = 𝑎𝑚
𝐷 𝑎𝑚
𝑑𝑥
= 𝑎𝑥
.
𝐷𝑚
𝑑𝑥
. 𝑙𝑛𝑎
𝐹 𝑥 = 27𝑥−3 𝐷 27𝑥−3
𝑑𝑥
= 27𝑥−7.
𝐷7𝑥 − 3
𝑑𝑥
. 𝑙𝑛2 = 7. 27𝑥−3. ln2

26. EJERCICIO EXPLICATIVO
𝐹 𝑥 = 3𝑒−4𝑥
+ 2(3−𝑥)
Derivar:
𝐹 𝑥 = 𝑒(2−5𝑥) − 5(2𝑥+13)

27. Cuanto aprendiste?
Derive 𝑓 𝑥 = 𝑒2𝑥 log2 𝑥 − 3𝑥. ln 𝑥