More Related Content
PPTX
PDF
PPTX
PDF
PDF
DOCX
PDF
PDF
What's hot
PDF
PPTX
PDF
PDF
PDF
PDF
PDF
PPTX
PDF
PDF
PyMCがあれば,ベイズ推定でもう泣いたりなんかしない PDF
PDF
PPTX
Structural data analysis based on multilayer networks PDF
(2020.10) 分子のグラフ表現と機械学習: Graph Neural Networks (GNNs) とは? PDF
PPTX
PDF
Bayes Independence Test - HSIC と性能を比較する- PDF
PDF
PDF
Viewers also liked
PPTX
PDF
2014/06/13 若手Webエンジニア交流会発表資料「博士課程の新卒エンジニアがデータ分析環境を作った話」 PPTX
PDF
PDF
PPTX
PDF
PDF
Similar to SEM分析の理論
DOCX
PDF
PDF
2011建築研究賞_最適化手法を用いた建物の同定問題_08N1002青山仁美/08N1038小祝碧_吉田研 PDF
PPT
PDF
テキストマイニングで発掘!? 売上とユーザーレビューの相関分析 KEY
第5章 統計的仮説検定 (Rによるやさしい統計学) PDF
PDF
Datamining 8th Hclustering PDF
PDF
Model sminar100710 iwasaki PPTX
PPTX
PDF
PDF
PDF
Normalization of microarray PDF
PDF
DOCX
PDF
More from Daisuke Sashida
PPTX
ソーシャルメディア情報のユーザ行動変容に対する影響と情報拡散要因の明確化 PPTX
The proposal of the viral model of information which is considering social me... PPTX
PPTX
PPTX
PPT
SEM分析の理論
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
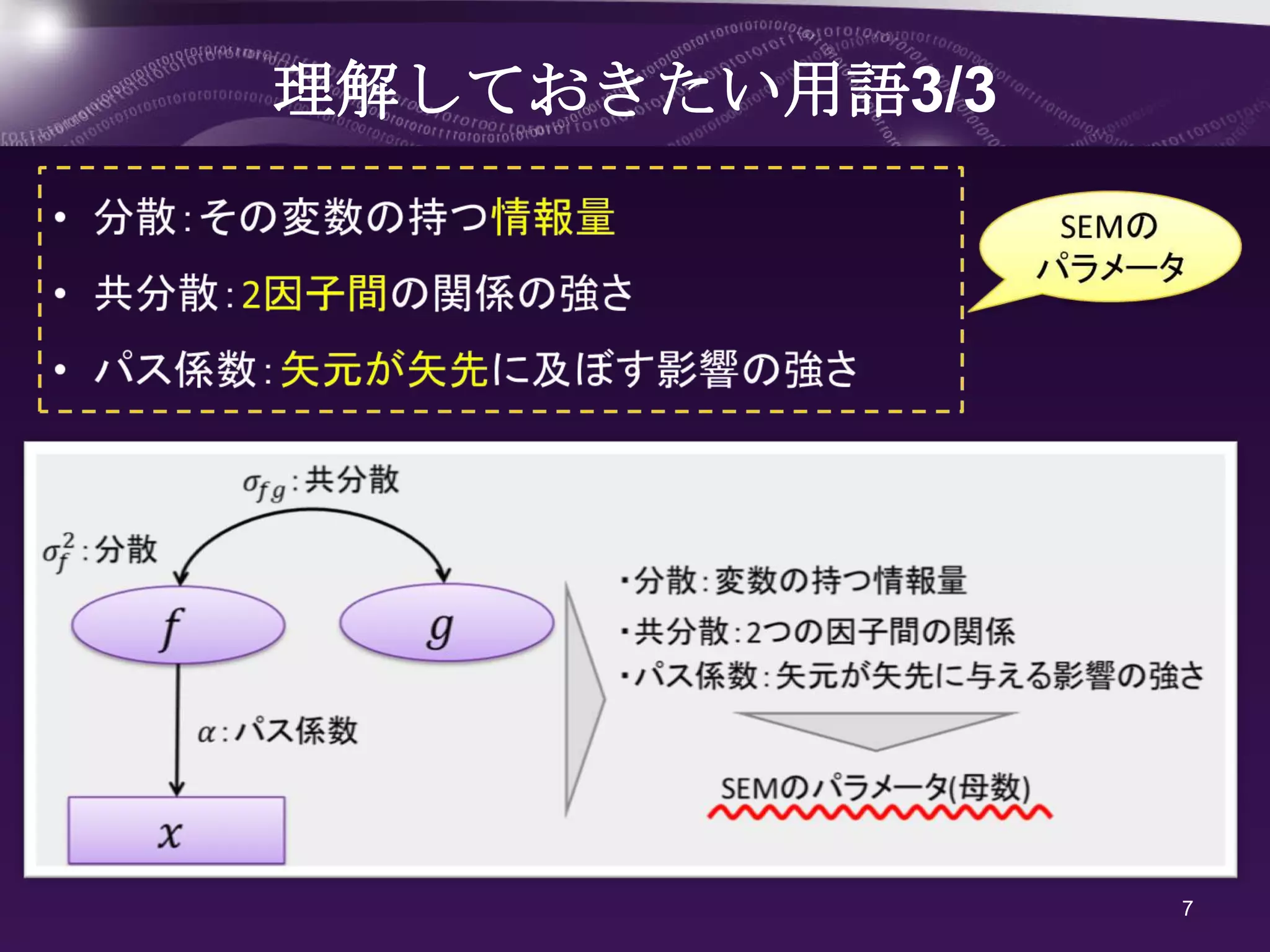
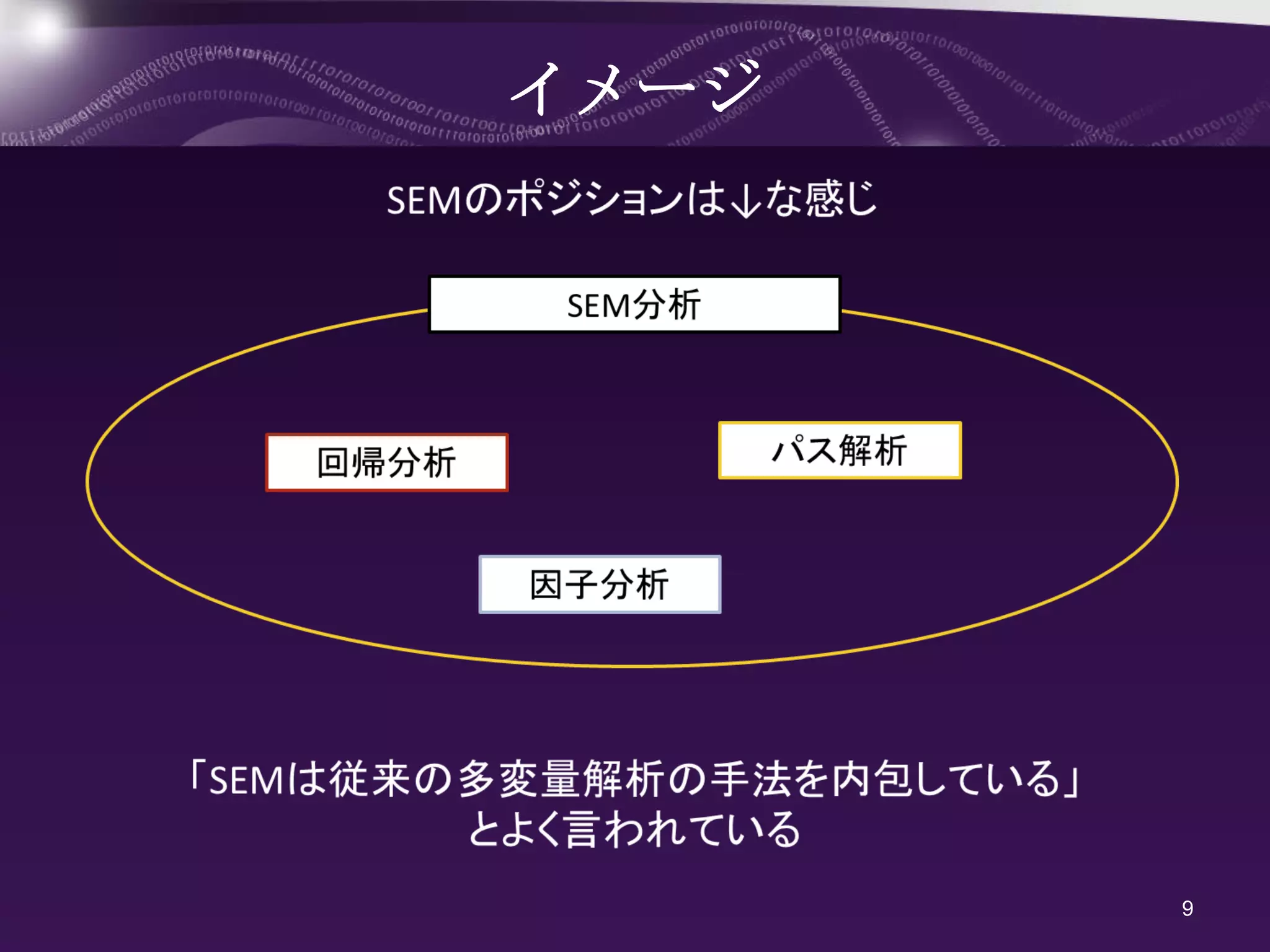
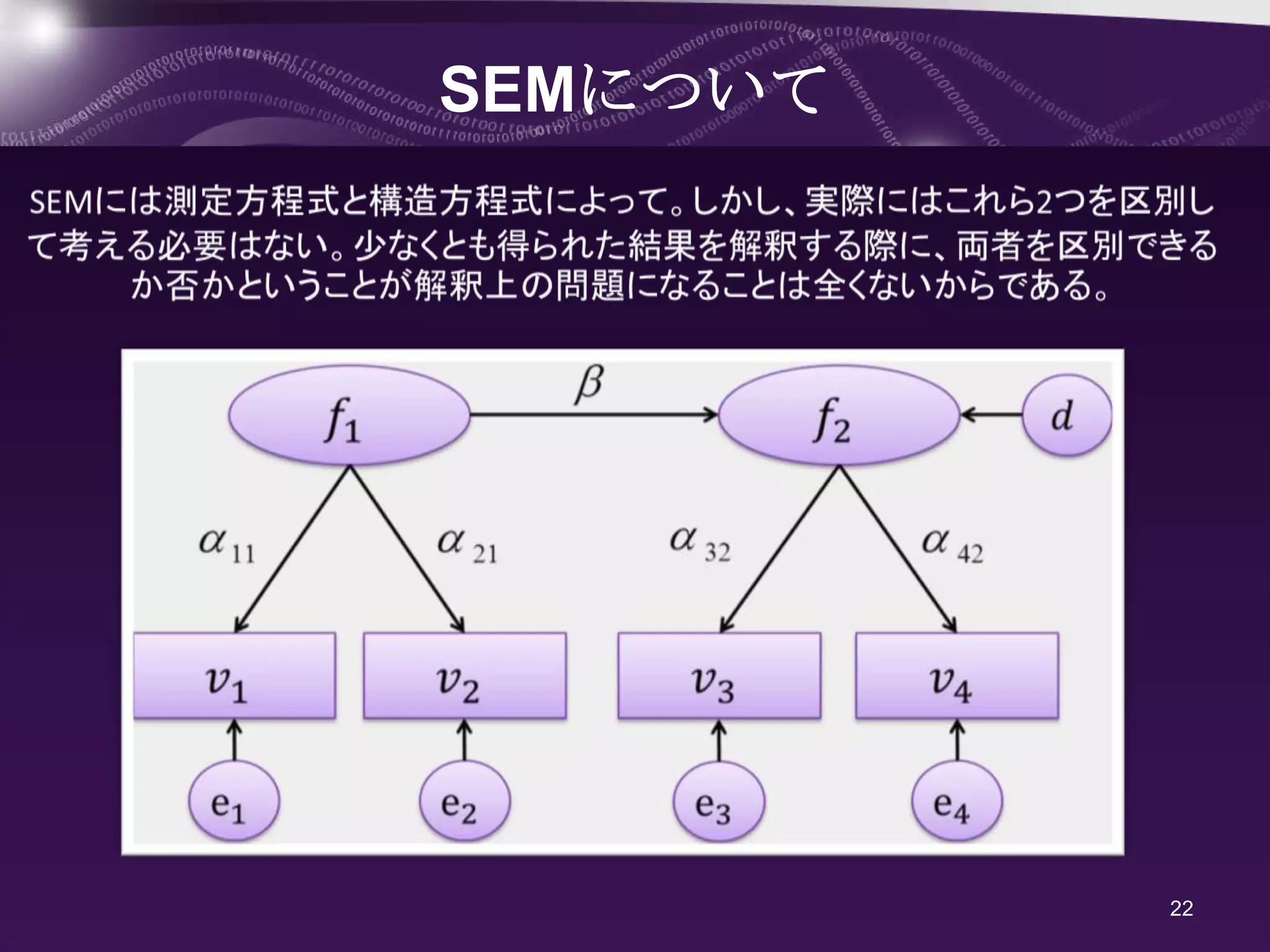
SEMについて
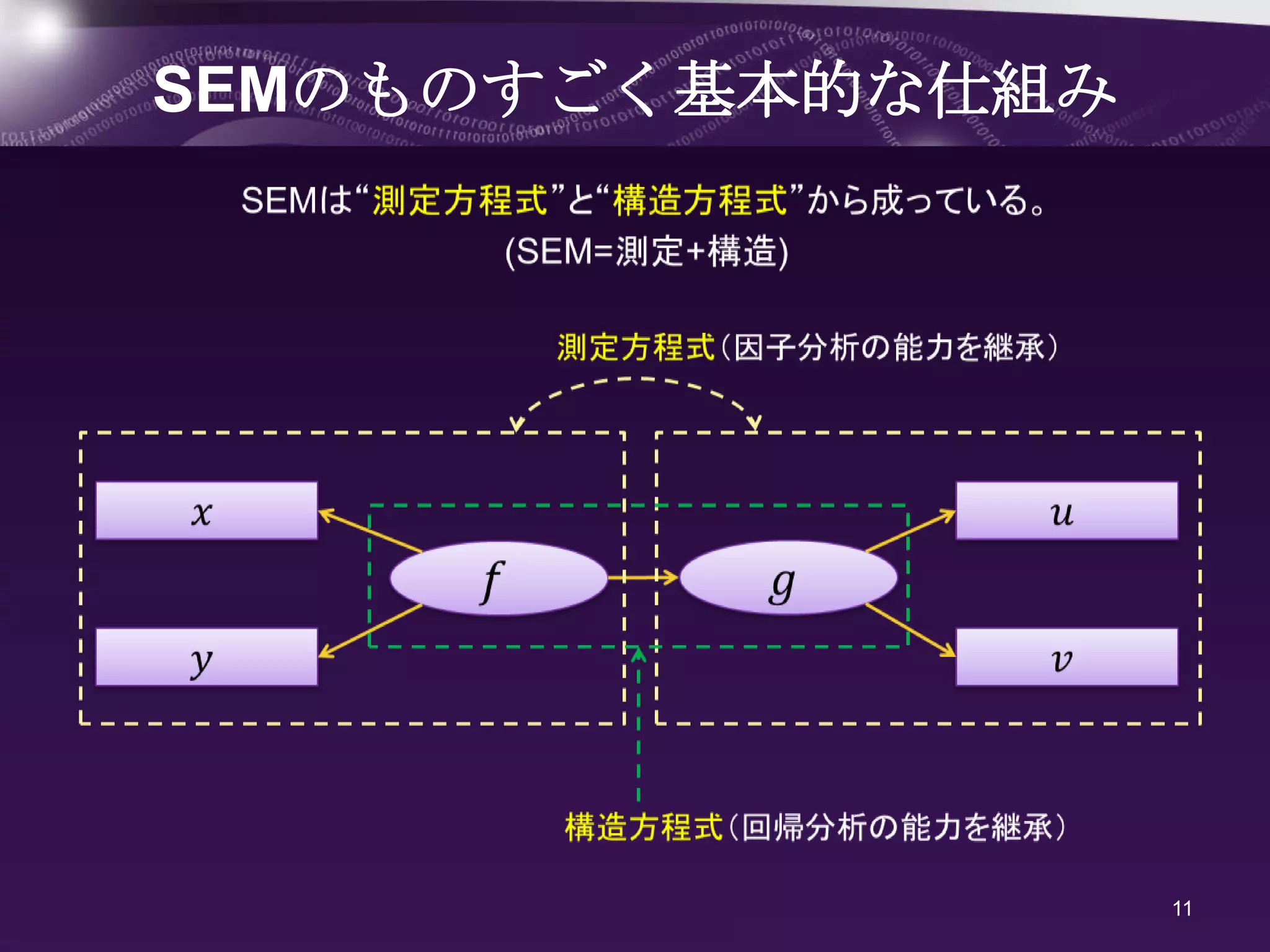
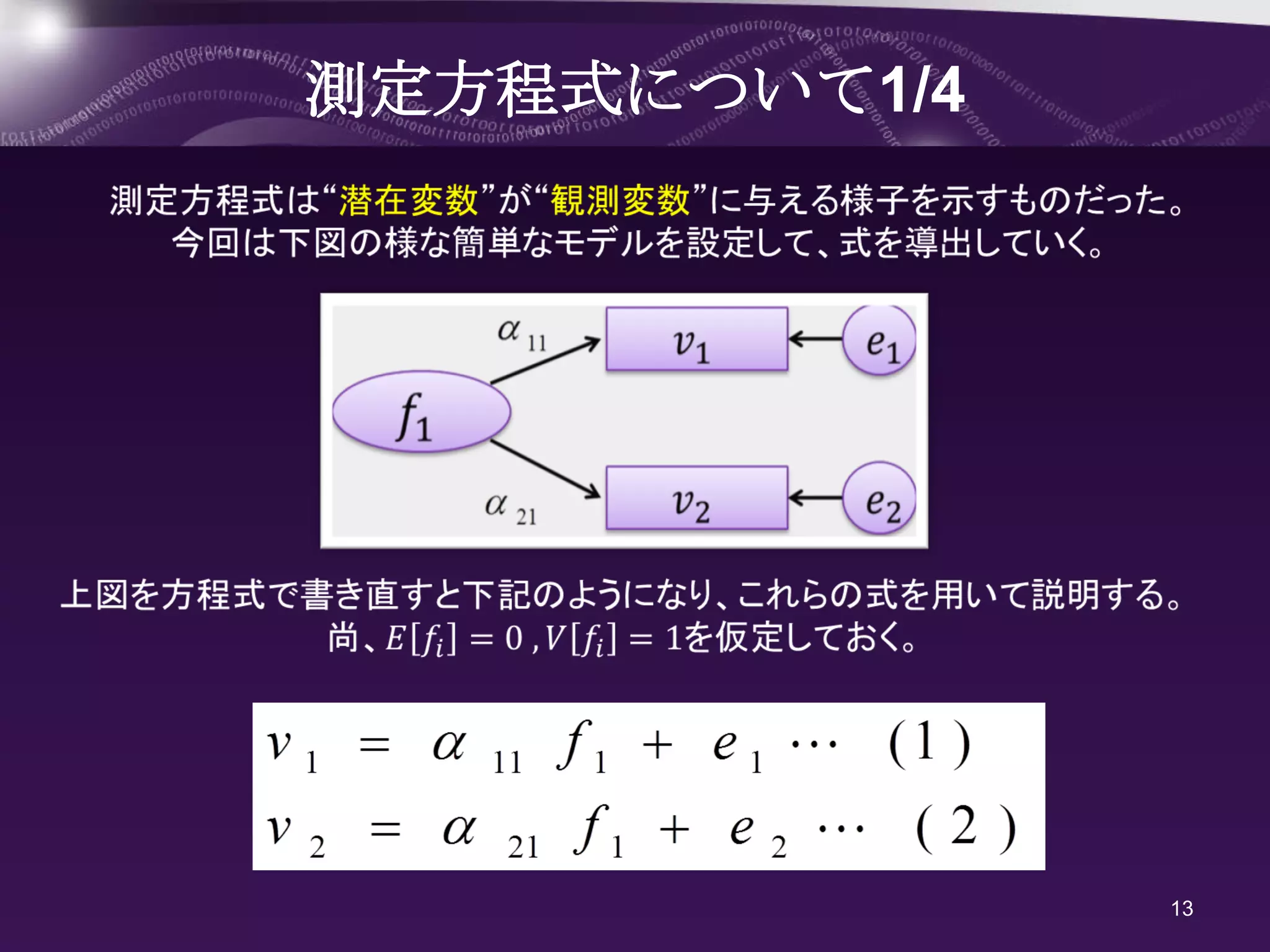
パス図を方程式で表すと
こんな感じ
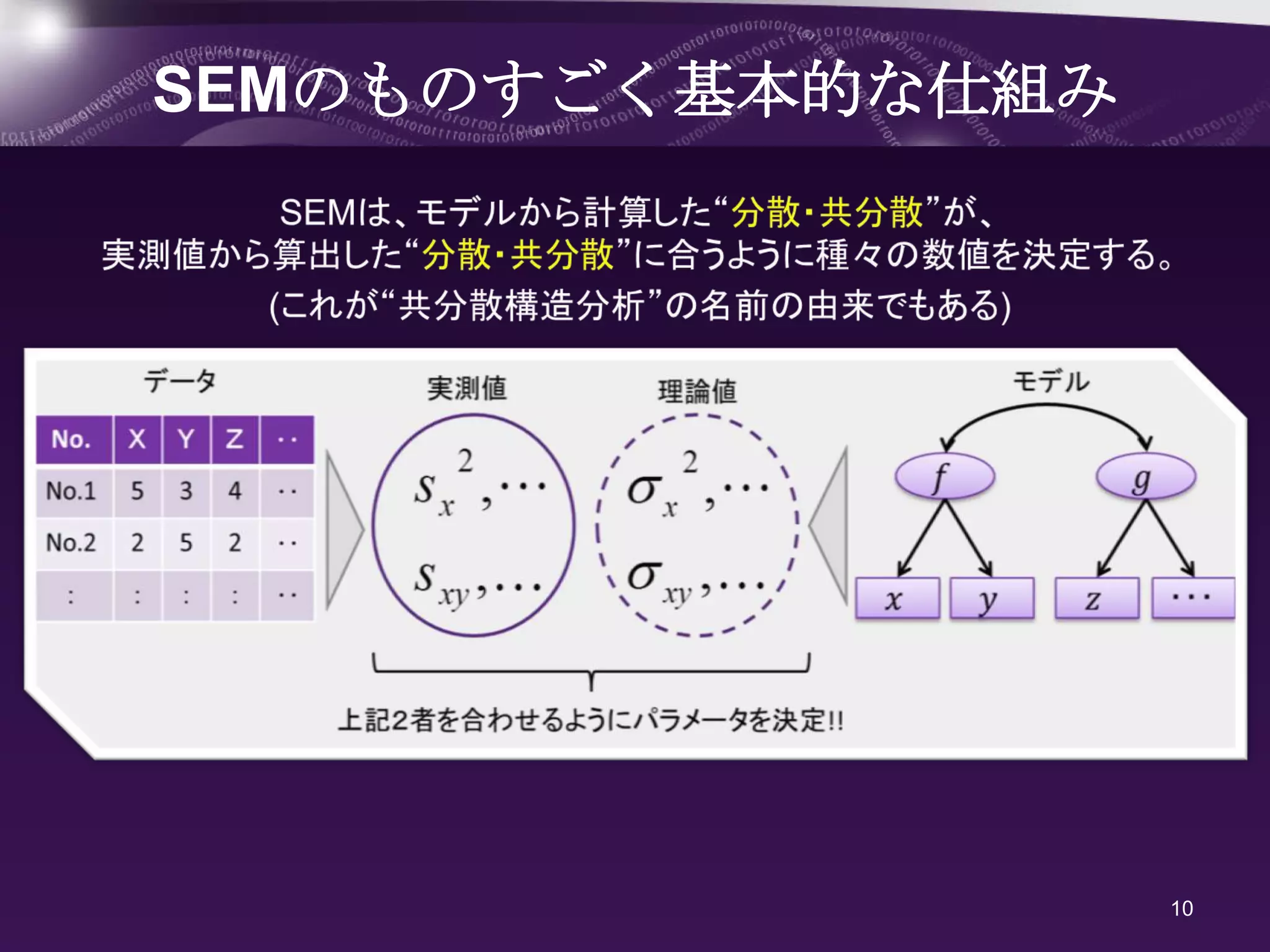
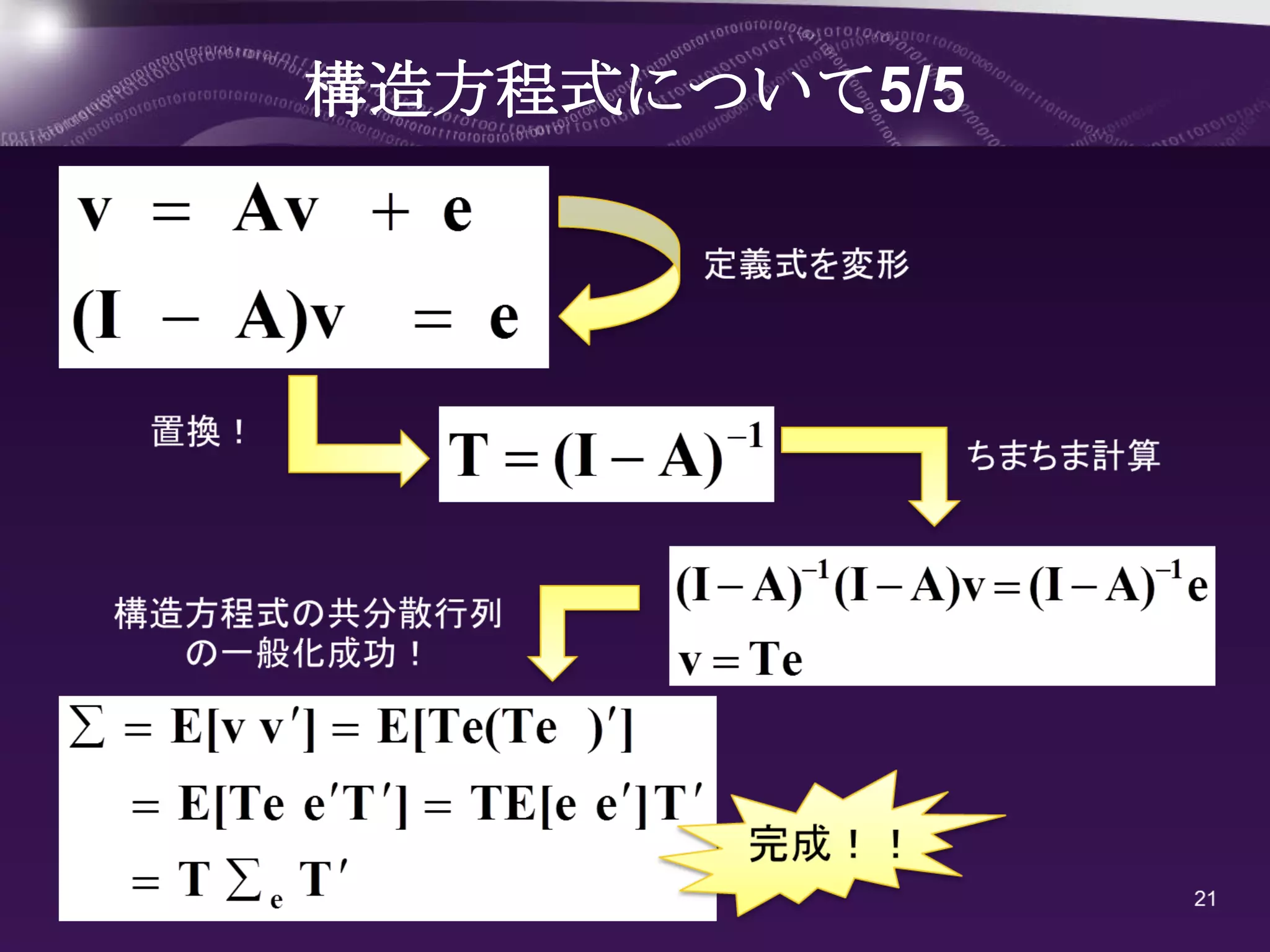
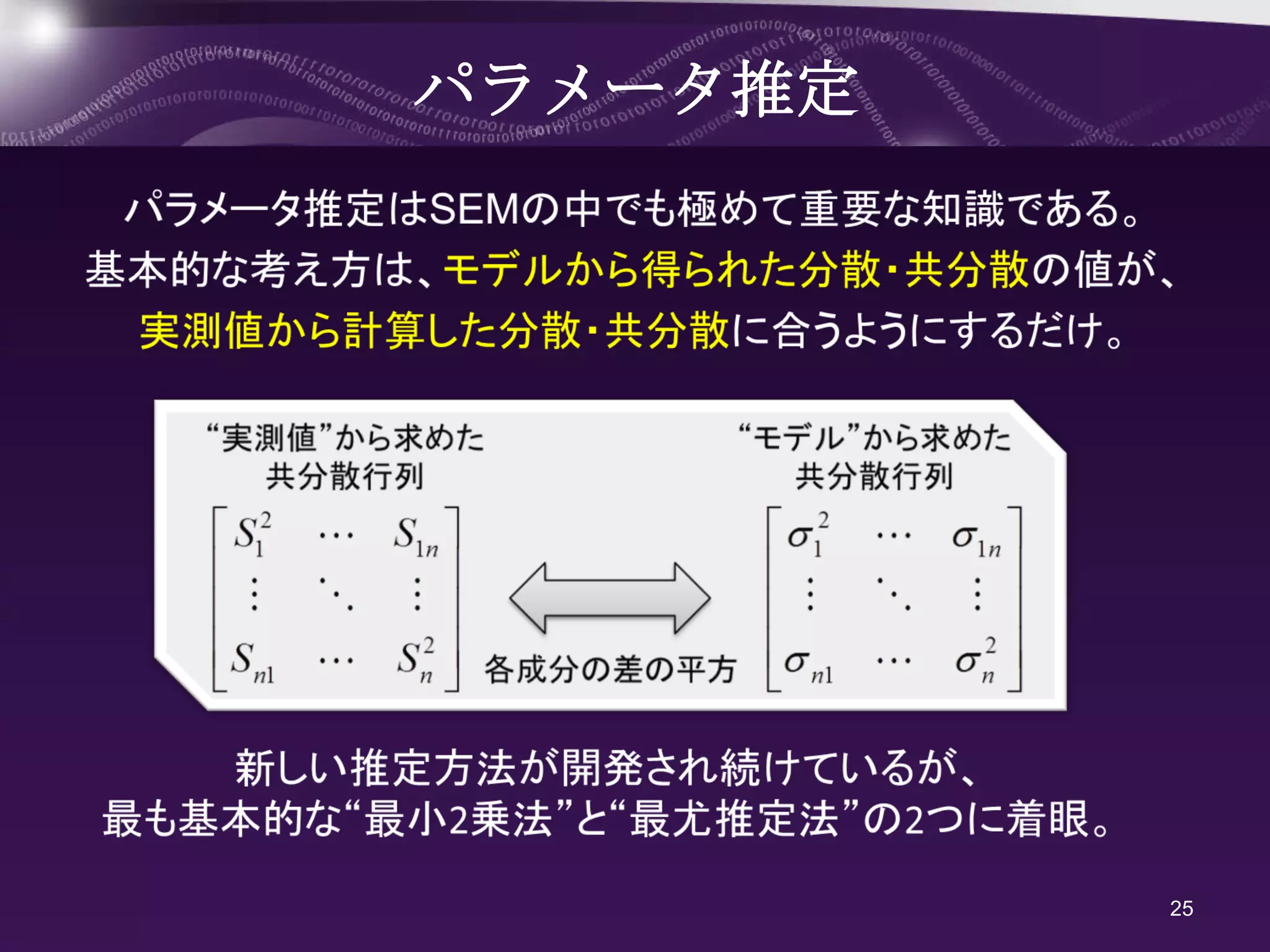
分散・共分散の導出手順は従来と同様なので結果のみを示す。
2 2 2
11 1 e1
2 2 2 2
21 11 1 21 1 e2
2 2 2 2 2 2 2 2
32 11 21 1 32 21 21 1 32 21 1 32 d e3
2 2 2 2 2 2 2 2 2 2 2
42 21 21 1 42 21 21 1 42 32 ( 21 1 d ) 42 21 1 42 d e3
24
- 25.
- 26.
- 27.
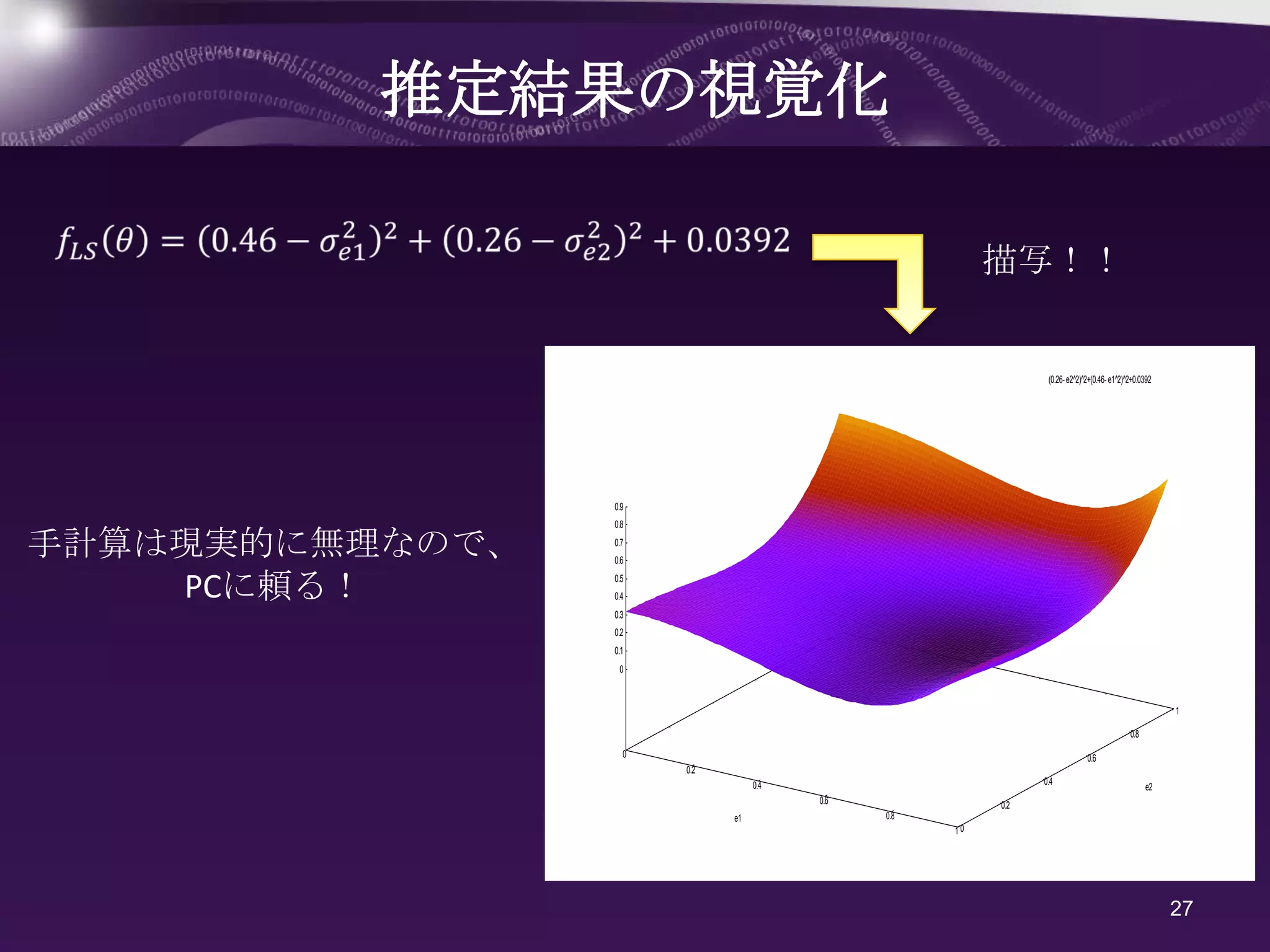
推定結果の視覚化
描写!!
(0.26- e2^2)^2+(0.46- e1^2)^2+0.0392
0.9
0.8
手計算は現実的に無理なので、 0.7
0.6
PCに頼る! 0.5
0.4
0.3
0.2
0.1
0
1
0.8
0 0.6
0.2
0.4 0.4
e2
0.6 0.2
e1 0.8
10
27
- 28.
- 29.
- 31.
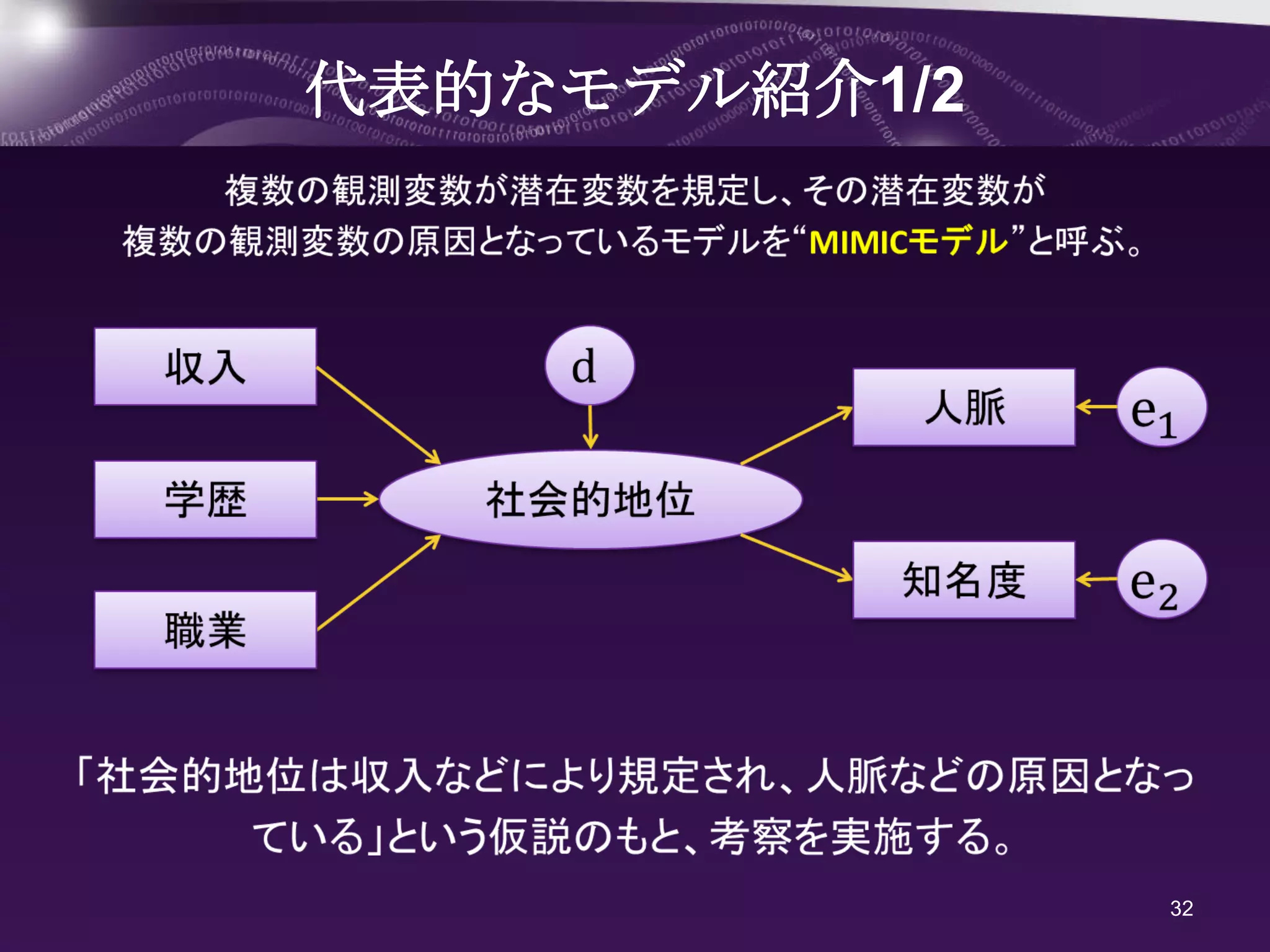
- 32.
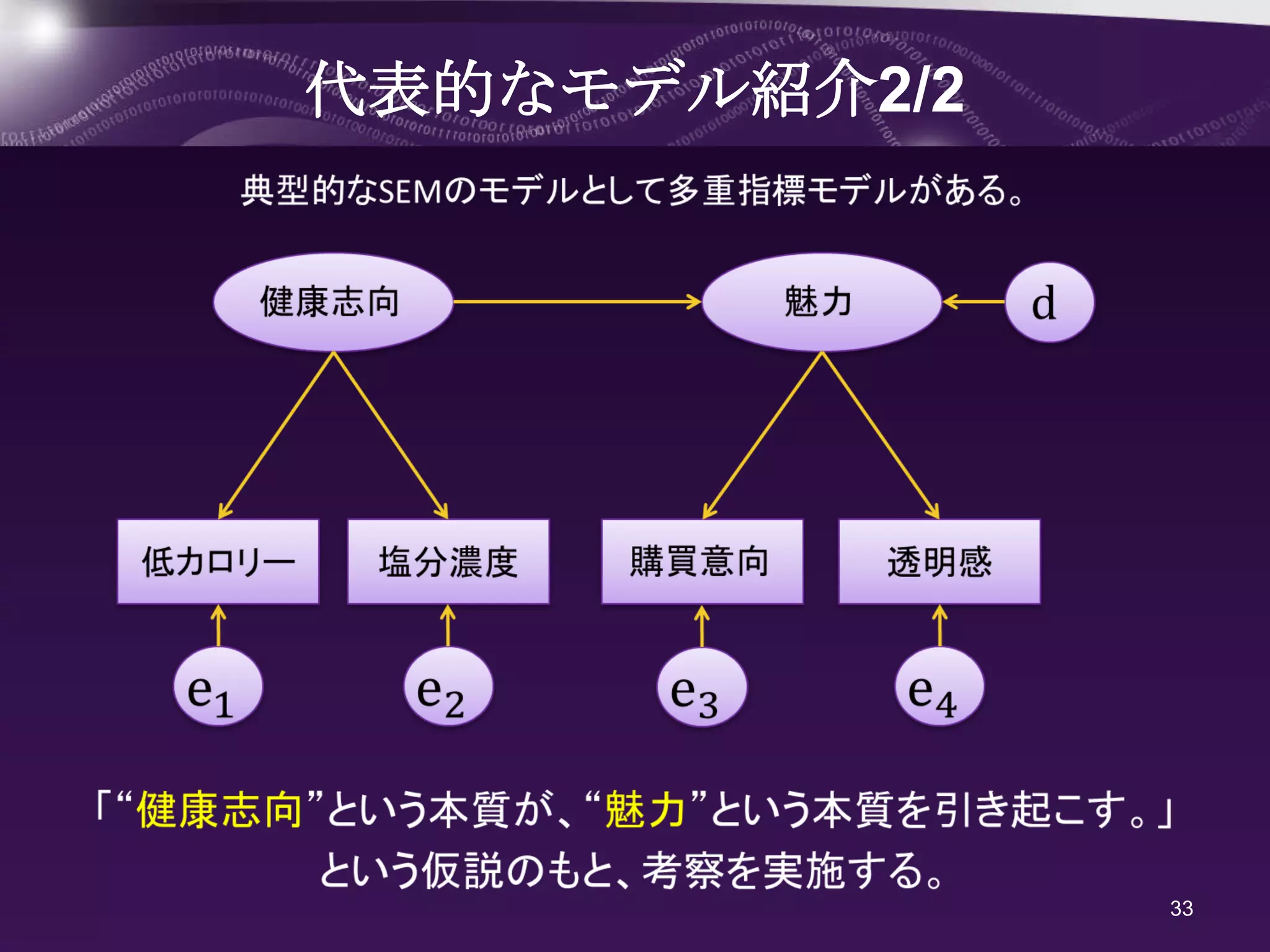
- 33.