Downloaded 261 times
Uploaded byDwi Kania
Sejarah Matematika
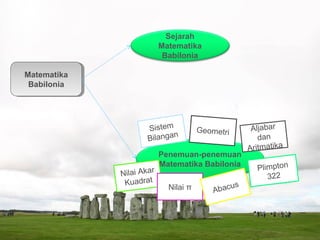
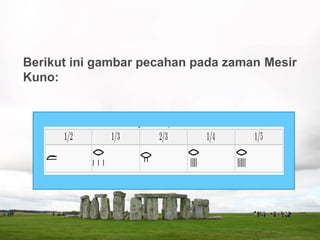
Dokumen ini membahas sejarah dan perkembangan matematika di Babilonia dan Mesir Kuno, termasuk sistem bilangan, geometri, aljabar, serta penemuan-penemuan penting seperti Plimpton 322 dan Papirus Rhind. Ia juga mencatat kontribusi tokoh-tokoh besar dalam sejarah matematika seperti Thales, Pythagoras, dan Archimedes. Selain itu, terdapat penjelasan mengenai teknik penghitungan dan penggunaan matematika dalam berbagai aspek kehidupan masyarakat kuno.
Sejarah Matematika
- 1. Oleh:Oleh: Dwi Kania Nur’aniDwiKania Nur’ani 0102030110049901020301100499 Dwi KaryantoDwi Karyanto 0102030110050001020301100500 Gita Ristya P.Gita Ristya P. 0102030110050701020301100507 MATEMATIKA BABILONIA DAN MESIR KUNO
- 2.
- 3. • Matematika Babiloniamerujuk pada seluruh matematika yangMatematika Babilonia merujuk pada seluruh matematika yang dikembangkan oleh bangsa Mesopotamia (kini Iraq) sejakdikembangkan oleh bangsa Mesopotamia (kini Iraq) sejak permulaan Sumeria hingga permulaan peradaban helenistik.permulaan Sumeria hingga permulaan peradaban helenistik. • Matematika Babilonia diturunkan dari lebih daripada 400 lempenganMatematika Babilonia diturunkan dari lebih daripada 400 lempengan tanah liat yang digali sejak 1850-an. Ditulis di dalam tulisan paku,tanah liat yang digali sejak 1850-an. Ditulis di dalam tulisan paku, lempengan ditulisi ketika tanah liat masih basah, dan dibakar dilempengan ditulisi ketika tanah liat masih basah, dan dibakar di dalam tungku atau dijemur di bawah terik matahari.dalam tungku atau dijemur di bawah terik matahari. • Bukti terdini matematika tertulis adalah karya bangsa Sumeria, yangBukti terdini matematika tertulis adalah karya bangsa Sumeria, yang membangun peradaban kuno di Mesopotamia. Merekamembangun peradaban kuno di Mesopotamia. Mereka mengembangkan sistem rumit metrologi sejak tahun 3000 SM.mengembangkan sistem rumit metrologi sejak tahun 3000 SM. BBangsa Sumeria menuliskan tabel perkalian pada lempengan tanahangsa Sumeria menuliskan tabel perkalian pada lempengan tanah liat dan berurusan dengan latihan-latihan geometri dan soal-soalliat dan berurusan dengan latihan-latihan geometri dan soal-soal pembagian. Jejak terdini sistem bilangan Babilonia juga merujukpembagian. Jejak terdini sistem bilangan Babilonia juga merujuk pada periode ini.pada periode ini. Sejarah Matematika Babilonia
- 4. Sistem Bilangan Matematika Babiloniaditulis menggunakan sistem bilangan seksagesimal (basis-60). Dari sinilah diturunkannya penggunaan bilangan 60 detik untuk semenit, 60 menit untuk satu jam, dan 360 (60 x 6) derajat untuk satu putaran lingkaran, juga penggunaan detik dan menit pada busur lingkaran yang melambangkan pecahan derajat.
- 5. • Ilmu geometrisudah dipelajari peradaban Babilonia (4000 SM - 500 SM). Geometri Babilonia berhubungan erat dengan pengukuran praktik yang dimaksudkan untuk bisa mendirikan berbagai bangunan yang kokoh dan besar. • Bangsa Babilonia mengembangkan cara mengitung luas dan volume. Ciri utama dari geometri Babilonia adalah bercorak aljabaris. G E O M E T R I
- 6. Aljabar dan Aritmatika •Diophantus merupakan “Bapak Aljabar” bagi Babilonia yang mengembangkan konsep-konsep aljabar Babilonia.
- 7.
- 8. • Terdapat 100masalah persamaan bikuadrat (pangkat empat) yang belum terpecahkan secara simultan, misalnya: xy = 600 ; 150 ( x – y ) – ( x + y )2 = -1000. Dan XY = a; yang terbentuk persamaan pangkat enam diubah kebentuk kuadrat pangkat tiga. • Neugebauer mendapatkan dua buah masalah deret yang sangat menarik pada tablet Louvre sekitar tahun 300 SM, yakni: 1 + 2 + 22 + . . . + 29 = 29 .29 – 1. Dan 12 + 22 + 32 + . . . + 102 = {1 + 10 } 55 = 385. • Di samping itu bangsa Babylonia sudah menggunakan rumus :
- 9. Nilai π • Kelilingsuatu lingkaran digunakan tiga kali diameternya, luas lingkaran digunakan seperduabelas dari kuadrat kelilingnya dengan π = 3.
- 10. Abacus • Abacus berasaldari bahasa yunani yaitu "Abax" atau "abakon" yang berarti meja. Abacus dalam bahasa Indonesia disebut sempoa. Abacus dikembangkan dari Salamis tablet, sebuah tabel penghitungan yang digunakan oleh bangsa babilonia, yang ditemukan pada tahun 1846 di kepulauan Salami.
- 11. Plimpton 322 • Mungkinhasil karya hebat dari matematika Babylonia yang pernah ditemukan adalah sebuah tablet yang dikenal dengan nama Plimpton 322. Tablet ini bernomor katalog 322 di koleksi G.A. Plimpton di Universitas Columbia. Plimpton 322 ditulis oleh orang Babylonia sekitar tahun 1900 sampai 1600 SM, dan pertama kali dideskripsikan oleh Neugebauer dan Sachs pada tahun 1945.
- 12.
- 13. Sejarah Mesir kuno PeradabanMesir kuno yang berlangsung selama kurang lebih 2500 tahun telah meninggalkan banyak peninggalan serta memberikan inspirasi bagi penemuan-penemuan berikutnya yaitu mulai konsep geometri dengan teknik pembangunan monumen seperti piramida, kuil, dan obelisk, serta pengetahuan matematika berupa prinsip-prinsip yang mendasari teorema Pythagoras.
- 14. Penemuan – PenemuanMesir Kuno 1. Mesir kuno menggunakan sistem bilangan basis 10 Pada sekitar 3000 SM, orang Mesir memiliki sistem penulisan yang didasarkan pada Hieroglif. Dalam representasi baik sistem nomor selalu diberikan dalam basis 10. Dengan ini berarti bahwa mereka memiliki simbol terpisah untuk satuan, puluhan, ratusan, ribuan, puluhribuan, ratusribuan, dan jutaan.
- 15. Berikut ini adalahangka Hieroglif :
- 16. Misalnya untuk membuatbilangan 276, ada lima belas simbol yang diperlukan: dua simbol “ratusan”, tujuh simbol “puluhan”, dan enam simbol “satuan”. Bilangan tersebut di perlihatkan sebagai berikut :
- 17. • Kebanyakan peninggalannaskah matematika Mesir Kuno berupa papirus. Salah satunya Papirus Rhind. • Lembaran rhind memberikan rumus-rumus luas dan cara-cara perkalian, pembagian, dan pengerjaan pecahan. Lembaran itu juga menjadi bukti bagi pengetahuan matematika lainnya termasuk bilangan komposit dan prima, rata-rata aritmetika, geometri, dan harmonic, dan pemahaman sederhana Saringan Eratosthenes dan teori bilangan sempurna yaitu bilangan 6. 2. Papirus Rhind
- 18. a) Penjumlahan padasistem bilangan mesir 3. Mesir kuno menggunakan operasi matematika dasar.
- 19. b) Perkalian padasistem bilangan Mesir Perkalian dalam sistem bilangan mesir dikerjakan dari pengulangan pelipatgandaan bilangan dengan unsur pengalinya kemudian menjumlahkannya. c) Pembagian pada sistem bilangan Mesir
- 20. Pecahan untuk orangMesir kuno terbatas pada pecahan tunggal (kecuali 2/3 dan 3/4). Sebuah pecahan tunggal adalah bentuk 1/n dimana n adalah bilangan bulat dan ini diwakili dalam angka hieroglif dengan menempatkan simbol yang mewakili sebuah “mulut”, yang berarti “bagian”, di atas nomor tersebut. 4. Mesir Kuno mengenal pecahan
- 21. Berikut ini gambarpecahan pada zaman Mesir Kuno:
- 22. Berikut adalah beberapacontoh: Perhatikan bahwa ketika bilangan yang mengandung terlalu banyak simbol “bagian”, ditempatkan di atas bilangan bulat, seperti dalam 1/249, maka simbol “bagian” ditempatkan di atas “bagian pertama” bilangan. Simbol diletakkan di atas bagian pertama karena bilangan ini dibaca dari kanan ke kiri.
- 24. 5. Mesir Kunomengenal angka Hieratic pada zaman Kerajaan Baru – sekitar 1600 SM sampai 1000 SM. Sistem bilangan lain yang digunakan orang Mesir setelah penemuan tulisan di papirus, terdiri dari angka Hieratic. Angka ini memungkinkan bilangan ditulis dalam bentuk yang jauh lebih rapi dari sebelumnya saat menggunakan sistem yang membutuhkan lebih banyak simbol yang harus dihafal.
- 25. Berikut adalah versidari angka Hieratic :
- 26. Berikut ini adalahsalah satu cara orang Mesir menulis 2765 dalam angka Hieratic. Berikut ini adalah cara kedua menulis 2765 dalam angka Hieratic dengan urutan terbalik.
- 28. 7. Mesir mengenalnaskah yang berisikan soal kata atau soal cerita . Naskah matematika Mesir pada zaman Kerajaan Pertengahan pada 1890 SM adalah lembaran Moskwa. Naskah ini berisikan soal kata atau soal cerita, yang barangkali ditujukan sebagai hiburan . Naskah matematika Mesir pada zaman Kerajaan Pertengahan pada 1890 SM adalah lembaran Moskwa. Naskah ini berisikan soal kata atau soal cerita, yang barangkali ditujukan sebagai hiburan
- 29. Soal ini memberikanmetoda untuk memperoleh volume limas terpenggal: “Jika diberikan: Limas terpenggal setinggi 6 satuan panjang, yakni 4 satuan panjang di bawah dan 2 satuan panjang di atas. Anda menguadratkan 4, sama dengan 16. Anda menduakalilipatkan 4, sama dengan 8. Anda menguadratkan 2, sama dengan 4. Anda menjumlahkan 16, 8, dan 4, sama dengan 28. Anda ambil sepertiga dari 6, sama dengan 2. Anda ambil dua kali lipat dari 28, sama dengan 56. Maka lihatlah, hasilnya sama dengan 56. Anda memperoleh kebenaran.” Contoh soal cerita :
- 31. Mesir mengenal Phytagoras Dari pengamatan Pythagorasmelihat orang-orang Mesir menggunakan mistar dan tali pembanding untuk menghitung tinggi bangunan maka ia terinspirasi untuk membuat hukum matematika untuk menghitung tinggi dan sisi miring segitiga siku- siku. Mesir kuno telah memulai perhitungan tentang unsur-unsur segitiga dan menemukan segitiga keramat dengan sisi-sisi 3, 4 dan 5.
- 32. Geometri Mesir Pada MasaMesir Kuno penggunaan Matematika khususnya Geometri hanya digunakan secara praktis. Pada saat itu geometri hanya digunakan untuk keperluan yang sangat mendasar yaitu pemantauan ukuran tanah milik penduduk untuk keperluan pemungutan pajak. untuk menentukan luas-luas dan volume-volume dari berbagai bangun datar dan bangun ruang merupakan hasil dari trial and error, mereka mendasari perhitungannya dari sebuah fakta tanpa harus membuktikan secara deduktif.
- 34. Contoh Soal MesirKuno 1) Aritmatika Mesir Kuno •Mengalikan Hitunglah perkalian 22 dengan 26 ? Penyelesaian: Karena 22 = 16 + 4 + 2, maka : 1 26 2* 52* 4* 104* 8 208 16* 416* 22=2+4+16 572=52+104+416 Sehingga didapat bahwa 22 x 26 = 572
- 38.
- 39.
- 40. Tokoh-Tokoh Matematika Mesir Kuno Thales(624-546 SM) Phytagoras (582 SM – 496 SM) Eudoxus (408 – 355 SM)Euclid (330 - 275 SM) Archimedes (287 - 212 SM) Eratosthenes (276 SM - 194 SM)
- 41. Thales (624-546 SM)Thales(624-546 SM) Lahir di kota Miletos. Thales adalah seorang saudagar yang sering berlayar ke Mesir. Thales adalah seorang filsuf yang mengawali sejarah filsafat Barat pada abad ke-6 SM. Thales juga dikenal sebagai ahli geometri, astronomi, dan politik. Thales adalah orang yang pertama kali memikirkan tentang asal mula terjadinya alam semesta.
- 42. Phytagoras (582 SM– 496 SM) • Lahir di pulau Samos, di daerah Ionia. • Perjalanan Phytagoras ke Mesir merupakan salah satu bentuk usahanya untuk berguru, menimba ilmu, pada imam- imam di Mesir. • Pythagoras dan murid-muridnya percaya bahwa segala sesuatu di dunia ini berhubungan dengan matematika.
- 43. Eudoxus (408 –355 SM) Eudoxus adalah anak Arsghnes, dia lahir di Cnidus, Asia kecil (sekarang Turki). Pergi ke Tarentum, Italia untuk belajar pada Archytas. Pergi ke Sisilia, dan belajar obat-obatan pada Philiston. 2 bulan di Athena untuk mengikuti kuliah Plato dan filsuf-filsuf lain pada akademi Plato. Beberapa tahun di Mesir untuk belajar astronomi pada pendeta-pendeta Heliopolis. Menciptakan teori tentang planet, yang sangat terkenal dan diterbitkan dalam buku On Velocities. Membuat definisi tentang prakiraan panjang suatu bilangan irrasional dengan methode perkalian silang (cross multiplying) Eudoxus adalah anak Arsghnes, dia lahir di Cnidus, Asia kecil (sekarang Turki). Pergi ke Tarentum, Italia untuk belajar pada Archytas. Pergi ke Sisilia, dan belajar obat-obatan pada Philiston. 2 bulan di Athena untuk mengikuti kuliah Plato dan filsuf-filsuf lain pada akademi Plato. Beberapa tahun di Mesir untuk belajar astronomi pada pendeta-pendeta Heliopolis. Menciptakan teori tentang planet, yang sangat terkenal dan diterbitkan dalam buku On Velocities. Membuat definisi tentang prakiraan panjang suatu bilangan irrasional dengan methode perkalian silang (cross multiplying)
- 44. Euclid (330 -275 SM) • Theorema-theorema baru pada masa Euclid: kurva-kurva, lingkaran-lingkaran dan bentuk- bentuk lain dipelajari sama halnya seperti garis lurus dan bidang–bidang datar. • Euclid belajar pada akademi Plato. • Pada masa tuanya, Euclid pindah untuk mengajar di Alexandria • Ia lebih suka matematika untuk dipelajari bukan untuk aplikasi. • Euclid meninggal di Alexandria.
- 45. • Lahir diKyrene (Libya modern). • Semasa muda, dia pindah ke Aleksandria, Mesir. • Pada tahun 23 SM, dia menjadi kepala perpustakaan di Perpustakaan Besar Alexandria. • Ia dicatat oleh Cleomedes dalam On the Circular Motions of the Celestial Bodies sebagai orang yang telah menghitung keliling Bumi pada sekitar tahun 240 SM. • Karya lain dari Eratosthenes adalah saringan Eratosthenes sebagai cara menemukan bilangan prima. Eratosthenes (276 SM - 194 SM)
- 46. Archimedes (287 -212 SM) • Archimedes adalah seorang matematikawan, fisikawan, astronom sekaligus filusuf. • Archimedes dilahirkan di kota pelabuhan bernama Syracuse, kota ini sekarang dikenal sebagai Sisilia. • Archimedes dikenal dengan teorinya tentang hubungan antara permukaan dan volume dari sebuah bola terhadap silinder, teori dan rumus dari prinsip hydrostatic dan peralatan untuk menaikkan air ‘Archimedes Screw’ atau Sekrup Archimedes. • Nama Archimedes menjadi terkenal setelah ia melompat dari bak mandinya dan berlari-lari telanjang setelah membuktikan bahwa mahkota raja tidak terbuat dari emas murni. • Ia mendefinisikan perbandingan antara keliling lingkaran dan jari-jari lingkaran yang dikenal sebagai pi sebesar 3.1429. • Saat tewas Archimedes sedang mengerjakan persoalan geometri dengan menggambarkan lingkaran-lingkaran di atas tanah
- 47.
- 48. 0 20 40 60 80 100 120 140 160 180 1st Qtr 2ndQtr 3rd Qtr 4th Qtr South North East PowerPoint chart object
- 49. SEJARAHMATEMATIKA “SISTEMNUMERASI” Mengingat keterbatasan sumberliteratur, makauntuk keakuratan datasejarah yang diperoleh, disarankan kepadapembacajuga memiliki sumber literatur lain yang lebih valid, di luar sumber bacaan dari internet yang belum dapat divalidasi seluruhnya. Kelompok : II(DUA) 4-DMatematika
- 50. Example use • Bulletpoints are like this • Text and lines are like this – Hyperlinks like this – Visited hyperlinks like this Table Text box
- 51.
- 52. Use of templates Youare free to use these templates for your personal and business presentations. Do Use these templates for your presentations Display your presentation on a web site provided that it is not for the purpose of downloading the template. If you like these templates, we would always appreciate a link back to our website. Many thanks. Don’t Resell or distribute these templates Put these templates on a website for download. This includes uploading them onto file sharing networks like Slideshare, Myspace, Facebook, bit torrent etc Pass off any of our created content as your own work You can find many more free templates on the Presentation Magazine website www.presentationmagazine.com We have put a lot of work into developing all these templates and retain the copyright in them. They are not Open Source templates. You can use them freely providing that you do not redistribute or sell them.