What is physics

What is Physics?
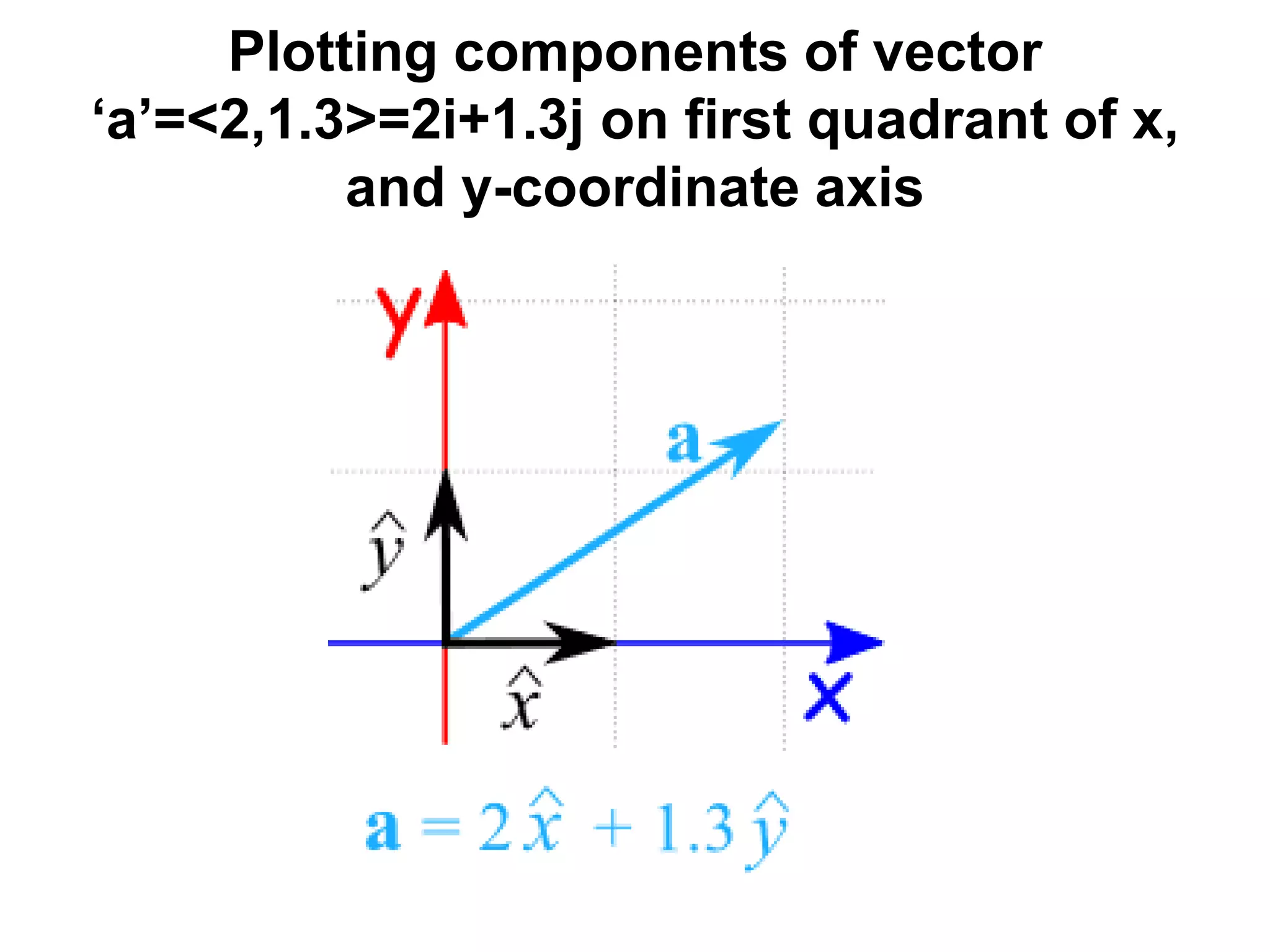
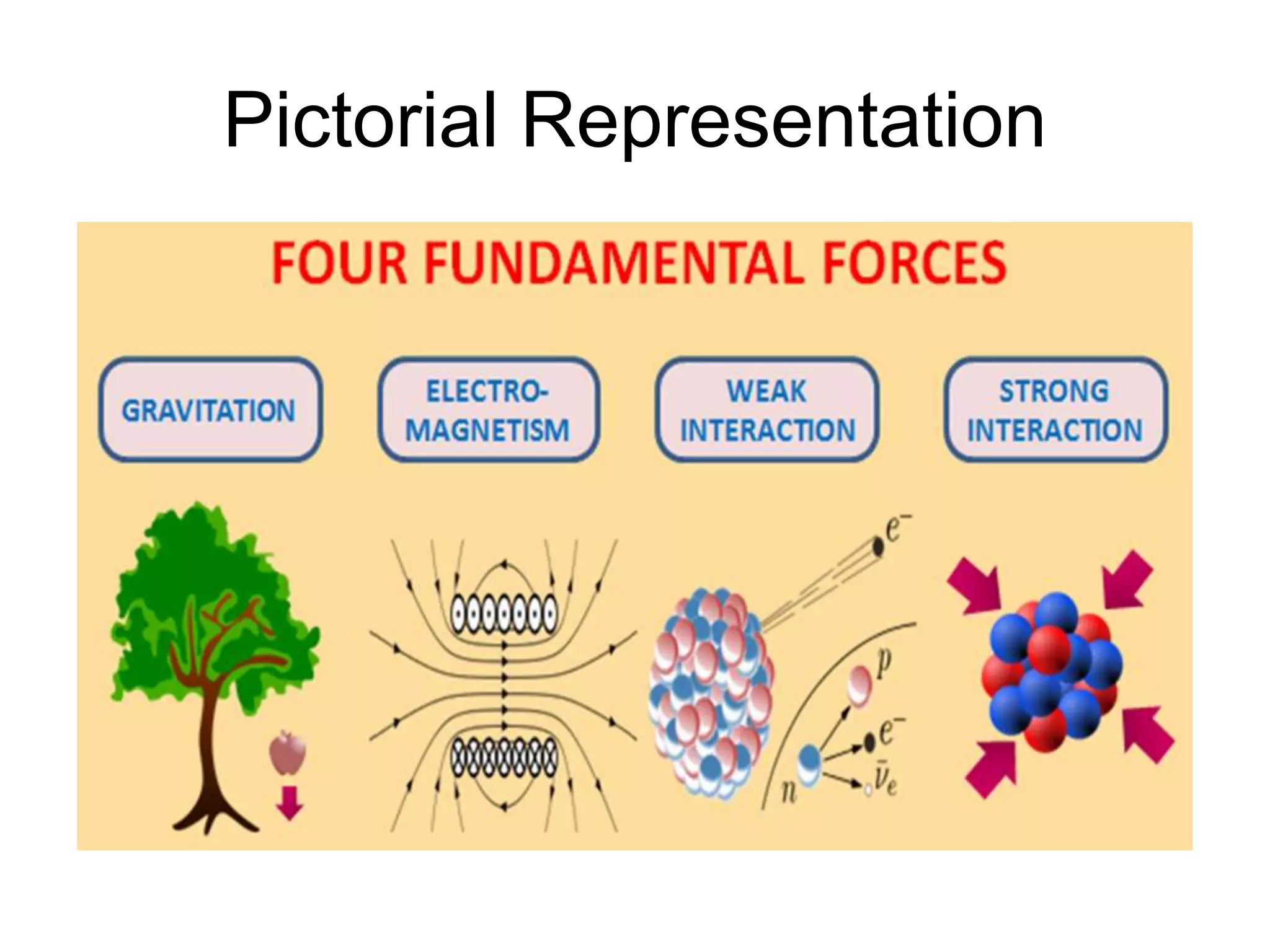
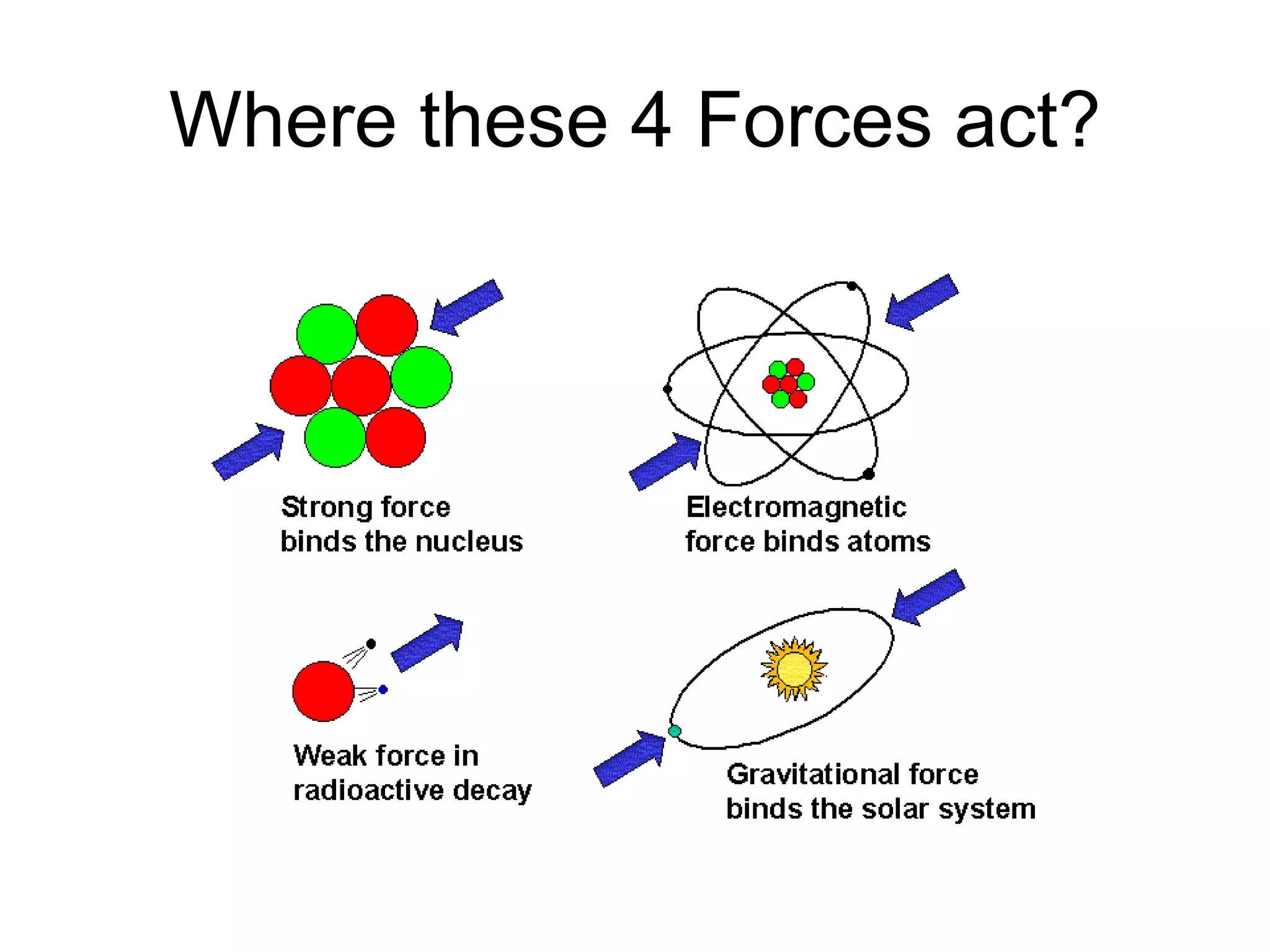
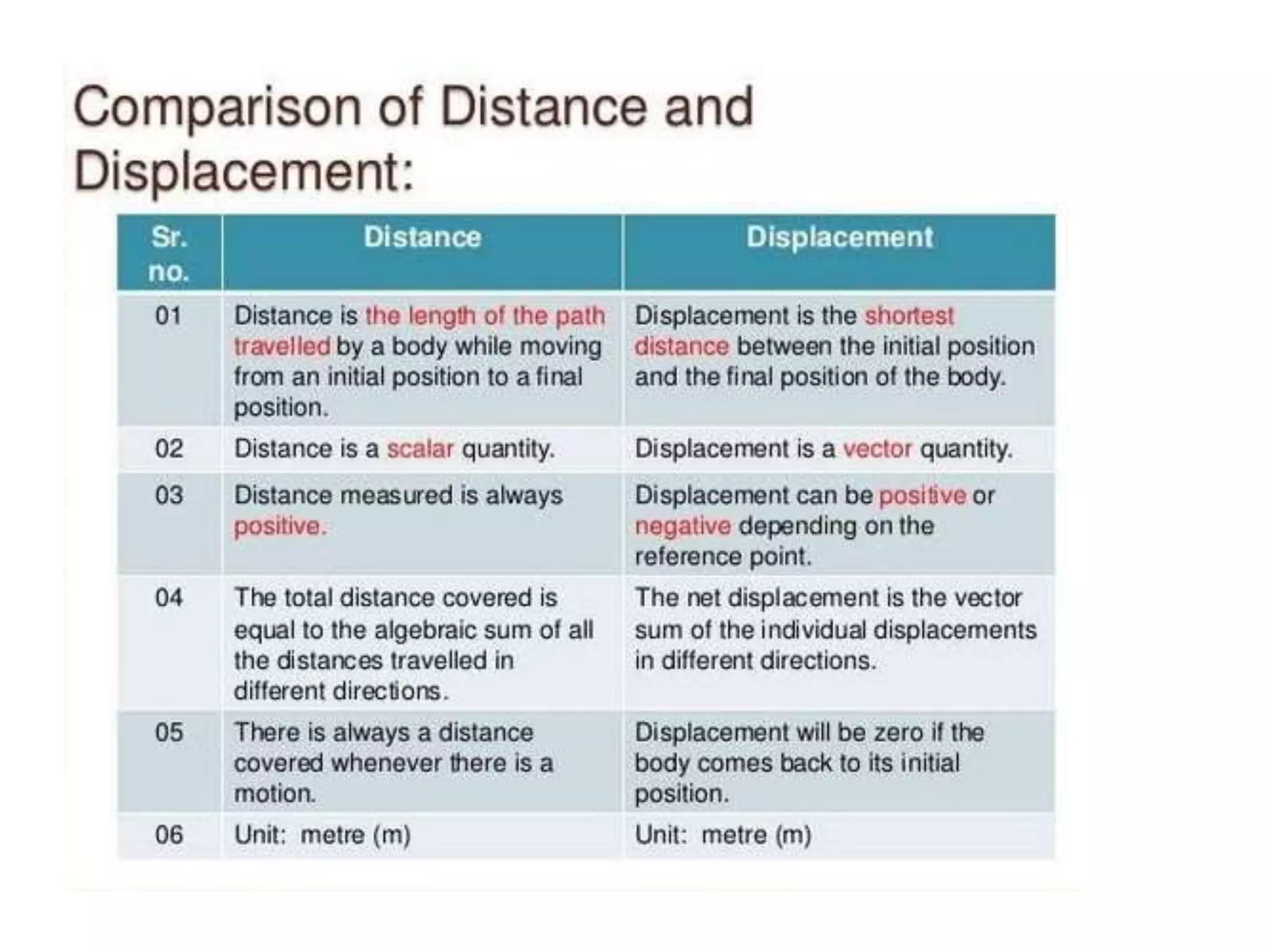
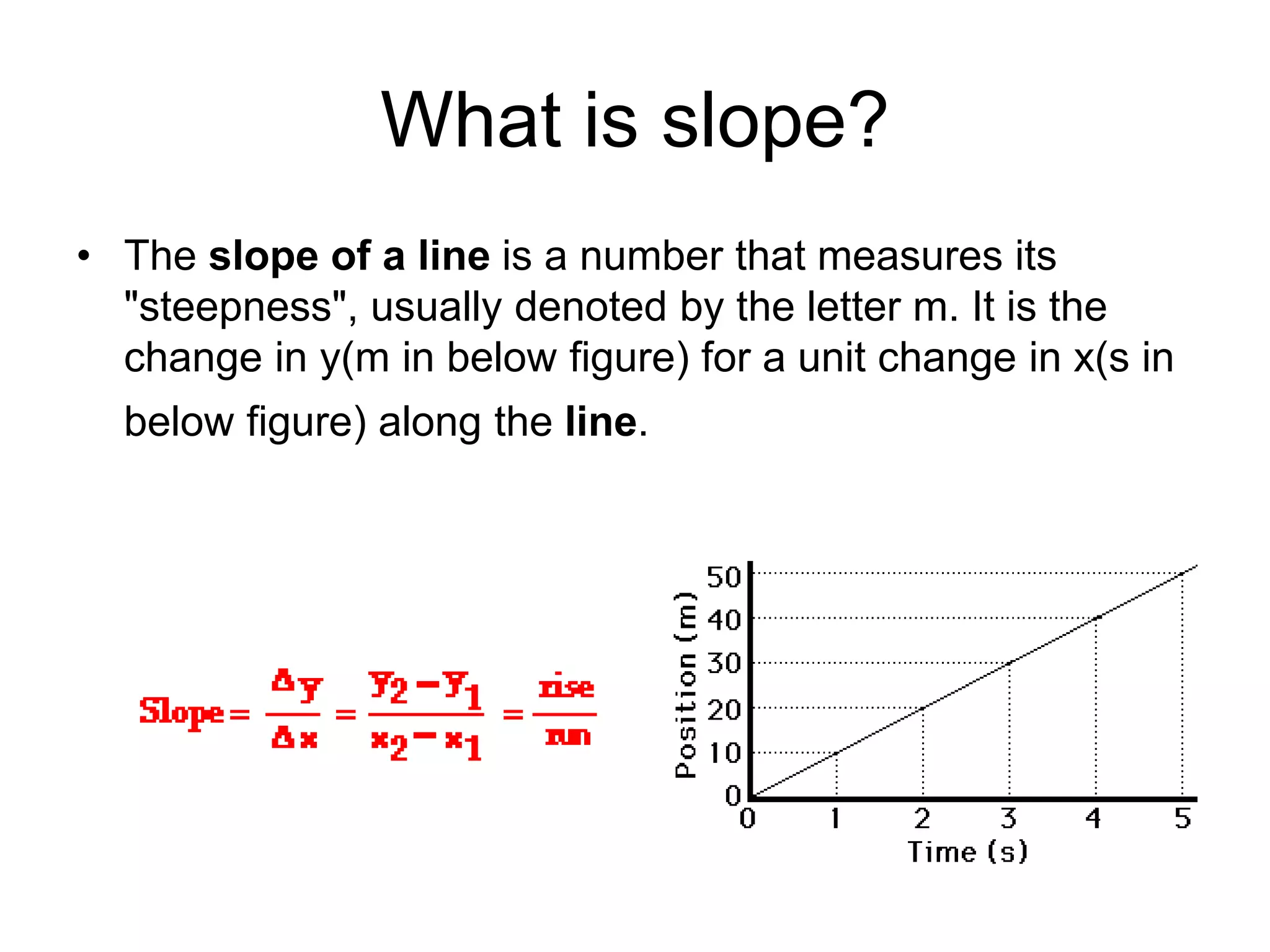
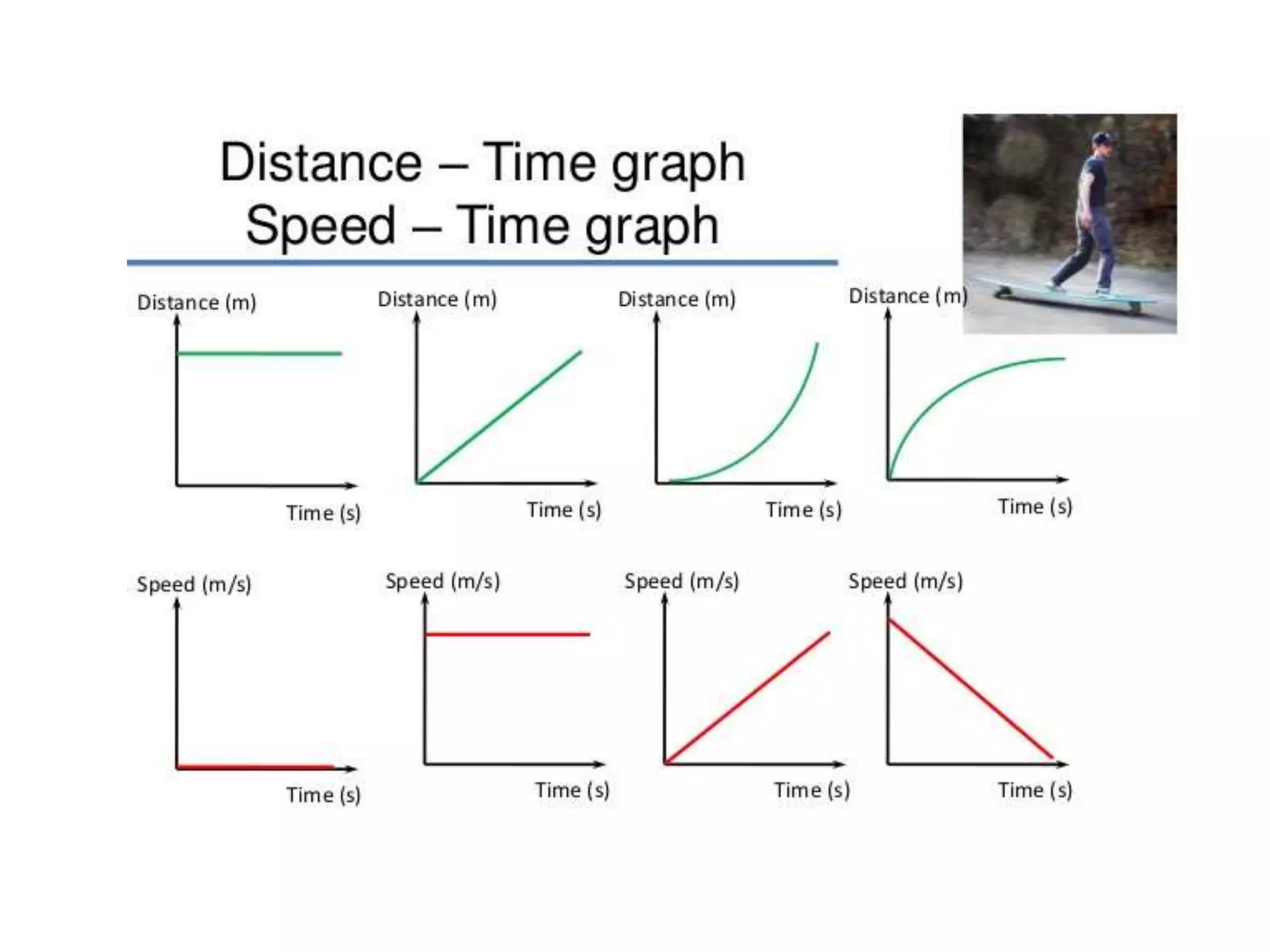
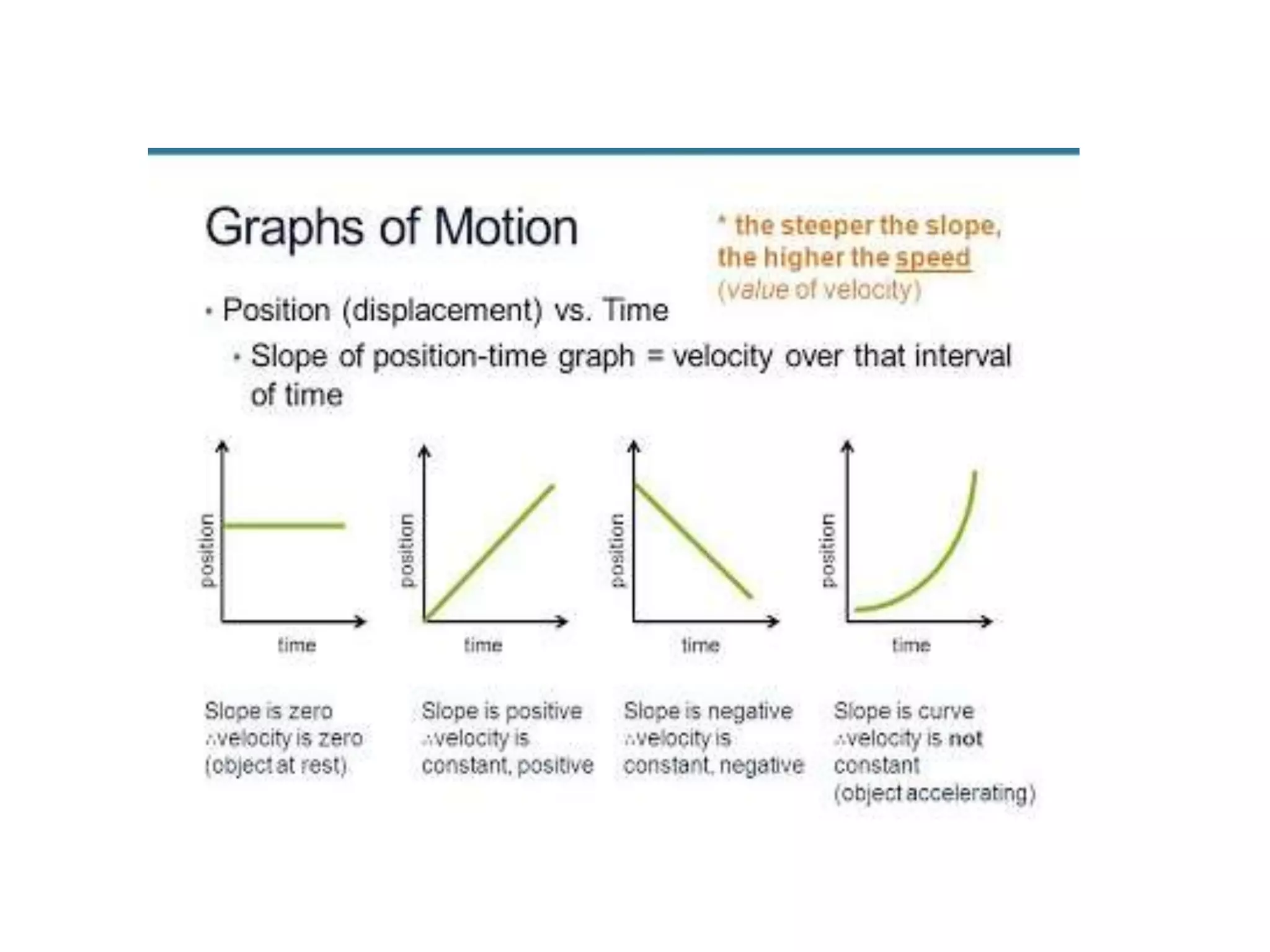
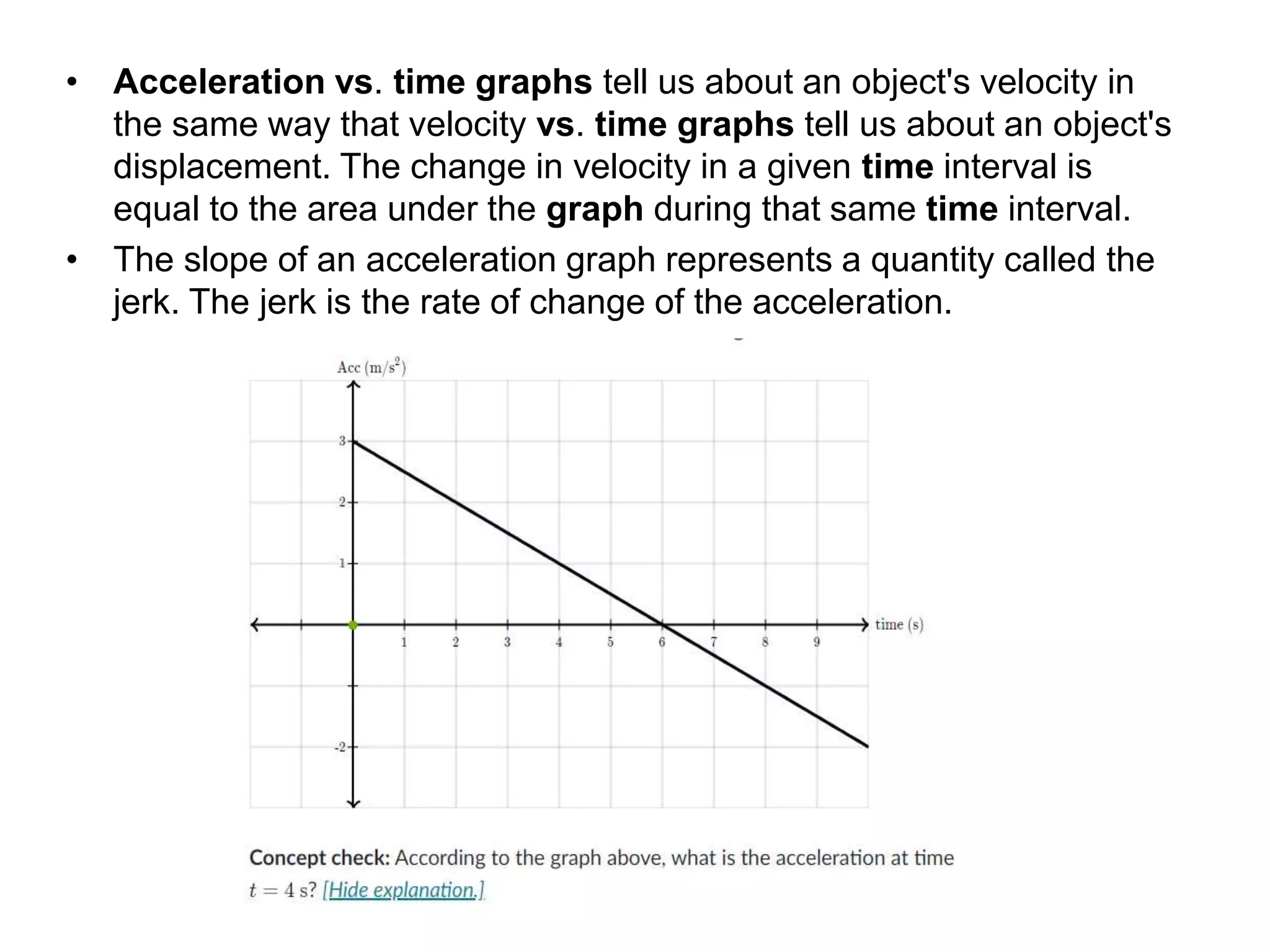
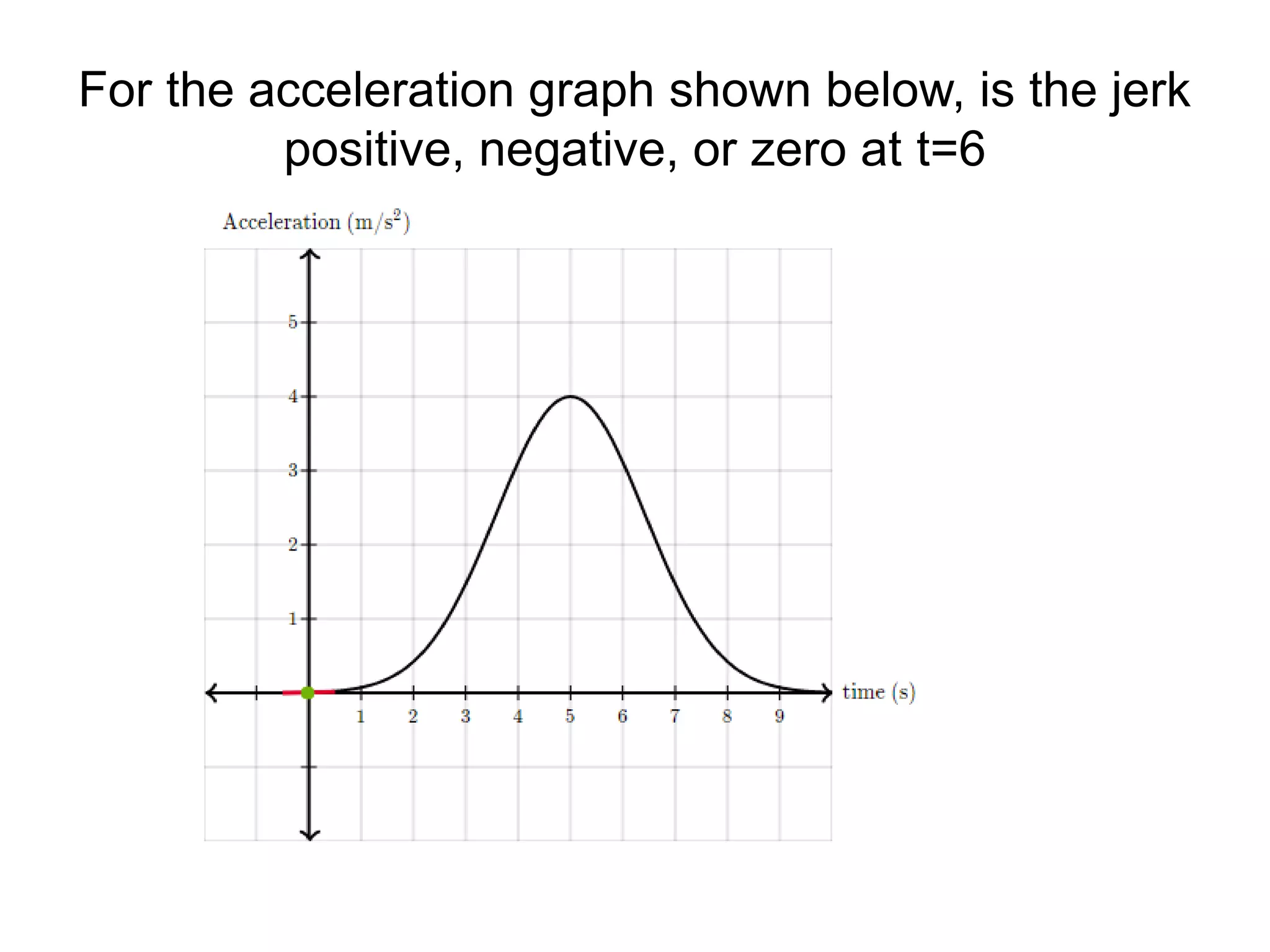
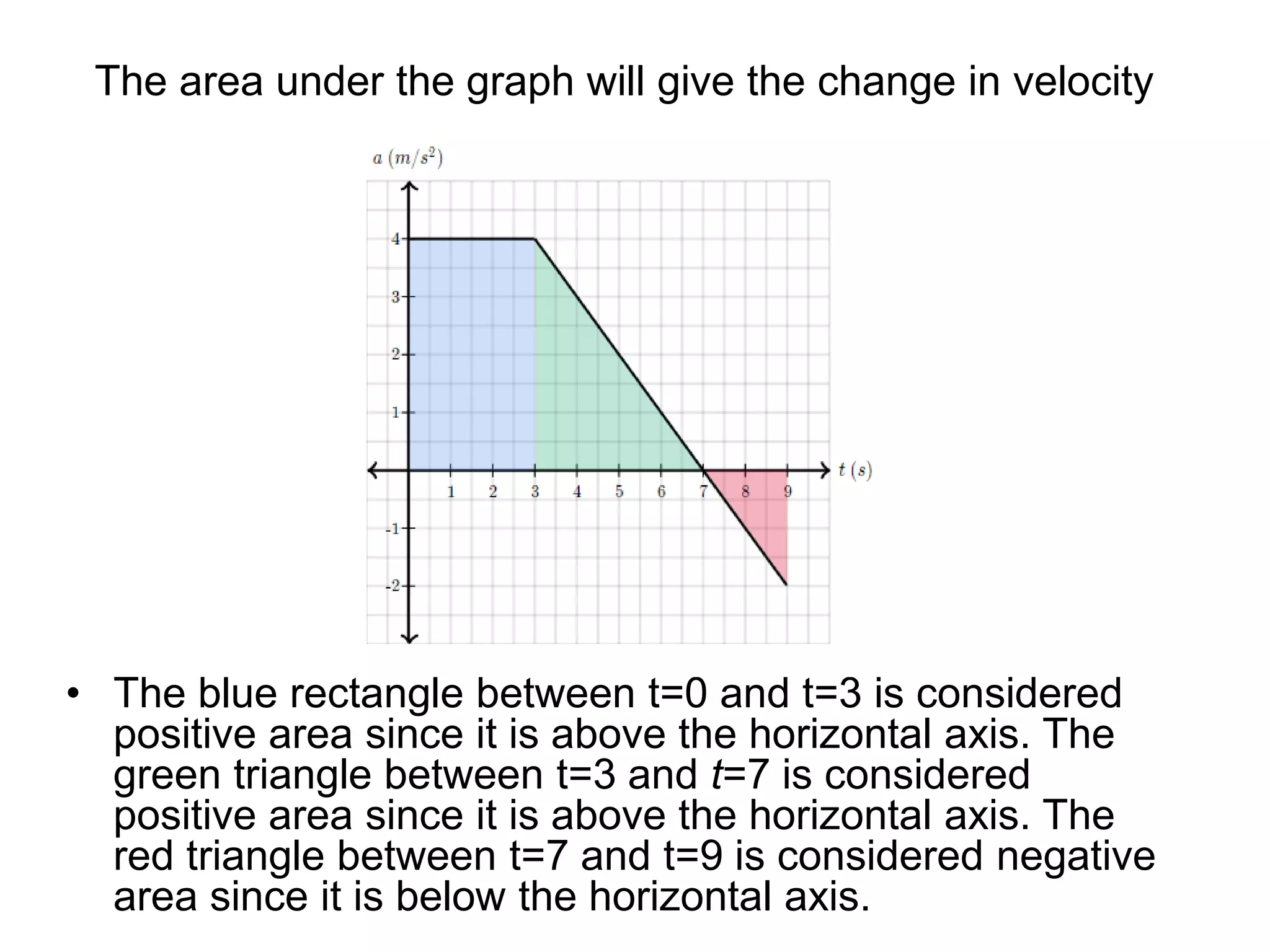
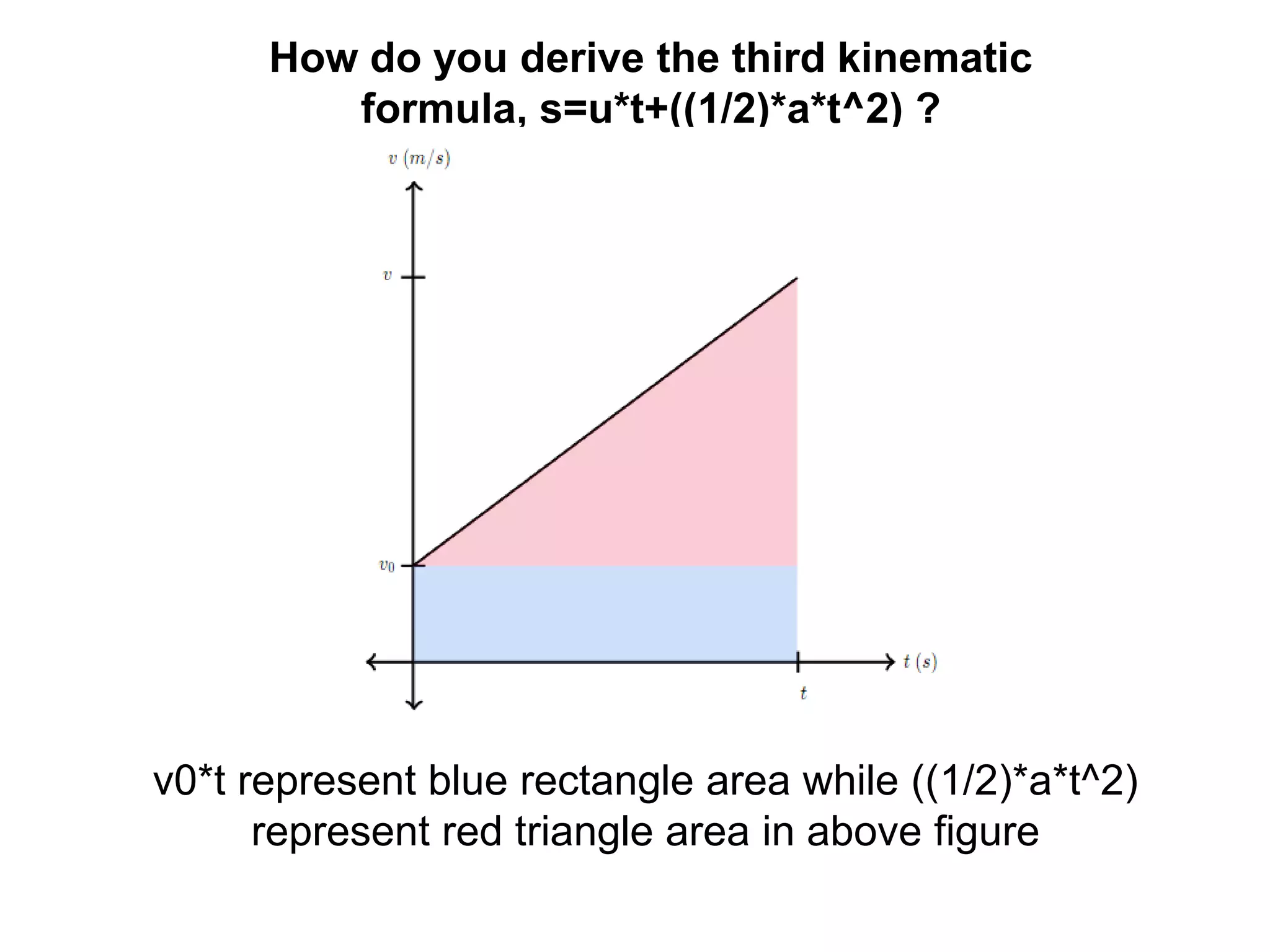
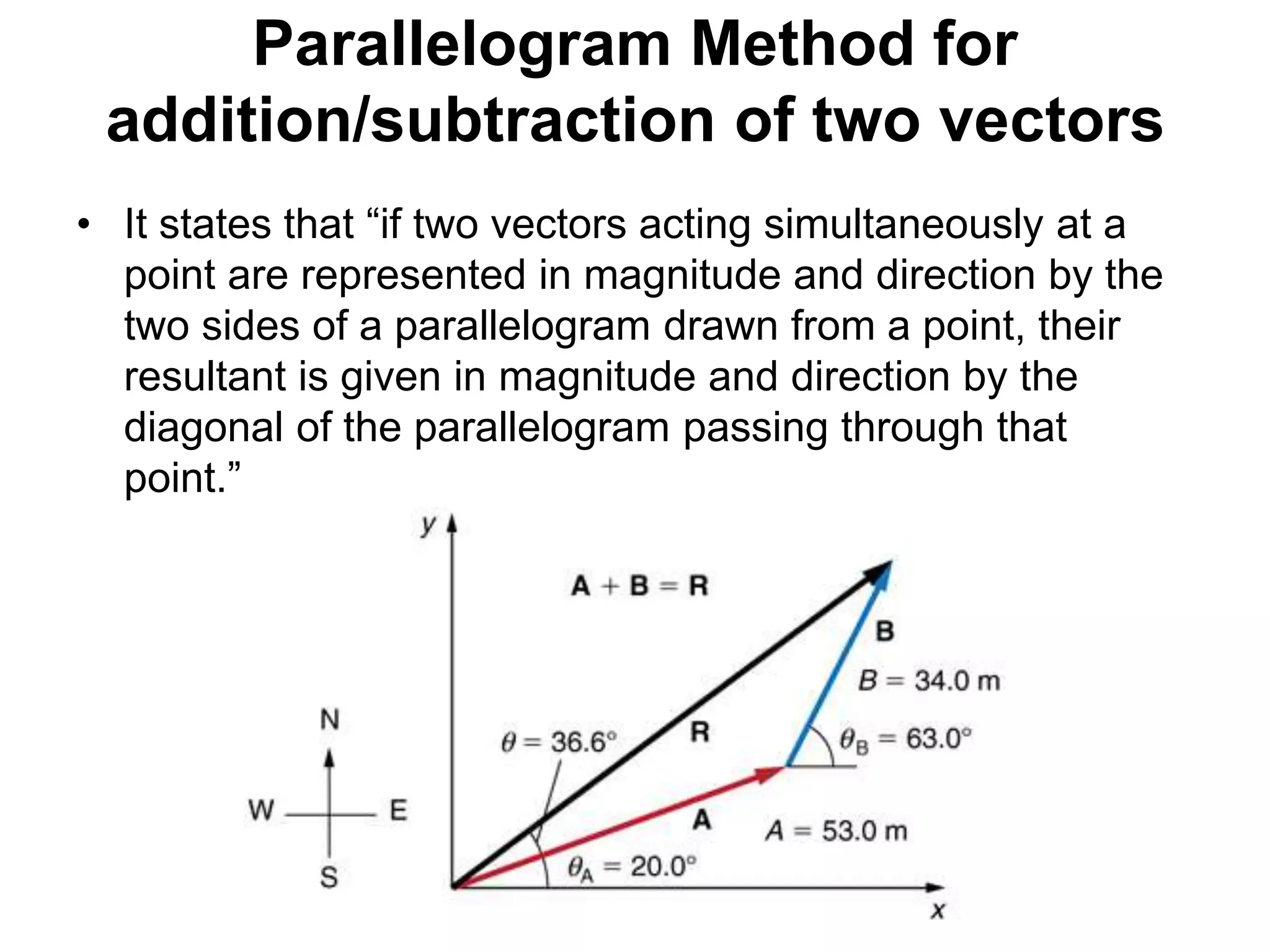
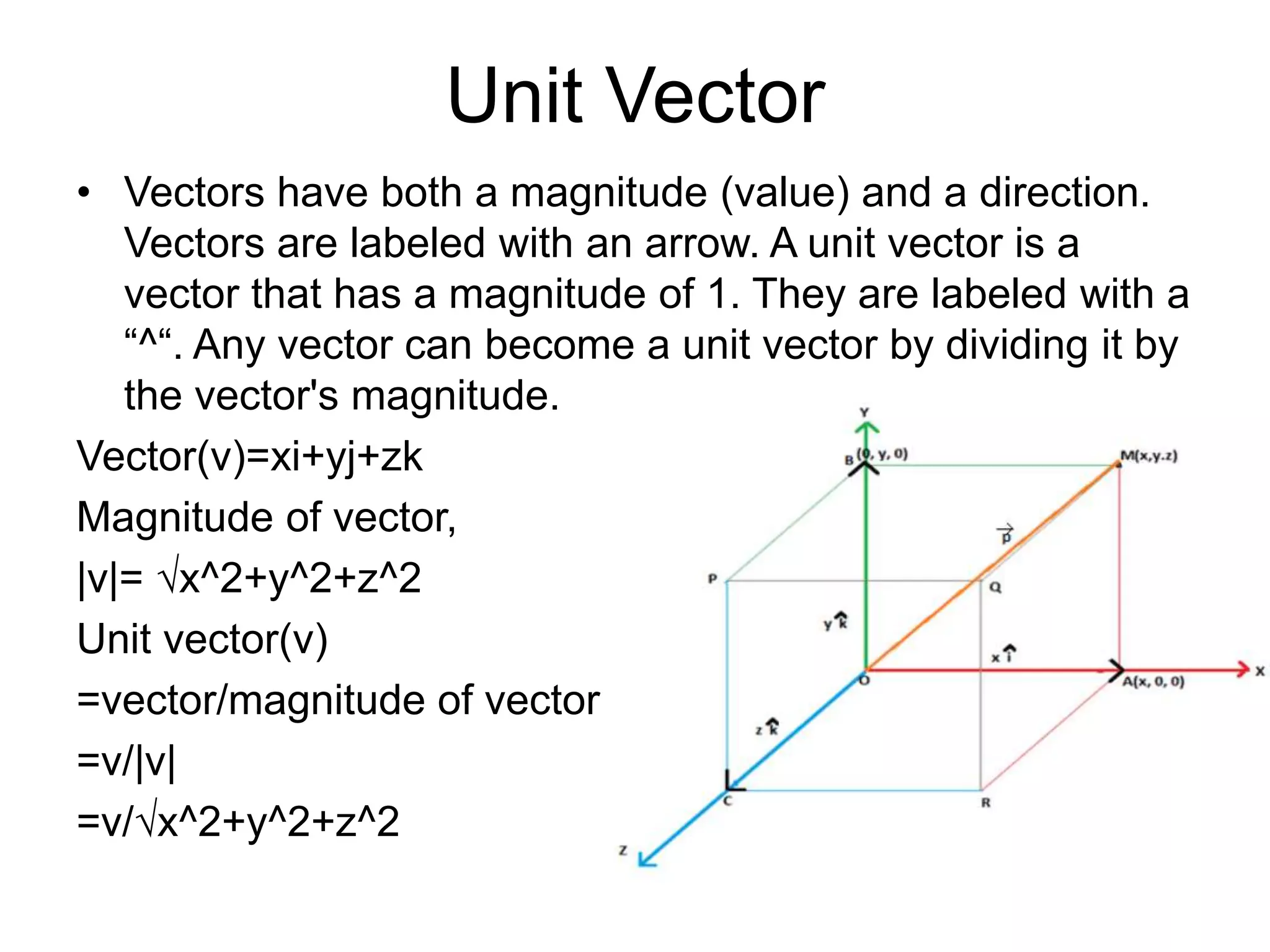
Physics is the branch of science
concerned with the nature and properties
of matter and energy in space and time.
And How they are related to each other.
The subject matter of physics includes
mechanics, heat, light and other radiation,
sound, electricity, magnetism, and the
structure of atoms.

Four Fundamental Forces of Physics with their
magnitudes and Ranges
1) Gravitational force: Weakest Force but has infinite
Range
2) Weak Nuclear force: Next Weakest Force but short
range
3) Electromagnetic force: Stronger Force with infinite
range
4) Strong Nuclear force: Strongest Force, but Short
Range

Unit and Measurements?
• Word unit as used in physics refers to the
standard measure of a quantity. Some
fundamental quantities and their
respective units are: time —- second. mass —-
kilogram. length —- meter.
• The SI system, also called the metric system, is
used around the world.
• There are seven basic units in the SI system: the
meter (m), the kilogram (kg), the second (s), the
kelvin (K), the ampere (A), the mole (mol), and
the candela (cd).

Measurement
• Measurement is defined as the act
of measuring or the size of something.
• (or) To measure something is to give a number
to some properties of the thing.
• Measurement can be written using many
different units.
• there are two main systems of measurement in
the world: the SI or Metric (or decimal) system
and the US standard system

Motions in Straight Line
• Distance, displacement, and coordinate systems: Motion
in a straight line
• Average velocity and average speed: Motion in a straight
line
• Velocity and speed from graphs: Motion in a straight line
• Acceleration: Motion in a straight line
• Kinematic formulas: Motion in a straight line
• Objects in freefall: Motion in a straight line
• Rectilinear motion (integral calc): Motion in a straight line
• Relative velocity in 1D: Motion in a straight line

What are Scalar and vector
Quantity
• In physics, a physical quantity is any physical property that can be
quantified, that is, can be measured using numbers.

What are Distance and
Displacement?

What is slope?
• The slope of a line is a number that measures its
"steepness", usually denoted by the letter m. It is the
change in y(m in below figure) for a unit change in x(s in
below figure) along the line.

How are Distance and Speed
related?
• Distance is an amount of space (e.g., that
has been traversed by an object, between
two bodies, or the like).
• Speed is the rate of change of distance;
mathematically, speed is the time
derivative of distance.

Average Speed versus Average
Velocity
• The average speed is the distance (a scalar quantity)
per time ratio. Speed is ignorant of direction. On the
other hand, velocity is a vector quantity; it is direction-
aware. Velocity is the rate at which the position
changes.

Ques) In travelling from Pune to Nagpur ,Rahul drove
his bike for 2 hours at 60 kmph and 3 hours at 70
kmph.
• Sol 1) We know that, Distance = Speed × Time
So, in 2 hours, distance covered = 2 × 60 = 120
km
in the next 3 hours, distance covered = 3 × 70 =
210 km
Total distance covered = 120 + 210 = 330 km
Total time = 2 + 3 = 5 hrs
Avg. Speed = TotaldistancecoveredTimetaken
Avg. Speed = 330/5 = 66 kmph

Ques) A person walks 4 meters east in 1 second,
then walks 3 meters north in 1 second. Determine
average speed and average velocity.
Solution
• Distance = 4 meters + 3 meters = 7 meters
• Displacement = = meters, to northeast.
• Time elapsed = 1 second + 1 second = 2 seconds.
• Average speed = distance / time elapsed = 7 meters / 2 seconds =
3.5 meters/second
• Average velocity = displacement / time elapsed = 5 meters / 2
seconds = 2.5 meters/second

Ques) A runner travels around rectangle track with length =
50 meters and width = 20 meters. After travels around
rectangle track two times, runner back to starting point. If
time elapsed = 100 seconds, determine average speed and
average velocity.
• Solution
• Circumference of rectangle = 2(50 meters) + 2(20
meters) = 100 meters + 40 meters = 140 meters.
• Travels around rectangle 2 times = 2(140 meters) = 280
meters.
• Distance = 280 meter.
• Displacement = 0 meter. (runner back to start point)
• Average speed = distance / time elapsed = 280 meters /
100 seconds = 2.8 meters/second.
• Average velocity = displacement / time elapsed = 0 / 100
seconds = 0.

Instantaneous velocity versus
Instantaneous speed
• Instantaneous velocity. ... Suppose
the velocity of the car is varying, because
for example, you're in a traffic jam. You look at
the speedometer and it's varying a lot, all the
way from zero to 60 mph.
• Instantaneous velocity is the velocity at a
specific instant in time. This can be different to
the average velocity if the velocity isn't
constant. ... Instantaneous velocity is a
vector. Instantaneous speed is the magnitude
of instantaneous velocity. It has the same
value but is not a vector so it has no direction.

Velocity(at t=0)=dx/dt(at t=0)=slope
of tangent at time=t0

What is Acceleration?
• In physics or physical science, acceleration (symbol: a)
is defined as the rate of change (or derivative with
respect to time) of velocity. ... To accelerate an object is
to change its velocity, which is accomplished by altering
either its speed or direction (like in case of uniform
circular motion) in relation to time.
• Examples. An object was moving north at 10 meters per
second. The object speeds up and now is moving north
at 15 meters per second. The object has accelerated.
• in terms of SI units, dividing the meter per second [m/s]
by the second [s].

A bike accelerates uniformly from rest to a speed of 7.10
m/s over a distance of 35.4 m. Determine the acceleration
of the bike.
• Given vi = 0 m/s, vf = 7.10 m/s, s = 35.4 m
• Find:a = ??
• vf^2 = vi^2 + 2*a*s
• (7.10 m/s)^2 = (0 m/s)^2 + 2*(a)*(35.4 m)
• 50.4 m^2/s^2 = (0 m/s)2 + (70.8 m)*a
• (50.4 m^2/s^2)/(70.8 m) = a
• a = 0.712 m/s^2

An engineer is designing the runway for an airport. Of the
planes that will use the airport, the lowest acceleration rate
is likely to be 3 m/s2. The takeoff speed for this plane will
be 65 m/s. Assuming this minimum acceleration, what is
the minimum allowed length for the runway?
• Given vi = 0 m/s, vf = 65 m/s, a = 3 m/s^2
Find: s = ??
• vf^2 = vi^2 + 2*a*s
• (65 m/s)^2 = (0 m/s)^2 + 2*(3 m/s2)*s
• 4225 m^2/s^2 = (0 m/s)^2 + (6 m/s^2)*s
• (4225 m2/s2)/(6 m/s2) = s
• s = 704 m

Velocity versus Time Graphs
velocity vs. time graphs tell us about an object's
displacement.
Object’s velocity increases for the first 4 seconds of the race, it remains
constant for the next 3 seconds, and it decreases during the last 3
seconds after she crosses the finish line.

w.r.t. x=u*t+((1/2)*a*t^2), v=u+a*t, v^2=u^2+2*a*x
What are velocity vs. time and acceleration vs.
time Graphs corresponding to position vs. time
Graph

• Acceleration vs. time graphs tell us about an object's velocity in
the same way that velocity vs. time graphs tell us about an object's
displacement. The change in velocity in a given time interval is
equal to the area under the graph during that same time interval.
• The slope of an acceleration graph represents a quantity called the
jerk. The jerk is the rate of change of the acceleration.

For the acceleration graph shown below, is the jerk
positive, negative, or zero at t=6

The area under the graph will give the change in velocity
• The blue rectangle between t=0 and t=3 is considered
positive area since it is above the horizontal axis. The
green triangle between t=3 and t=7 is considered
positive area since it is above the horizontal axis. The
red triangle between t=7 and t=9 is considered negative
area since it is below the horizontal axis.

What are 3 Kinematic Equations?
• 1st Equation: v=u+a*t
• 2nd Equation: s=u*t+((1/2)*a*t^2)
• 3rd Equation: v^2=u^2+(2*a*s)
• 4th Equation: v(avg)=(u+v)/2

How do you derive the first kinematic
formula, v=u+at ?
• We can start with the definition of
acceleration, a,:
• a=velocity difference/time difference
• a=(v-u)/t
• a*t=v-u
• a=u+a*t

An airplane lands with an initial velocity of 70.0 m/s and
then decelerates at 1.5m/s^2 for 40.0 s. What is its final
velocity?
• Solution
• 1. Identify the knowns. u=70m/s, a=-1.5m/s^, t=40s .
• 2. Identify the unknown. In this case, it is final velocity, v.
• 3. Determine which equation to use. We can calculate
the final velocity using the equation v=u+at.
• 4. Plug in the known values and solve.
• v=u+at=70m/s+(-1.5m/s^2)(40s)=10m/s

How do you derive the third kinematic
formula, s=u*t+((1/2)*a*t^2) ?
v0*t represent blue rectangle area while ((1/2)*a*t^2)
represent red triangle area in above figure

• So, displacement must be given by the total area under
the curve.

Ben Rushin is waiting at a stoplight. When it finally turns
green, Ben accelerated from rest at a rate of a 6.00
m/s^2 for a time of 4.10 seconds. Determine the
displacement of Ben's car during this time period.
• Given: a=6 m/s^2, t=4.2s
• Find s=??
Using equation s=u*t+((1/2)*a*t^2)
s = (0 m/s) • (4.1 s) + ½ • (6.00 m/s^2) • (4.10 s)^2
s = (0 m) + ½ • (6.00 m/s^2) • (16.81 s^2)
s = 0 m + 50.43 m
s = 50.4 m

How do you derive the third kinematic
formula, v^2=u^2+(2*a*s) ?
dv/ds=(dv/ds)*(dt/dt)
dv/ds=(dv/dt)*(dt/ds)=(a)*(1/v)=a/v

Ima Hurryin is approaching a stoplight moving with a
velocity of +30.0 m/s. The light turns yellow, and Ima
applies the brakes and skids to a stop. If Ima's acceleration
is -8.00 m/s^2, then determine the displacement of the car
during the skidding process.
• Given u=30m/s, a=-8m/s^2, v=0m/s
• Find s=??
Using equation v^2=u^2+(2*a*s)
(0 m/s)^2 = (30.0 m/s)^2 + 2 • (-8.00 m/s^2) • s
0 m^2/s^2 = 900 m^2/s^2 + (-16.0 m/s^2) • s
(16.0 m/s^2) • s = 900 m^2/s^2 - 0 m^2/s^2
(16.0 m/s^2)*s = 900 m^2/s^2
s = (900 m^2/s^2)/ (16.0 m/s^2)
s = (900 m^2/s^2)/ (16.0 m/s^2)
s = 56.3 m

Average velocity is displacement divided by time. Start with the formula
for displacement and divide it by t.
How do you derive the fourth kinematic
formula, v=(vi+vf)/2 ?

Ques) A truck is travelling forward at a constant velocity of
10.00 m/s, and then begins accelerating at a constant rate.
A short time later, the velocity of the truck is 30.00 m/s,
forward. What was the average velocity of the truck during
its acceleration?
• The initial velocity is vi = 10.00 m/s, in the forward
direction. The final velocity is vf = 30.00 m/s in the
forward direction. The average velocity during the
acceleration can be found using the formula:
v(avg)=(vi+vf)/2,
v(avg)=(10+30)/2
v(avg)=20 m/s
The average velocity during the truck's acceleration was
20.0 m/s, forward.

Ques) A child throws a ball in the air. The ball leaves her
hand with a velocity of 2.00 m/s upward. The ball
experiences acceleration due to gravity, and after a short
time, the velocity of the ball is 2.00 m/s downward. What is
the average velocity of the ball?
• Answer: If the positive direction is defined to be "up", then the initial
velocity vi = +2.00 m/s, and the final velocity vf = -2.00 m/s. The
average velocity of the ball can be found using these values and the
formula:
V(avg)=(vi+vf)/2
V(avg)=(2-2)/2
V(avg)=0
The average velocity of the ball within the time interval was 0.0 m/s.

• Average Velocity: to find the average velocity for a
given time interval, you would find the slope of the line
connecting those two points.
• Instantaneous Velocity: to find the instantaneous
velocity, you must find the slope of the line tangent to the
curve at that time
Average velocity & instantaneous
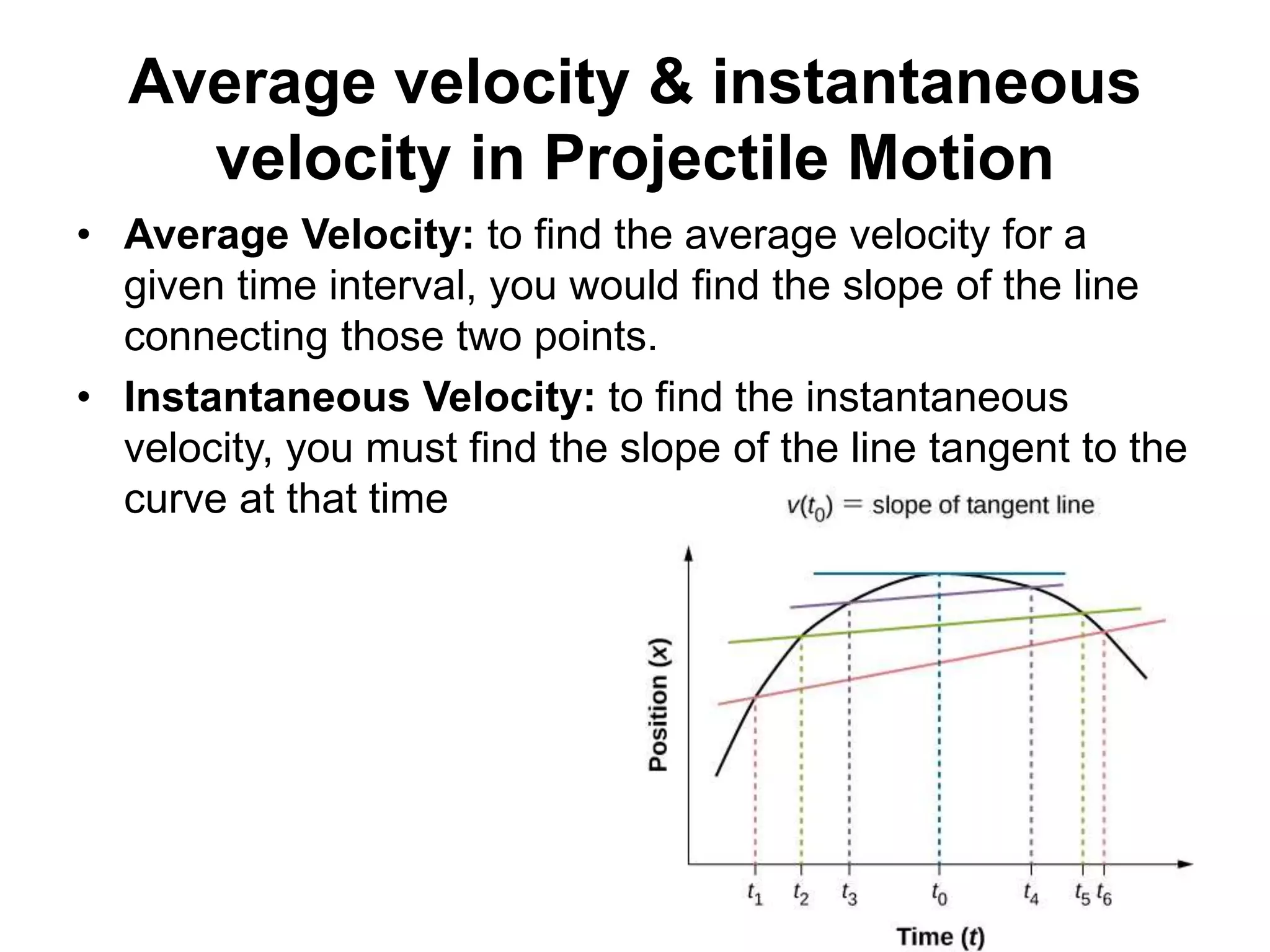
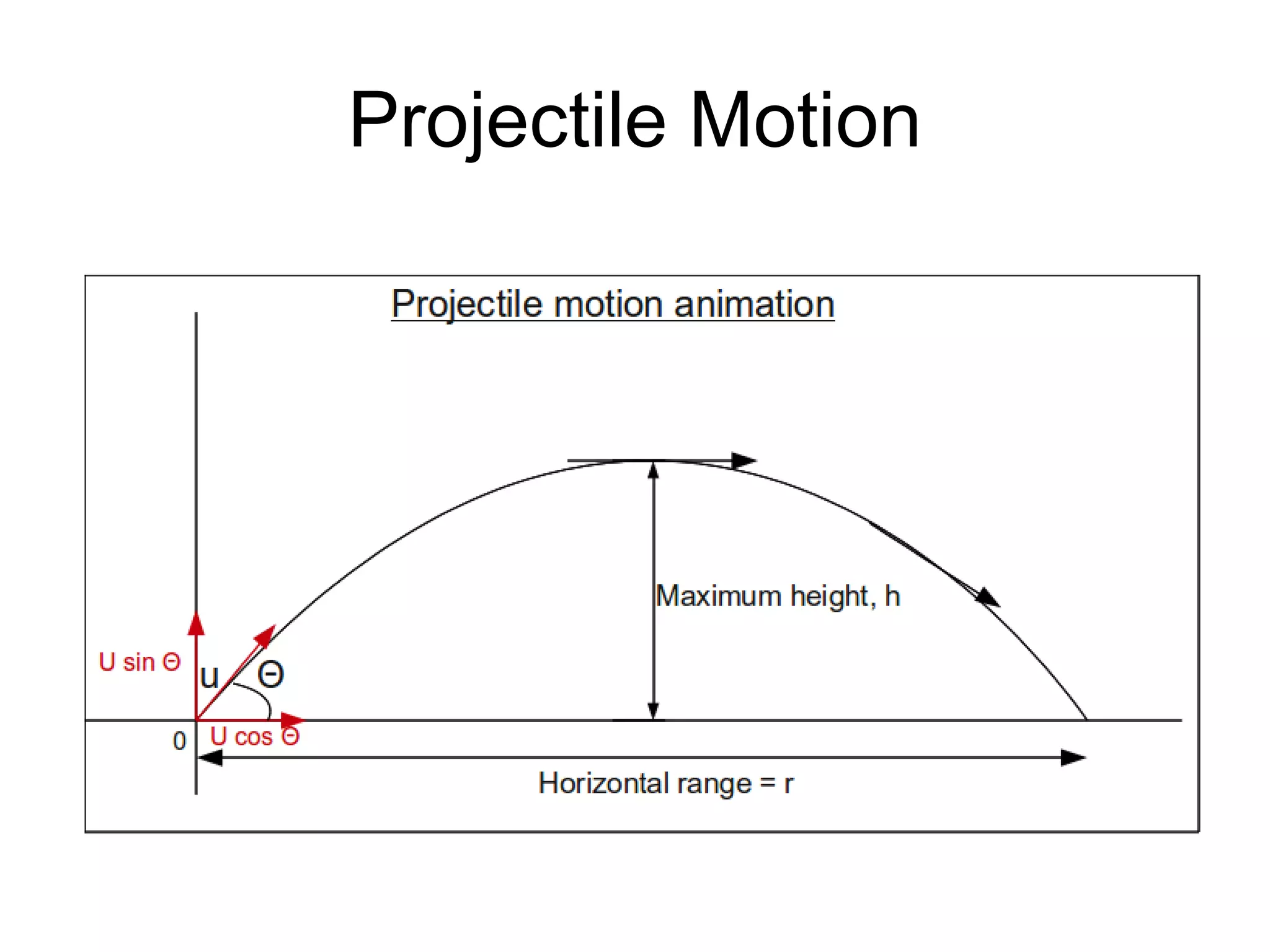
velocity in Projectile Motion

Projectile Motion (Parabolic
Trajectory) on ground
Projectile motion is a form of motion where an object moves in a
bilaterally symmetrical, parabolic path. The path that the object
follows is called its trajectory. Projectile motion only occurs when
there is one force applied at the beginning on the trajectory, after
which the only interference is from gravity.

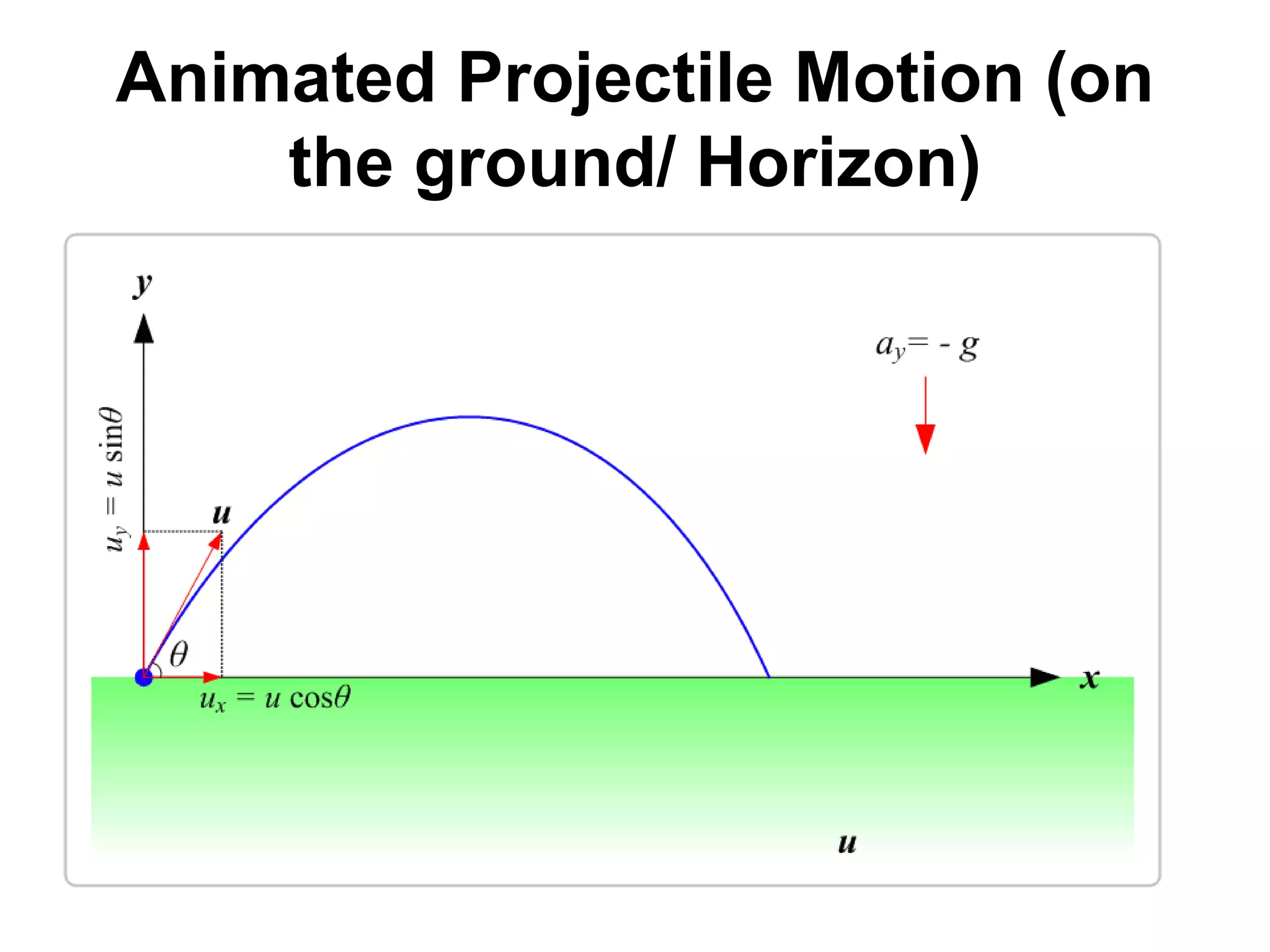
Animated Projectile Motion (on
the ground/ Horizon)

Time of Flight:
The time of flight of a projectile motion is the time from when the object
is projected to the time it reaches the surface.
As we discussed previously, T depends on the initial velocity
magnitude and the angle of the projectile:
T=2*ux/g =2*u* cosθ /g
Acceleration:
In projectile motion, there is no acceleration in the horizontal direction.
The acceleration, a, in the vertical direction is just due to gravity, also
known as free fall:
ax=0
ay=−g
Velocity:
The horizontal velocity remains constant, but the vertical velocity varies
linearly, because the acceleration is constant. At any time, t, the velocity is:
ux=u⋅cosθ
uy=u⋅sinθ−g⋅t

* Maximum Height
The maximum height is reached when vy=0. Using this, we can
rearrange the velocity equation to find the time it will take for the
object to reach maximum height.
h=(u*sinθ)^2/(2*g)
* Range
The range of the motion is fixed by the condition y=0. Using this we
can rearrange the parabolic motion equation to find the range of the
motion:
R=(u)^2⋅sin2θ/g
* Parabolic Trajectory
We can use the displacement equations in the x and y direction to
obtain an equation for the parabolic form of a projectile motion:
y=(tanθ⋅x)−(g*x^2)/(2*(u^2)*(cosθ^2))

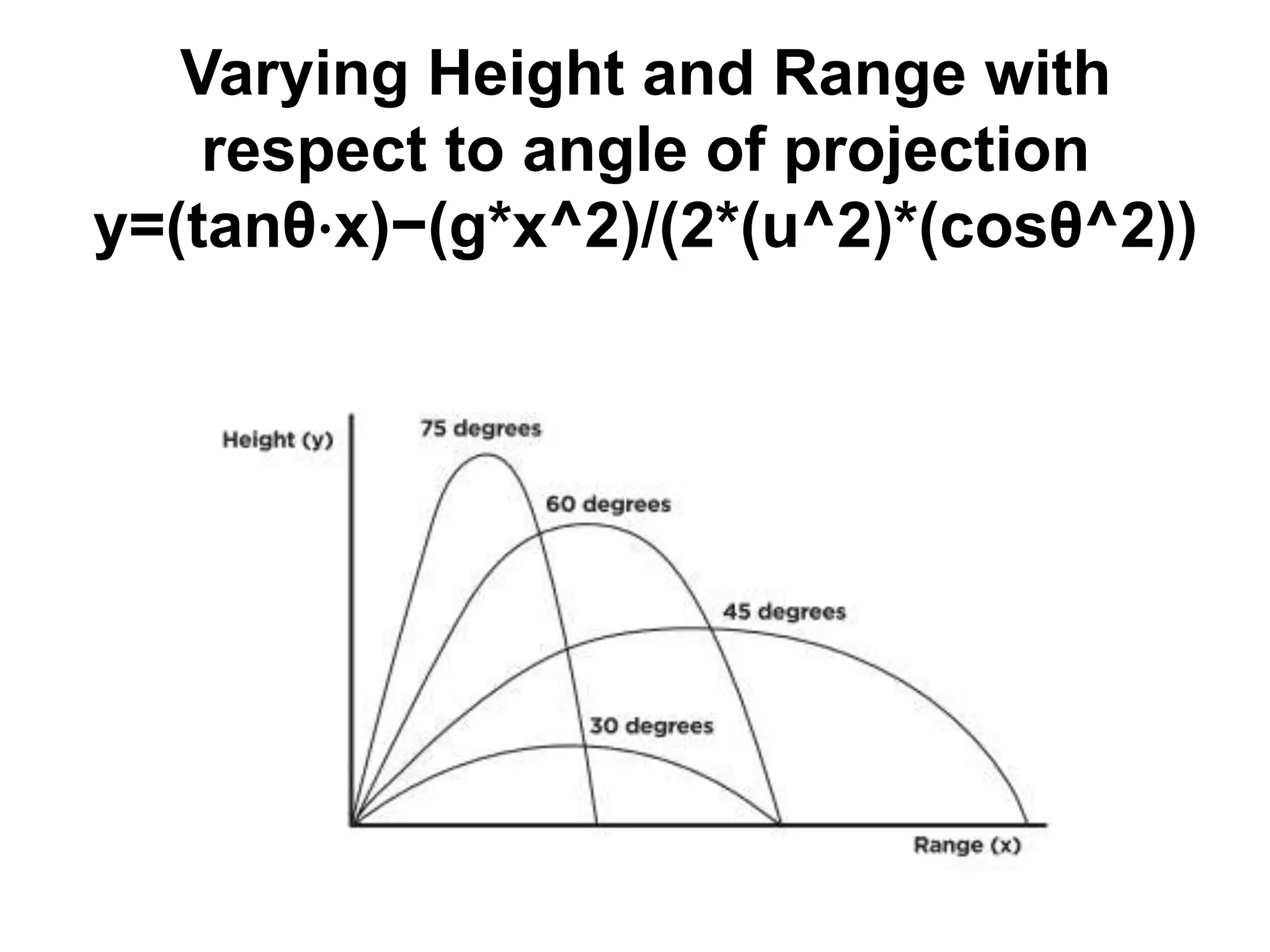
Varying Height and Range with
respect to angle of projection
y=(tanθ⋅x)−(g*x^2)/(2*(u^2)*(cosθ^2))

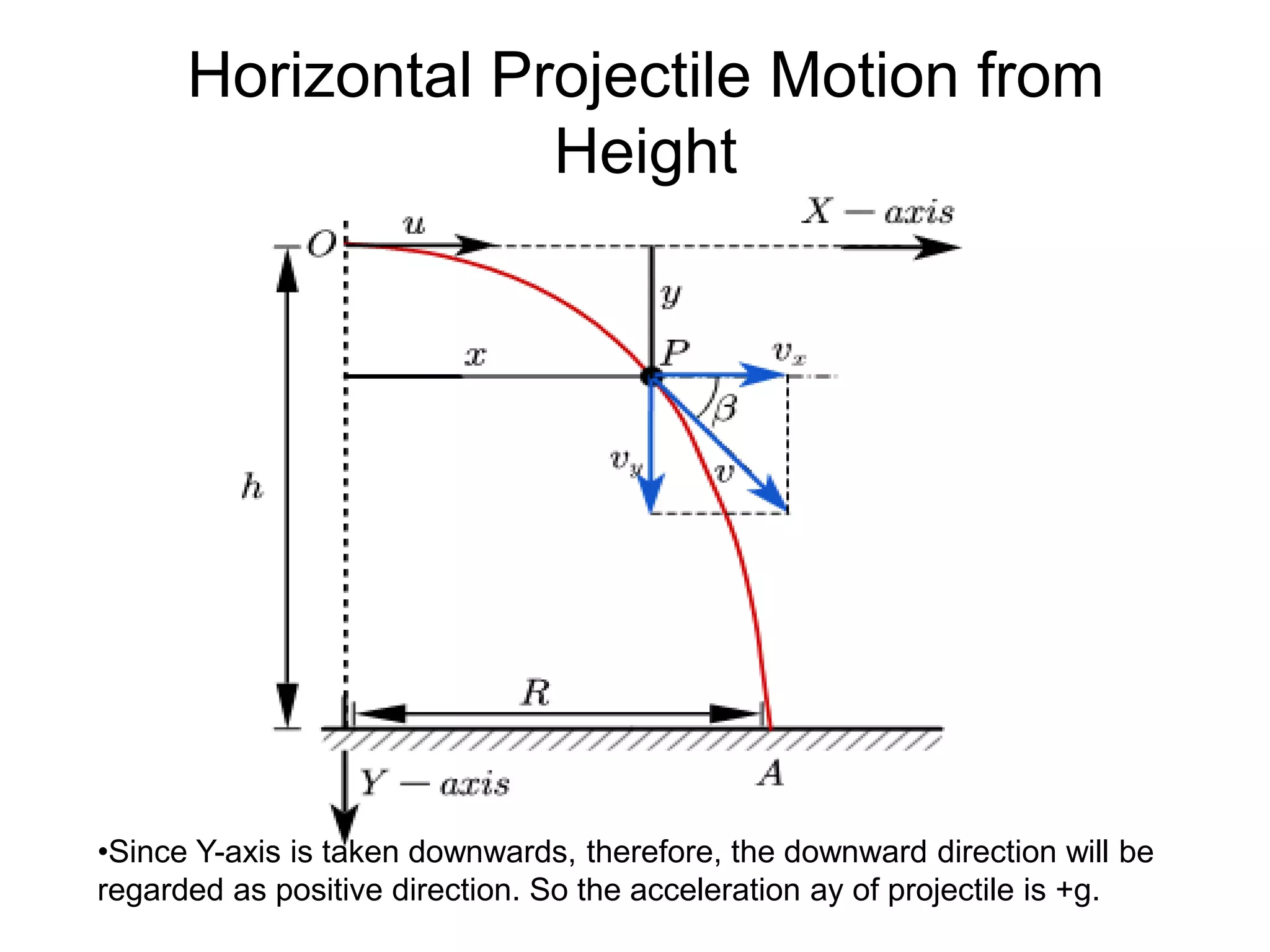
Horizontal Projectile Motion from
Height
•Since Y-axis is taken downwards, therefore, the downward direction will be
regarded as positive direction. So the acceleration ay of projectile is +g.

Horizontal Projectile Motion(Continued…)
• In this case, the projectile is launched or fired parallel to
horizontal. So, it starts with a horizontal initial velocity,
some height ‘h’ and no vertical velocity.

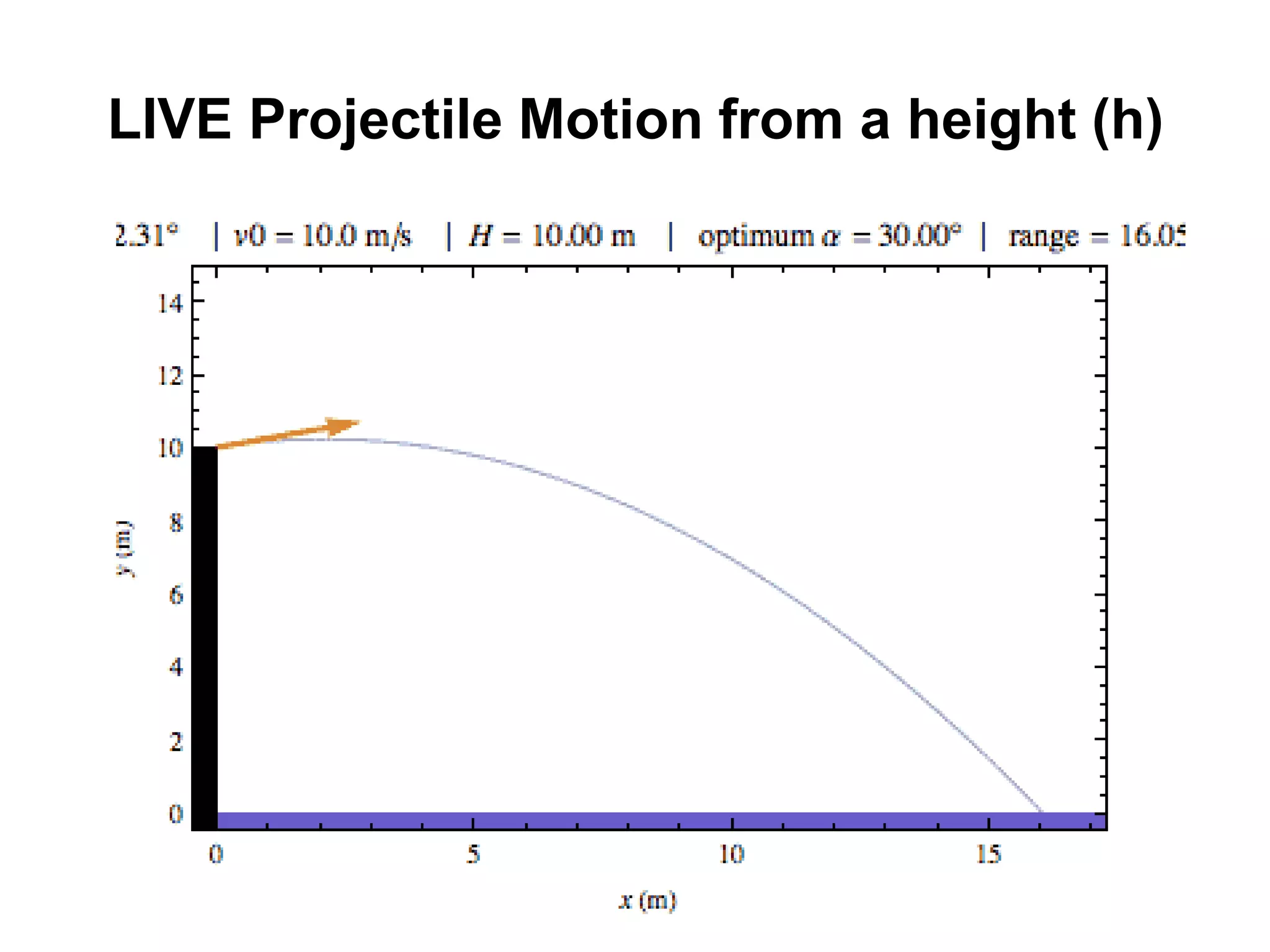
LIVE Projectile Motion from a height (h)

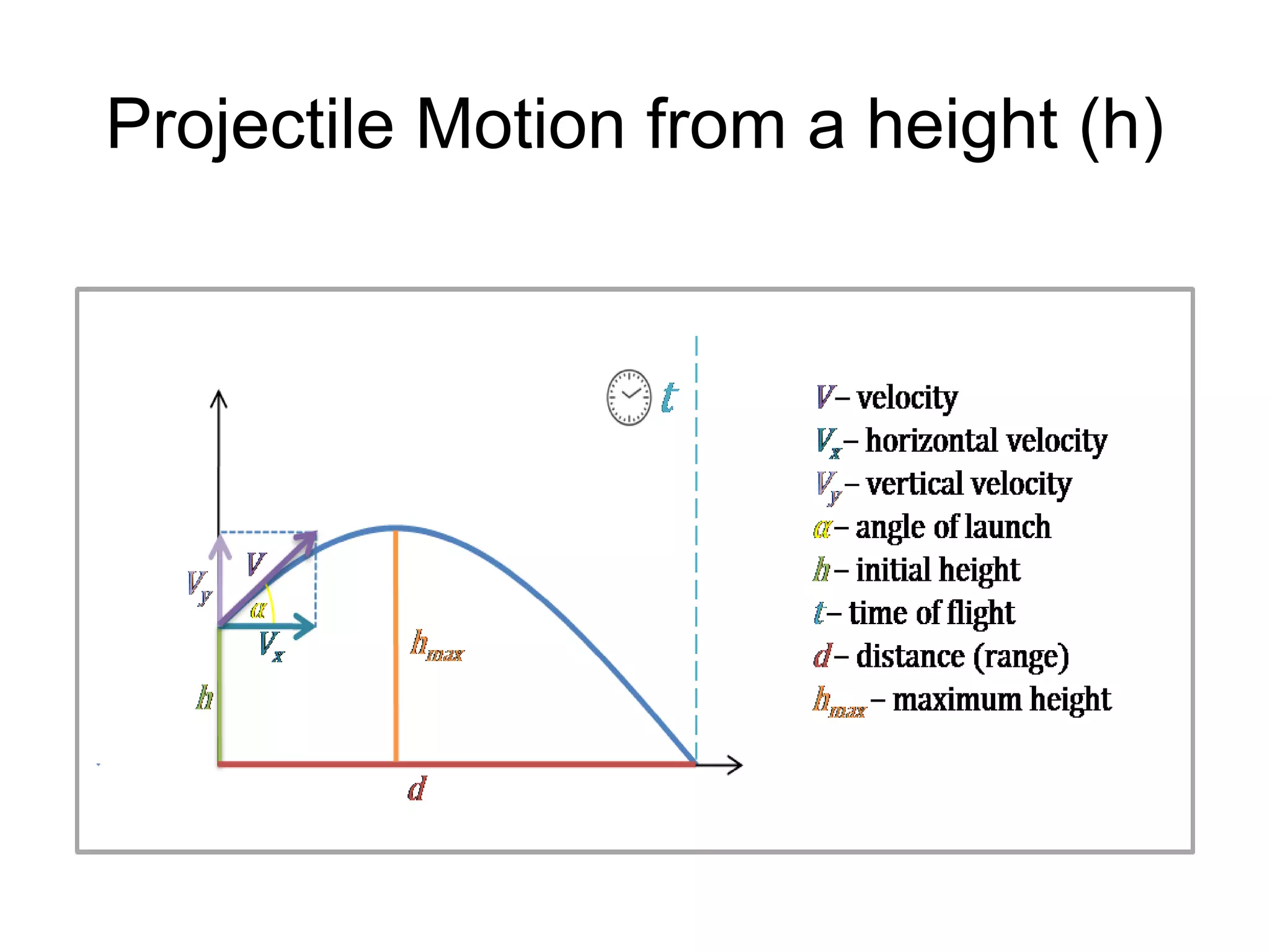
Projectile Motion from a height (h)

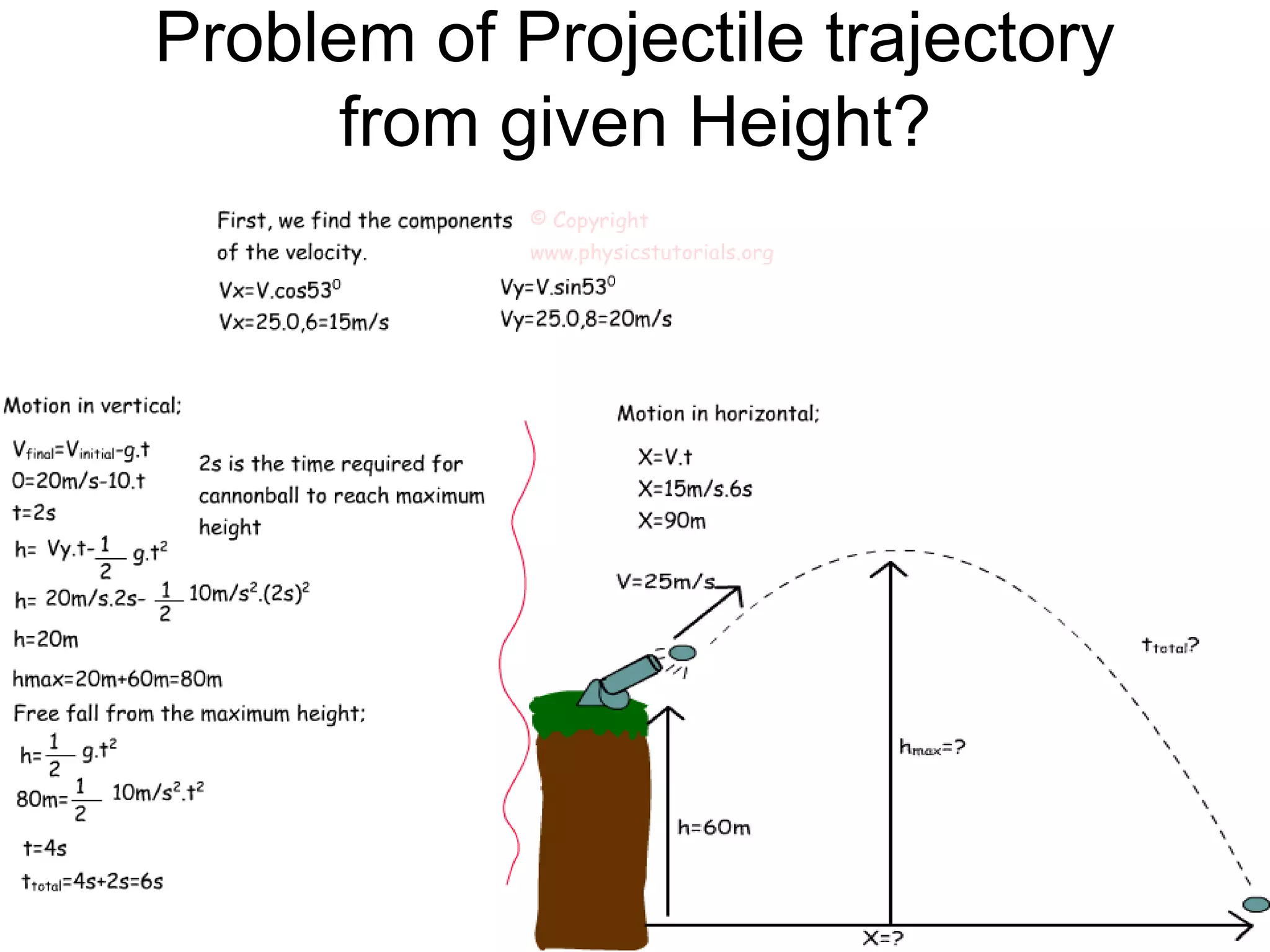
Problem of Projectile trajectory
from given Height?

Final velocity, vfinal, of projectile before
striking at ground
vyfinal^2=vy^2+2*g*h
vyfinal^2=(20m/s)^2+(2*10m/s^2*60m)
vyfinal^2=400m^2/s^2+1200m^2/s^2
vyfinal^2=1600m^2/s^2
vyfinal=40m/s
vfinal^2=vyfinal^2+vx^2
vfinal^2=(40m/s)^2+(15m/s)^2
vfinal^2=1600m^2/s^2+225m^2/s^2
vfinal=root(1825m^2/s^2)

Animated Projectile Trajectory
from given Height

What is rectilinear motion?
• Any motion in which objects or particles
take a straight path is considered
the rectilinear motion. It is also often
referred to as straight motion or rectilinear
kinematics.
• Example: Whether it is simply a girl walking straight
down a path, any vehicle or automobile driving along a
straight road, particles in the air moving in a straight,
parallel line.

Types of Rectilinear Motion
• There are three types:
• Uniform rectilinear motion: When an object travels at a constant
speed with zero acceleration it is known as uniform rectilinear
motion.
• Uniformly accelerated rectilinear motion: When an object travels
with constant acceleration it is known as uniformly accelerated
rectilinear motion.
• Rectilinear movement with non-uniform acceleration: When an
object travels at a
irregular speed and acceleration it is known
as rectilinear movement with non-uniform
acceleration.

Relative Velocity
• We encounter occasions where one or more objects move in a
frame which is non-stationary with respect to another observer.
• For example, a boat crosses a river that is flowing at some rate or
an airplane encountering wind during its motion.
• The velocity of the object A relative to the object B can be given as,
Vab=Va−Vb
• Similarly, the velocity of the object B relative to that of object a is
given by,
Vba=Vb−Va
• From the above two expressions, we can see that
Vab=−Vba
• Although the magnitude of the both the relative velocities is equal to
each other. Mathematically,
|Vab|=|Vba|

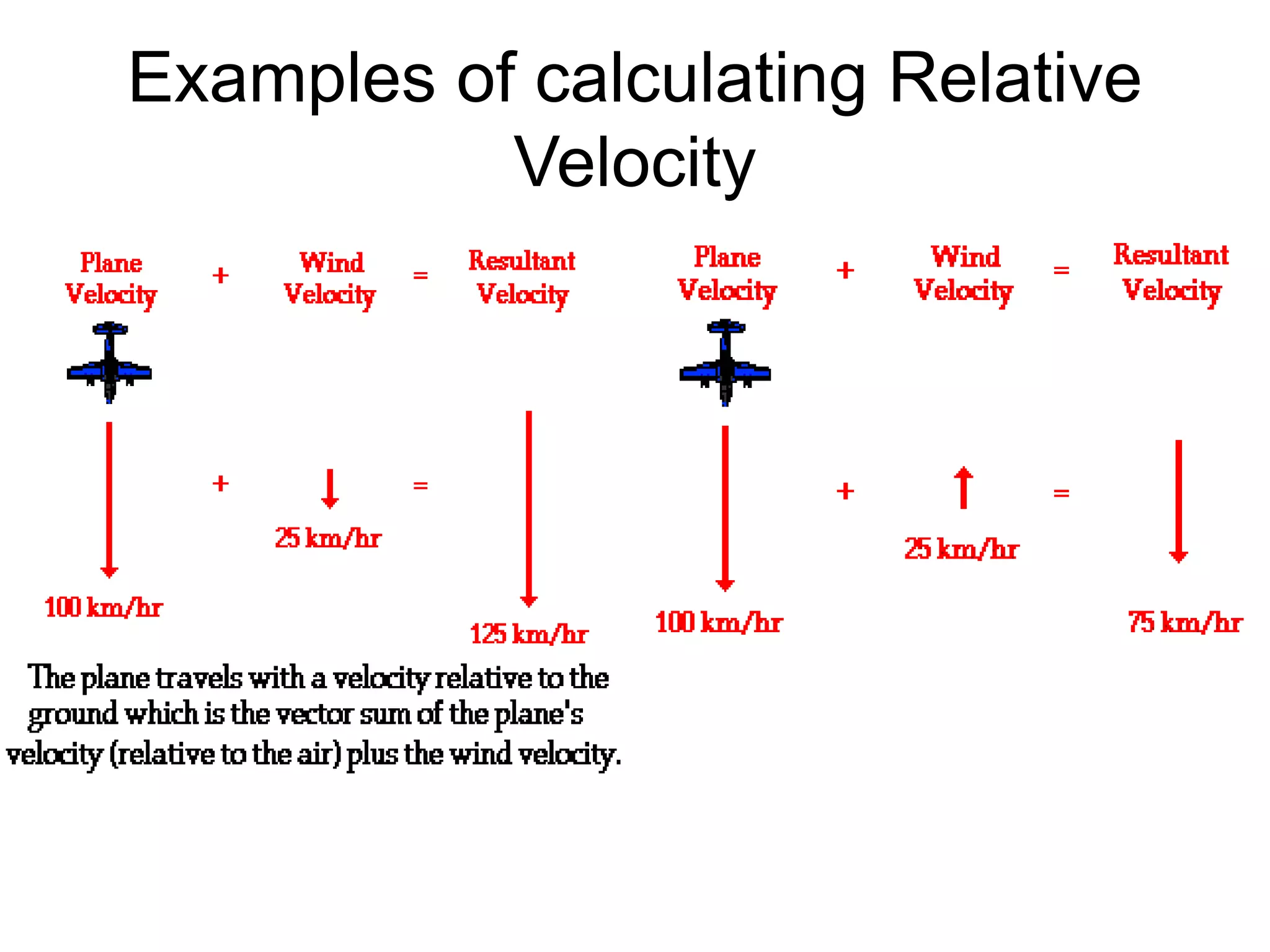
Examples of calculating Relative
Velocity

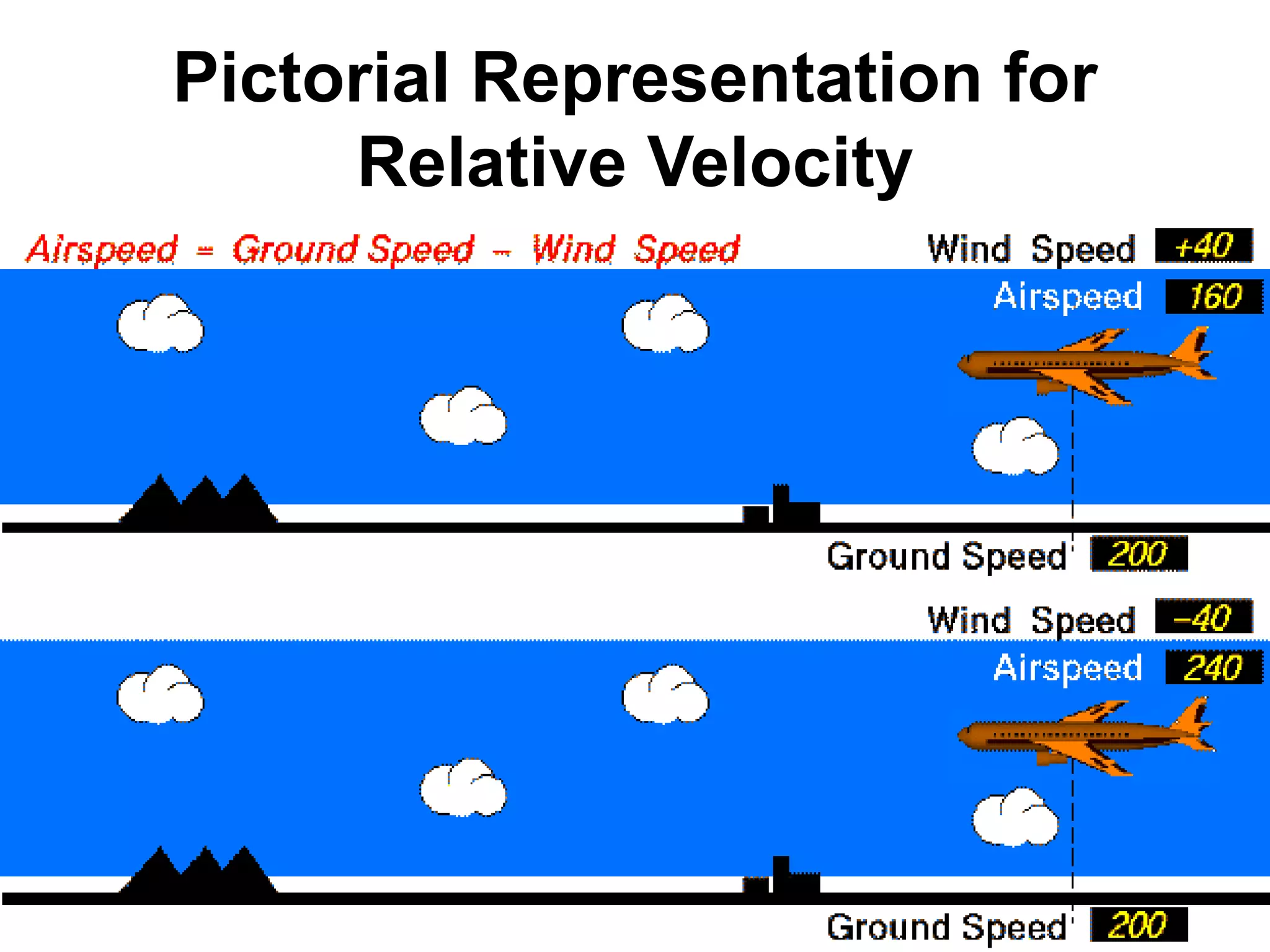
Pictorial Representation for
Relative Velocity

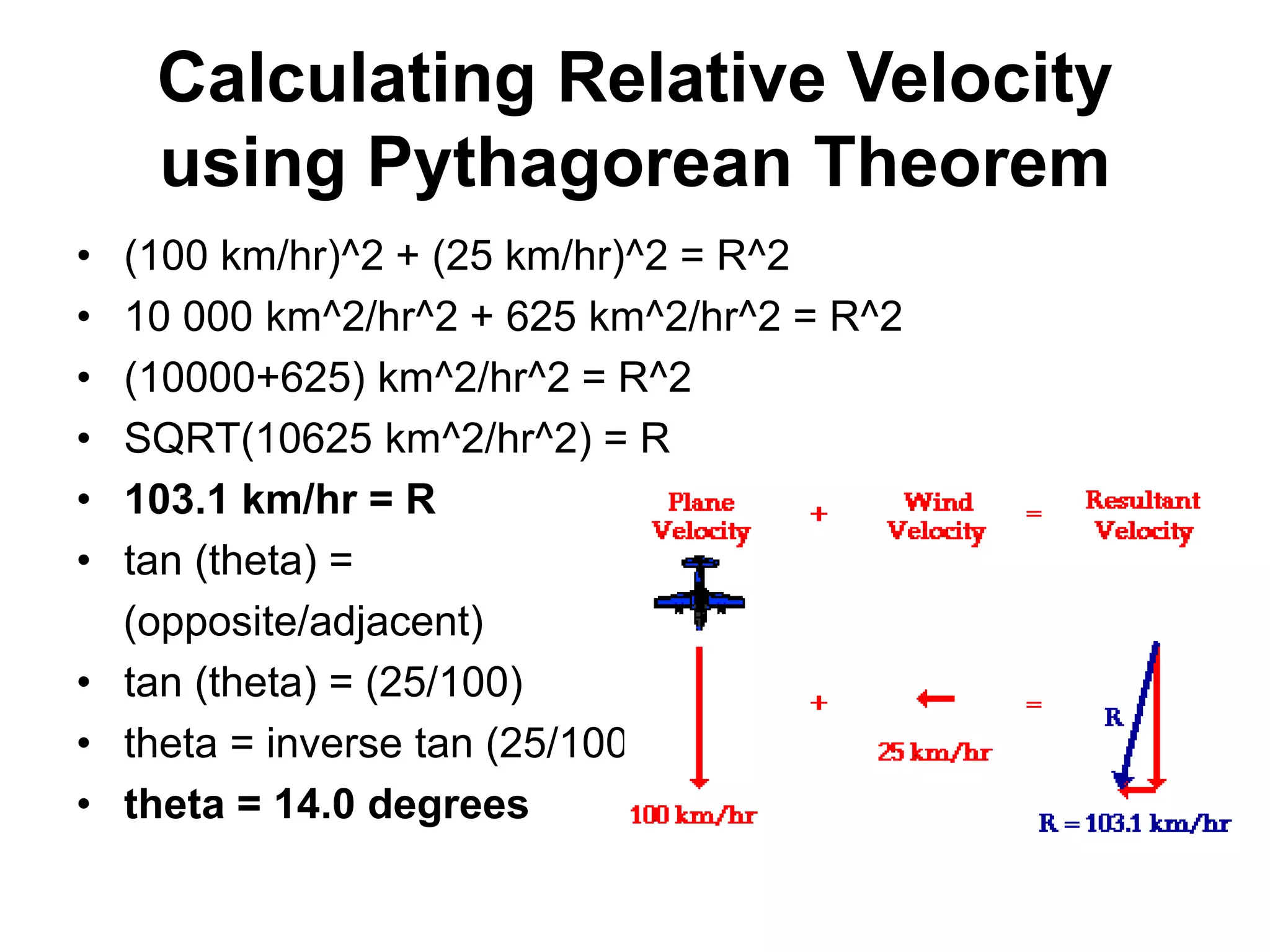
Calculating Relative Velocity
using Pythagorean Theorem
• (100 km/hr)^2 + (25 km/hr)^2 = R^2
• 10 000 km^2/hr^2 + 625 km^2/hr^2 = R^2
• (10000+625) km^2/hr^2 = R^2
• SQRT(10625 km^2/hr^2) = R
• 103.1 km/hr = R
• tan (theta) =
(opposite/adjacent)
• tan (theta) = (25/100)
• theta = inverse tan (25/100)
• theta = 14.0 degrees

Vectors and Scalars
• A vector is described by both direction and
magnitude.
• A scalar is described by only magnitude.
• Examples of scalar quantities include time,
volume, speed, mass, temperature, distance,
entropy etc.
• Example of vector quantities include
acceleration, velocity, momentum, force etc.

X and Y-Components of a Vector ‘a’

Using Scalar multiplication with
vectors
• Multiplication of a vector by a scalar changes the
magnitude of the vector, but leaves its direction
unchanged. The scalar changes the size of the vector.
Here’s how you multiply the vector
• v=<3,5>
For example, you multiply the vector
• v=<3,5>
By the scalars 2, –4, and 1/3 as follows:
• 2*v=<6,10>
• -4*v=<-12,-20>
• (1/3)*v=<1,5/3>

• Negative scalar multiplication can change
any vector’s direction .

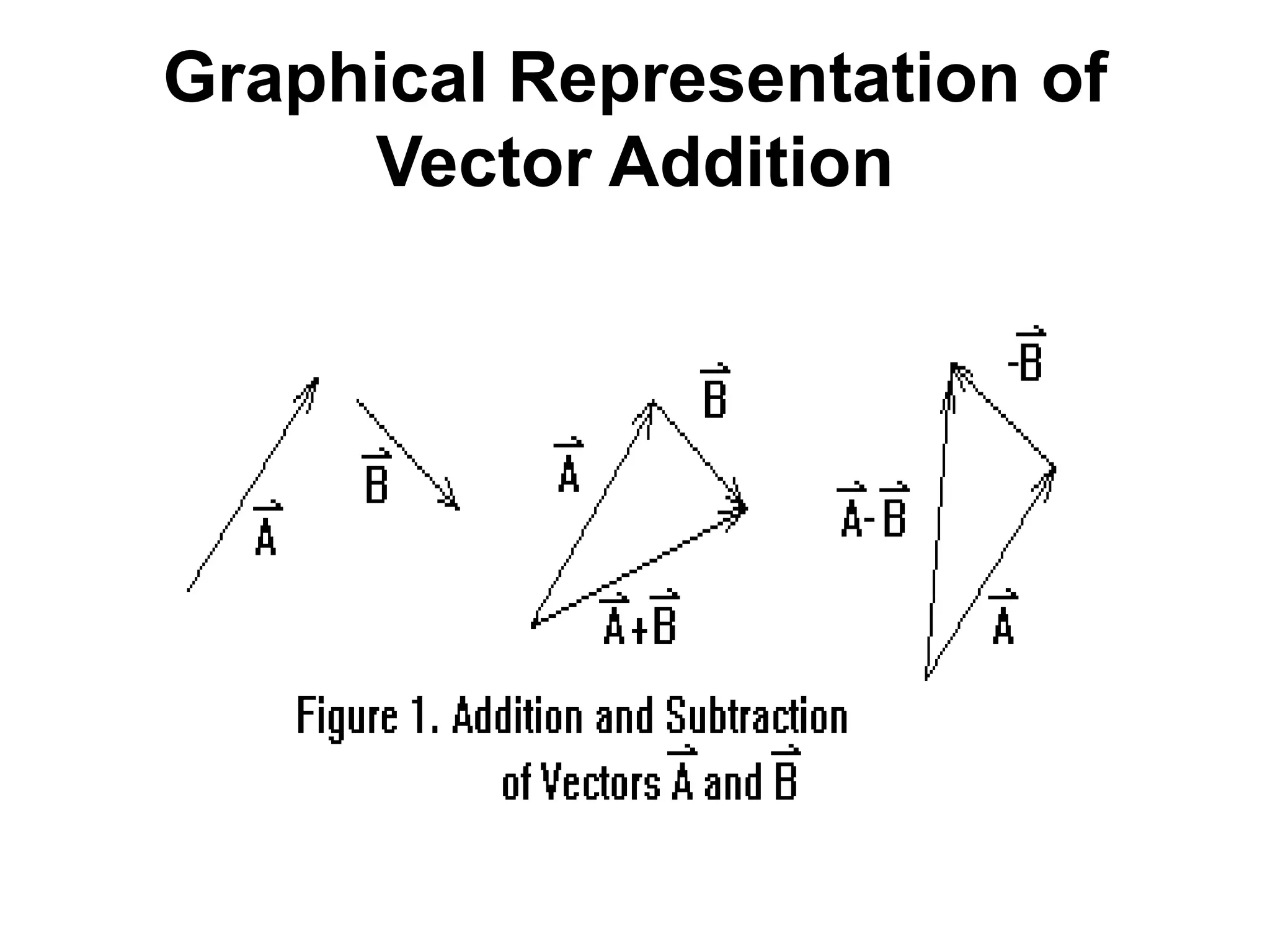
Graphical Representation of
Vector Addition

Adding 2 vectors using Triangle
Law of Vector Addition
• It is a law for the addition/subtraction of two vectors. It
can be stated as follows:
“If two vectors are represented (in magnitude and
direction) by the two sides of a triangle, taken in the
same order, then their resultant in represented (in
magnitude and direction) by the third side of the triangle
taken in same or opposite order.”
• Example1: add the vectors a = <8,13> and b = <26,7>
c = a + b
c = <8,13>+ <26,7> = <8+26,13+7> = <34,20>
• Example2: subtract k = <4,5> from v = <12,2>
a = v + −k
a = <12,2> + −<4,5> = <12,2> + <−4,−5> = <12−4,2−5> =
<8,−3>

Parallelogram Method for
addition/subtraction of two vectors
• It states that “if two vectors acting simultaneously at a
point are represented in magnitude and direction by the
two sides of a parallelogram drawn from a point, their
resultant is given in magnitude and direction by the
diagonal of the parallelogram passing through that
point.”

• (AC)^2 = (AE)2 + (EC)2
or R^2 = (P + Q cos θ)^2 +(Q sin θ)2
• or R = √(P^2+ Q^2 )+ 2PQcos θ
• And the direction of resultant from vector P will
be given by
tan(theta) = CE/AE = Qsinθ/(P+Qcosθ)
theta = tan-1 [Qsinθ/(P+Qcosθ)]

Special Cases in Parallelogram Method
(a) When θ = 0°, cos θ = 1 , sin θ = 0°
Substituting for cos θ in equation R = √(P^2+ Q^2 )+
2PQcos θ, we get,
R = √(P^2+ Q^2 )+ 2PQcos θ
= √(P+ Q)^2
or R = P+Q (maximum)
Substituting for sin θ and cos θ in equation,
Theta = tan-1 [Qsinθ/(P+Qcosθ)],
Theta = tan-1 [(Q×0)/(P+(Q×1))],
Theta = tan-1(0)
Theta = 0°

(b) When θ = 180°, cosθ = -1, sinθ = 0°
Substituting for cosθ in equation
R = √(P^2+ Q^2 )+ 2PQcos θ, we get,
R = √(P^2+ Q^2 )+ 2PQ(-1)
=√P^2+ Q^2 – 2PQ
= √(P – Q)^2 (minimum)
R = P – Q (minimum)
Substituting for sinθ and cosθ in equation,
Theta = tan-1 [(Q×0)/(P+(Q×(-1)))],
Theta = tan-1(0),
Theta = 0°

(c) When θ = 90°, cosθ = 0 ,sin θ = 1
Substituting for cosθ in equation,
R = √(P^2+ Q^2 )+ 2PQcos θ, we get,
R = √(P^2+ Q^2 )+ (2PQ×0)
R = √P^2+ Q^2
Substituting for sin θ and cos θ in equation,
Theta = tan-1 [(Q×1)/(P+(Q×(0)))],
Theta = tan-1(Q/P)

Unit Vector
• Vectors have both a magnitude (value) and a direction.
Vectors are labeled with an arrow. A unit vector is a
vector that has a magnitude of 1. They are labeled with a
“^“. Any vector can become a unit vector by dividing it by
the vector's magnitude.
Vector(v)=xi+yj+zk
Magnitude of vector,
|v|= √x^2+y^2+z^2
Unit vector(v)
=vector/magnitude of vector
=v/|v|
=v/√x^2+y^2+z^2

Example:
Given a vector, v=12i-3j-4k, find the unit vector. What is unit
vector?
Unit vector(v)=v/|v|=v/√x^2+y^2+z^2
=12i-3j-4k/√144+9+16
Unit vector(v)=12i-3j-4k/13
=(12/13)i-(3/13)j-(4/13)k
Unit vector(v)=<12/13,-3/13,-4/13>

Scaling Unit Vectors
• Scaling a geometrical vector means keeping its
orientation the same but changing its length by
a scale factor.
• For example, if vector U coordinates are (3, -7) and if
you want to scale it by two, then you multiply the
coordinates by two. Like, 3*2 and -7*2, then your new
coordinates of your vector would be, (3,-7).
Given a vector, U=<3,-7>=3i-7j, find the unit vector. and
scaling unit vector by 4?
Unit vector(U)=U/|U|=v/√x^2+y^2
=3i-7j/√9+49
Unit vector(v)=3i-7j/√58
=(3/√58)i-(7/√58)j
Scaling Unit vector(v)[=<3/√58,-7/√58 >] by 4
=<12/√58,-28/√58 >

Direction of vectors from x, nd y-
components

Plotting components of vector
‘a’=<2,1.3>=2i+1.3j on first quadrant of x,
and y-coordinate axis

Adding vectors in magnitude and
direction form
Vector v1=<23,-34>=23i-34j
Vector v2=<-19,24>=-19i+24j
Adding two vectors v1,v2,
v1+v2=<23,-34>+<-19,24>
=23i-34j-19i+24j
=4i-10j
=<4,-10>(Resultant Vector is in 4th Quardant)

Application of vectors
• Vectors can be used to represent physical quantities.
Most commonly in physics, vectors are used to
represent displacement, velocity, and acceleration, force
etc. and Vectors are a combination of magnitude and
direction, and are drawn as arrows.

What is physics

More Related Content

What's hot

Similar to What is physics

Recently uploaded

What is physics