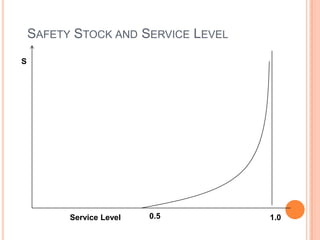
This document discusses safety stock, which is inventory kept on hand to reduce the risk of temporary shortages due to variations in demand or delays in supply. It provides three key points: 1) Safety stock helps absorb variability in customer demand forecasts and lead times to improve customer service levels and prevent stockouts. 2) The right level of safety stock is important - too much wastes money in holding costs but too little can lead to lost sales from stockouts. 3) Safety stock is calculated based on the expected demand during the lead time and the variability or uncertainty in demand and lead times, using methods like percentage of lead time demand or number of days supply.

1. SAFETY STOCKS
By:SHASHANK SHEKHER SINGH- 83
VIKAS SINGH-104
KUMAR RAVI-111
ANKIT SEMWAL -125
WAZIBUR REHMAN-106
NIKUNJ SHARMA-143

2. SAFETY STOCKS DEFINED
Safety stock is a term that is used to describe the
amount of inventory or stock that is kept on hand in
order to reduce the chance of a temporary shortfall
of materials from taking place.
 Also known as buffer stock.
 This type of inventory is helpful in dealing with
sudden upswings in demand or just for making sure
there are enough raw materials and supplies on
hand to keep production going while waiting for the
next scheduled delivery of materials from a
supplier.


3. CONTINUED..
The amount of safety stock an organization
chooses to keep on hand can dramatically affect
their business.
 Too much safety stock can result in high holding
costs of inventory. In addition, products which are
stored for too long a time can spoil, expire, or break
during the warehousing process.
 Too little safety stock can result in lost sales
and, thus, a higher rate of customer turnover. As a
result, finding the right balance between too much
and too little safety stock is essential.


4. WHY SAFETY STOCKS ARE NEEDED?
The main goal of safety stocks is to absorb the
variability of the customer demand.
 Indeed, the Production Planning is based on a
forecast, which is (by definition) different from the
real demand.
 By
absorbing these variations, safety stock
improves the customer service level.
 By creating a safety stock, you will also prevent
stock-outs from other variations :

an upward trend in the demand
 a problem in the incoming product flow (machinery
breakdown, supplies delayed, strike, ...)


5. UNCERTAINTIES IN INVENTORY MANAGEMENT

In actual case of inventory model, there are always
uncertainties stemming from two basic reasons:
 Variability in sales, hence variability in the demand for the
materials or the consumption of the material.
 Delay in supply of raw material.

Demand is a prediction based on past history, trend
factor(s), and/or known future usage of a product. The item’s
actual usage will probably be more or less than this quantity.
Safety stock is needed for those occasions when actual usage
exceeds forecasted demand. It is “insurance” to help ensure
that you can fulfill customer requests for a product during the
time necessary to replenish inventory.

6. 
The anticipated lead time is also a prediction, usually
based on the lead times from the last several stock
receipts. Sometimes the actual lead time will be greater
than what was projected. Safety stock provides
protection from stock outs when the time it takes to
receive a replenishment shipment exceeds the projected
lead time.

7. SERVICE LEVEL

Service level (denoted as Fx) is typically measured
as Fx = (demand filled) over (total demand).

Service level may also be defines as demand
fulfilled over a particular period of time.

Service Level may also be defined as the Ratio of
„No of units supplied without delay‟ and „No of units
demanded‟

8. SAFETY STOCK AND SERVICE LEVEL
 Safety
stock determines the chance of a stockout
during lead time
 The complement of this chance is called the service
level
 Service level is defined as the probability of not
incurring a stockout during any one lead time
 The higher the probability inventory will be on
hand, the more likely customer demand will be met.
 Service level of 90% means there is a .90
probability that demand will be met during lead time
and .10 probability of a stockout.

9. SAFETY STOCK AND SERVICE LEVEL
S
Service Level
0.5
1.0

10. RISK LEVEL

Defined as the percentage of demand that will not
be fulfilled during a particular period of time

Service level= 1- Risk level

11. SAFETY STOCK AND REORDER POINT

Without safety stock:
R nL
where R

With safety stock:
reorder point in units
n
daily demand in units
L
lead time in days
R nL SS
where SS
safety stock in units

12. SAFETY STOCK EXAMPLE
Daily demand = 20 units

Lead time = 10 days

S.D. of lead time demand = 50 units

Service level = 90%
Determine:

1.
2.
Safety stock
Reorder point

13. SAFETY STOCK SOLUTION
Step 1 – determine z
From Appendix B :
z 1.28
Step 2 – determine safety stock
SS 1.28 50 64 units
Step 3 – determine reorder point
R
nL SS
20 10 64 264 units

15. CALCULATION OF SERVICE LEVEL
can also be calculated by equating Carrying cost
per unit per annum with shortage cost per unit per
annum.

i.e. Cc = Cs
= Csus * Prob. Of shortage * Number of
times shortage situations can occur
in a year
= Csus * (1 – Fx) * R/Q
 (1 – Fx) = Cc * (Q R) * 1 / Csus
Fx = 1 - Cc * (Q R) * 1 / Csus


16. CONTD.

Another formula for service level is
Fx=Ku/(Ku+Ko)
being
Ku= Under stocking cost
Ko=Overstocking cost

17. NUMERICAL
Ajay bakery makes ginger bread; one of its fastest
selling products. From past history Ajay estimates the
demand pattern to be:
Demand(no. of buns)
Probability of Demand
400
0.05
500
0.10
600
0.20
700
0.30
800
0.20
900
0.10
1000
0.05
The selling price of each bread is 80 paise. The buns
that are not sold on the day they are made, are sold the
next day at the reduced price of 40 paise each. If the
cost of each bun is 55 paise, what is optimum number
of buns Ajay should make?

18. Here Ku the understocking cost, is the profit
forgone, which is the difference between sales price
per unit and unit cost: (80p – 55p)= 25p
Ko, the overstocking cost, is the loss in the sale on
the next day; which is the difference between the
cost per unit and the salvage value per unit:
55p – 40p= 15p
Fx=Ku/(Ku+Ko)= 0.25/0.25+0.15=0.625

19. Cumm.
frequency
Demand(no. of buns)
Probability of Demand
400
0.05
0.05
500
0.10
0.15
600
0.20
0.35
700
0.30
0.65
800
0.20
0.85
900
0.10
0.95
1000
0.05
1.00
This is met at x=700, where the cumulative
probability is 0.650 slightly exceeding the value
0.625

20. THE CONVENTIONAL WAYS OF CALCULATING
SAFETY STOCK
There are two common conventional methods for
calculating the safety stock quantity for a product:
 Percentage of Lead Time Demand
 Days Supply
 It refer to two variables, “forecast demand” and
“usage.” Forecast demand is a prediction of how
much of a product will be sold or otherwise used in
a particular month, and usage is the quantity that
was actually sold or used.


21. Percentage of Lead Time Demand
Inventory consultant Gordon Graham long advocated
that, for most items, 50% of lead time demand provides
an adequate safety stock quantity. Let’s look at an
example:
Demand/Day = (390/30) = 13 pieces
Projected Lead Time = 8 days
Demand During the Lead Time = (8 x 13) = 104
pieces
Safety Stock = (104 x 50%) = 52 pieces

22. This method is easy to understand but it tends to maintain
too much or too little safety stock for many items. For
example:
 Products with long but very reliable lead times and with
fairly consistent demand. If we use this method for an
imported product with a 12-week lead time, we’ll keep six
weeks stock in reserve as safety stock. If we usually receive
the shipment on time and demand doesn’t vary substantially
from month to month, we’ll have too much safety stock – in
other words, too much money tied up in non-productive
inventory.


23. 
Products with very short lead times and significant variations in
demand from month to month. If a product had a one-week lead
time, this method will keep a three or day supply of the item in
reserve as safety stock. If usage tends to vary significantly from
month to month, there probably won’t be enough safety stock
available to consistently fill customer demand and the company will
experience stock outs.
DAYS SUPPLY

The days supply method allows a buyer to manually specify a
number of days supply of a product to hold in reserve as
safety stock. Because a buyer usually does not have the time
to review the safety stock parameters for every item each
month, he or she will probably set the days supply to provide
more than enough safety stock. After all, in the eyes of most
buyers, excess inventory is usually preferable to stock outs.
As a result, the days supply method often results in the
accumulation of non-producing inventory.

24. SAFETY STOCK CALCULATION FOR CONSTANT
LEAD TIME AND NORMALLY DISTRIBUTED DDLT
The projected level of demand for a product from
consumers during its lead time from the supplier to
the retailer
 For the desired service level, find the value of “Z”
from the table “Area under Normal Curve”
 Other notations are


µL be Mean demand during lead time (DDLT)
 σL be standard deviation of demand during lead time

let x be stock at which order is placed

25. CONTD.

((X - µL)/σL = Z

Safety stock is = Z x σL

26. Continuous System: Deterministic Model

27. Reorder Point
• The reorder point is the inventory level at which a new
order is placed.
• Order must be made while there is enough stock in place to
cover demand during lead time.
• Formulation:
•R = dL
•where d = demand rate per time period
•
L = lead time

28. Reorder Point and Safety Stock

29. NUMERICAL 1

ABC Ltd. is engaged in production of tires. It
purchases rims from DEL Ltd. an external supplier.
DEL Ltd. takes 10 days in manufacturing and
delivering an order. ABC's requires 10,000 units of
rims. Its ordering cost is $1,000 per order and its
carrying costs are $3 per unit per year. The
maximum usage per day could be 50 per day.
Calculate safety stock.

30. SOLN.
Maximum daily usage is 50 units and average daily
usage is 27.4 (10,000 annual demand ÷ 365 days).
 Safety Stock = (50-27.4) × 10 = 226 units.
 Reorder Level = Safety Stock + Average Daily
Usage × Lead Time
 Reorder Level = 226 units + 27.4 units × 10 = 500
units.


31. NUMERICAL 2

Costas Hamburger Shop uses 20 gallons of cola
per day. The lead time is normally distributed with a
mean of 5 days and a standard deviation of 2 days.
Determine the level of safety stock and optimal
reorder point. Assume a service level of 99%.

32. SOLN.
ROP = Expected demand during lead time + safety
stock
d = 20 gallons per day.
LT= 5 days.
σLT = 2 days.
For a service level of 99%, z = 2.33.
Safety stock = 2.33 (20)(2) = 93.2 gallons.
ROP = 20(5) + 93.2 = 193.2 gallons


33. NUM. 3

Presume that Litely carries a modern white kitchen
ceiling lamp that is quite popular. The anticipated
demand during lead-time can be approximated by a
normal curve having a mean of 180 units and a
standard deviation of 40 units. What safety stock
should Litely carry to achieve a 95% service level?

34. To find the safety stock for a 95% service level it is necessary to calculate the 95th percentile on
the normal curve. Using the standard Normal table from the text, we find the Z value for 0.95 is
1.65 standard units. The safety stock is then given by:
(165* 40) 180 66 180 246 Ceiling Lamps
.

35. A TV dealer finds the cost of holding a TV in stock for a
week as Rs 30 and cost of unit shortage as Rs 70. For a
particular model of TV, the weekly sales distribution is given in
the table below. How many units should the dealer order per
week?
Sales 0
1
2
3
4
5
6
Prob. 0.05 0.10 0.20 0.25 0.20 0.15 0.05

36. SAFETY STOCK – EXAMPLE 3 (SOLUTION)
Weekly Cc = Rs. 30 , Cs = Rs. 70
Ordering Strategy / Week
D
Pr
0
0.05
1
0.10
2
0.20
3
0.25
4
0.20
5
0.15
6
0.05

37. Weekly Cc = Rs. 30 , Cs = Rs. 70
SAFETY STOCK – EXAMPLE 3 (SOLUTION)
Ordering Strategy / Week
D
Pr
0
0.05
1
0.10
2
0.20
3
0.25
4
0.20
5
0.15
6
0.05
0
1
2
3
4
5
6

38. Weekly Cc = Rs. 30 , Cs = Rs. 70
SAFETY STOCK – EXAMPLE 3 CONTD.
Ordering Strategy / Week
D
Pr
0
0.05 0
1
0.10 70
2
0.20 140
3
0.25 210
4
0.20 280
5
0.15 350
6
0.05 420
Expect
ed cost
0
1
2
3
4
5
6

39. SAFETY STOCK – EXAMPLE 3 CONTD.
Ordering Strategy / Week
D
Pr
0
1
2
3
4
0.05 0
30
60
90
120 150 180
1
0.10 70
0
30
60
90
120 150
2
0.20 140 70
0
30
60
90
120
3
0.25 210 140 70
0
30
60
90
4
0.20 280 210 140 70
0
30
60
5
0.15 350 280 210 140 70
0
30
6
0.05 420 350 280 210 140 70
Expect
ed cost
0
5
6
0

40. SAFETY STOCK – EXAMPLE 3 CONTD.
Ordering Strategy / Week
D
Pr
0
1
2
3
4
0.05 0
30
60
90
120 150 180
1
0.10 70
0
30
60
90
120 150
2
0.20 140 70
0
30
60
90
120
3
0.25 210 140 70
0
30
60
90
4
0.20 280 210 140 70
0
30
60
5
0.15 350 280 210 140 70
0
30
6
0.05 420 350 280 210 140 70
Expect
ed cost
0
97
5
6
0

41. SAFETY STOCK – EXAMPLE 3 CONTD.
Ordering Strategy / Week
D
Pr
0
1
2
3
0
0.05
0
30
60
90
120 150 180
1
0.10
70
0
30
60
90
120 150
2
0.20 140
70
0
30
60
90
120
3
0.25 210 140
70
0
30
60
90
4
0.20 280 210 140
70
0
30
60
5
0.15 350 280 210 140
70
0
30
6
0.05 420 350 280 210 140
70
0
62
87
Expect
ed cost
217 152
97
62
4
52
5
6

42. SAFETY STOCK – EXAMPLE 3 CONTD.
Ordering Strategy / Week
D
Pr
0
1
2
3
0
0.05
0
30
60
90
120 150 180
1
0.10
70
0
30
60
90
120 150
2
0.20 140
70
0
30
60
90
120
3
0.25 210 140
70
0
30
60
90
4
0.20 280 210 140
70
0
30
60
5
0.15 350 280 210 140
70
0
30
6
0.05 420 350 280 210 140
70
0
62
87
Expect
ed cost
217 152
97
62
4
52
5
6

43. EXAMPLE 4
Sai electrical buy electrical switches for the
assembly of variety of electrical products. Sai
observes that the usage pattern of these boughtout switches follow normal distribution with a mean
of 1000 switches per week and a standard
deviation of 200. the buying process takes one
week. The inventory holding cost is Rs.5/- per unit
and the cost of ordering is Rs. 200/- per order. Sai
allows for only 2 stock out situation in a year.
Compute the safety stock required.

44. Thank you