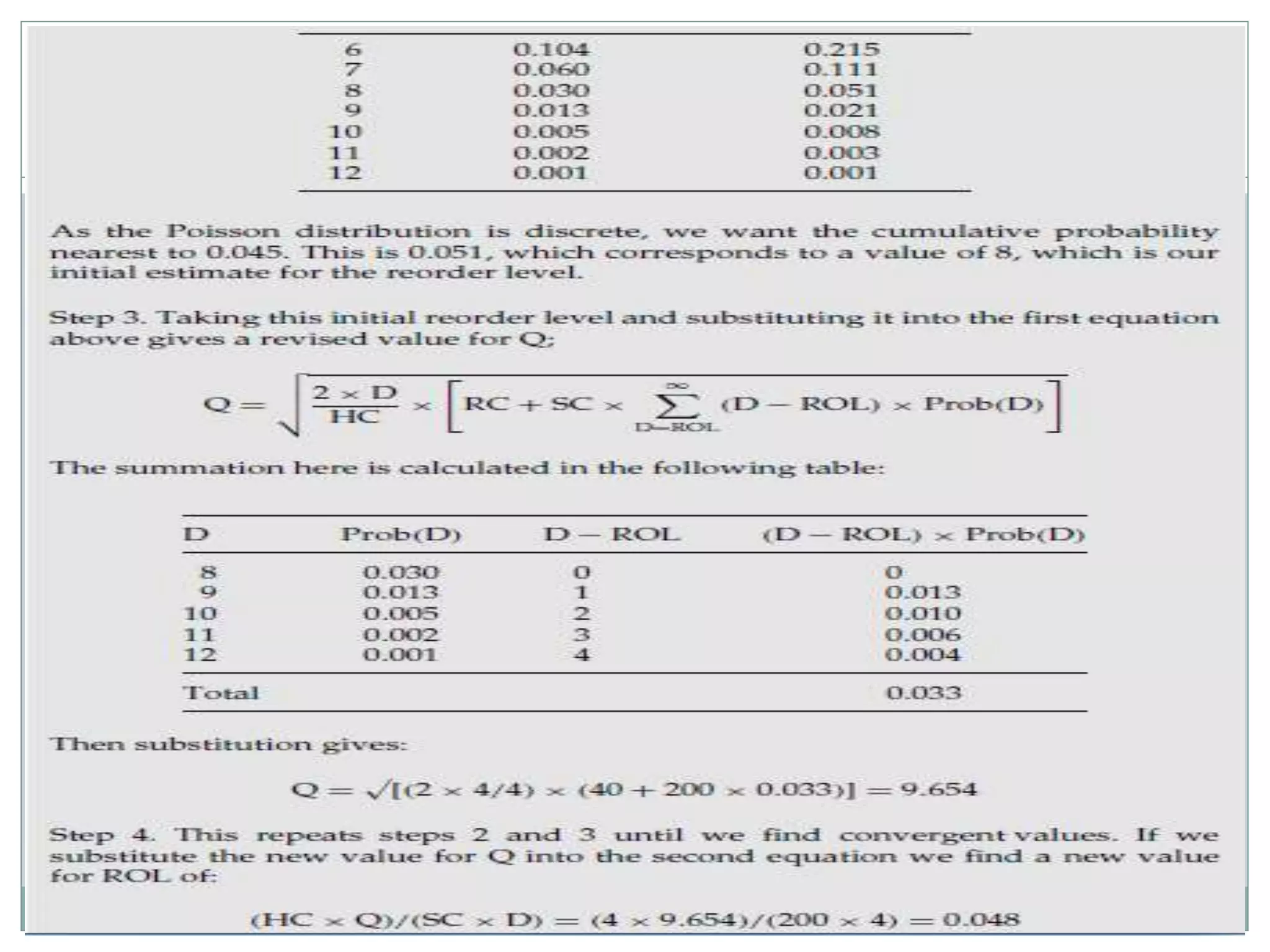
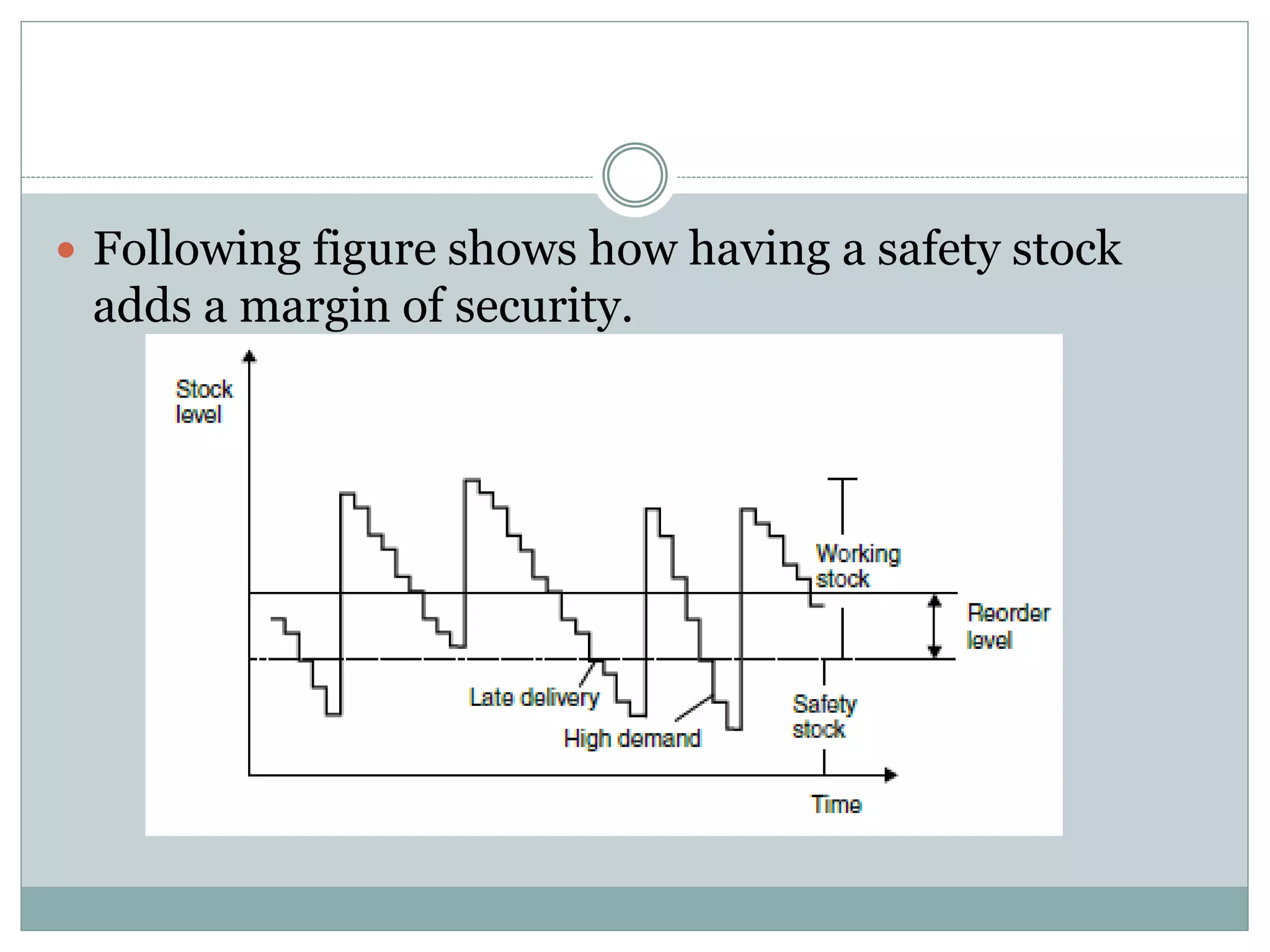
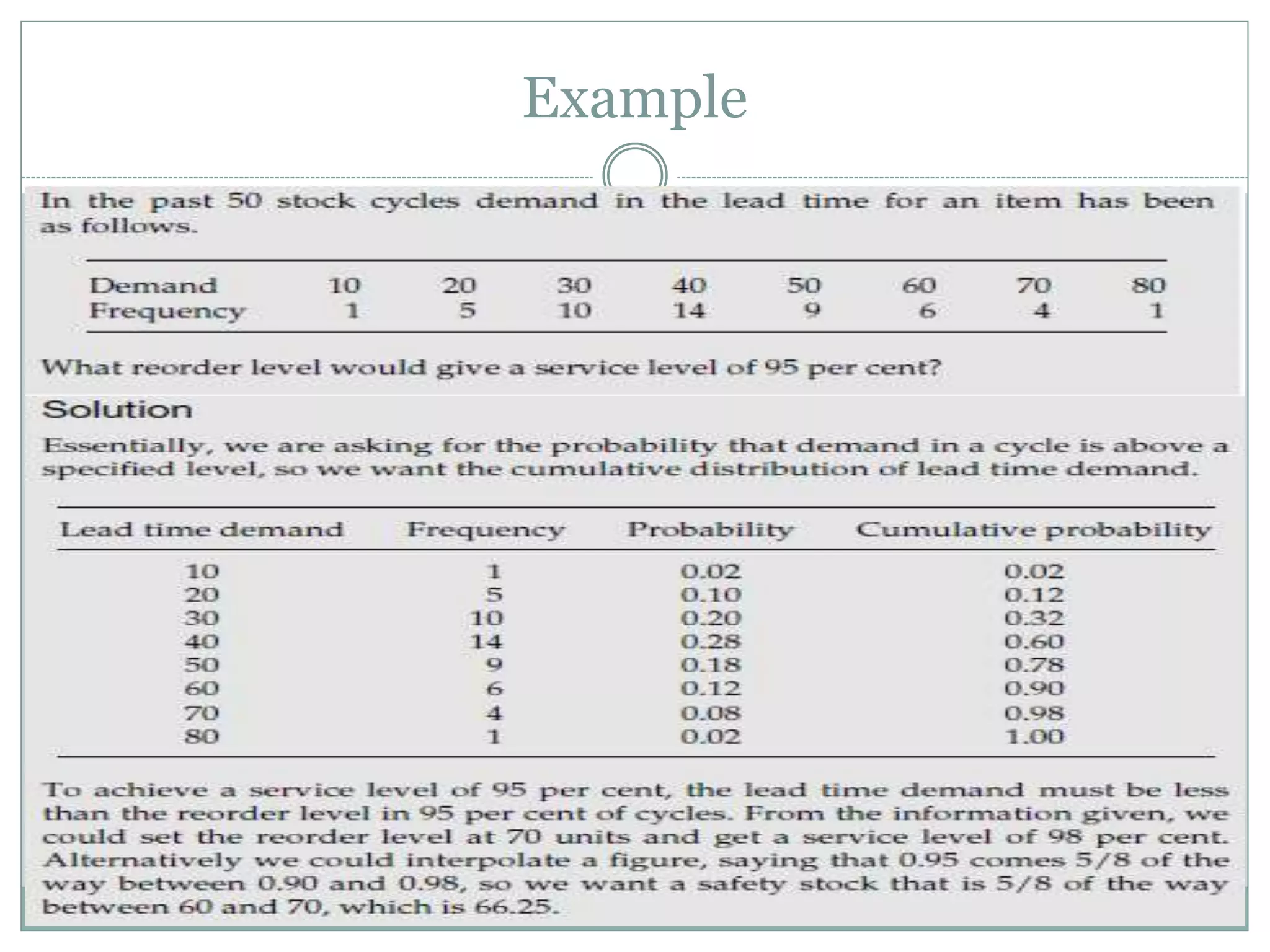
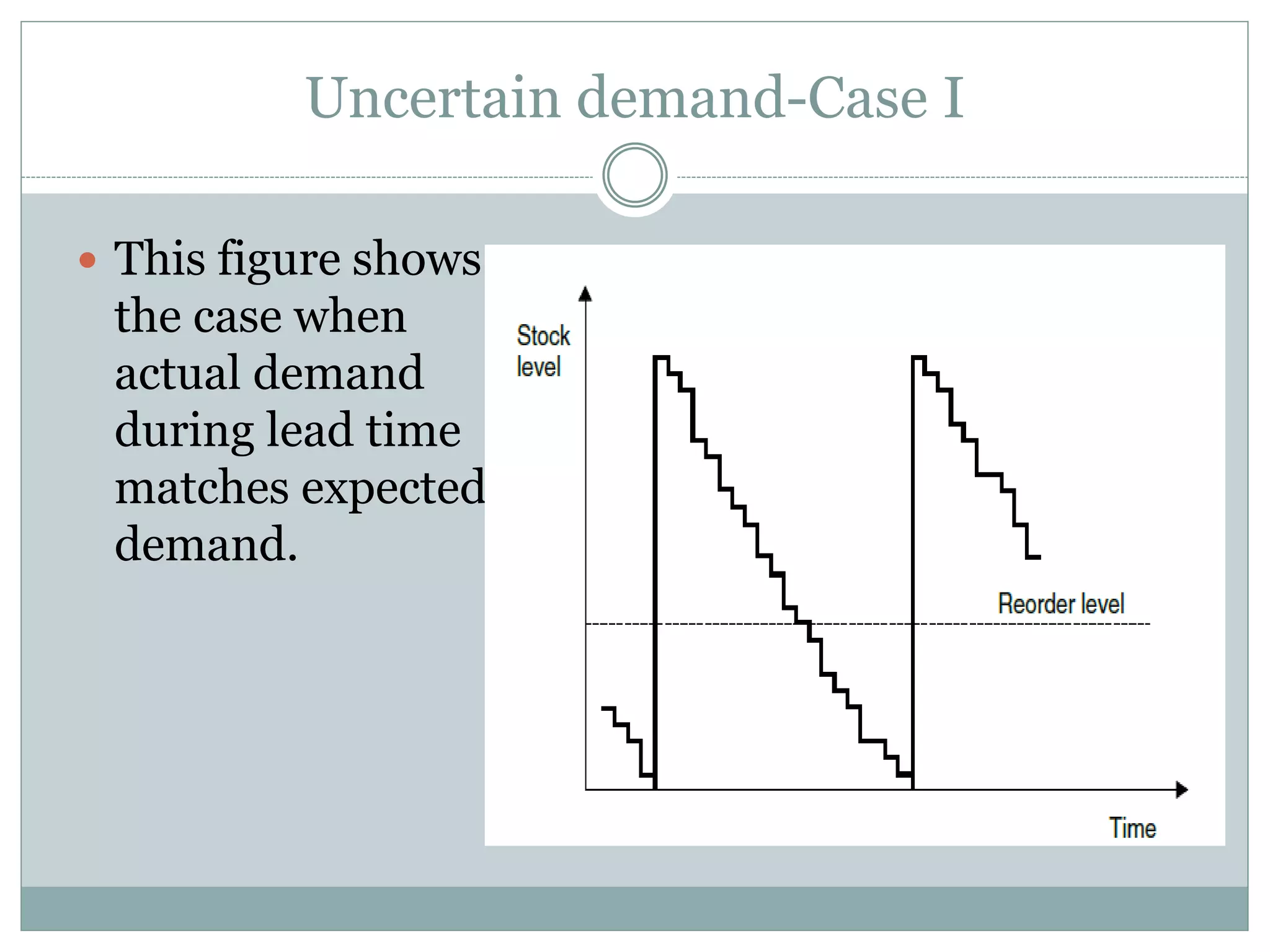
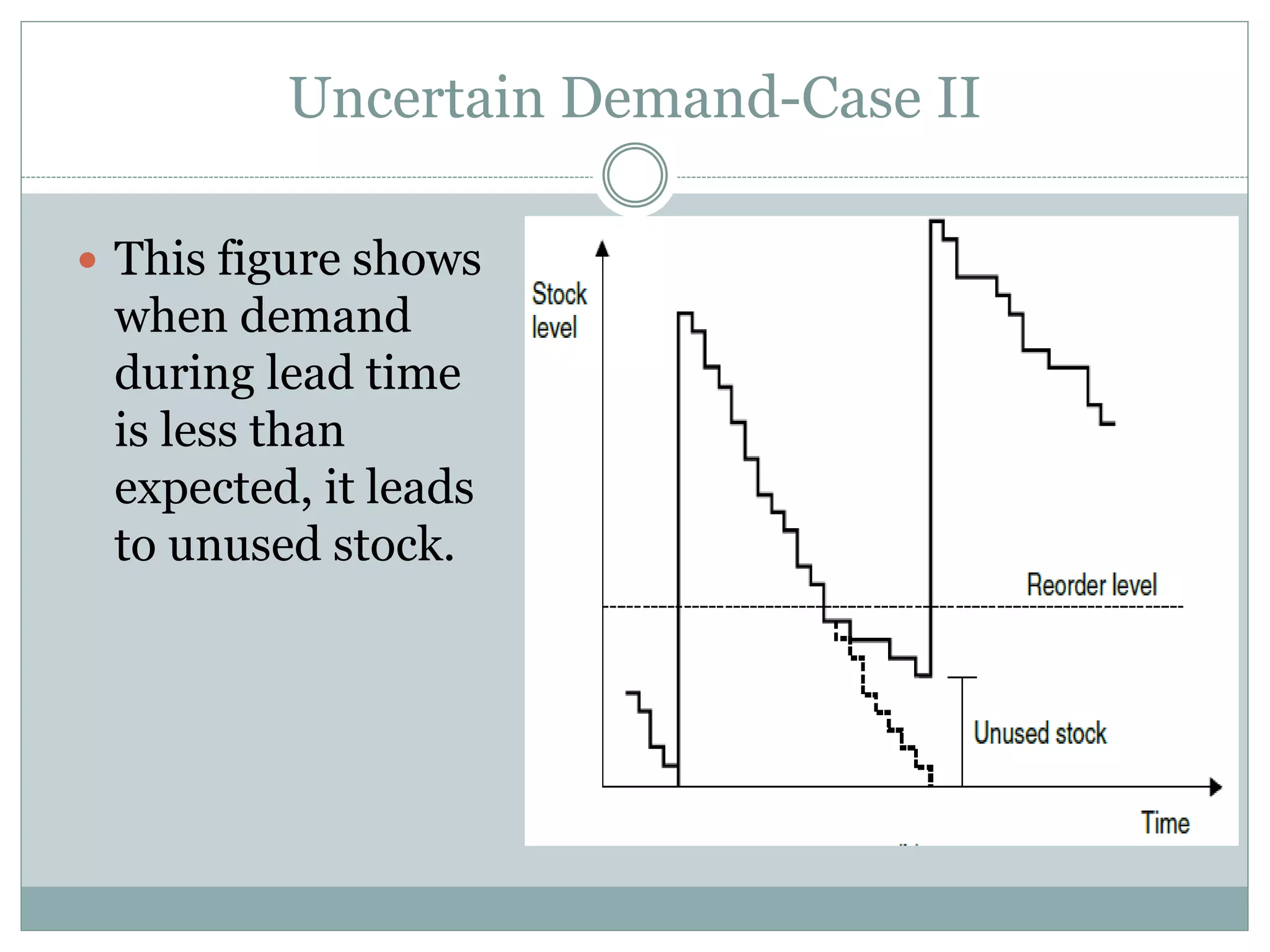
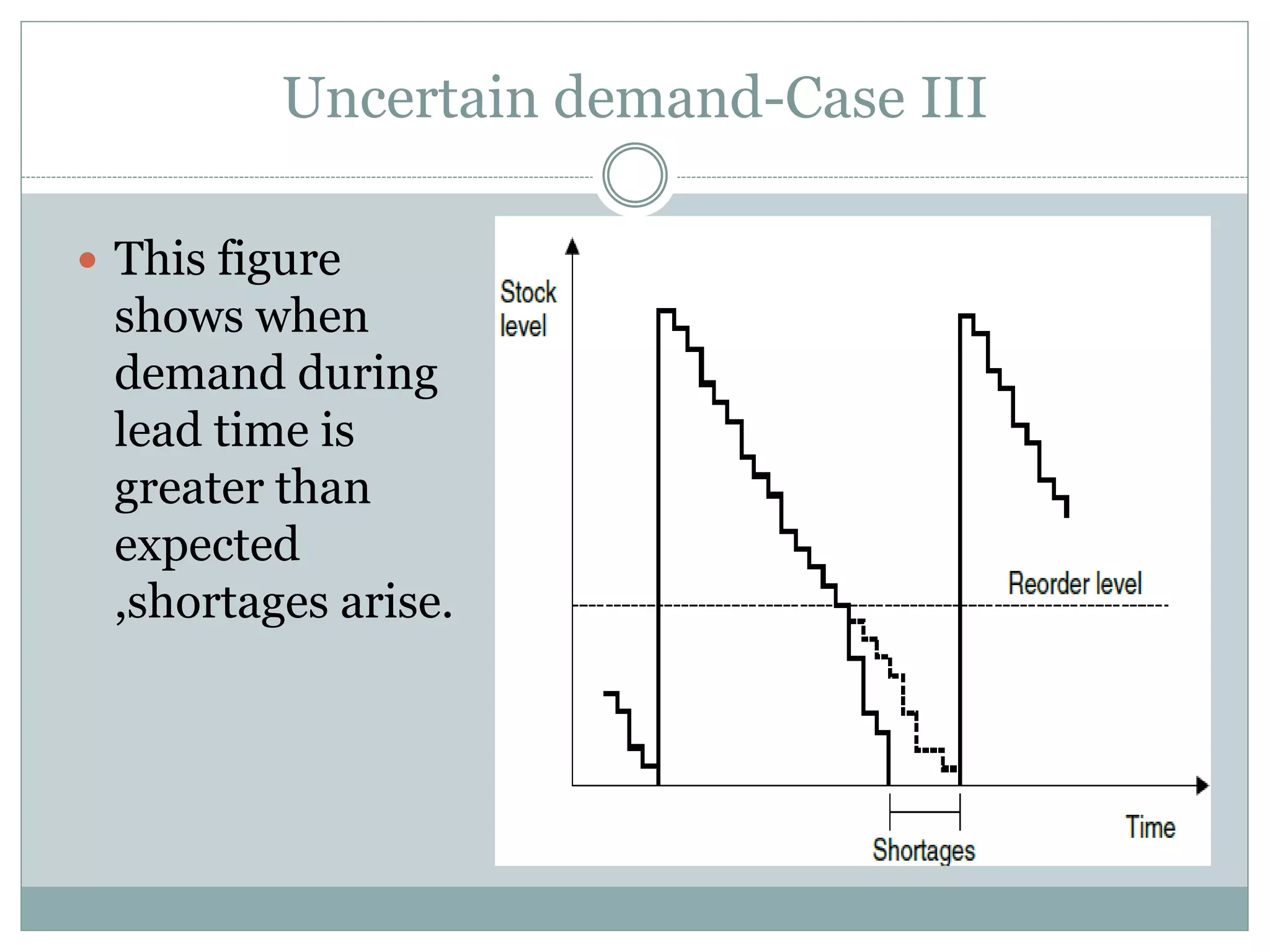
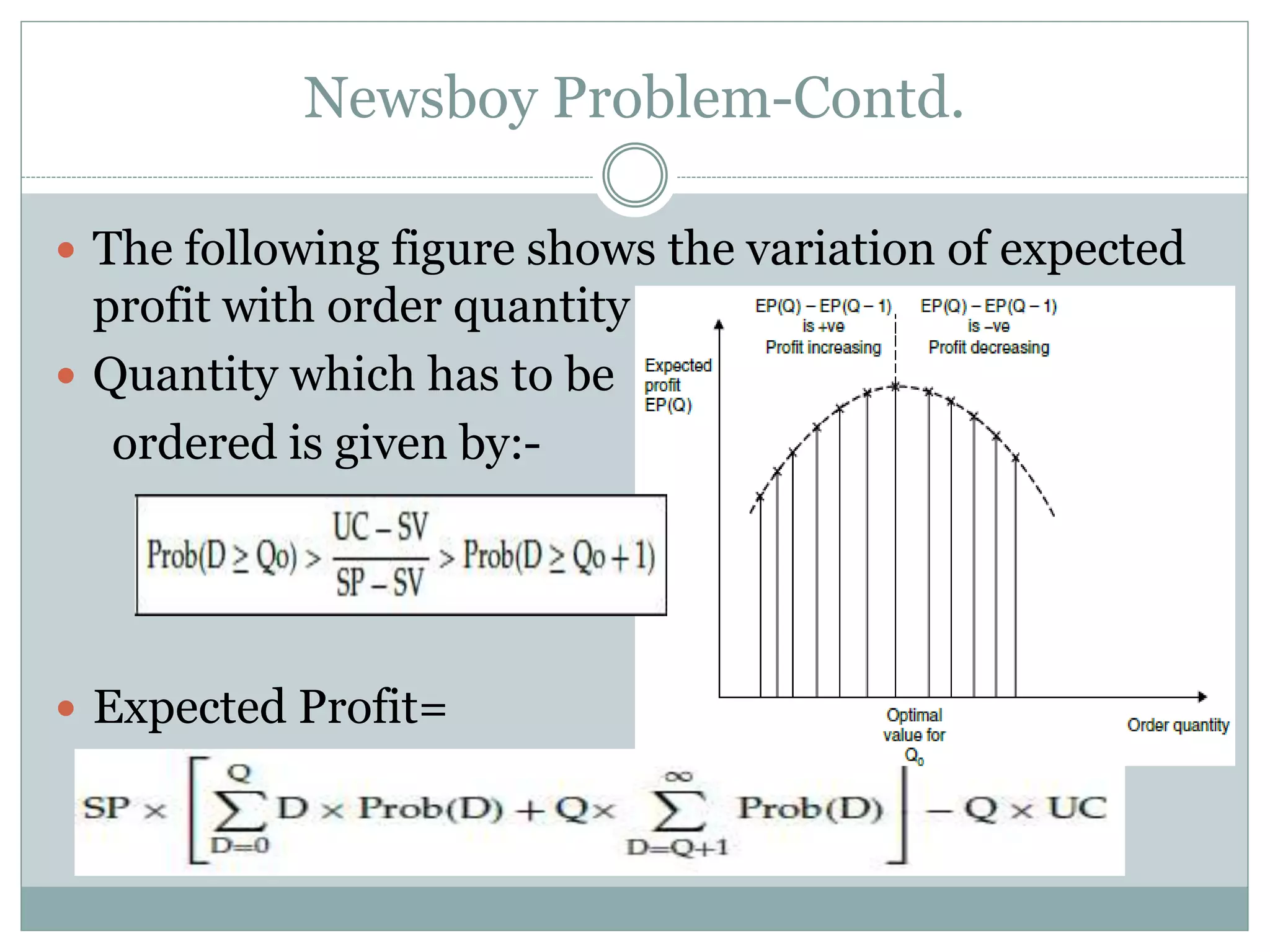
The document discusses various models for managing inventory and dealing with uncertainty in demand, costs, lead times, and other factors. It describes how uncertainty can be classified as unknown, known, or uncertain and probabilistic models can handle uncertain situations. Different cases of uncertain demand are illustrated, and models for discrete demand, the newsboy problem, shortages, intermittent demand, service level, and target stock levels are explained. Examples are provided to demonstrate how to determine optimal order quantities, safety stocks, reorder levels, and target inventory levels given uncertainty in demand and lead times.

1. Inventory Control and
Management

2. Uncertainty in stocks
 There Is always some uncertainty in stocks maybe because price
rise with inflation, operations change, supply chains are
disrupted and so on.
 The main uncertainty Is likely to be in customer demand which is
quite volatile.
 Problems can be classified according to following variables:-
 Unknown-in which we have complete ignorance of the situation
and any analysis is difficult
 Known- in which we know the values taken by parameters and
can use deterministic models.
 Uncertain-in which we have probability distributions for the
variables and can use probabilistic or stochastic models.

3. Uncertainty in other areas
 Demand – Demand for an item usually comes from a
number of separate customers.The organization has no
control over who buys their products and in what
quantity.These fluctuations in the number and size of
orders give an uncertain demand.
 Costs-costs tend to drift upwards with inflation. There can
be short term variations as well due to changes in
operations,products etc.
 Lead Time- Lead time is prone to variability as well which
is inevitable as it involves many stages between the decision
to buy an item and having it available for use.
 Deliveries- deliveries ultimately depend on supplier
reliability. They can fluctuate due to rejection during
quality checks,overage etc.

4. Uncertain demand-Case I
 This figure shows
the case when
actual demand
during lead time
matches expected
demand.

5. Uncertain Demand-Case II
 This figure shows
when demand
during lead time
is less than
expected, it leads
to unused stock.

6. Uncertain demand-Case III
 This figure
shows when
demand during
lead time is
greater than
expected
,shortages arise.

7. Models for discrete demand
 If the demand is discrete, and we place a very small order
for Q units the probability of selling the Qth unit is high
and expected profit is greater than expected loss.
 If a large order is placed the probability of selling Qth
unit is low and the expected profit is less than the
expected loss. Which leads us to the conclusion that best
order size is the quantity which gives a profit on Qth unit
and a loss on (Q+1)th and following units and any units
unsold will be sold at their scrap value.
 General rule to place an order for the largest value of Q is
given by :-

8. Example

9. Example-Contd.

10. Newsboy Problem
 Marginal analysis is useful for seasonal goods and a
standard example is of a newsboy selling papers on a
street corner. He has to decide how many papers to
buy from his supplier when customer demand is
uncertain.
 If too many papers are bought he will be left with
unsold stock which has no value and if too few
papers are bought he will be devoid of higher profit.
 The total expected profit from buying Q newspapers
is the sum of the profits multiplied by their
probabilities.

11. Newsboy Problem-Contd.
 The following figure shows the variation of expected
profit with order quantity
 Quantity which has to be
ordered is given by:-
 Expected Profit=

12. Example

13. Example-Contd.

14. Extension of Newsboy Problem
 An extension of newsboy problem is discrete demand
with shortages . This approach incorporates the scrap
value into a general shortage cost, SC.
 When an amount of stock A is greater than the demand D
there is a cost for holding units that are not used. (A-D) x
HC
 When demand D is greater than the stock A there is a
shortage cost for demand not met. (D-A) x SC
 And the total expected cost is given by :

15.  The same approach as the newsboy problem is
followed and the quantity is selected by this given
equation:-

 This is an example of the same:-

16. Example-Contd.

17. Intermittent Demand
 Many Organizations have a particular problem with
stocks of spare parts for equipments. These part may
be used rarely but have high storage costs that they
must remain in stock . Demand of this type is called
intermittent or lumpy with a typical pattern for
consecutive periods like
 0 0 10 0 0 0 0 0 25 0 0 0 0 0 0 0 0 0 5 0 0 0 0

18.  There are similar problems with components for
batch production. The materials needed in one
batch must be in stock when this batch is being
worked on , but then they are not needed for other
batches . The main problem is finding a reasonable
forecast . One approach is to consider separately:
 1: Expected no. of periods between demands , ET
 2: Expected size of a demand , ED

19.  Then the probability of a demand in any period is
1/ET, so we can forecast demand from : Forecast
Demand = ED/ET
 If we know the shortage cost we can balance this
against holding cost and calculate an optimal value
for A, the amount of stock that minimizes the
expected total cost . Alternatively , we can look at
the service level , with Service level = 1-
prob(shortage)
=1-[prob(there is demand)xProb(demand>A)]

20.  Where
Prob(there is demand)=1/ET
Prob(demand>A)can be found from the
distribution of demand
 This kind of problem is notoriously difficult and
the results are often reliable . In practice , the best
policy is often a simple rule along the lines of ‘order
a replacement unit whenever one is used’

21.  Example : Mean time between demands for spare part
is 5 weeks, and the mean demand size is 10 units . If
the demand size is normally dist. With Std. deviation of
3 units , what stock level would give a 95% service
level?
 Ans: we know that service level =
1-[Prob(there is demand)xProb(demand>A)] and we
want Prob(there is demand)xProb(demand>A)=.05
but Prob(there is demand) = 1/5 so Prob(demand>A)
= .05/2 =.25 for the norm. dist. This equals to 0.67 s.d
giving A=ED+Z.σ=10+0.67x3 =12units . This ans
makes assumptions but its reasonable

22. Order quantity with shortages
 Combining the model for variable,discrete demand
and a model which includes shortages. We arrive at a
new model Order quantity with shortages.
 Quantity is found using following equation

23. Steps Involved
1. Calculate the economic order quantity and use this
an initial estimate of Q.
2. Substitute this value for Q into the second equation
and solve this to fund a value for ROL.
3. Substitute this value for ROL into the first equation
to give a revised value for Q.
4. Repeat Steps 2 and 3 until the results converge to
their optimal values.

24. Example

26.  Conclusion:-the economic order quantity does not allow for
shortages so it tends to underestimate the optimal order
quantity. Adding a shortage cost gives more reliable results.

27. Service Level
 Organizations hold an extra reserve of stock knowing
that It will normally not be used but it is available
when deliveries are late or demand is higher than
expected. This reserve stock forms the safety stock.
 Service level is a target for the proportion of demand
that is met directly from stock – or alternatively, the
maximum acceptable probability that a demand
cannot be met from stock. A service level is usually
specified by the organization.

28.  Following figure shows how having a safety stock
adds a margin of security.

29. Example

30. Uncertain demand
 In case of uncertain demand the safety stock is found
out by the following equation.
 And, reorder level is given by.

31. Uncertain lead time
 Lead time is the time taken by the supplier to
actually deliver the goods. There can be quite
uncertainty in this lead time.
 service level in this case Is found out by the given
equation:-

32. Uncertainty in both lead time and demand
 There are times when there is uncertainty in both
lead time and demand as well. Then service level is
found by:-
where

33. Example

34. Example-Contd.

35. Target Stock Level
 There are two diff. approaches to ordering: fixed
order quantity methods , where we place an order of
fixed size whenever stock falls to a certain level; and
periodic review method, where we order varying
amount at regular intervals . Fixed order method
allows for uncertainty by placing orders of fixed size
at varying time intervals and vice versa for periodic
review method

36.  These two approaches are identical if demand is constant
, differences appear only when demand is uncertain .
 With periodic review method, the stock level is examined
at a specified time, and the amount needed to bring this
up to a target level is ordered .
 The order level T can be any convenient period . It might
be easiest to place an order at the end of every week, or
every morning, or at the end of a month

37.  A useful approach calculates an economic order quantity,
and then finds the period that gives orders of about this
size. The final decision is largely a matter for
management judgment.
 To find the target stock level we have to do some
calculations. We assume that lead time LT is const. and
demand is normally dist. The demand over T+LT is
normally dist. With mean of (T+LT)xD, Variance of
σ^2X(T+LT) and s.d of σx(T+LT)^.5 so we get

38.  Target Stock level = Mean demand over(T+LT) + Safety
Stock , We also know that Safety Stock=Z x S.D of
demand over T+LT = Z x σ x(T+LT)^.5
As usual Z is the no. of s.d from the mean corresponding
to the service level . So:Target Stock level =Dx(T+LT)+Zx
σ x(T+LT)^.5 this assumes that lead time is less than the
cycle length . If this is not true, the order also has to take
into account the stock already on order so that
Order quantity=Target stock level-Stock in hand-Stock in
order

39. Example
 Example: A management workshop explained demand for an item
is normally dist. With mean of 1000units a month and s.d of
100units. They check stock every three months and lead time is
const. at one month . They use an ordering policy that gives a 95%
service level, and wanted to know how much it would cost to raise it
to 98% if the holding cost is ₨20 a month .
Ans: listing the variables in consistent units D= 1000units a month
σ=100 units HC= Rs20 a unit a month T=3months LT=1month

40. Example-contd.
For 95% safety Z is 1.64 . Then Safety stock =
Zxσx(T+LT)^.5=1.64x100x(3+1)^.5 = 328 units
target stock level=Dx(T+LT)+Safety stock
=1000x(3+1)+328 = 4328 units , every three months
when it is time to place an order the company
examines the stock on hand and place an order for :
order size = 4328-stock on hand . The cost for holding
the safety stock =SSxHC= 328x20 = 6560 a month . If
the service level is increased to 98% Z=2.05
safety stock=2.05x100x4^.5 =410 , target stock level is
then 4410 units and the cost of the safety is 410x20 =
Rs8200 a month .