Rotating machines part 1

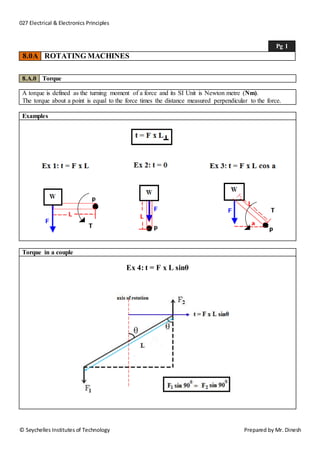
027 Electrical & Electronics Principles
Pg 1
8.0A ROTATING MACHINES
8.A.0 Torque
A torque is defined as the turning moment of a force and its SI Unit is Newton metre (Nm).
The torque about a point is equal to the force times the distance measured perpendicular to the force.
Examples
Torque in a couple
Ex 4: t = F x L sinθ
© Seychelles Institutes of Technology Prepared by Mr. Dinesh

Pg 2
8.A.1 Torque on a coil in a magnetic field
Fig 1
Fig 1 (a) is the field between two magnets, (b) the field due to a current in a straight wire and (c) the
resulting field if they are put together. This last field is known as the "catapult" field because it tends to
catapult the wire out of the field in the direction shown by the arrow.
Fig 2
Fig 2(a) show If a coil carrying a current is placed in a magnetic field it will experience a force on two
of its sides in such a way as to make the coil rotate.
Fig 2(b) shows coil will rotate from the 'double catapult' field diagram. Since the current moves along
the two opposite sides of the coil in opposite directions the two sides receive a force in opposite
directions also, thus turning the coil.

Pg 3
8.A.2 Torque on a current carrying conductor
Consider a rectangular coil in Fig 3 when the plane of the coil is lying along the field lines (θ = 90o)
Where, τ = torque (Nm)
L = length (m)
W = width (m)
B = magnetic field (Wb)
I = current (A)
Fig 3
τ = F x perpendicular distance
τ = F x W
= BIL x W
= BI(LW)
τ = BIA

Pg 4
Consider a number of rectangular coil in fig 4 when the plane of the coil is rotating along the field lines
Where, τ = torque (Nm)
L = length (m)
W = width (m)
d = perpendicular distance (m)
θ = angle (°)
I = current (A)
N = number of turns
Fig 4
τ = F x perpendicular distance
τ = F x d
= BILN x Wsinθ
= BI(LW)Nsinθ
τ = BIANsinθ

Pg 5
8.A.3 Solved work examples on “torque on a current carrying conductor”
Work example 1
Calculate the torque needed to hold a coil of 20 turns and area 8cm2 at an angle of 60o to a magnetic
field of flux density 0.1T if the coil carries a current of 0.5 A.
Solution
Torque, τ = BANIsinθ
= 0.1x20x8x10-4sin 60°
τ = 8x10-4 Nm
Work example 2
a) What is the maximum torque on a 150-turn square loop of wire 18.0 cm on a side that carries a 50.0A
current in a 1.60-T field?
b) What is the torque when θ is 10.9°?
Solution
a) Maximum torque, τ = BANIsinθ
= 1.60x150x0.0182 x50.0sin 90°
τ =
b) When θ is 10.9°, τ = BANIsinθ
= 1.60x150x0.182 x50.0sin 10.9°
τ =

Pg 6
8.A.4 E.m.f. induced in a straight conductor in a uniform magnetic field
When a straight conductor is moved through a magnetic field an e.m.f. is induced between its ends. This
movement must be in such a direction that the conductor cuts through the lines of magnetic flux, and
will be a maximum when it moves at right angles to the field (Fig 5).
Where, E = e.m.f. induced (V)
L = length (m)
v = velocity (m/s)
Fig 5
If the conductor moves with velocity v at right angles to the field then the flux cut per second will be
BvL (since the conductor will sweep out an area vL every second).
But the rate of cutting flux is equal to the e.m.f. induced in the conductor. Therefore
E = BLv

Pg 7
If the conductor cuts through the flux at an angle θ ( in Fig 5), where θ is the angle between the magnetic
field and the direction of motion, the equation becomes
E = BLv sinθ
8.A.5 Solved work examples on Emf induced on a straight conductor
Work example 1
Calculate
a) The e.m.f. generated between the wing tips of an aircraft that is flying horizontally at 200 ms-1 in a region
where the vertical component of the Earth's magnetic field is 4.0x10-5 T, if the aircraft has a wingspan of 25 m.
b) What will be the e.m.f. if the θ = 30°.
Solution
a) Maximum e.m.f., E = BLvsinθ
= 4.0x10-5x25x200 sin 90°
E = 0.2V
b) When θ is 30°, E = BANIsinθ
= 4.0x10-5x150x200 sin 30°
E = 0.1V

Pg 8
8.A.4 Emf induced in a straight conductor rotating in a uniform magnetic field
Consider the Fig 6, a diagram of an electrical generator. A generator with a single rectangular coil
rotated at constant angular velocity in a uniform magnetic field produces an e.m.f. that varies
sinusoidally in time. Note the generator is similar to a motor, except the shaft is rotated to produce a
current rather than the other way around.
Where, E = e.m.f. induced (V)
L = length (m)
v = velocity (m/s)
θ = angle (°)
ω = angular velocity (rad/s)
Fig 6
The induced e.m.f. by considering only the side wires.
Motional e.m.f. is given to be E = BLv, where the velocity v is perpendicular to the magnetic field B
Here, the velocity is at an angle θ with B, so that its component perpendicular to B is vsinθ.
Thus in this case the e.m.f. induced on each side is E = BLvsinθ, and they are in the same direction.
The total EMF ε around the loop is then: E = 2BLvsinθ
This expression is valid, but it does not give EMF as a function of time.

Pg 9
To find the time dependence of EMF, we assume the coil rotates at a constant angular velocity ω.
The angle θ is related to angular velocity by θ = ωt, so that: E = 2Blvsinωt
Now, linear velocity v is related to angular velocity by v = rω.
Here r = w/2, so that v = (w/2)ω, and:
E = 2BLw2ωsinωt
E = (Lw)Bωsinωt
Noting that the area of the loop is A = Lw, and allowing for N loops, we find that:
E = NABω sinωt
The maximum value of the e.m.f (Emax) is when θ (= ωt) = 90o, is given by
E = NABω

Pg 10
8.A.5 Solved work examples on Emf induced in a rotating in a uniform magnetic field
Work example 1
Calculate
a) The maximum value of the e.m.f generated in a coil with 200 turns and of area 10 cm2 rotating at 60
radians per second in a field of flux density 0.1 T.
b) The e.m.f. when θ = 60o
Solution
a) Maximum e.m.f., E = BANωsinθ
= 0.1x10-5x200x60 sin 90°
E = 1.2V
b) When θ is 30°, E = BANωsinθ
= 0.1x10-5x200x60 sin 60°
E = 1.04V
Notice the use of radians per second.

Pg 11
8.A.6 Power generated in rotating machines
The linear motion of a conductor through a magnetic field, the mechanical power supplied is equal to
the electrical power generated.
8.1.7 Derivation of power in rotating machines
For a rotating object, the linear distance covered at the circumference of rotation is the product of the
radius with the angle covered.
That is:
Linear distance = radius × angular distance.
By definition,
Linear distance = linear speed × time = radius × angular speed × time.
By the definition of torque:
Torque = radius × force.
These two values can be substituted into the definition of power:
Power = Force × Linear distance
Time
= (Torque⁄Radius)× (Radius × Angular speed)
Time
= Torque × Angular speed
or
Power = Torque × 2π × Rotational speed
Where, Torque, τ (N/m)
Angular speed, ω (rad/s)
Rotational speed, n (rev/s)
Radius, r (m)

Pg 12
Rotational power is given by,
P = ω. τ
Where, ω, angular velocity is defined as the rate of change of angular displacement which
specifies the angular speed (rotational speed) of an object and the axis about which the
object is rotating. Measured in radian per second (rad/s)
τ, torque is defined as the moment of force is the tendency of a force to rotate an object
about an axis. Measured in newton per metre (N/m)
P, In rotational systems, power is defined as the product of the torque and angular
velocity. Measured in watts (W)
8.A.8 Power efficiency
Power efficiency is defined as the ratio of output power divided by input power.
Ƞ = 100% ·
Where, ƞ = efficiency (%)
Pout = output power (W)
Pin = input power (W)
퐏퐨퐮퐭
퐏퐢퐧

Pg 13
8.A.9 Solved work examples on power in rotating machines
Work example 1
A machine is rotating with speed of 3000 rev/min (rpm) consumes 5kW. Calculate the torque of the
shaft.
Solution
Given, ƞ = 3000 rpm
P = 5kW
τ = ?
Using τ = 퐏/ퟐ훑ƞ
= (5 × 1000) ÷ [(2π ×
3000
60
)]
τ = 15.9 N/m
Work example 2
An electric motor has an input power consumption of 50 watts. The motor was activated for 60 seconds
and produced work of 2970 joules. Find the efficiency of motor?
Solution
Given, Pin = 50W
t = 60s
E = 2970J
ƞ = ?
Pout = ?
Using Pout = E / t
= 2970/60
Pout = 49.45W
Now ƞ = ퟏퟎퟎ% × 퐏퐨퐮퐭 / 퐏퐢퐧
= ퟏퟎퟎ × (ퟒퟗ. ퟗퟓ/ퟓퟎ)
ƞ = ퟗퟗ%

Rotating machines part 1

Recommended

Recommended

More Related Content

What's hot

What's hot (18)

Similar to Rotating machines part 1

Similar to Rotating machines part 1 (20)

Recently uploaded

Recently uploaded (20)

Rotating machines part 1