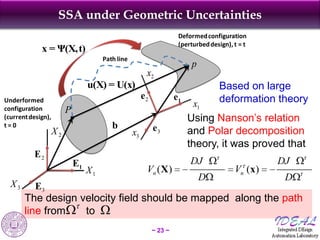
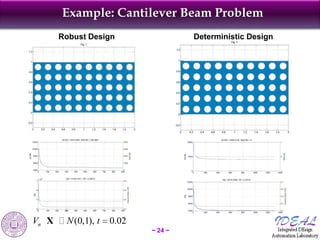
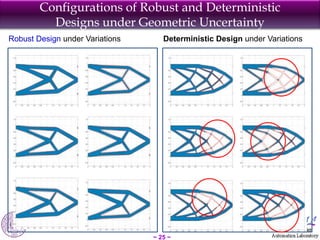
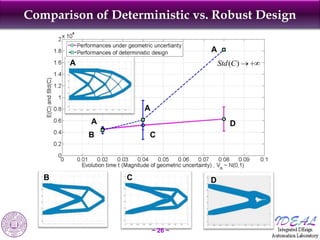
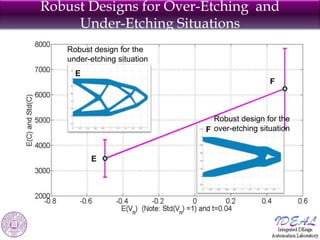
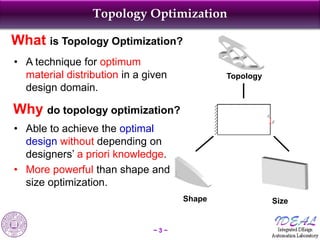
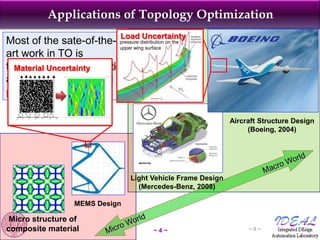
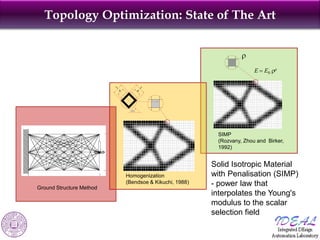
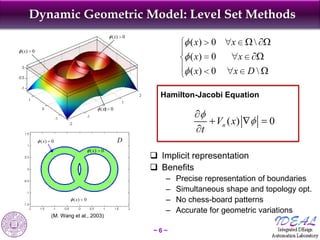
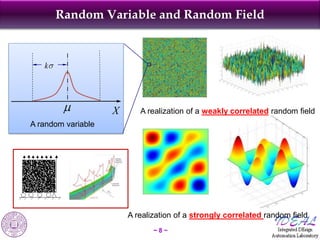
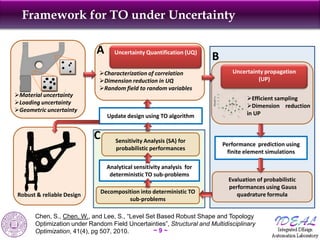
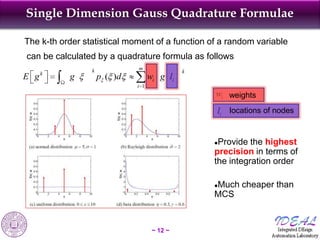
The document discusses robust shape and topology optimization under uncertainty, focusing on advanced techniques like level set methods and challenges related to load, material, and geometric uncertainties. It outlines a rigorous framework for implementing robust optimization and presents applications and examples, including the optimization of aircraft structures and microgrippers. The content emphasizes the significance of addressing uncertainties in the design process to enhance robustness and reliability in engineering designs.

1. McCormick School of Engineering
Northwestern University
Robust Shape &Topology
Optimization under Uncertainty
Prof. Wei Chen
Wilson-Cook Professor in Engineering Design
Integrated DEsign Automation Laboratory (IDEAL)
Department of Mechanical Engineering
Northwestern University
Based on Shikui Chen’s PhD Dissertation
http://ideal.mech.northwestern.edu/

2. Presentation Outline
1. Topology Optimization
 Level set method
 Challenge for topology optimization under uncertainty
2. Robust Shape and Topology Optimization (RSTO)
 Framework for RSTO
 RSTO under Load and Material Uncertainties
 RSTO under Geometric Uncertainty
3. Examples
4. Conclusion

3. Topology Optimization
What is Topology Optimization?
• A technique for optimum
material distribution in a given Topology
design domain.
Why do topology optimization?
• Able to achieve the optimal
design without depending on
designers’ a priori knowledge.
• More powerful than shape and
size optimization.
Shape Size
~3~

4. Applications of Topology Optimization
Load Uncertainty
Most of the sate-of-the- pressure distribution on the
upper wing surface
art work in TO is
focused Uncertainty
Material on deterministic
and purely mechanical
problems.
Aircraft Structure Design
(Boeing, 2004)
Light Vehicle Frame Design
(Mercedes-Benz, 2008)
MEMS Design
Micro structure of
composite material ~4~ ~4~

5. Topology Optimization: State of The Art
E E0 p
SIMP
(Rozvany, Zhou and Birker,
1992)
Solid Isotropic Material
Homogenization with Penalisation (SIMP)
(Bendsoe & Kikuchi, 1988) - power law that
Ground Structure Method
interpolates the Young's
modulus to the scalar
selection field

6. Dynamic Geometric Model: Level Set Methods
( x) 0
( x) 0 x
( x) 0
( x) 0 x
( x) 0 x D
Hamilton-Jacobi Equation
( x) 0
Vn ( x) 0
t
( x) 0 D
( x) 0
 Implicit representation
 Benefits
– Precise representation of boundaries
– Simultaneous shape and topology opt.
( x) 0 – No chess-board patterns
– Accurate for geometric variations
(M. Wang et al., 2003)
~6~

7. Formulation for Robust Shape and Topology
Optimization
f (X) Minimize
minimize [ f , f ] J * ( , u, z ) ( J ( , u, z )) k ( J ( , u, z )
s.t. g k g 0 Subject to :
Volume constraint obj
,
Perimeter constraint on ,
divσ (u) f in
robust X
u 0 on D
Robust Design Model (Chen, 1996) σ (u) n g on N
Challenges in RSTO:
• Modeling and propagation of high-dimensional
random-field uncertainty
• Sensitivity analysis for probabilistic
performances
~7~

8. Random Variable and Random Field
k
X A realization of a weakly correlated random field
A random variable
A realization of a strongly correlated random field
~8~

9. Framework for TO under Uncertainty
A Uncertainty Quantification (UQ)
B
Characterization of correlation Uncertainty propagation
Dimension reduction in UQ (UP)
Random field to random variables
Material uncertainty
Efficient sampling
Loading uncertainty
Dimension reduction
Geometric uncertainty
Update design using TO algorithm in UP
C Sensitivity Analysis (SA) for
Performance prediction using
probabilistic performances
finite element simulations
Analytical sensitivity analysis for
deterministic TO sub-problems
Evaluation of probabilistic
performances using Gauss
Decomposition into deterministic TO quadrature formula
Robust & reliable Design
sub-problems
Chen, S., Chen, W., and Lee, S., “Level Set Based Robust Shape and Topology
Optimization under Random Field Uncertainties”, Structural and Multidisciplinary
Optimization, 41(4), pg 507, 2010. ~9~

10. Module A: Uncertainty Representation
•Karhunen-Loeve Expansion
•A spectral approach to represent a random field using eigenfunctions
of the random field’s covariance function as expansion bases.
Random
ξ: orthogonal random parameters
Field
g mean function
:
ith eigenvalue ith eigenvector
x - spatial
coordinate
Significance check
- random Select M when s is close to 1
parameter
•Truncated K-L Expansion
Ghanem and Spanos 1991; Haldar and Mahadevan 2000; Ghanem and Doostan 2006
~ 10 ~

11. Module B: Uncertainty Propagation
Numerical Integration with Gaussian Quadrature Formula
Approximate the integration of a function g(ξ) by a weighted sum of
function values at specified points
Univariate Dimension Reduction (UDR) Method (Raman and
Xu, 2004)
• Approximate a multivariate function by a sum of multiple univariate functions
• Accurate if interactions of random variables ξ are relatively small
• Greatly reduce sample points for calculating statistical moments
~ 11 ~

12. Single Dimension Gauss Quadrature Formulae
The k-th order statistical moment of a function of a random variable
can be calculated by a quadrature formula as follows
k m
k k
E g g p ( )d wi g li
i 1
wi weights
li locations of nodes
Provide the highest
precision in terms of
the integration order
Much cheaper than

MCS
~ 12 ~

13. Tensor Product Quadrature vs. Univariate
Dimension Reduction
Tensor Product Quadrature UDR
x2 x2
1 1 1
36 9 36
1 4 1
9 9 9
x1 x1
1 1 1
36 9 36
mi
wi j weights yi wi j g X1 , , li j , Xn
j 1
1
li j location of mi 2 2
nodes yi wi j g X1 , , li j , , Xn g_ i
j 1
~ 13 ~

14. Module C: Shape Sensitivity Analysis for
Probabilistic Performances
Expand the functions of mean and variance using UDR in an additive
format n
D J D J_i n 1 D J , u, μ z (1)
i 1
n
1 2
D J D J_i (2)
n
2 i 1
J_i
i 1
Using adjoint variable method and shape sensitivity analysis (Sokolowski,
1992),we can calculate (1) and (2), and further obtain
D J * ( , u, z ) D ( J ( , u, z )) kD ( J ( , u, z))
n n
k
D J_i n 1 D J ( , u, μ z ) D 2
J_i
n
i 1 2 i 1
J_i
i 1
J* u Vn ds Steepest Descent Vn u t Vn | | 0
~ 14 ~

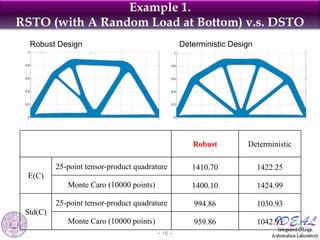
15. Example 1. Bridge Beam with A Random Load at Bottom
(1) RSTO under loading uncertainty (2) Deterministic Topology Optimization
f f
Angle: Uniform distribution [-3pi/4, -pi/4],
Domain size: 2 by 1 , f 1
magnitude: Gumbel distribution (1, 0.3)
~ 15 ~

16. Example 1.
RSTO (with A Random Load at Bottom) v.s. DSTO
Robust Design Deterministic Design
Robust Deterministic
25-point tensor-product quadrature 1410.70 1422.25
E(C)
Monte Caro (10000 points) 1400.10 1424.99
25-point tensor-product quadrature 994.86 1030.93
Std(C)
Monte Caro (10000 points) 959.86 1042.93
~ 16 ~

17. Example 2
A Micro Gripper under A Random Material Field
1
f out
f in
2
f out
Chen, S., Chen, W., and Lee, S., 2010, "Level set based robust shape and topology optimization
under random field uncertainties," Structural and Multidisciplinary Optimization, 41(4), pp. 507-
524. ~ 17 ~

18. Example 2
Robust Design vs. Deterministic Design
Parameters Volume Ratio Robust Design Deterministic
Design
Material Field 1 E 1 0.090 -0.065 -0.07
Material Field 2 E 1 0.098 -0.059 -0.055
E 0.3
d 0.5
~ 18 ~

19. Geometric Uncertainty Modeling with A Level Set Model
 Represents geometric
uncertainty by modeling the
normal velocity field as a
random field;
 Naturally describes topological
changes in the boundary
perturbation process;
 Can model not only uniformly too
thin (eroded) or too thick (dilated)
structures but also shape-
dependent geometric uncertainty
Eulerian d ( X)
Vn ( X, z ) ( X) 0
Description dt
Chen, S. and Chen, W., “A New Level-Set Based Approach to Shape and
Topology Optimization under Geometric Uncertainty”, Structural and
Multidisciplinary Optimization, 44, 1-18, April 2011
~ 19 ~

20. Module A: Geometric Uncertainty
Quantification
Extracted boundary points from the
level set model N
a x, a x i ai x i
~ 20 ~ i 1

21. Extending Boundary Velocity to The Whole
Design Domain
Vn
sign( ) V 0
Initial velocity on the boundary Extended velocity on the whole domain
d (X )
Vn ( X , z) (X ) 0
dt
~ 21 ~

22. Challenges in Shape Sensitivity Analysis under Geometric
Uncertainty
Conventional SSA Problem : How to
change to minimize J
DJ
D
Our problem: Need shape gradient
of J and J at the same
time
Challenge: Need shape gradient of J
DJ
is with respect to Vn
D
~ 22 ~

23. SSA under Geometric Uncertainties
Deformed configuration
(perturbed design), t = t
x = Ψ(X,t)
Path line
p
x2
u(X) = U(x) Based on large
Underformed
e2 e1 deformation theory
configuration
x1
P
(current design), Using Nanson’s relation
t=0 b e3
X2 x3 and Polar decomposition
theory, it was proved that
E2
E1 DJ DJ
X1 Vn ( X ) Vn (x)
D D
X3 E3
The design velocity field should be mapped along the path
line from to
~ 23 ~

24. Example: Cantilever Beam Problem
Robust Design Deterministic Design
Vn X N (0,1), t 0.02
~ 24 ~

25. Configurations of Robust and Deterministic
Designs under Geometric Uncertainty
Robust Design under Variations Deterministic Design under Variations
~ 25 ~

26. Comparison of Deterministic vs. Robust Design
A
A Std (C )
A
A D
B C
B C D
~ 26 ~

27. Robust Designs for Over-Etching and
Under-Etching Situations
Robust design for the
under-etching situation
E
F
Robust design for the
F over-etching situation
E

28. Summary
 Demonstrated the importance of considering
uncertainty in topology optimization
 A unified, mathematically rigorous and
computationally efficient framework to
implement RSTO
 First attempt of level-set based TO under
geometric uncertainty (TOGU)
 Bridge the gap between TO and state-of-the
art techniques for design under uncertainty
~ 28 ~