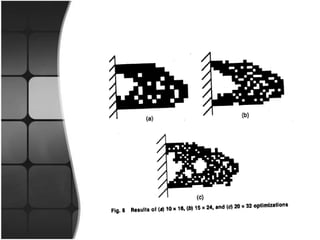
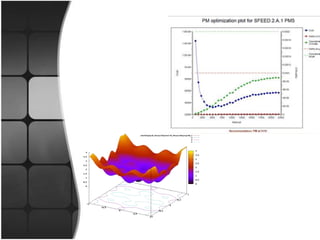
This document discusses topology optimization. It begins by defining topology and optimization separately, then explains that topology optimization is a mathematical approach that optimizes material layout within a design space to meet performance targets while minimizing a given objective like mass or deflection. It provides an example of using topology optimization on a cantilever beam by dividing it into elements, removing less stressed elements through iterations, analyzing the results, and continuing until the objective is met. Finally, it mentions software tools used in the topology optimization process and some applications.

1. Topology Optimization
P Venkat Vijay Kumar
Mechanical branch
KLUniversity

2. What is Topology???
Topology is a major area of mathematics
concerned with properties that are preserved
under continuous deformations of objects,
such as deformations that involve stretching,
but no tearing or gluing

4. Then… Optimization???
In mathematics, computational science, or
management science, mathematical optimization
(alternatively, optimization or mathematical
programming) refers to the selection of a best
element from some set of available alternatives.

6. Finally… Topology Optimization
Topology optimization is a mathematical
approach that optimizes material layout
within a given design space, for a given set of
loads and boundary conditions such that the
resulting layout meets a prescribed set of
performance targets.

8. How???
• Any optimization technique can be used as
tool of optimization in Topology Optimization.
• An objective function has to be formulated
which has to be optimized / maximized /
minimized.
• Then using the optimization techniques
number of probabilities are produced and the
result that suits best is choosen.

9. Detailed how????
• Lets start with little more detail.
• Consider a structure or component, say a
cantilever beam. Let our objective be
minimizing the deflection if possible,
minimizing the mass
Cantilever beam
Load F

10. Original deflections and stresses in the beam in the
initial conditions of load and structure

11. Divide the cantilever
into number of
1 1 1 1 1 1 1 1 1 1
checks i.e. rows 1 1 1 1 1 1 1
Cantilever beam
1 1 1
1 1 1 1 1 1 1 1 1 1
and columns. 1 1 1 1 1 1 1 1 1 1
Now, considering the presence of
material as 1 and void as 0, number
the checks one by one

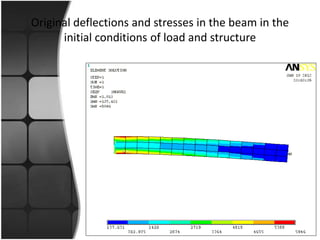
12. • Now would be the task of optimization.
• The numbers considered are taken into a row
matrix
[1 1 1 .. .. .. 40 1’s]
• From the original analysis its clear that some
portion of the beam is not taking the load,
therefore lets remove the portion with less
stress.

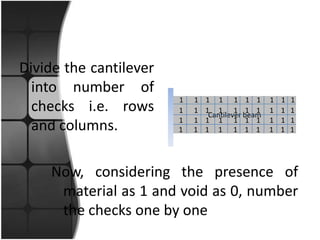
13. 1 1 1 1 1 1 1 1 1 1
0 0 0 1 1 1 1 1 1 1
Cantilever beam
0 0 0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
[1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 0 1
1 1 1 1 1 1 1 1 1 1 1 1 1]
- A parent

14. 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 1 1 1
Cantilever beam
0 0 0 0 0 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1
[1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 0
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
- One more parent

15. • For each parent we analyze the amount of
mass and deflection that occurs
• And keep doing until our objective is met.
• A topology optimized cantilever beam is as
follows…

17. Software… soft procedure
• Modeling
• Analysis
• Optimizing
• Remodeling
• Producing manufacturable design

18. Applications
• Now Topology optimization is
being spread to composite
structures
• Topology optimization is the major
tool for optimizing aero structures
• There are lot of things around us
that have to be optimized… ..