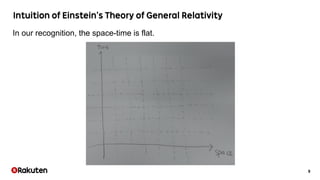
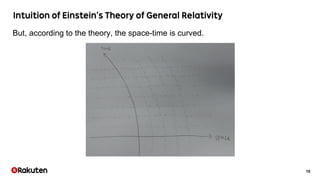
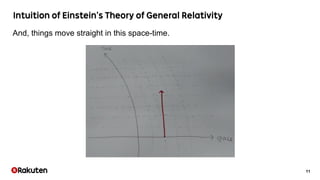
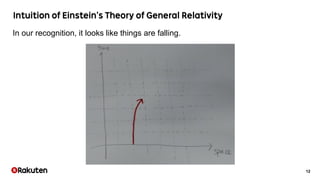
The document discusses the development of the Egison programming language aimed at representing algorithms and mathematical physics calculations. It highlights the challenges of representing curved spaces and curvature in four-dimensional time-space, along with the application of pattern-matching and tensor index notation for symbolic computation. The author is working towards effectively representing differential forms and operators in Egison, which can be applied in various fields like mathematics and physics.

1. v1 Oct.28.2017
Satoshi Egi
Rakuten Institute of Technology
Rakuten, Inc.

2. 2

3. 3
My aim is to create a language that can represent directly all algorithms that can be
discovered.
Currently, my biggest challenge is to improve Egison in order to represent directly
calculations that appear in mathematical physics.

4. 4
Pattern-matching against the wider range of data types.
Customizable symbolic computation using Egison pattern-matching.
Tensor index notation in programming.

5. 5
https://www.egison.org/math

6. 6
https://www.egison.org/math

7. 7
The theory for investigating a curved space.
It is easy for us in the 3 dimensional space to recognize a 2 dimensional curved
surface is curved.
How about our world? Is it curved for who can recognize the higher dimensional
space?
https://commons.wikimedia.org/wiki/File:Trian
gles_(spherical_geometry).jpg

8. 8
The theory explains the gravity as the curve of 4 dimensional time-space.
https://commons.wikimedia.org/wiki/File:Spacetime_lattice_analogy.svg

9. 9
In our recognition, the space-time is flat.

10. 10
But, according to the theory, the space-time is curved.

11. 11
And, things move straight in this space-time.

12. 12
In our recognition, it looks like things are falling.

13. 13
Formulas in Riemannian geometry are represented with partial derivative
operator and tensor index notation.
We can represent both of them concisely in Egison!

14. 14
Egison program that represents the above formula
Formula of Riemann curvature tensor
~: superscript
_: subscript

15. 15
Pattern-matching against the wider range of data types.
Customizable symbolic computation using Egison pattern-matching.
Tensor index notation in programming.

16. 16
Pattern-matching against the wider range of data types.
Customizable symbolic computation using Egison pattern-matching.
Tensor index notation in programming.

17. 17
Pattern Body
Matcher
Target

18. 18
are patterns.

19. 19
Pattern-matching against the wider range of data types.
Customizable symbolic computation using Egison pattern-matching.
Tensor index notation in programming.

20. 20

21. 21
We can apply Egison pattern-matching
against math expressions.
Math expressions are a multiset of terms.
Terms are a multiset of factors.
Therefore, Egison pattern-matching is
very useful to handle them.

22. 22
Pattern-matching against the wider range of data types.
Customizable symbolic computation using Egison pattern-matching.
Tensor index notation in programming.

23. 23
Tensor index notation is a popular notation in the field of mathematics and physics.

24. 24
We can control the way for multiplying vectors by indices.

25. 25
We can use tensor index notation to multiply any order of tensors.
The tensor index notation is necessary to represent the multiplication of order
tensors higher than matrices.

26. 26
In Egison method, we can apply directly both “∂/∂” and “.” functions to tensors.
Egison program that represents the above formula
Formula of Riemann curvature tensor
~: superscript
_: subscript

27. 27
Wolfram program that represents the above formula
Egison program that represents the above formula
Formula of Riemann curvature tensor

28. 28https://arxiv.org/abs/1702.06343

29. 29

30. 30
https://commons.wikimedia.org/wiki/File:T
riangles_(spherical_geometry).jpg

31. 31

32. 32

33. 33

34. 34

35. 35

36. 36

37. 37
https://commons.wikimedia.org/wiki/File:Spacetime_lattice_analogy.svg

38. 38

39. 39
Currently, I am working to represent differential forms, exterior derivative, and
Hodge operator directly in Egison.
If we realize that, there are the wide range of application, e.g. mathematics,
physics, and computer simulation.