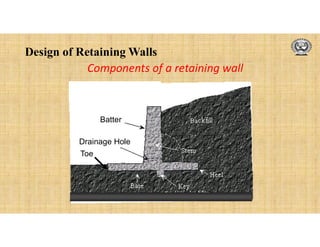
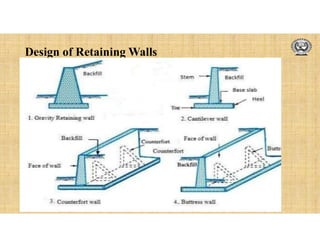
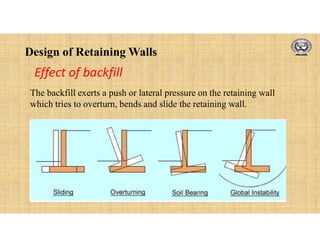
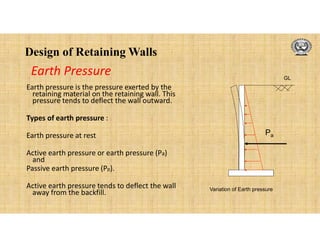
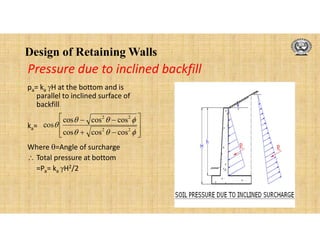
The document discusses the design of retaining walls. It defines a retaining wall as a structure used to hold back soil or other material at different levels on either side. It describes common types of retaining walls like gravity, cantilever, counterfort and buttress walls. Factors that influence the design are also discussed, including earth pressure, types of backfill, surcharge loads and drainage. The design process involves checking stability against overturning, sliding and bearing capacity failure. Reinforcement details and curtailment are also covered.

1. Design of Retaining Walls

2. Design of Retaining Walls
Retaining walls are usually
built to hold back soil
mass. However, retaining
walls can also be constructed
for aesthetic landscaping
purposes.
Retaining wall is a structure
used for maintaining the
ground surfaces at different
elevations on either side of it.
What is a Retaining wall?

3. Design of Retaining Walls
What is the use of a Retaining wall?

4. Design of Retaining Walls

5. Design of Retaining Walls

6. Design of Retaining Walls

7. Design of Retaining Walls
Components of a retaining wall
Batter
Drainage Hole
Toe

8. Design of Retaining Walls
•1. Gravity Retaining Walls /Semi-Gravity
Retaining Walls
•2. Cantilever Retaining Walls (L or T shape)
•3. Counter fort Retaining Walls
•4. Buttress Retaining wall
Types of retaining wall

9. Design of Retaining Walls

10. Design of Retaining Walls
• The “gravity wall” provides stability by
virtue of its own weight , and therefore, is
rather massive in size.
• It is usually built in stone masonry, and
occasionally in plain concrete
 The thickness of wall is also governed by
need to eliminate or limit the resulting
tensile stress to its permissible limit .
 Plain concrete gravity walls are not used
for heights exceeding about 3m, for
obvious economic reasons.
 Stress developed is very low.
 These walls are so proportioned that no
tension is developed anywhere and the
resultant of forces remain within the
middle third of the base.
Gravity retaining wall

11. Design of Retaining Walls
Cantilever retaining wall
 Concrete cantilever wall is an example and consists of a
reinforced concrete stem and a base footing.
 These walls are non-proprietary.
 The “Cantilever wall ” is the most common type of
retaining structure and is generally economical for heights
up to about 8m.
 The structure consists of vertical stem , and a base slab,
made up of two distinct regions, viz., a heel slab and a
toe slab
 “Stem” acts as a vertical cantilever under the lateral earth
pressure
 “Heel slab” acts as a horizontal cantilever under the action
of weight of the retained earth (minus soil pressure
acting upwards from below)
 “Toe slab ” acts as a cantilever under the action of
resulting soil pressure acting upward.
 It resists the horizontal earth pressure as well as other
vertical pressure by way of bending of various components
acting as cantilevers.
 May be L shaped or T shaped.

12. Design of Retaining Walls
 Stem and Heel slab are strengthened by
providing counterforts at some suitable intervals.
 The stability of the wall is maintained essentially
by the weight of the earth on the heel slab plus
the self weight of the structure.
 Counterfort wall are placed at regular intervals of
about1/3 to ½ of the wall height, interconnecting
the stem with the heel slab
 The counterforts are concealed within the
retained earth on the rear side of the wall.
 This wall is economical for heights above
(approximately) 7m.
 The counterforts subdivide the vertical slab
(stem) into rectangular panels and support them
on two sides(suspender-style), and themselves
behave essentially as vertical cantilever beams of
T-section and varying depth.
Counterfort Retaining wall

13. Design of Retaining Walls
• Backfill
• The material retained is known as Backfill
• Surcharge
• The backfill above the level of the top of the wall
• Inclined surcharge
• The sloping backfill is termed as Inclined surcharge
• Earth Pressure
• The pressure on the wall due to backfill
Terminology

14. Design of Retaining Walls
Effect of backfill
The backfill exerts a push or lateral pressure on the retaining wall
which tries to overturn, bends and slide the retaining wall.

15. Design of Retaining Walls
Earth pressure is the pressure exerted by the
retaining material on the retaining wall. This
pressure tends to deflect the wall outward.
Types of earth pressure :
Earth pressure at rest
Active earth pressure or earth pressure (Pa)
and
Passive earth pressure (Pp).
Active earth pressure tends to deflect the wall
away from the backfill.
Earth Pressure
Pa
GL
Variation of Earth pressure

16. Design of Retaining Walls
Earth Pressure at rest
When the soil behind the wall is prevented from lateral
movement (towards or away from soil) of wall, the
pressure is known as earth pressure at rest.
This is the case when wall has a considerable rigidity.
Basement walls generally fall in this category.

17. Design of Retaining Walls
If a retaining wall is allowed to move away
from the soil accompanied by a lateral soil
expansion, the earth pressure decreases
with the increasing expansion.
A shear failure of the soil is resulted with
any further expansion and a sliding wedge
tends to move forward and downward.
The earth pressure associated with this
state of failure is the minimum pressure
and is known as active earth pressure.
Active Earth Pressure Passive Earth Pressure
If a retaining wall is allowed to move
towards the soil accompanied by a lateral
soil compression, the earth pressure
increase with the increasing compression
in the soil.

18. Design of Retaining Walls
Earth pressure depends on
• type of backfill
• the height of wall and
• the soil conditions
Soil conditions: The different soil conditions are
• Dry leveled back fill
• Moist leveled backfill
• Submerged leveled backfill
• Leveled backfill with uniform surcharge
• Backfill with sloping surface
Factors affecting Earth Pressure

19. Design of Retaining Walls
Computation of Bending Moment and Shear Force
Maximum pressure at any height, p=kah
Total pressure at any height from top,
pa=1/2[kah]h = [kah2]/2
Bending moment at any height
M=paxh/3= [kah3]/6
 Total pressure, Pa= [kaH2]/2
Total Bending moment at bottom,
M = [kaH3]/6
Pa
H
h
kaH
M

20. Design of Retaining Walls
Where, ka= Coefficient of active earth pressure
= (1-sin)/(1+sin)=tan2
= 1/kp, coefficient of passive earth pressure
= Angle of internal friction or angle of repose
=Unit weigh or density of backfill
If = 30, ka=1/3 and kp=3. Thus ka is 9 times kp

21. Design of Retaining Walls
Pressure due to inclined backfill
pa= ka H at the bottom and is
parallel to inclined surface of
backfill
ka=
Where =Angle of surcharge
 Total pressure at bottom
=Pa= ka H2/2


















 2
2
2
2
cos
cos
cos
cos
cos
cos
cos

22. Design of Retaining Walls
Design Requirements for Retaining wall
Following conditions must be satisfied for stability of wall (IS:456-2000).
• It should not overturn
• It should not slide
• It should not subside, i.e Max. pressure at the toe should not exceed the
safe bearing capacity of the soil under working condition

23. Design of Retaining Walls
Factor of safety against overturning
= MR / MO  1.55 (=1.4/0.9)
Where,
MR =Stabilising moment or restoring
moment
MO =overturning moment
As per IS:456-2000,
MR>1.2 MO, ch. DL + 1.4 MO, ch. IL
0.9 MR  1.4 MO, ch IL
Check against Overturning

24. Design of Retaining Walls
FOS against sliding
= Resisting force to sliding/
Horizontal force causing
sliding
= W/Pa  1.55 (=1.4/0.9)
As per IS:456:2000
1.4 = ( 0.9W)/Pa
Check against Sliding
Friction  W
SLIDING OF WALL

25. Design of Retaining Walls
=45 + /2
a
pp
R
A
B

W ka(H+a)
PA
H+a
H
C
In case the wall is unsafe against
sliding
pp= p tan2 (45 +/2)
= p kp
where pp= Unit passive pressure on
soil above shearing plane AB
p= Earth pressure at BC
R=Total passive resistance=ppxa
Design of Shear Key

26. Design of Retaining Walls
If W= Total vertical force acting at the key base
= shearing angle of passive resistance
R= Total passive force = pp x a
PA=Active horizontal pressure at key base for H+a
W=Total frictional force under flat base
For equilibrium, R + W =FOS x PA
FOS= (R + W)/ PA  1.55
Design of Shear Key …contd

27. Design of Retaining Walls
T
x1
x2
W1
W2
W3
W4
b/2
b/6
e
x
b
H/3
Pa
W
H
h
Pmax
Pmin.
R
Computation of pressure below toe

28. Design of Retaining Walls
Let the resultant R due to W and Pa
lie at a distance x from the toe.
X = M/W,
M = sum of all moments about toe.
Eccentricity of the load = e = (b/2-x)  b/6
Minimum pressure at heel= >Zero.
For zero pressure, e=b/6, resultant should cut the base within the
middle third.
Maximum pressure at toe=  SBC of soil.









b
e
b
W 6
1
Pmin









b
e
b
W 6
1
Pmax
Computation of pressure below toe …contd

29. Design of Retaining Walls
Depth of Foundation
Rankine’s formula:
Df =
=
2
sin
1
sin
1











SBC
2
a
k
γ
SBC
Df

30. Design of Retaining Walls
Stem: Top width 200 mm to 400 mm
Base slab width b= 0.4H to 0.6H, 0.6H
to 0.75H for surcharged wall
Base slab thickness= H/10 to H/14
Toe projection= (1/3-1/4) Base width
Preliminary proportioning of Cantilever Wall
H
200
b= 0.4H to 0.6H
tp= (1/3-1/4)b
H/10 –
H/14

31. Design of Retaining Walls
Behaviour or structural action and design of stem, heel and toe slabs are same as that
of any cantilever slab.
Structural action of Cantilever Retaining Wall

32. Design of Retaining Walls
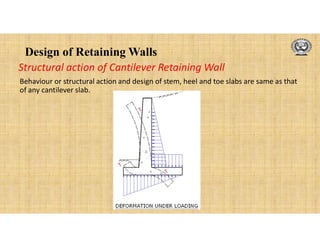
Stem, toe and heel acts as cantilever slabs
Stem design: Mu=psf (ka  H3/6)
Determine the depth d from Mu = Mu, lim=Qbd2
Design as balanced section or URS and find steel
Mu=0.87 fy Ast[d-fyAst/(fckb)]
Design of Cantilever Retaining Wall

33. Design of Retaining Walls
Ast
Provided
Ast/2
Ast
Dist.
from
top
h2
Every
alternate
bar cut
Ast
Ast/2 h2
Ldt
h1c
h1
Effective depth (d) is
Proportional to h
Bending moment is
proportional to h3
Ast is αl to (BM/d) and is
αl to h2
Cross section Curtailment curve
2
2
2
1
2
1
.
.
h
h
A
A
e
i
st
st

Curtailment of Reinforcement

34. Design of Retaining Walls
1. Heel slab and toe slab should also be designed as cantilever.
For this stability analysis should be performed as explained
and determine the maximum bending moments at the
junction.
2. Determine the reinforcement.
3. Also check for shear at the junction.
4. Provide enough development length.
5. Provide the distribution steel
Design of heel and toe slab

35. Design of Retaining Walls
DRAINAGE OF THE BACK FILL

36. Design of Retaining Walls
Sand + Stone Filter
Weepers
Or
Weep Holes

37. Design of Retaining Walls
Drainage Pipes f 100-200 mm @ 2.5 to 4 m

38. Design of Retaining Walls
Perforated Pipe
Suited for short walls