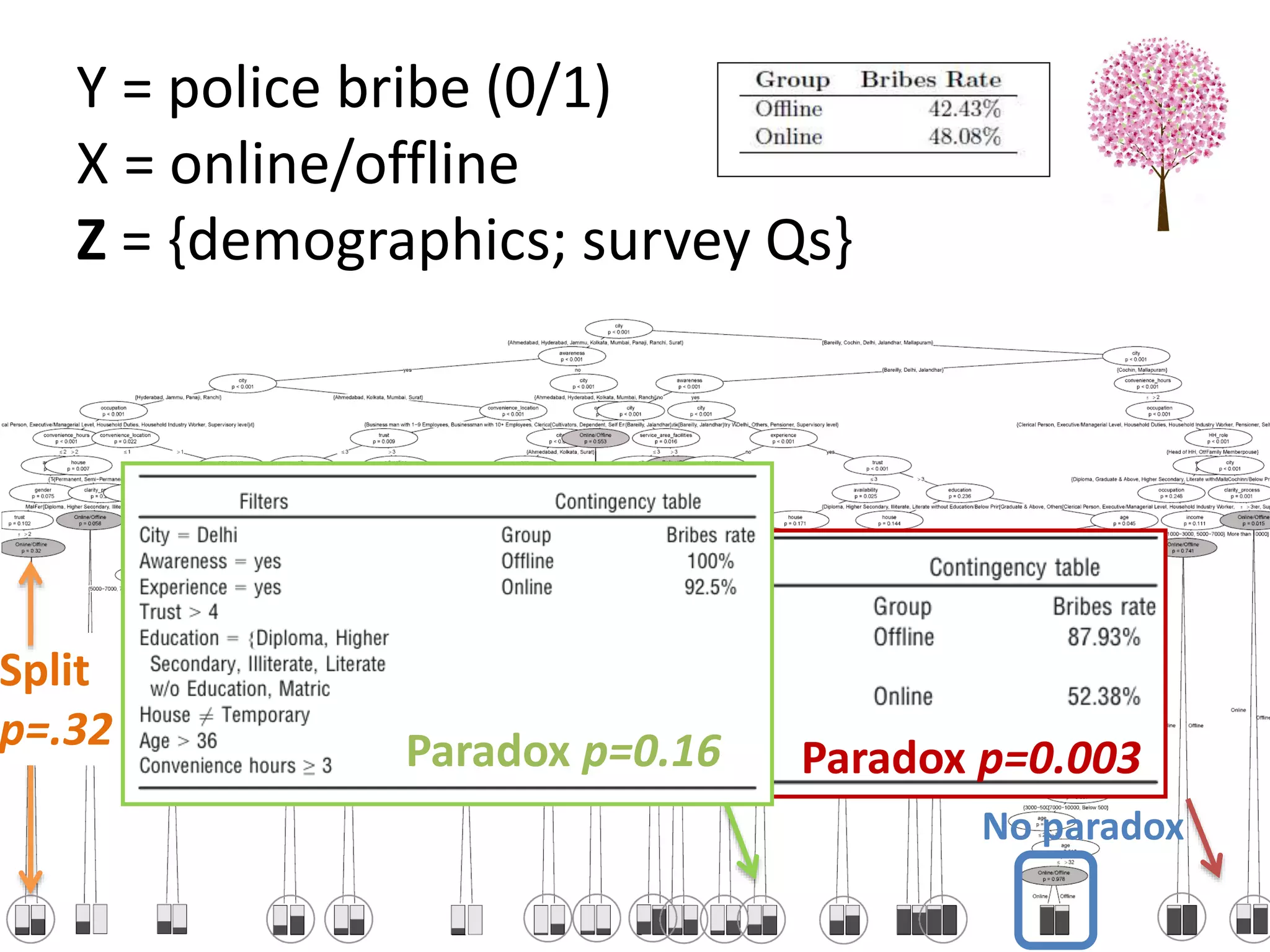
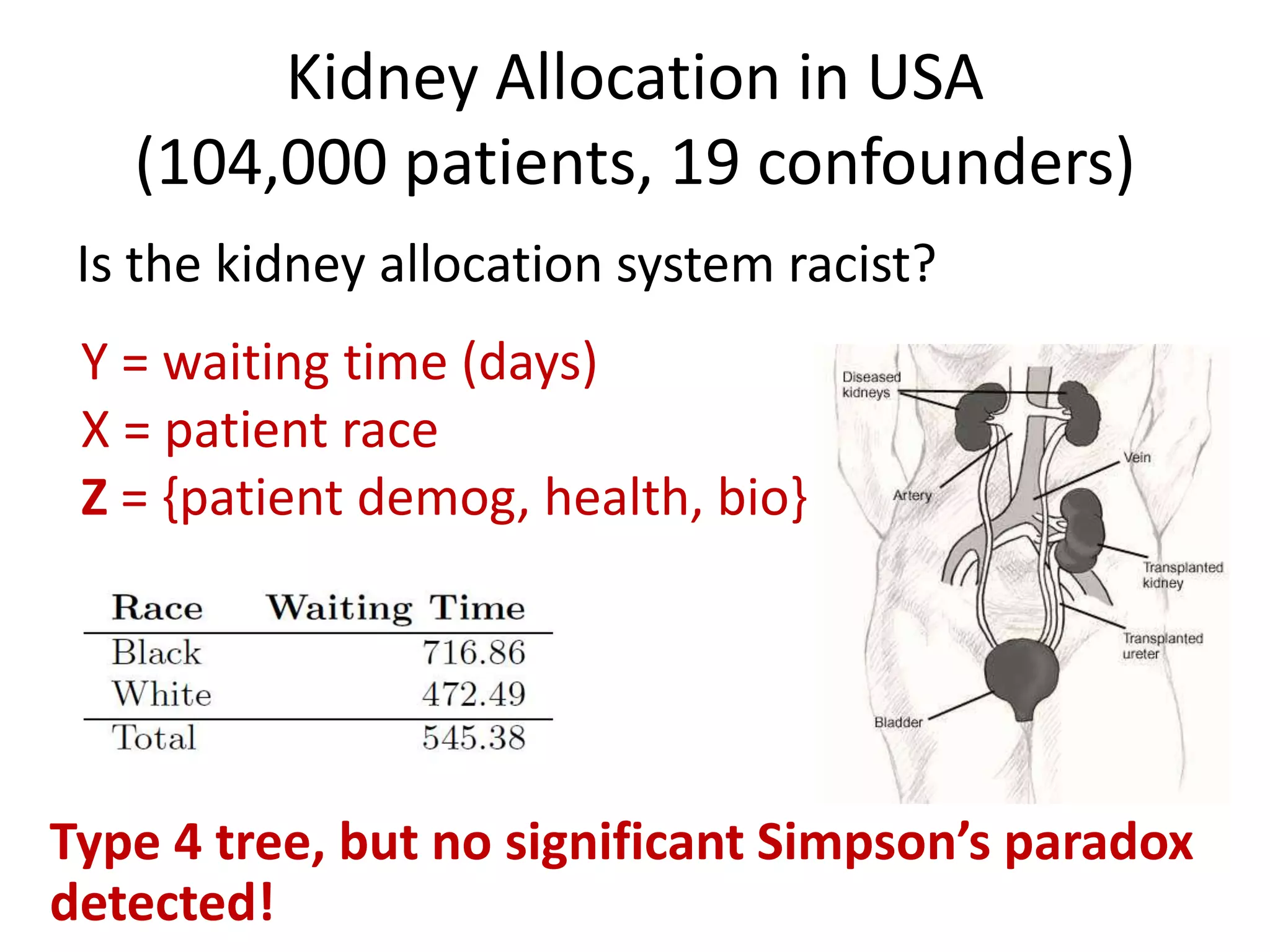
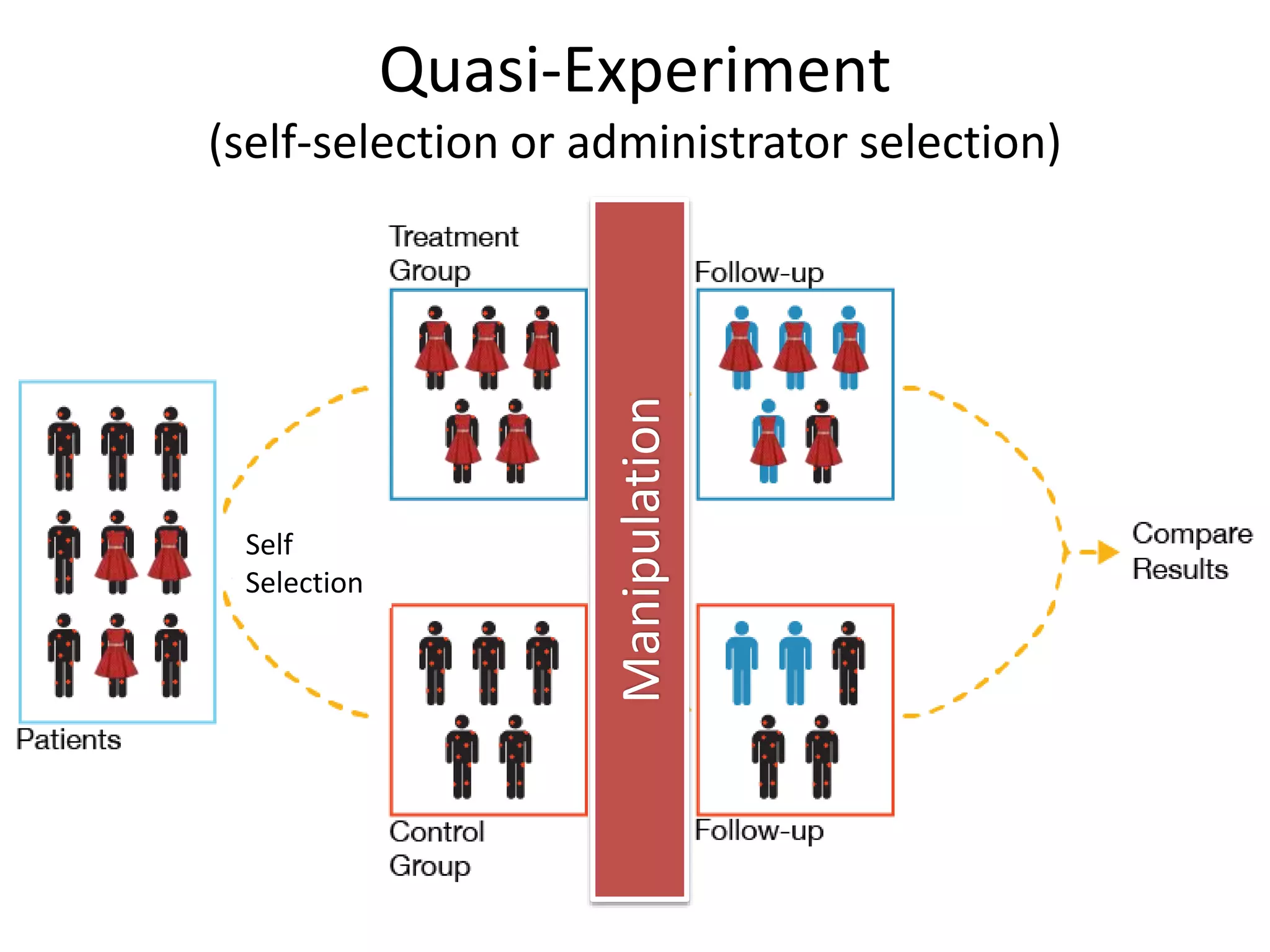
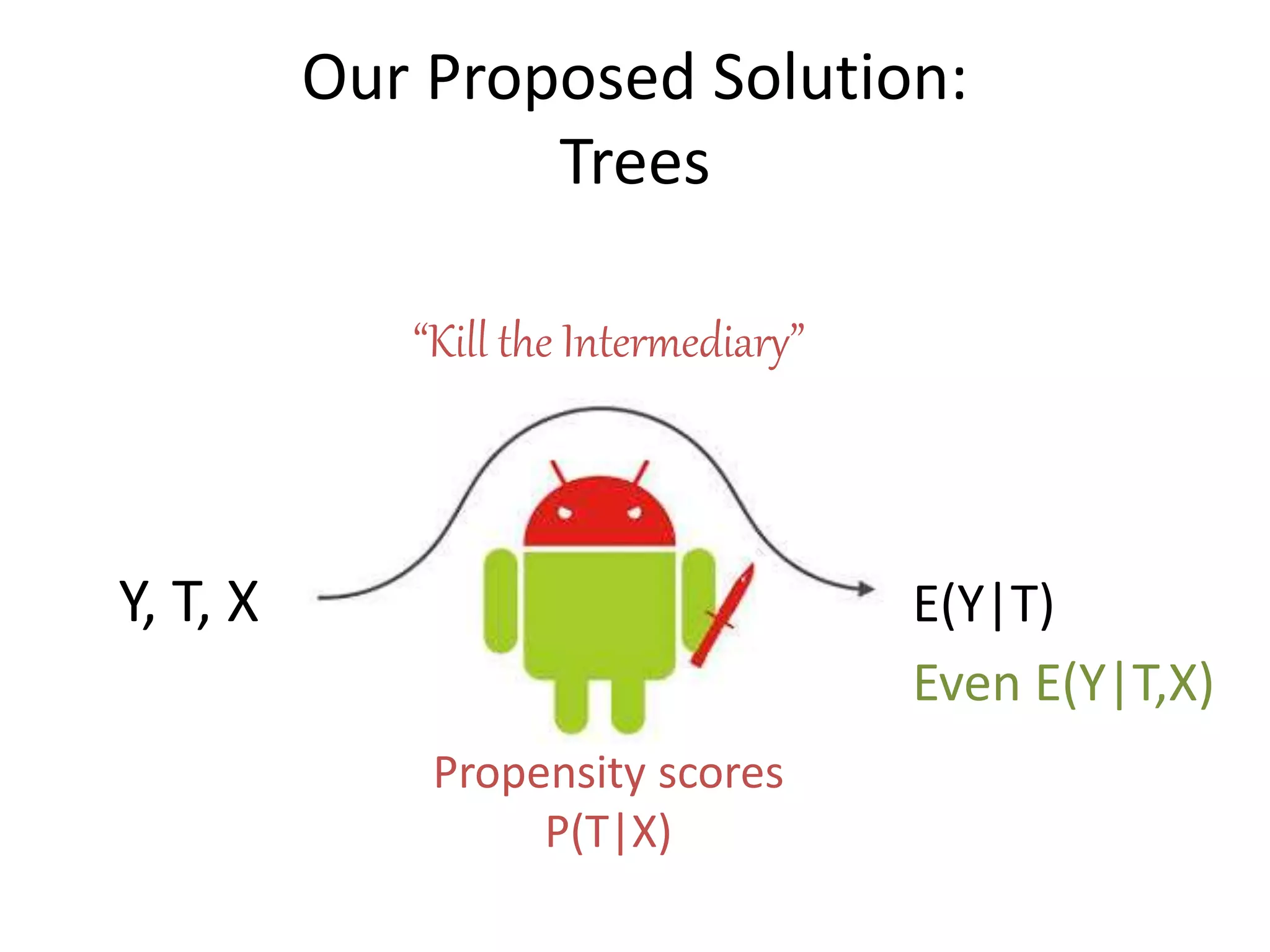
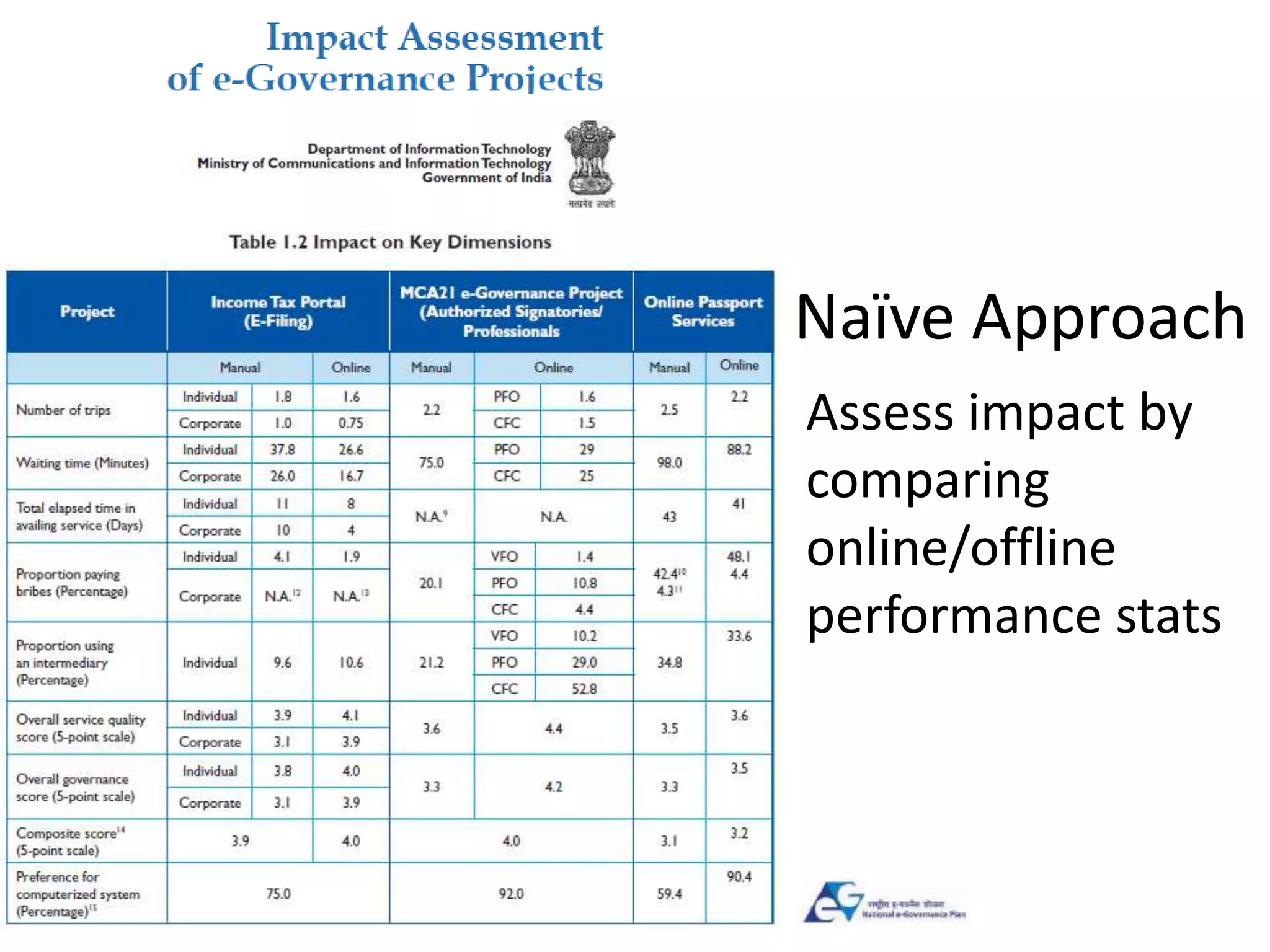
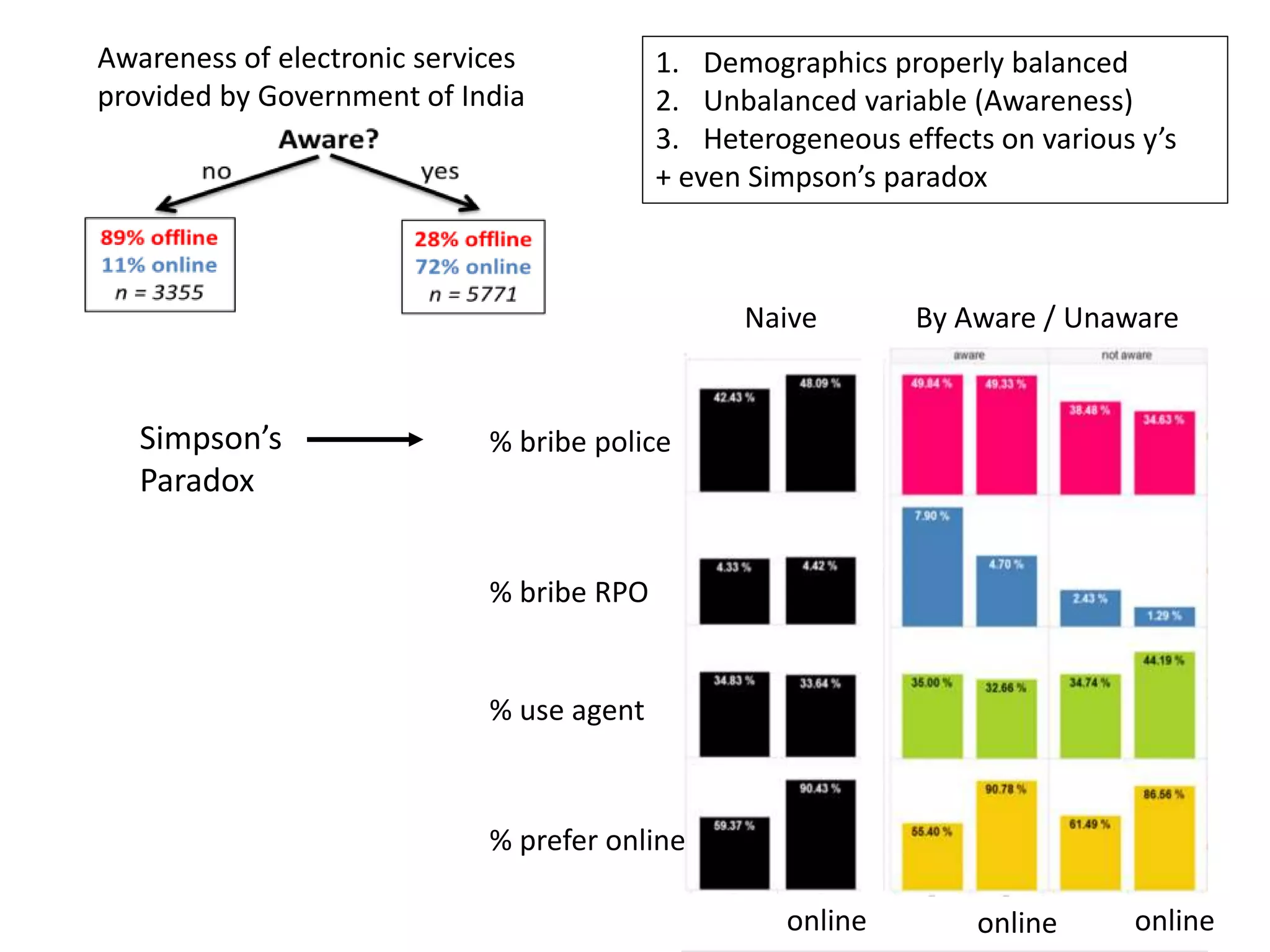
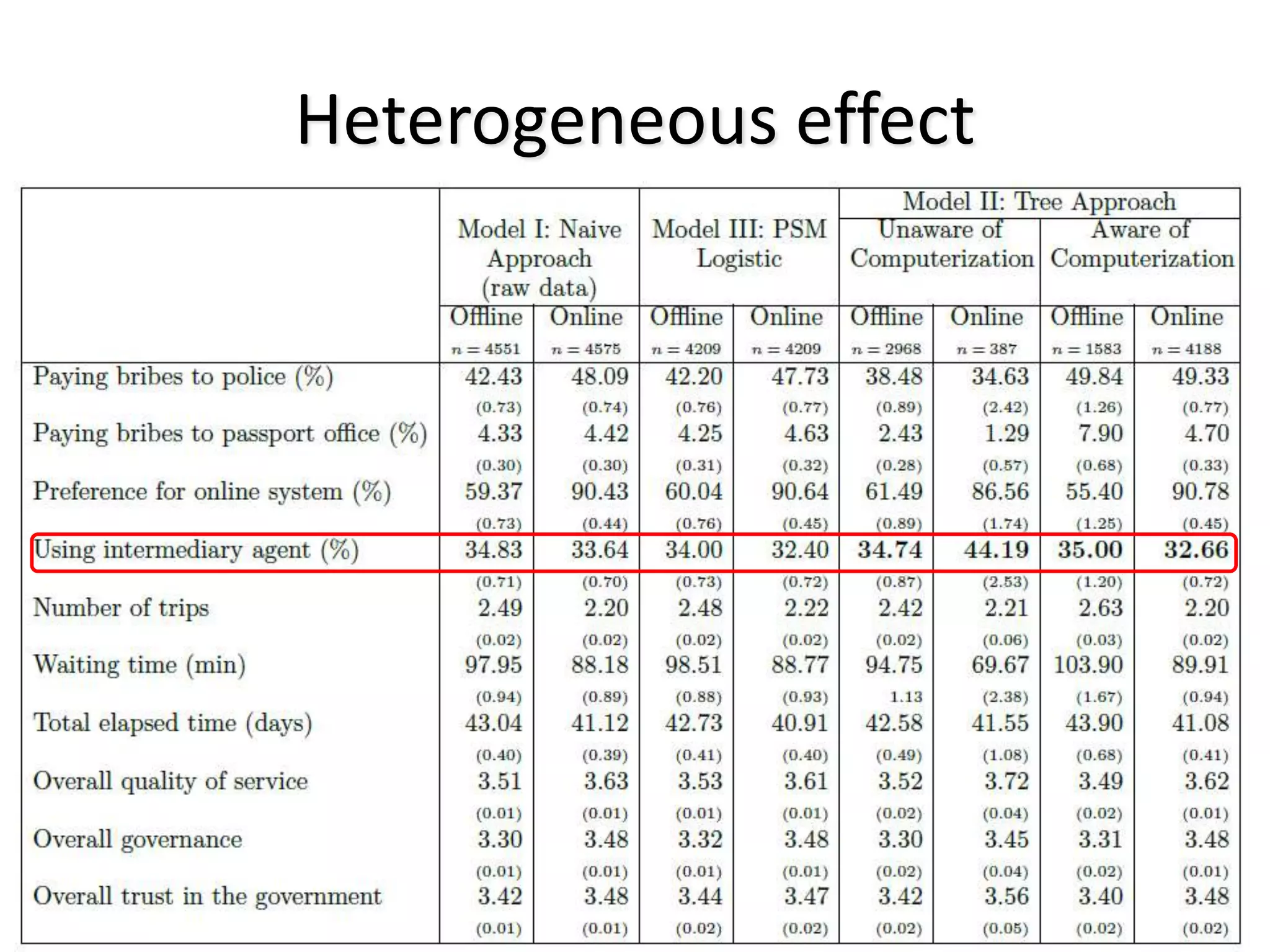
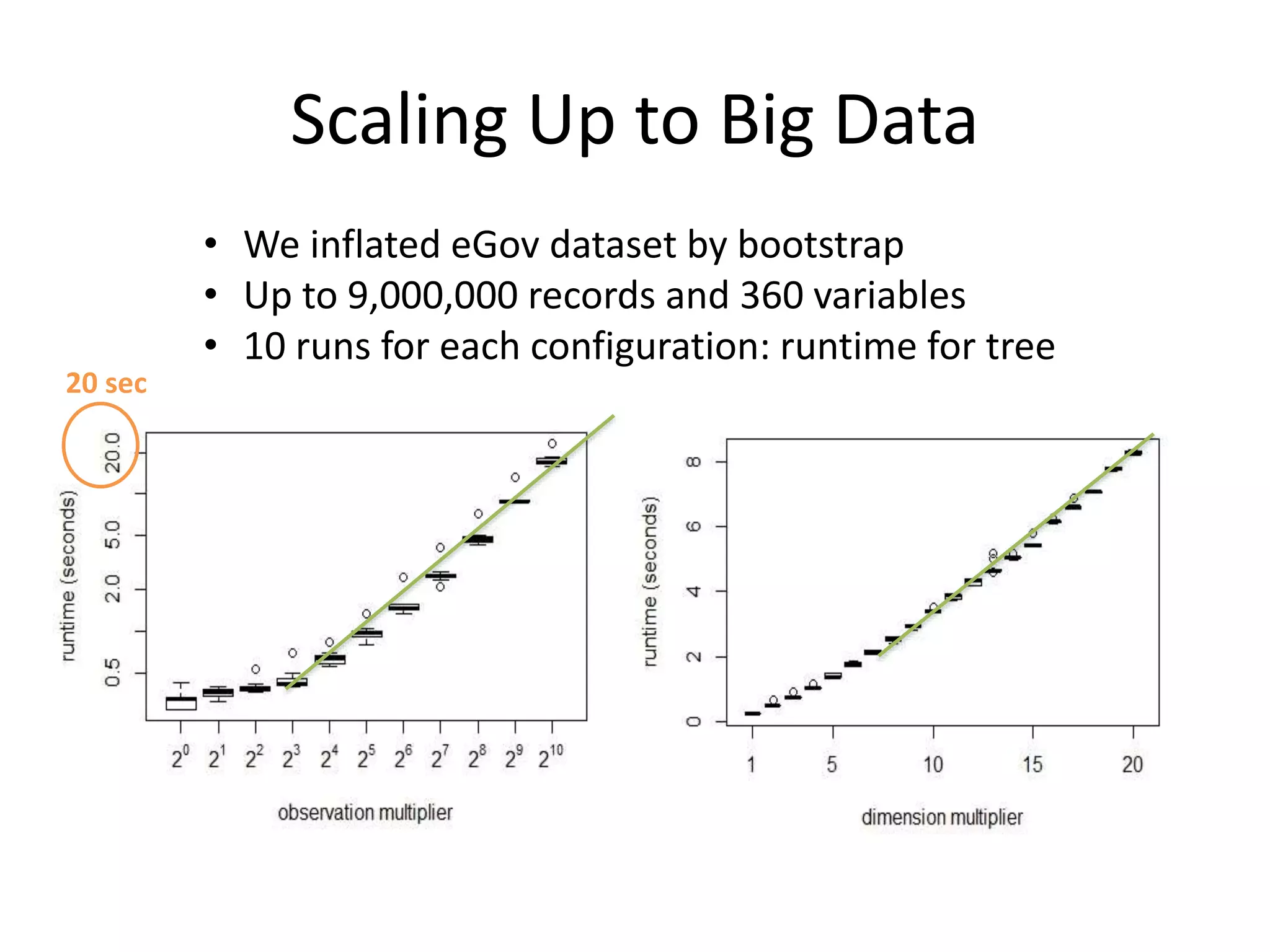
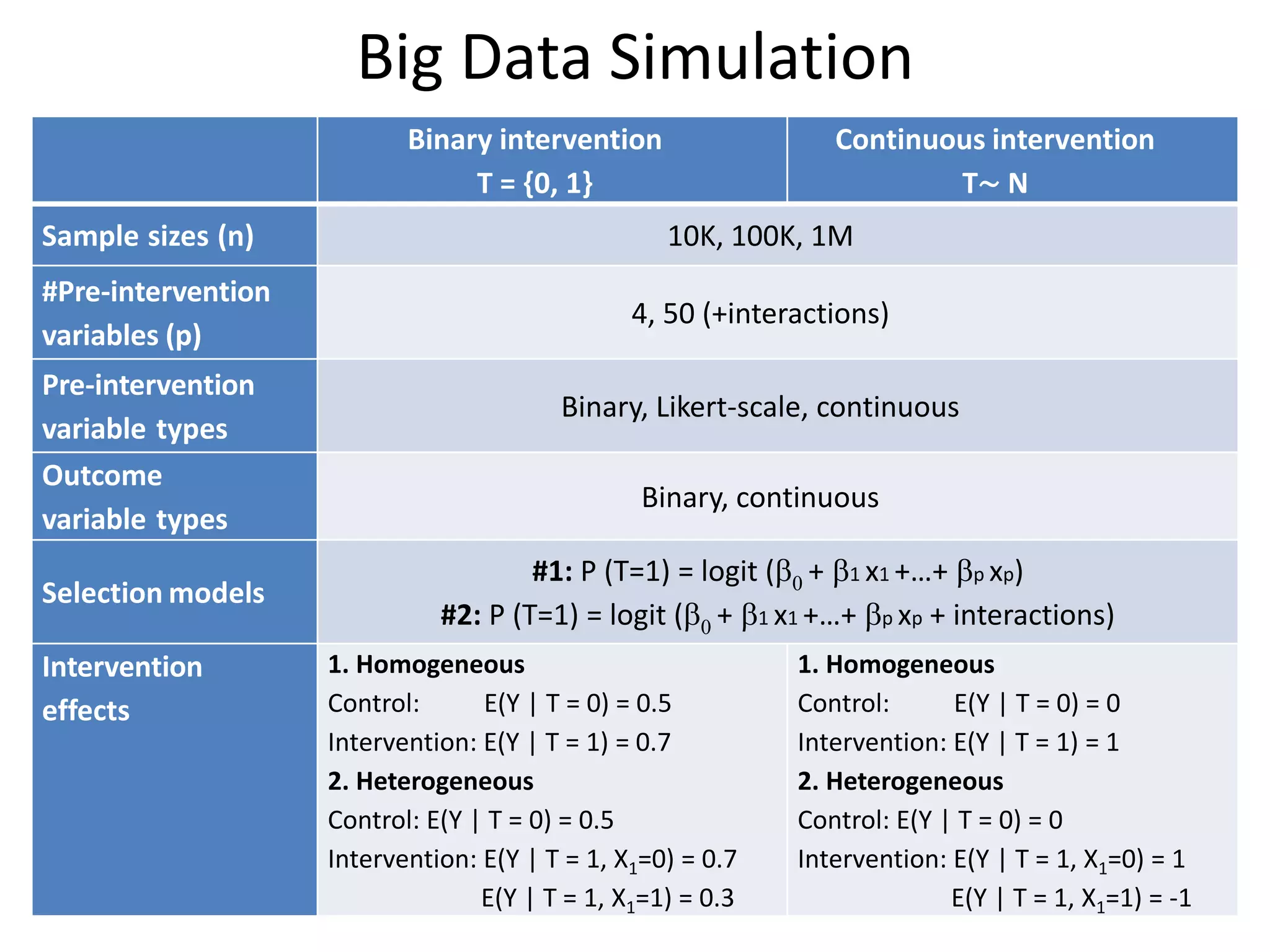
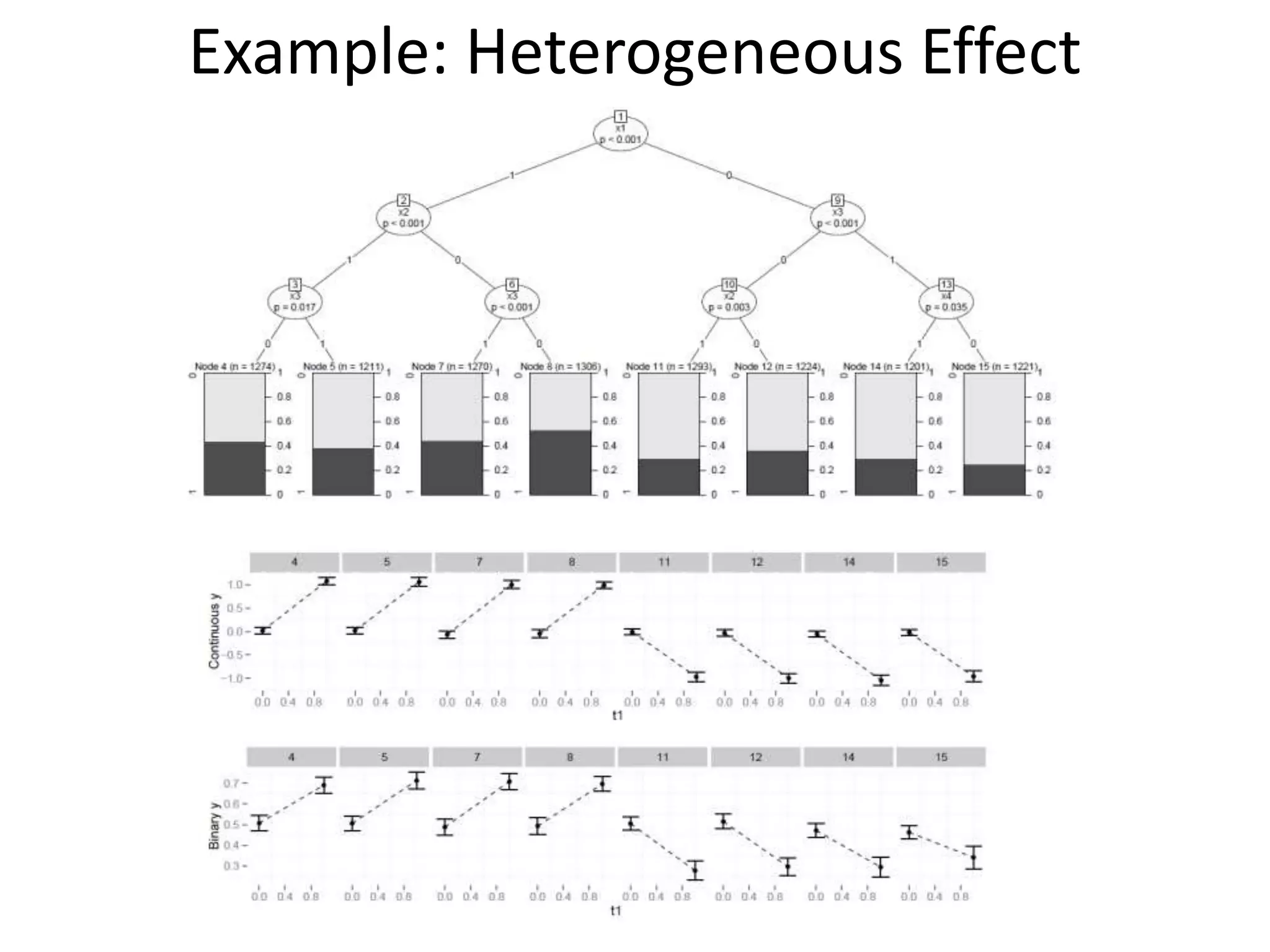
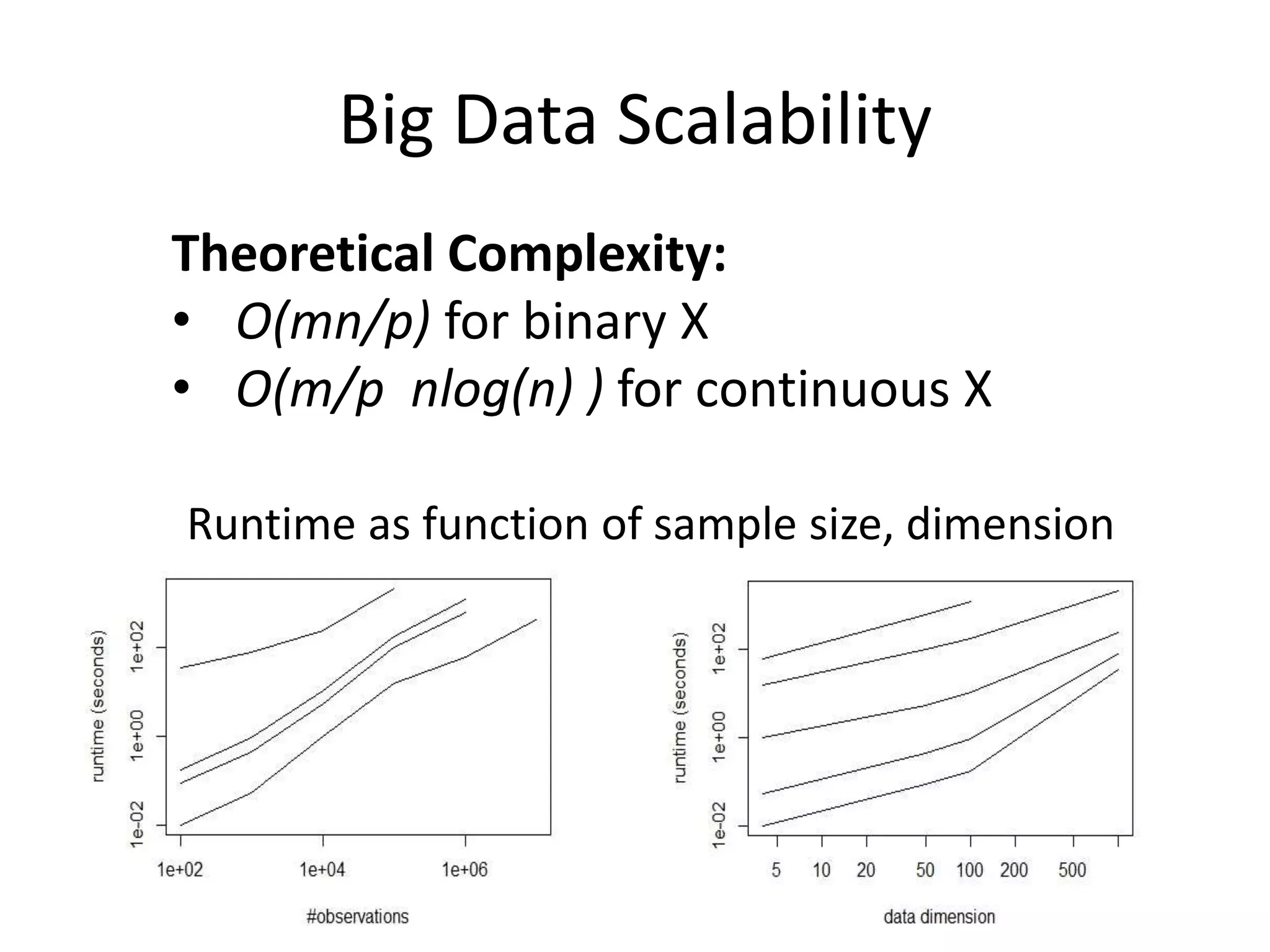
The document discusses a tree-based approach for addressing self-selection in causal research involving high-dimensional data, aimed at improving impact studies such as randomized experiments and quasi-experiments. It outlines the challenges of traditional propensity score methods in big data and proposes a new method that leverages classification and regression trees to identify confounders and analyze treatment effects more effectively. The authors present applications of this method in various domains, demonstrating its advantages over conventional techniques in detecting heterogeneous treatment effects and handling unbalanced covariates.

1. Repurposing Classification & Regression Trees
for Causal Research with High-Dimensional Data
Galit Shmueli 徐茉莉
Institute of Service Science
WOMBAT 2019
Monash University

2. We tackle 2 key issues in causal research:
Self Selection
Identifying Confounders

3. A Tree-Based Approach
for Addressing Self-Selection
in Impact Studies with Big Data
Yahav, Shmueli & Mani (2016), A Tree-Based Approach for Addressing Self-Selection
in Impact Studies with Big Data, MIS Quarterly, vol 40 no 4, pp. 819-848.
With Inbal Yahav (Tel Aviv U) & Deepa Mani (Indian School of Business)

4. The Challenge in Impact Studies
• Individuals/firms self-select intervention
group/duration (quasi-experiment)
• Even in randomized experiments, some variables
might remain unbalanced in sample
How to identify and adjust for self-selection?

5. Randomized Experiment
Manipulation

6. Quasi-Experiment
(self-selection or administrator selection)
Manipulation
Self
Selection

7. Common Approaches
for Addressing Self-Selection
Two steps:
1. Selection model: T = f(X)
2. Performance analysis on matched samples
Y = performance measure(s)
T = treatment
X = pre-intervention variables
Self-selection:
P(T|X) ≠P(T)
• 2SLS modeling (Heckman correction) -- econometrics
• Propensity Score Approach (PS) -- statistics

8. Propensity Scores Approach
Step 1: Estimate selection model logit(T) = f(X)
to compute propensity scores P(T|X)
Step 3: Estimate Effect (compare matched groups)
e.g., t-test or Y = b0 + b1 T+ b2 X+ b3 PS +e
Step 2: Use scores to create matched samples
PSM = use matching algorithm
PSS = divide scores into bins

9. Challenges of PS in Big Data
1. Matching leads to severe data loss
2. PS methods suffer from “data dredging”
3. No variable selection (what drive selection?)
4. Assumes constant intervention effect
5. Sequential process is computationally costly
6. Logistic model requires specifying exact form
of selection model

10. Our Proposed Solution:
Trees
Propensity scores
P(T|X)
Y, T, X E(Y|T)
Even E(Y|T,X)
“Kill the Intermediary”

11. Proposed Method: Tree
Output: T (treat/control)
Inputs: X’s (income, education, family…)
Records in each terminal node
share same profile (X) and same
propensity score P(T=1|X)

12. Tree-Based Approach
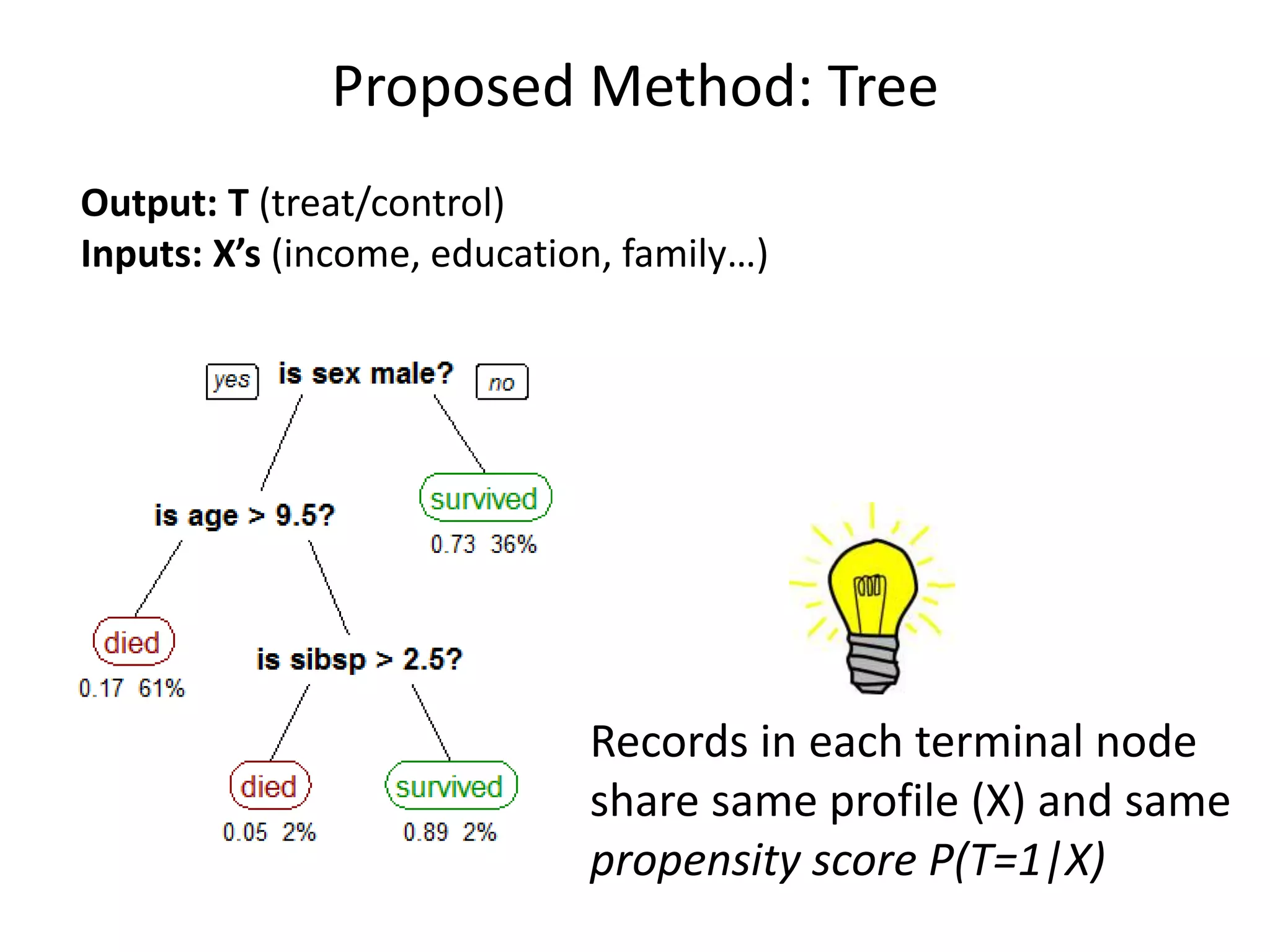
Four steps:
1. Run selection model: fit tree T = f(X)
2. Visualize tree; see unbalanced X’s
3. Treat each terminal node as sub-sample;
conduct terminal-node-level performance
analysis
4. Present terminal-node-analyses visually
5. [optional]: combine analyses from nodes with
homogeneous effects
Like PS, assumes observable self-selection

13. Three Applications (MISQ 2016)
1. Impact of labor training on earnings
(Famous) randomized experiment by US gov
2. Impact of new online passport service on
bribing, efficiency,…
Quasi-experiment by India gov
3. Impact of outsourcing contract pricing &
duration on financial performance

14. Study 1: Impact of training on financial gains
In mid-1970’s US govt program randomly
assigned eligible candidates to labor training
program
• Goal: increase future earnings
• LaLonde (1986) showed:
Groups statistically equal in terms of demographic
& pre-train earnings
 ATE = $1794 (p<0.004)

15. Tree on Lalonde’s RCT data
If groups are completely
balanced, we expect…
Y = Earnings in 1978
T = Received NSW training (T = 1) or not (T = 0)
X = Demographic information and prior earnings

16. Tree reveals…
LaLonde’s naïve approach
(experiment)
Tree approach
HS dropout
(n=348)
HS degree
(n=97)
Not trained (n=260) $4554 $4,495 $4,855
Trained (n=185) $6349 $5,649 $8,047
Training effect
$1794
(p=0.004)
$1,154
(p=0.063)
$3,192
(p=0.015)
Overall: $1598
(p=0.017)
no yes
High school
degree
1. Unbalanced variable (HS degree)
2. Heterogeneous effect

17. Labor Training effect:
Observational control group
• LaLonde also compared with observational
control groups (PSID, CPS)
– experimental training group vs. obs control
– showed training effect not estimated correctly with
structural equations
• Dehejia & Wahba (1999,2002) re-analyzed CPS
control group (n=15,991), using PSM
– Effects in range [$1122, $1681], depends on settings
– “Best” setting effect: $1360
– Uses only 119 control group members (out of 15,991)

18. Tree for obs control group reveals…
unemployed prior to training
in 1974 (u74=0 )
-> negative effect outlier
eligibility
issue!
some profiles are rare in
trained group but
popular in control group
1. Unbalanced variables
2. Heterogeneous effect in u74
3. Outlier
4. Eligibility issue

19. Study 2:
Impact of eGov Initiative
(India)
Survey commissioned by Govt of India in 2006
• >9500 individuals who used passport services
• Representative sample of 13 Passport Offices
• “Quasi-experimental, non-equivalent groups design”
• Equal number of offline and online users, matched by
geography and demographics

20. Naïve Approach
Assess impact by
comparing
online/offline
performance stats

21. % bribe RPO
% use agent
% prefer online
% bribe police
Naive By Aware / Unaware
online onlineonline
Awareness of electronic services
provided by Government of India
Simpson’s
Paradox
1. Demographics properly balanced
2. Unbalanced variable (Awareness)
3. Heterogeneous effects on various y’s
+ even Simpson’s paradox

22. PSMAwareness of electronic services
provided by Government of India
Would we detect this
with PSM?

23. Heterogeneous effect

24. Scaling Up to Big Data
• We inflated eGov dataset by bootstrap
• Up to 9,000,000 records and 360 variables
• 10 runs for each configuration: runtime for tree
20 sec

25. Big Data Simulation
Binary intervention
T = {0, 1}
Continuous intervention
T∼ N
Sample sizes (n) 10K, 100K, 1M
#Pre-intervention
variables (p)
4, 50 (+interactions)
Pre-intervention
variable types
Binary, Likert-scale, continuous
Outcome
variable types
Binary, continuous
Selection models
#1: P (T=1) = logit (b0 + b1 x1 +…+ bp xp)
#2: P (T=1) = logit (b0 + b1 x1 +…+ bp xp + interactions)
Intervention
effects
1. Homogeneous
Control: E(Y | T = 0) = 0.5
Intervention: E(Y | T = 1) = 0.7
2. Heterogeneous
Control: E(Y | T = 0) = 0.5
Intervention: E(Y | T = 1, X1=0) = 0.7
E(Y | T = 1, X1=1) = 0.3
1. Homogeneous
Control: E(Y | T = 0) = 0
Intervention: E(Y | T = 1) = 1
2. Heterogeneous
Control: E(Y | T = 0) = 0
Intervention: E(Y | T = 1, X1=0) = 1
E(Y | T = 1, X1=1) = -1

26. Example: Heterogeneous Effect

27. Big Data Scalability
Theoretical Complexity:
• O(mn/p) for binary X
• O(m/p nlog(n) ) for continuous X
Runtime as function of sample size, dimension

28. Scaling Trees Even Further
• “Big Data” in research vs. industry
• Industrial scaling
– Sequential trees: efficient data structure, access
(SPRINT, SLIQ, RainForest)
– Parallel computing (parallel SPRINT, ScalParC,
SPARK, PLANET) “as long as split metric can be
computed on subsets of the training data and
later aggregated, PLANET can be easily extended”

29. Tree Approach Benefits
1. Data-driven selection model
2. Scales up to Big Data
3. Less user choices (data dredging)
4. Nuanced insights
• Detect unbalanced variables
• Detect heterogeneous effect from anticipated outcomes
5. Simple to communicate
6. Automatic variable selection
7. Missing values do not remove record
8. Binary, multiple, continuous interventions
9. Post-analysis of RCT quasi-experiments & observational studies

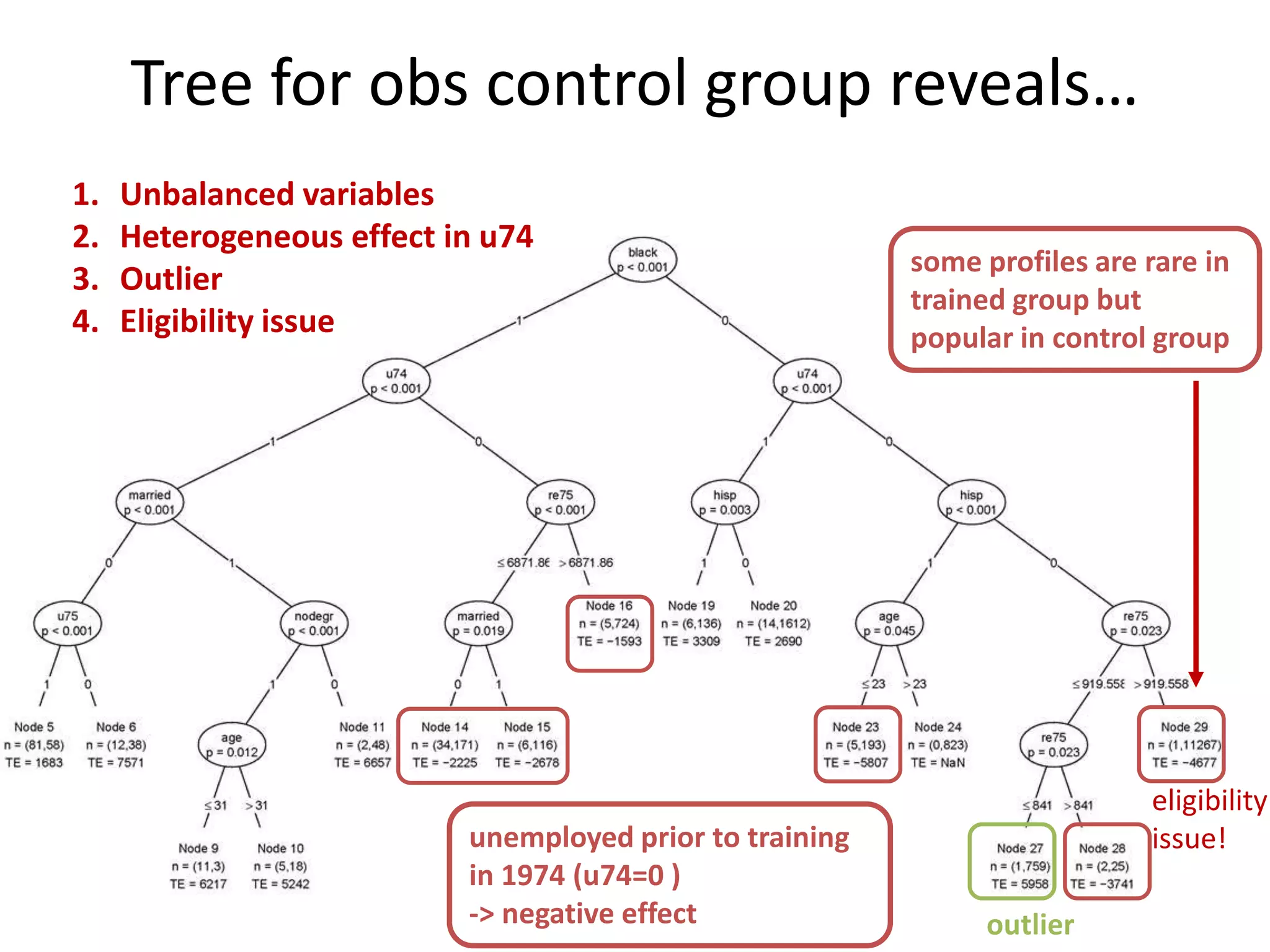
30. Tree Approach Limits
1. Assumes selection on observables
2. Need sufficient data
3. Continuous variables can lead to large tree
4. Instability
[possible solution: use variable importance scores (forest)]

31. Detecting
Simpson’s Paradox
in Big Data
Using Trees
Shmueli & Yahav (2017), The Forest or the Trees? Tackling Simpson’s Paradox with
Classification Trees, Production & Operations Management Journal, Forthcoming
With Inbal Yahav, Tel Aviv University

32. Simpson’s Paradox
The direction of a cause on an effect appears reversed when
examining aggregate vs. disaggregate of a sample (or population)
Simpson's Paradox is the reversal
of an association between two
variables after a third variable is
taken into account
Schield (1999)
The phenomenon whereby an event B
increases the probability of A in a given
population p, at the same time, decreases the
probability of A in every subpopulation of p.
Pearl (2009)

33. Death Sentence and Race
(Agresti, 1984)
Does defendant's race (X) affect
chance of death sentence (Y)?
Causal explanation:
Black murderers tend to kill blacks;
hence lower overall death sentence rates
Causal effect seems
to reverse when
disaggregating by
victim race (Z)

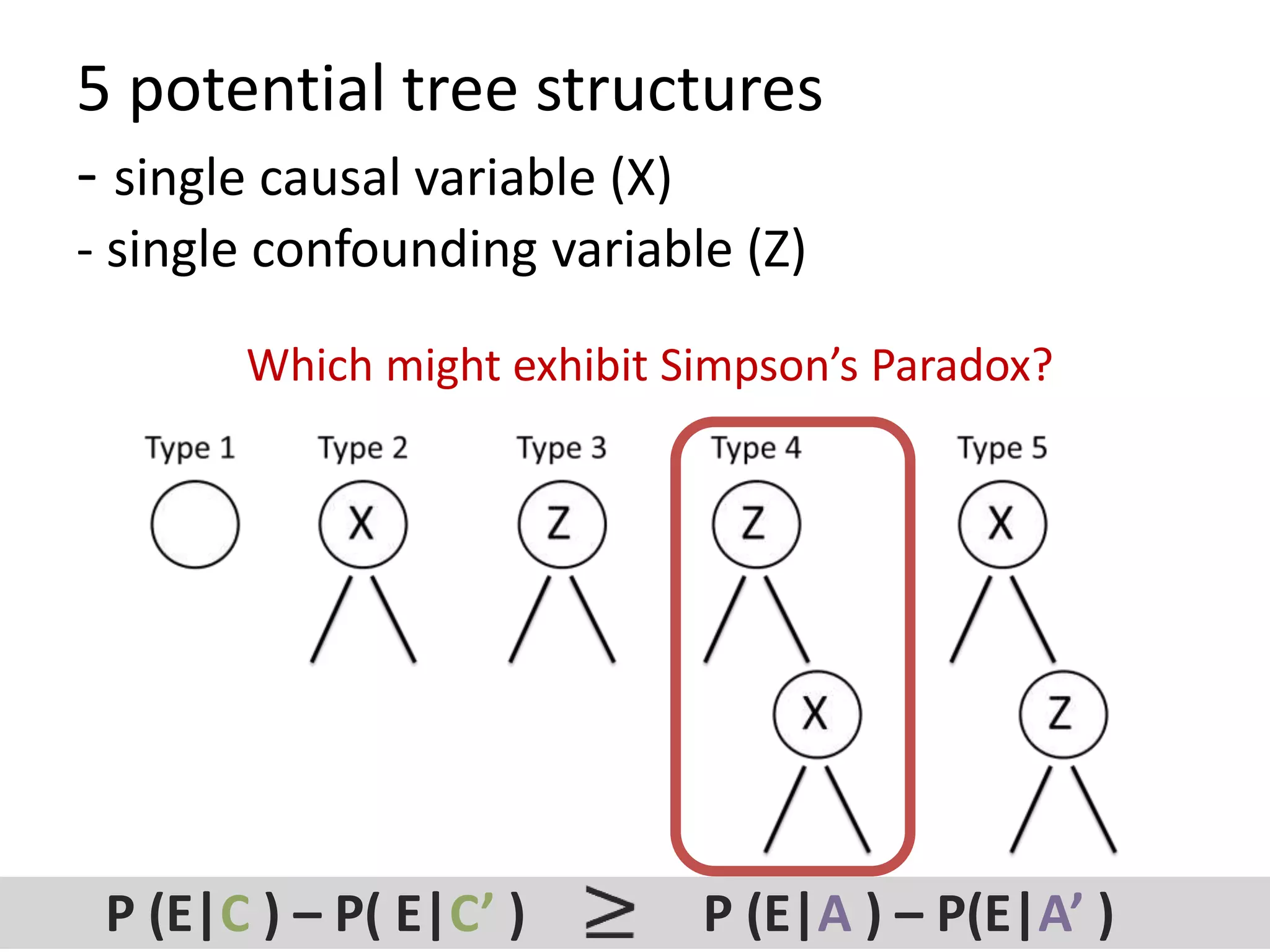
34. Goal: Does a dataset exhibit SP?
C = confounder
E = effectA = cause
P (E|C ) – P( E|C’ ) P (E|A ) – P(E|A’ )
“If Cornfield’s minimum effect size is not reached,
[you] can assume no causality” Schield, 1999
Cornfield et al’s Criterion

35. Translate Cornfield’s Criterion
into a Tree
Y = outcome of interest
X = causal variable
Z = confounding variable(s)
Tree Predictors
#1
If cause -> effect, then
cause should appear in tree
#2
If Z is confounder, then
Z should appear in tree

36. 5 potential tree structures
- single causal variable (X)
- single confounding variable (Z)
Which might exhibit Simpson’s Paradox?
P (E|C ) – P( E|C’ ) P (E|A ) – P(E|A’ )

37. Simpson’s Paradox on a Tree
#1
If cause -> effect, then cause
should appear in tree
#2
If Z is confounder, then
Z should appear in tree
#3
Z should appear before cause
(Cornfield criterion)

38. Death Sentence and Race:
Tree Approach #1: full tree
P(death)

39. Accounting for Sampling Error
Logistic/linear regression:
Interaction X*Z significant?
No → no paradox
Yes → ?
Trees:
Tree structure + significance of interaction
= conditional-inference tree
Tree splits based on statistical tests
(c2, F , permutation tests)

40. Tree Approach #2:
Conditional Inference tree
(Hothorn et al., JCGS 2006)
Variable selection based on statistical test (c2)
• Recursive partitioning with early stopping
• Separate steps for variable selection and split search
• R packages party, partykit (function ctree)

41. Cornfield’s criterion + sampling error:
Conditional Inference Trees

42. Proof for trees that use concave impurity
measure (Gini, entropy) as well as c2
CART, CHAID, Conditional-Inference Trees

43. Accounting for Sampling Error:
Conditional-Inference Tree
P(death)

44. Seatbelts and Injuries (Agresti 2012)
Does use of seat-belts (X) reduce chance of injury (Y)?
Z = Passenger gender and accident location
n=68,694 passengers involved in accidents in Maine
Potential Paradox
(by location)
How about logistic regression?

45. % Injuries

46. Simpson’s Paradox in Big Data
Large n , High-dimensional Z

47. Multiple Potential Confounders (Z)
The Challenge
Statistical significance of
Simpson’s paradox
≠
Significance threshold of
tree splits in CI treeCI Tree Full Tree
Solution: X-Terminal Tree

48. Paradox Detection in Big Data
(Tree Approach #3):
X-Terminal Trees
X-Terminal Tree:
Grow tree only
until X-splits

49. Tree paths with terminal X nodes
can indicate…
• Full paradox, statistically significant
• Partial paradox, statistically significant
• Statistically insignificant paradox
• No paradox
Pivot table equivalence:
Filter by Z variables above terminal X node

50. Impact of eGov Initiative
(India)
Survey commissioned by Govt of India in 2006
• >9500 individuals who used passport services
• Representative sample of 13 Passport Offices
• “Quasi-experimental, non-equivalent groups design”
• Equal number of offline and online users, matched by
geography and demographics

51. Y = police bribe (0/1)
X = online/offline
Z = {demographics; survey Qs}
Split
p=.32
Paradox p=0.003Paradox p=0.16
No paradox

52. Kidney Allocation in USA
(104,000 patients, 19 confounders)
Is the kidney allocation system racist?
Type 4 tree, but no significant Simpson’s paradox
detected!
Y = waiting time (days)
X = patient race
Z = {patient demog, health, bio}

53. • Greediness of tree
• Weak paradox or in
small subset of data
can go undetected
• Highly correlated Z’s
might lead to
“wrong” Z choice
Summary & Challenges
Full tree: eliminate non-type-4 trees
Conditional-inference trees: for single Z
X-terminal trees: for multiple Zs
• More efficient than
stepwise regression
• Tree structure more
informative than
interaction terms
• Extends: continuous Y,
>2 subpopulations

54. We tackle 2 key issues in causal research:
Self Selection
Identifying Confounders

55. Anal yt ics
Humanit y
Responsibil it y
Galit Shmueli 徐茉莉
Institute of Service Science